s3ankrau1
Aus ProgrammingWiki
Inhaltsverzeichnis |
Übungsaufgaben
Vorlesung 1
Wiederholen Sie die Eigenschaften von Äquivalenzrelationen und geben Sie ein Beispiel an.
- Reflexivität: $a\sim a$
Jedes Objekt ist zu sich selbst äquivalent.
- Symmetrie: $a\sim b \ \Rightarrow\ b\sim a$
Wenn $a$ zu $b$ äquivalent ist, dann ist auch $b$ äquivalent zu $a$ (und umgekehrt).
- Transitivität: $a\sim b\ \mathrm{und}\ b\sim c\ \Rightarrow\ a\sim c$
Wenn $a$ zu $b$ äquivalent und $b$ zu $c$ äquivalent ist, dann ist $a$ äquivalent zu $c$.
Beispiel: Ein Beispiel aus der Landwirtschaft soll die eingeführten Begriffe verdeutlichen. Betrachtet sei eine Menge $M$ von Nutztieren in einem landwirtschaftlichen Betrieb. Wir definieren die folgende zweistellige Relation $\sim$ auf $M$:
Für je zwei Nutztiere $x$ und $y$ aus $M$ soll $x\sim y$ genau dann gelten, wenn $x$ und $y$ Tiere derselben Art sind. Für die Kuh $K$ und den Ochsen $O$ gilt $K\sim O$. Für das Huhn $H$ gilt aber nicht $H\sim K$. Die Relation $\sim$ erfüllt die drei Forderungen für Äquivalenzrelationen:
- Reflexivität
Jedes Tier ist von derselben Art wie es selbst.
- Symmetrie
Ist ein Tier von derselben Art wie ein zweites, dann ist das zweite auch von derselben Art wie das erste.
- Transitivität
Wenn $K$ und $O$ Tiere derselben Art sind und ebenso $O$ und $L$ von derselben Art sind, dann sind auch $K$ und $L$ von derselben Art (nämlich von der Art, zu der dann jedes der drei Tiere gehört).
Schreiben Sie ein Programm, das q berechnet.
Die im Folg. definierte Funktion $q : \R \mapsto \R$ ist an der Stelle $x=3$ undefiniert. Hierfür verwenden wir das Symbol $\bot$.
$$q(x)=\begin{cases} \dfrac{35}{x-3}, & \text{wenn }x \neq 3\text{;}\\ \bot, & \text{sonst.} \end{cases} $$
Geben Sie sich einige Definitionsbeispiele selbstgewählter Funktionen vor. Achten Sie darauf, dass es sich auch um (echte) partielle Funktionen handeln kann. Außerdem sollten Sie einige abschnittsweise definierte Funktionen, z.B. Briefporto, Zuzahlungen für Medikamente usw., aufnehmen.
Funktion für die Berechnung des Portos von Briefen anhand des Gewichts $x$ in Gramm:
$$p(x)=\begin{cases} 0.62, & \text{wenn }0 < x \leq 20\text{;}\\ 0.85, & \text{wenn }20 < x \leq 50\text{;}\\ 1.45, & \text{wenn }50 < x \leq 500\text{;}\\ 2.40, & \text{sonst.} \end{cases} $$
Wiederholen Sie die folgenden Eigenschaften von Funktionen: injektiv, surjektiv und bijektiv. Geben Sie aussagekräftige Beispiele an. Skizzieren Sie folgende Funktionen mittels Abbildungspfeilen aus X in Y : injektiv und surjektiv; injektiv, nicht surjektiv; nicht injektiv, surjektiv; nicht injektiv, nicht surjektiv.
| Eigenschaft | Beschreibung | Beispiele |
|---|---|---|
| injektiv | Jedes Element aus Y hat höchstens einen Partner in X | $ \N \Rightarrow \N, x \rightarrow x^2 $ |
| surjektiv | Jedes Element aus Y hat mindestens einen Partner in X | $ \R \Rightarrow \R_{+}, x \rightarrow x^2 $ |
| bijektiv | Jedes Element aus Y hat genau einen Partner in X (muss injektiv und surjektiv sein) | $ \R_{+} \Rightarrow \R_{+}, x \rightarrow x^2 $ |
| Funktion $X \Rightarrow Y$ | Darstellung |
|---|---|
| injektiv,surjektiv | 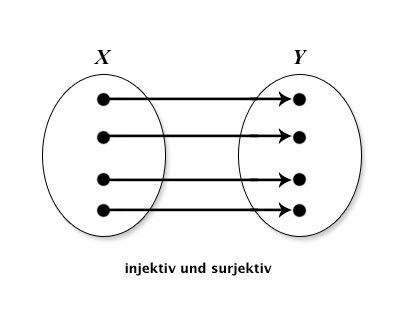
|
| injektiv,nicht surjektiv | 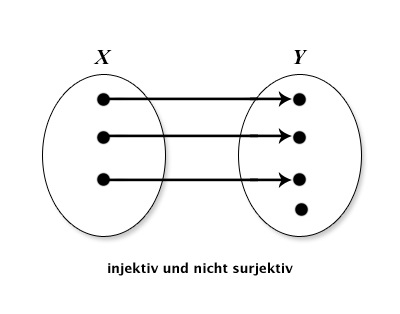
|
| nicht injektiv,surjektiv | 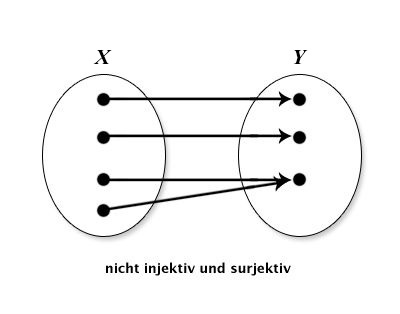
|
| nicht injektiv,nicht surjektiv | 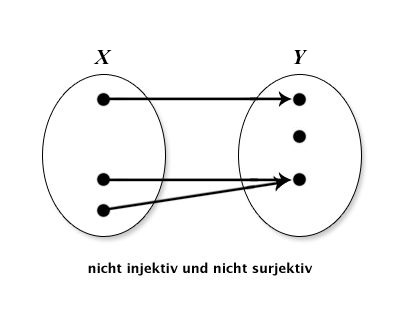
|
Zeigen Sie, dass die Menge $\Z$ eine abzählbar unendliche Menge ist und setzen Sie sich mit der Aussage auseinander, wonach doch $\Z$ eigentlich doppelt so viele Elemente besitzt, wie $\N$.
Eine abzählbar unendliche Menge ist dadurch definiert, dass sie die selbe Mächtigkeit wie die Menge der natürlichen Zahlen hat. Man kann also jedes Element der Menge auf ein Element der natürlichen Zahlen abbilden. Man definiert $f : \Z \to \N$:
$$f(z)=\begin{cases} −(2z+1), & \text{wenn }z < 0 \text{;}\\ 2z, & \text{wenn } z \geq 0 \end{cases} $$
Entwerfen Sie ein Aufbauschema zur systematischen Erzeugung aller Elemente aus ℘(M) für eine gegebene endliche Menge M und wenden Sie es auf einige selbstgewählte Beispiele an.
- Leere Menge aufnehmen
- Nimm ein Element aus der Menge und füge es jedem Element der vorher gebildeten Menge Hinzu und übernimm die vorher gebildetetn Elemente
Beispiel für $ \wp(\{a,b,c\}) $
$ \wp(\{\})=\{\{\emptyset\}\} $
$ \wp(\{c\})=\{\{\emptyset\},\{c\}\} $
$ \wp(\{b,c\})=\{\{\emptyset\},\{c\},\{b\},\{b,c\}\} $
$ \wp(\{a,b,c\})=\{\{\emptyset\},\{c\},\{b\},\{b,c\},\{a\},\{a,b\},\{a,c\},\{a,b,c\}\} $
Vorlesung 2
Kommentieren Sie. Nennen Sie Beispiele.
- Unzugängliches (wenigstens) für Computer
- Keine Beschreibungssprache vorhanden, daher nicht formalisierbar/maschinell beschreibbar
- Probleme zu vielschichtig und mit mehreren abhängigen Parametern
- Beispiel: "Wird es morgen regnen?", "Wer gewinnt das WM-Finale?"
- Praktisch Unmögliches
- Problem zwar maschinell beschreibbar, doch kann es aufgrund von Ressourcen-Problemen praktisch nicht gelöst werden
- Beispiele sind das n-Damen-Problem oder TSM für sehr große Probleminstanzen
Warum ist es so schwierig ein leistungsfähiges Schachprogramm zu entwerfen?
Zeigen Sie, dass die folgenden Mengen abzählbar unendlich sind: $\Z$, $\Q$, die Menge der Primzahlen, die geraden Zahlen.
- Für $\Z$:
| 0 | 1 | 2 | 3 | 4 | 5 | ... |
| 0 | 1 | -1 | 2 | -2 | 3 | ... |
$$f(z)=\begin{cases} −(2z+1), & \text{wenn }z < 0 \text{;}\\ 2z, & \text{wenn } z \geq 0 \end{cases} $$
- Für $\Q$:
$\Q=\{\frac{a}{b} | a \in \Z, b\in \N\}$
Beweis mit Cantors erstem Diagonalargument:
| $b$\$a$ | $0$ | $1$ | $-1$ | $2$ | $-2$ | ... |
|---|---|---|---|---|---|---|
| 1 | 0 | 1 | -1 | 2 | -2 | ... |
| 2 | 0 | 1/2 | -1/2 | 2/2 | -2/2 | ... |
| 3 | 0 | 1/3 | -1/3 | 2/3 | -2/3 | ... |
| 4 | 0 | 1/4 | -1/4 | 2/4 | -2/4 | ... |
| 5 | 0 | 1/5 | -1/5 | 2/5 | -2/5 | ... |
| ... | ... | ... | ... | ... | ... | ... |
- Für Primzahlen:
- Nach dem Satz von Euklid unendlich
- Als Teilmenge der natürlichen Zahlen auch abzählbar, es gilt $P \subset \N$
- Gerade Zahlen:
- Als Teilmenge der natürlichen Zahlen abzählbar unendlich, es gilt $G \subset \Z$
Beweisen Sie den folgenden Satz: Wenn M1,M2,M3,... abzählbare Mengen sind, dann ist auch die Menge $\bigcup_{n=1}^\infty {M_{n}}$ abzählbar.
Verifizieren Sie, dass die folgende Funktion $f : \N+ \to \Q+$ eine bijektive Funktion ist und implementieren Sie eine Prozedur, die die zugehörige Umkehrfunktion $f^{-1}$ berechnet.
$$f(n) = \begin{cases} 1, & \text{wenn } n=1;\\ f(\frac{n}{2})+1, & \text{wenn } n \text{ gerade};\\ \frac{1}{f(n-1)}, & \text{wenn } n \text{ ungerade}. \end{cases}$$
Umkehrfunktion:
$$ f^{-1}(n) = \begin{cases}1, & n = 1 \\ f^{-1}(n-1) * 2, & n > 1 \\ f^{-1}(\frac{1}{n}) + 1, & sonst\end{cases} $$
- (1)
- (2)
$f(1) = 1$
$f(2) = 2$
$f(3) = 0,5$
$f(4) = 3$
$f(5) = \frac{1}{3}$
$f(6) = 1,5$
$f(7) = \frac{2}{3}$
- (3)
...
Zeigen Sie, dass die Menge der reellen Zahlen überabzählbar unendlich ist.
Mit Hilfe von Cantors zweiten Diagonalverfahren kann gezeigt werden, dass die reellen Zahlen überabzählbar unendlich sind.
Dabei wird zunächst per indirektem Beweis davon ausgegangen, dass die reellen Zahlen im Intervall (0,1) abzählbar seien.
Wenn dem so ist, könnte man jede reelle Zahl, die als $0,p_1,p_2...p_n...$ dargestellt werden kann, wie folgt in eine Reihe stecken:
$a_1=0,p_{11}p_{12}p_{13}p_{14}…$
$a_2=0,p_{21}p_{22}p_{23}p_{24}…$
$a_3=0,p_{31}p_{32}p_{33}p_{34}…$
$a_4=0,p_{41}p_{42}p_{43}p_{44}…$
$...$
Man kann sich nun eine Zahl $d = 0,d_1 d_2 d_3 ...$ wählen, wobei $d_n$ immer ungleich $p_{nn}$ ist. Dann ist $d$ von allen Zahlen der Folge verschieden. Da $d$ aber auch im Intervall (0,1) liegt, ist dies ein Widerspruch zur Annahme, dass wir alle Zahlen dieses Intervalls in der Folge aufgezählt hätten.
Beispiel:
$a_1 = 0, 1 2 3...$
$a_2 = 0, 5 6 1...$
$a_3 = 0, 9 4 7...$
$...$
Zahl 1:
$a = 0,167...$
Zahl 2:
$d = 0,278$
$d$ ist von $a$ verschieden. $a$ ist in der Liste enthalten, $d$ jedoch nicht.
Vorlesung 3
Zeigen Sie, dass die beiden folgenden Mengen entscheidbar sind. Schreiben Sie je eine entsprechende Prozedur für die jeweilige charakteristische Funktion.
(1) $A^* = \{a, b\}^* \text{ und } M \subset A^* = \{w \mid w \in A^*\text{ und } |w| = 3\}$
Die Mengen sind dann entscheidbar, wenn es eine charakteristische Funktion gibt, die für jedes Element genau entscheiden kann, ob es in der Menge enthalten ist oder nicht. Es wird jeweils wahr oder falsch zurück gegeben.
Da die Menge endlich ist, kann die Liste durchgegangen werden und für jedes Element eine Gleichheitsprüfung durchgeführt werden. Sollte es gleich sein, wird wahr zurückgegeben, ansonsten falsch.
(2) $A^* = \{a, b\}^* \text{ und } M \subset A^* = \{w=aw'|w' \in A^* \}$
Diese Menge ist ebenfalls entscheidbar, da eine Funktion so arbeiten könnte, dass sie den ersten Buchstaben überprüft ob dieser a ist, falls ja, wird das Element mit der Menge verglichen und wahr zurückgegeben, falls es existiert und falsch wenn nicht.
Wie viele berechenbare charakteristische Funktionen gibt es? Hinweis: Potenzmenge unendlicher Mengen.
Die Potenzmenge von $A^*$, also ℘$(A^*)$, ist nach Definition überabzählbar unendlich. Daher gibt es auch überabzählbar unendliche viele Mengen $M$. Der Wertebereich aller Prädikate $\chi_M$ ist $\{wahr, falsch\}$. Die Mengen $M$ bilden die Defininitionsbereiche der Funktionen $\chi_M$. Folglich gibt es ebenso viele charakteristische Funktionen $\chi_M$ wie $A^*$ Teilmengen $M$ besitzt, also überabzählbar unendlich viele. Es ist aber nicht jede Funktion berechenbar.
Zeigen Sie, dass die Menge der geraden Zahlen G eine aufzählbare Menge ist.
Wir können folgende Funktion angeben:
\[ f(n) = \left\{ \begin{array}{l l} n & \quad \text{wenn 2/n}\\ 2n & \quad \text{sonst} \end{array} \right.\]
Zeigen Sie, dass die Menge der Primzahlen $P$ aufzählbar ist.
\[ f(n) = \left\{ \begin{array}{l l} n & \quad \text{wenn } prim?(n)\\ 2 & \quad \text{sonst} \end{array} \right.\]
\[ prim?(n) = \left\{ \begin{array}{l l} wahr & \quad \text{wenn n eine Primzahl ist.}\\ falsch & \quad \text{wenn n keine Primzahl ist.} \end{array} \right.\]
Wir wissen, dass A* eine abzählbar unendliche Menge ist. Zeigen Sie, dass A* auch aufzählbar ist. Hinweis: Hierzu ist es notwendig ein Aufbauschema für A* zu entwerfen und anschließend eine Prozedur dafür zu implementieren.
Zeichen = $\{a, b, c\}$
" " $| a, b, c | aa, ab, ac, ba, bb, bc, ca, cb, cc |$ ...
Zeigen Sie, dass jede endliche Menge aufzählbar ist.
Jede endliche Menge ist per Definition abzählbar, da es eine Funktion gibt, die die Mächtigkeit der Menge bestimmen kann. Außerdem kann eine surjektive, total berechenbare Funktion $f : \N \rightarrow M$ angegeben werden.
Die Menge G der Gitterpunkte (0; 0); (0; 1); ... einer x-y-Ebene ist aufzählbar.
(1) Geben Sie eine Funktion $f$ an, die $\N$ bijektiv auf $G$ abbildet.
(2) Definieren Sie eine Ordnungsrelation $p<$ in $G$.
Anordnung durch Aufsummierung der Koordinaten und Größenrelation der x-Koordinate.
| Position | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Gitterpunkt (x,y) | (0,0) | (0,1) | (1,0) | (0,2) | (1,1) | (2,0) | (0,3) | (1,2) | (2,1) | (3,0) | (0,4) | (1,3) | (2,2) | (3,1) | (4,0) | (0,5) |
| x+y | 0 | 1 | 1 | 2 | 2 | 2 | 3 | 3 | 3 | 3 | 4 | 4 | 4 | 4 | 4 | 5 |
$(G, p_<)$ = {(0,0) < (0,1) < (1,0) < (0,2) < (1,1) < (2,0) < (0,3) < (1,2) < (2,1) < ...}
(3) Geben Sie eine Funktion k zur Berechnung der Platznummer k(x, y) des betrachteten Gitterpunktes (x, y) an.
Man kann die Cantorsche Paarungsfunktion nutzen:
$k(x,y) = \frac{(x+y)(x+y+1)}{2} + y$
Daraus können wir folgende Prozedur erstellen: