rado
Aus ProgrammingWiki
Inhaltsverzeichnis |
RADO-Funktion
Die Rado-Funktion (Busy-Beaver) $\sum : \N \rightarrow \N$, die nach dem Erfinder Tibor Rado benannt ist, berechnet die maximale Anzahl von Einsen, die eine mit n-Zuständen stoppende Turing-Maschine auf ein leeres Band schreiben kann. Die Einsen müssen nicht wie üblich hintereinander stehen und die Position des Schreibkopfs am Ende spielt keine Rolle. Beispielwerte für die Rado-Funktion: $\sum(1) = 1$, $\sum(2) = 4$, $\sum(3) = 6$, $\sum(4) = 13$, $\sum(5) \ge 4098$.
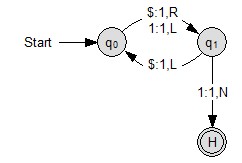
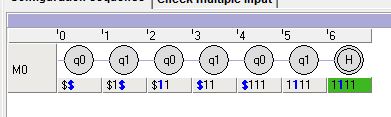
Für $n=2$ berechnet die TM $M=(\{q_0,q_1,H\},\{1\},\{\$,1\},\delta,q_0,\$,\{H\})$ den Wert $\sum(2) = 4$.
Die Rado-Funktion ist nicht Turing-berechenbar. Im Folgenden wird dies durch einen indirekten Beweis gezeigt.
Eigenschaft 1
- $\sum(n) < \sum(n + 1)$
Es gibt eine Turing-Maschine $M_n$ (zzgl. eines Haltezustands), die die Funktion $\sum(n)$ berechnet. Wird nun ein weiterer Zustand genommen und direkt nach dem Startzustand eingefügt, erhält man eine weitere Turing-Maschine $M_{n+1}$ mit $n + 1$ Zuständen. Diese erzeugt gegenüber $M_n$ mindestens eine 1 mehr, im Höchstfall $\sum(n + 1)$.
Eigenschaft 2
- Für alle $n$ gilt $f(n) \le \sum(n+k)$
Wenn $f$ eine Turing-berechenbare Funktion ist, dann existiert eine TM $M_f$. $M_f$ erzeugt mit $k$ Zuständen eine maximale Anzahl von Einsen. Bei einer TM $M_k$ werden $n$ Einsen für $n$ vorgeschaltete Zustände hinzugefügt, da $f(n)$ auf $n$ Einsen angesetzt wird. Somit kommen höchstens $n$ Zustände zu $M_k$ hinzu. Diese gesamte Maschine hat dann $n + k$ Zustände und erzuegt mindestens soviele Einsen wie $M_f$, aber höchstens $\sum(n + k)$.
Indirekter Beweis
- Annahme: $\sum$ ist berechenbar.
Wenn $f$ und $g$ Turing-berechenbare Funktionen sind, dann ist auch $g \circ f$ Turing-berechenbar, es gibt also eine TM $M_{g \circ f}$
$g$ sei in dem Fall die Funktion $v : n \rightarrow 2n$ (Verdoppler), von der wir wissen, dass sie Turing-berechenbar ist.
Wenn nun $\sum$ auch Turing-berechenbar wäre, gäbe es eine TM $M_{\sum \circ v}$, die die Funktion $(\sum \circ v)$ berechnet.
Laut Eigenschaft 2 gilt: $(\sum \circ v)(n) \le \sum(n+k)$. Verkürzt dargestellt: $\sum(v(n)) = \sum(2n) \le \sum(n+k)$.
Für ein spezielles $n$, mit $n = k + 1$ gilt: $\sum(2k+2) \le \sum(2k + 1)$.
Laut Eigenschaft 1 muss jedoch gelten $\sum(2k+2) < \sum(2k + 1)$, was einen Widerspruch darstellt.
Daher ist die Rado-Funktion nicht Turing-berechenbar.