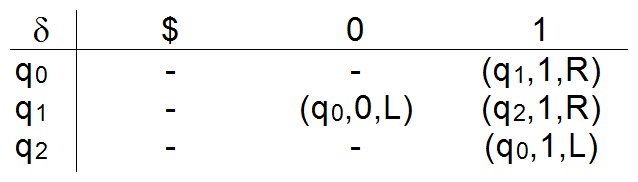Aus ProgrammingWiki

Universelle Turingmaschine

(1) Verwenden Sie kfG Edit aus AtoCC, um die folgende kontextfreie Grammatik G für die Sprache der TM-Codierungen zu definieren.

G = (N, T, P, s) N = {TMcodierung, Trenner, Endzustaende, Delta, Uebergang, Kopfbewegung, L, R, N, Zeichen, Null, Eins, B, Zustand, Einsenfolge} T = {0, 1} P = { TMcodierung -> Delta Trenner Endzustaende Trenner -> 0 0 Endzustaende -> Zustand 0 Endzustaende | Zustand Delta -> Uebergang 0 Delta | Uebergang Uebergang -> Zustand 0 Zeichen 0 Zustand 0 Zeichen 0 Kopfbewegung Kopfbewegung -> L | R | N L -> 1 R -> 1 1 N -> 1 1 1 Zeichen -> Null | Eins | B Null -> 1 Eins -> 1 1 B -> 1 1 1 Zustand -> Einsenfolge Einsenfolge -> 1 | 1 Einsenfolge } s = TMcodierung

---

(2) Als Beispiel betrachten wir die Turingmaschine

$M = (\{q_{0},q_{1},q_{2}\},\{\text{0},\text{1}\},\{\$,\text{0},\text{1}\},\delta,q_{0},\$,\{q_{0},q_{1}\})$

Verwenden Sie AutoEdit (aus AtoCC) und simulieren Sie die Anwendung von $M$ auf diverse Eingabewörter. Darunter sollte es Wörter $w$ geben, für die $M(w)$

• in einem Endzustand stoppt ($\epsilon$, 0, 1, 0101010110),
• in einem Nicht-Endzustand stoppt (11, 111, 1111),
• nicht stoppt (10).

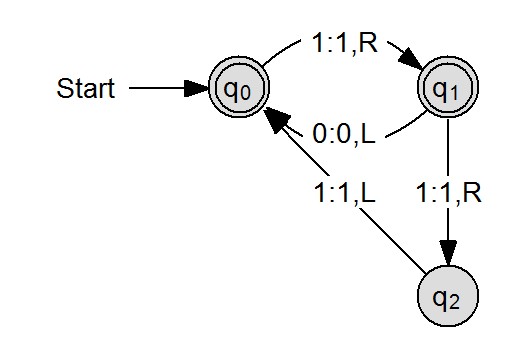
Schauen Sie sich auch den Übergangsgraph von $M$ an.

---

(3) Kodieren Sie $M$ aus dem Beispiel per Hand, indem Sie die folgenden Kodierungsregeln befolgen:

Symbol	Kodierung
0	1
1	11
B	111
$q_0$	1
$q_1$	11
$\vdots$	$\vdots$
$q_n$	$1^{n+1}$
L	1
R	11
N	111

{q0,1} -> {q1,1,R} 1 0 11 0 11 0 11 0 11 {q1,0} -> {q0,0,L} 11 0 1 0 1 0 1 0 1 {q1,1} -> {q2,1,R} 11 0 11 0 111 0 11 0 11 {q2,1} -> {q0,1,L} 111 0 11 0 1 0 11 0 1

Zusätzlich müssen die Endzustände definiert werden.

q0, q1 1 0 11

Daraus ergibt sich die folgende Kodierung $\langle M \rangle$ :

1 0 11 0 11 0 11 0 11 0 11 0 1 0 1 0 1 0 1 0 11 0 11 0 111 0 11 0 11 0 111 0 11 0 1 0 11 0 1 00 1 0 11

---

(4) Als nächstes soll ein Compiler entwickelt werden, der ein syntaktisch korrektes Wort aus $L(G)$, also eine korrekte TM-Codierung, in eine TM in der AtoCC-Repräsentation übersetzt.

(a) Die reduzierte Grammatik ohne die Regel $Trenner -> 0 0$ da es sonst zu shift-reduce-Konflikten kommen kann.

G = (N, T, P, s) N = {TMcodierung, Trenner, Endzustaende, Delta, Uebergang, Kopfbewegung, L, R, N, Zeichen, Null, Eins, B, Zustand, Einsenfolge} T = {0, 1} P = { TMcodierung -> Delta Trenner Endzustaende Endzustaende -> Zustand 0 Endzustaende | Zustand Delta -> Uebergang 0 Delta | Uebergang Uebergang -> Zustand 0 Zeichen 0 Zustand 0 Zeichen 0 Kopfbewegung Kopfbewegung -> L | R | N L -> 1 R -> 1 1 N -> 1 1 1 Zeichen -> Null | Eins | B Null -> 1 Eins -> 1 1 B -> 1 1 1 Zustand -> Einsenfolge Einsenfolge -> 1 | 1 Einsenfolge } s = TMcodierung

(b) Struktur des Zieldokuments mit weggelassenen Layout-Eigenschaften

<?xml version="1.0" encoding="utf-8"?> <AUTOMATON> <TYPE value="TM"/> <ALPHABET> <ITEM value="0"/> <ITEM value="1"/> </ALPHABET> <TAPEALPHABET> <ITEM value="$"/> <ITEM value="0"/> <ITEM value="1"/> </TAPEALPHABET> <STATE name="q_0" finalstate="true"> <TRANSITION target="q_1"> <LABEL read="1" direction="RIGHT" write="1" /> </TRANSITION> </STATE> <STATE name="q_1" finalstate="true"> <TRANSITION target="q_0"> <LABEL read="0" direction="LEFT" write="0" /> </TRANSITION> <TRANSITION target="q_2"> <LABEL read="1" direction="RIGHT" write="1" /> </TRANSITION> </STATE> <STATE name="q_2" finalstate="false"> <TRANSITION target="q_0"> <LABEL read="1" direction="LEFT" write="1" /> </TRANSITION> </STATE> <INITIALSTATE value="q_0" /> <TAPEINITIALCHAR value="$" /> </AUTOMATON>

(c) Beschreiben und Erzeugen des Compilers