vorlesung4
Aus ProgrammingWiki
Definieren Sie je eine totale Funktion fur den Vorgänger und die Halbierung einer natürlichen Zahl. Definieren Sie außerdem eine Funktion mit $D_f = \N \backslash \{1234, 7266281\}$.
- (a) Vorgänger der natürlichen Zahl:
\[ f(n) = \left\{ \begin{array}{l l} n-1 & \quad \text{wenn } n>0\\ 0 & \quad \text{sonst} \end{array} \right.\]
- (b) Halbierung einer natürlichen Zahl:
\[ f(n) = \left\{ \begin{array}{l l} \frac{n}{2} & \quad \text{wenn } n|2\\ \frac{n+1}{2} & \quad \text{sonst} \end{array} \right.\]
- (c) $D_f = \N \backslash \{1234, 7266281\}$:
\[ f(n) = \left\{ \begin{array}{l l} n & \quad \text{wenn } n \neq 1234, 7266281\\ \perp & \quad \text{sonst} \end{array} \right.\]
Für $K = ((001, 0)(01, 011),(01, 101),(10, 001))$ gibt es eine Lösung. Die gesuchte Indexfolge heißt:
$(2 4 3 4 4 2 1 2 4 3 4 3 4 4 3 4 4 2 1 4 4 2 1 3 4 1 1 3 4 4 4 2 1 2 1 1 1 3 4 3 4 1 2 1 4 4 2 1 4 1 1 3 4 1 1 3 1 1 3 1 2 1 4 1 1 3)$
Überprüfen Sie die angegebene Lösung per Hand.
X = $0110011010010010110011001101001101001001101001001011000100101101010010010100100100101100110001010011010010011000100101100010010100100101001010011000100101$
Y = $0110011010010010110011001101001101001001101001001011000100101101010010010100100100101100110001010011010010011000100101100010010100100101001010011000100101$
Entwickeln Sie eine Scheme-Prozedur (vorhandene ProgrammingWiki-Lösung verwenden), die bei Aufruf für eine gegebene Instanz eine Lösung des PCP findet, falls eine solche existiert (und der Rechenaufwand im Rahmen bleibt).
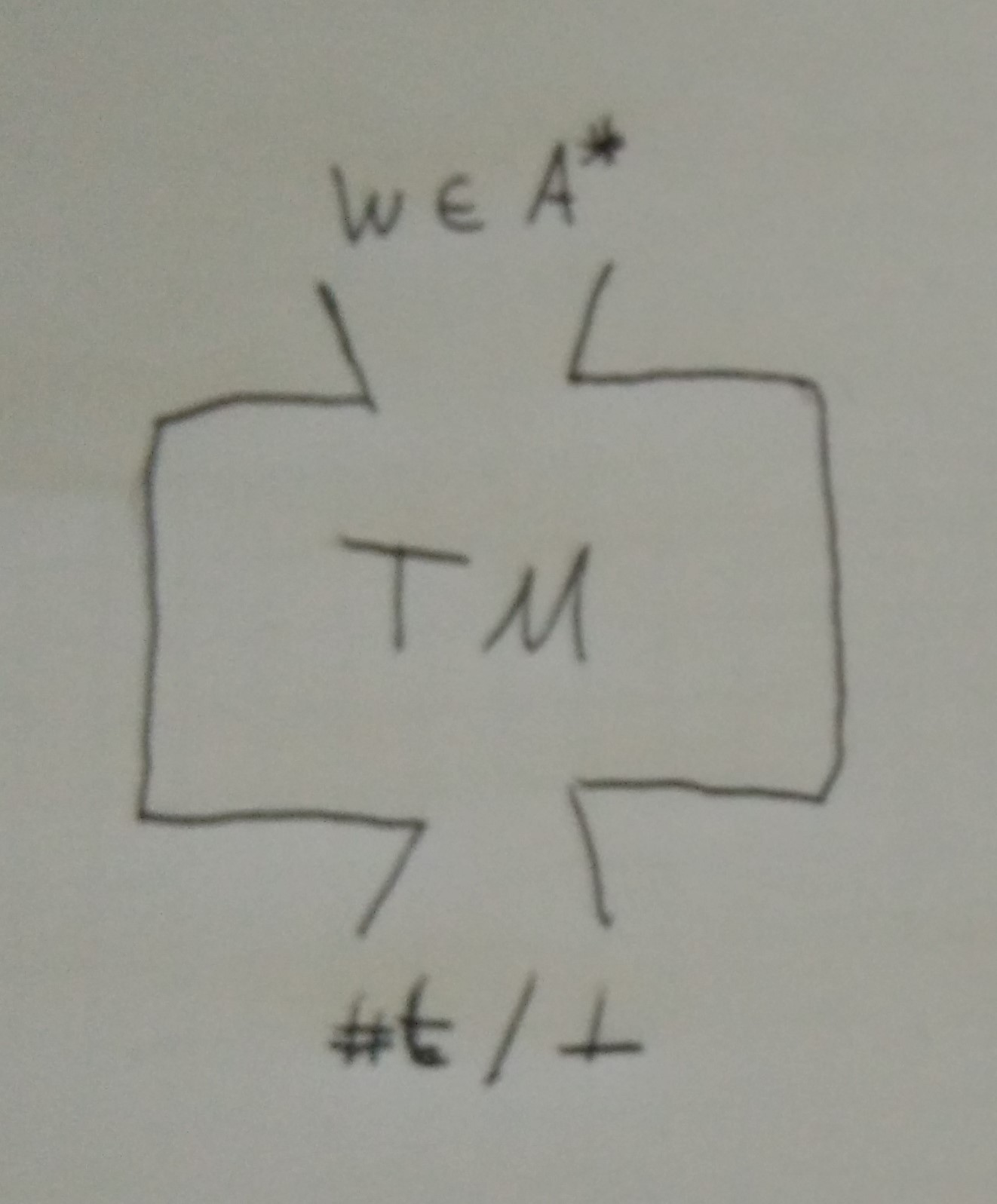
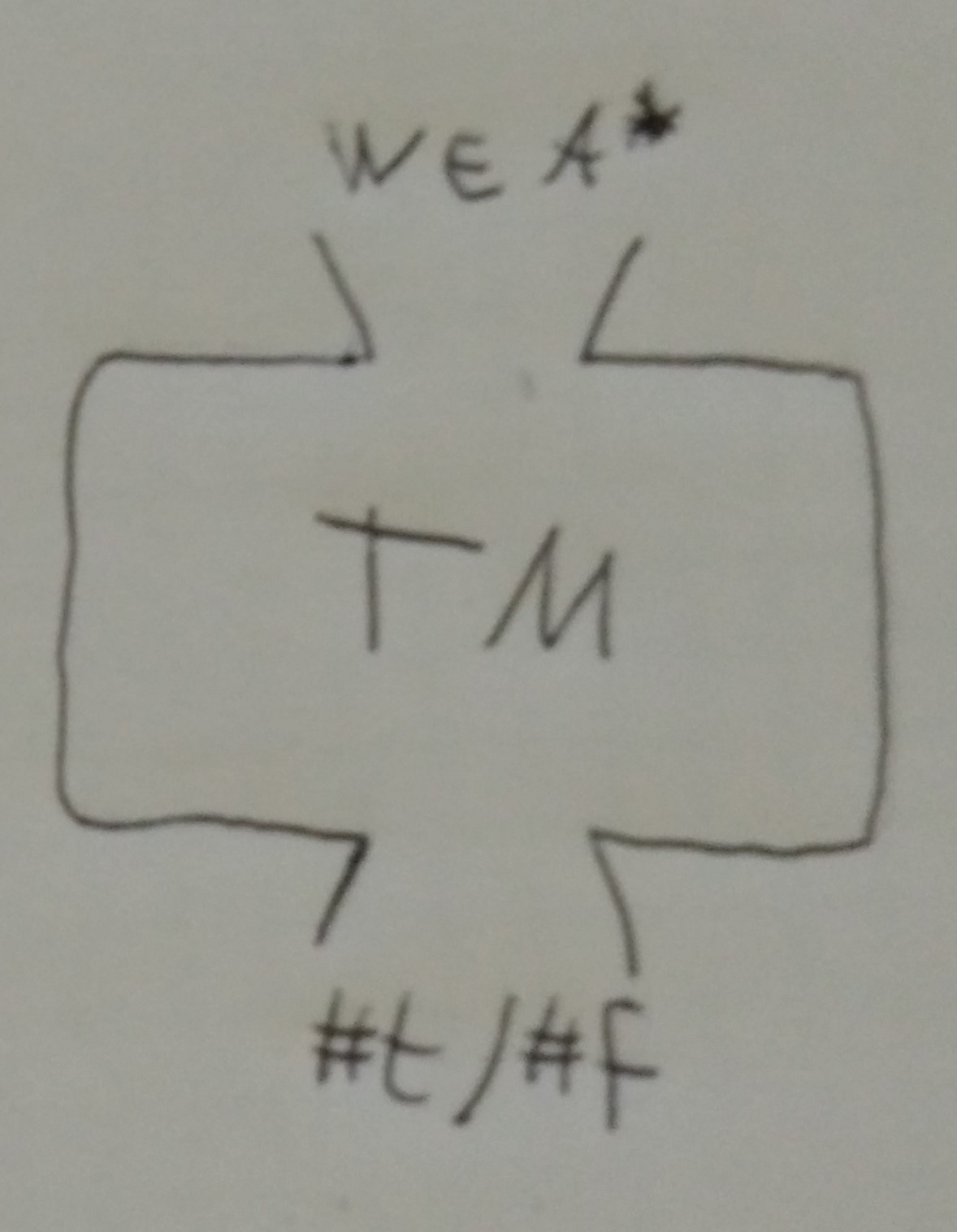
Geben Sie Trichterbilder fur den Einsatz einer TM als Akzeptor an:
- semi entscheidbare Sprachen:
- entscheidbare Sprachen:
Definieren Sie die Begriffe Turing-aufzählbar und Turing-entscheidbar analog zur Turing-Berechenbarkeit.
Sei $A$ ein Alphabet, $M \subseteq A^*$. $M$ heißt Turing-entscheidbar, falls die charakteristische Funktion $\chi_M$ Turing-berechenbar ist.
M heißt Turing-aufzählbar, wenn es eine Funktion $f : \N \rightarrow M$ gibt, die surjektiv und Turing-berechenbar ist.