Hamilton Kreise
Aus ProgrammingWiki
Inhaltsverzeichnis |
Einführung
Definitionen Graphentheorie
Einfacher Weg
Für $n ≥ 2$ nennt man einen Graphen $P_n$ mit der Knotenmenge $V(P_n)$ = {$v_0$, $v_1$, . . . , $v_n$} und der Kantenmenge $E(P_n)$ = {{$v_0$, $v_1$}, {$v_1$, $v_2$}, . . . , {$v_{n−1}$, $v_n$}} einen einfachen Weg der Länge $n$, sofern keine Kante und kein Knoten mehrfach durchlaufen wird.
siehe auch: Grundbegriffe der Graphentheorie 1
Einfacher Kreis
Für $n ≥ 3$ nennt man einen Graphen $P_n$ mit der Knotenmenge $V(P_n)$ = {$v_0$, $v_1$, . . . , $v_n$} und der Kantenmenge $E(C_n)$ = {{$v_0$, $v_1$}, {$v_1$, $v_2$}, . . . , {$v_{n−1}$, $v_n$}} einen einfachen Weg (oder Pfad) der Länge $n$, sofern keine Kante und kein Knoten mehrfach durchlaufen wird.
siehe auch: Grundbegriffe der Graphentheorie 1
Bewerteter Graph
| kantenabhängig | knotenabhängig |
|---|---|
| Eine Kantenmarkierung eines Graphen $G =(V, E)$ ist eine Abbildung $b:E \rightarrow M$ die jeder Kante $e$ einen Wert oder ein Symbol zuordnet. Für die Bewertung der Kante {$u, v$} schreiben wir dann kurz $b(u, v)$. | Eine Knotenmarkierung eines Graphen $G =(V, E)$ ist eine Abbildung $b:V \rightarrow M$ die jedem Knoten $v$ einen Wert oder ein Symbol zuordnet. |
siehe auch: Grundbegriffe der Graphentheorie 2

Dijkstra-Algorithmus
Der Dijkstra-Algorithmus gehört in die Gruppe der Greedy-Algorithmen. Er dient zur Berechnung der kürzesten Pfade von einem bestimmten Startknoten aus.
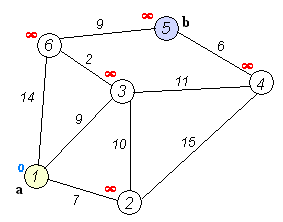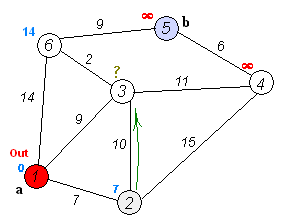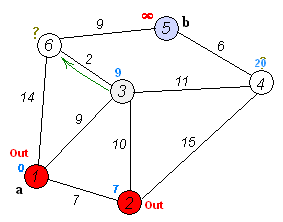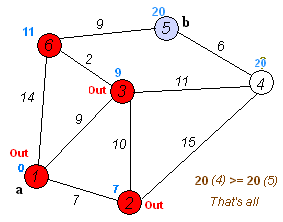
siehe auch: Kürzeste Wege in Graphen
Hamilton Graphen
Das Euler-Kreis-Problem behandelt die Kantenproblematik. Das Hamilton-Kreis-Problem ist das Gegenstück davon. Es handelt sich also um Knotenproblem.
Gegeben ist ein beliebig großer Graph. Wir suchen nun einen Teilgraph, der alle $n$ Knoten des Graphen einmal durchläuft.
Es sei $G = (V,E)$ ein Graph mit $n$ Knoten. Der Teilgraph $C$, der alle $n$ Knoten genau einmal durchläuft nennt man Hamilton Graph.
Hamiliton Wege
Ein Hamilton Weg ist, wie der Name schon sagt ein Weg, um genau zu sein ein einfacher Weg, da jeder Knoten nur einmal benutzt werden muss. Wenn in dem Graphen ein Hamilton Weg zu finden ist, so nennt man den Graphen auch semihamiltonisch.
Es sei $G = (V,E)$ ein Graph mit $n$ Knoten. Ein Teilgraph $C$ heißt Hamilton Weg, wenn der Teilgraph ein einfacher Weg ist, der alle $n$ Knoten genau einmal durchläuft. Der Graph $G$ wird dann auch als semihamilonisch bezeichnet.
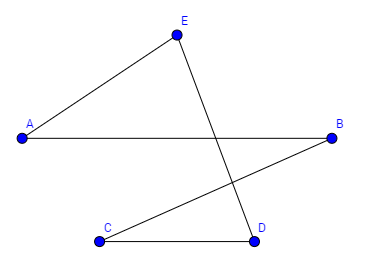
Beispiel Hamilton Weg:
Finden sie ein Hamilton Weg.
Hamilton Kreise
Wenn wir von einem Hamilton Kreis sprechen ist in dem Graphen ein einfacher Kreis enthalten, der alle Knoten des Graphen berührt. Diesen Graphen nennt man hamiltonisch.
Es sei $G = (V,E)$ ein Graph mit $n$ Knoten. Ein Kreis $C$ auf $G$ heißt Hamilton Kreis, falls er jeden der $n$ Knoten von $G$ genau einmal durchläuft. $G$ heißt dann auch hamiltonischer Graph.
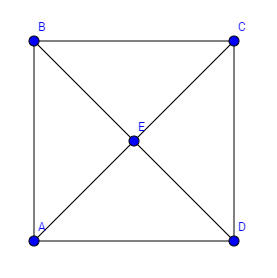
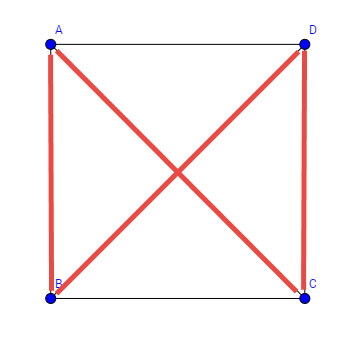
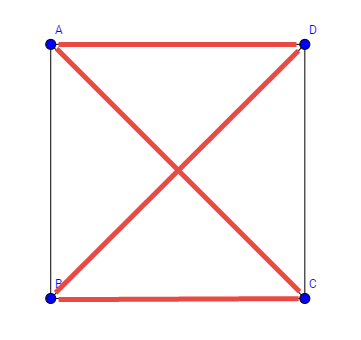
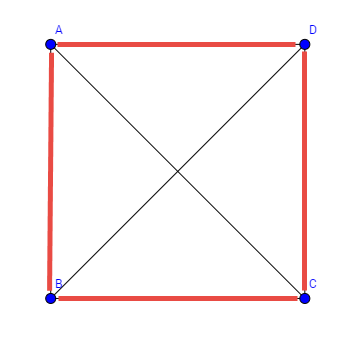
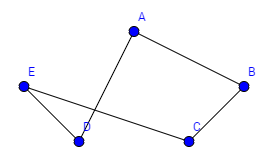
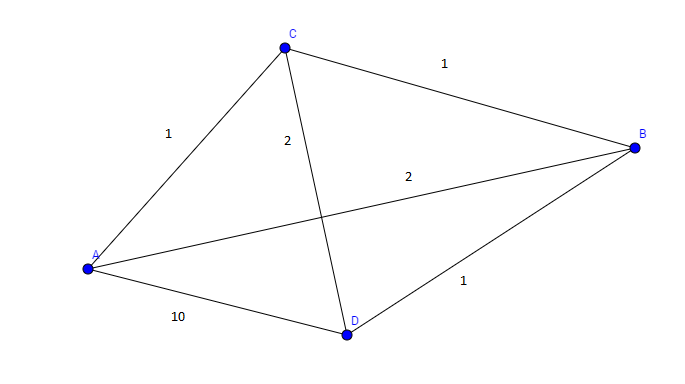
Beispiel mit 4 Knoten: Hier ist nun ein Graph mit 4 Knoten und ziemlich vielen Kanten gegeben. Das macht die Suche relativ einfach. Tragen sie alle möglichen Hamilton Kreise zusammen.
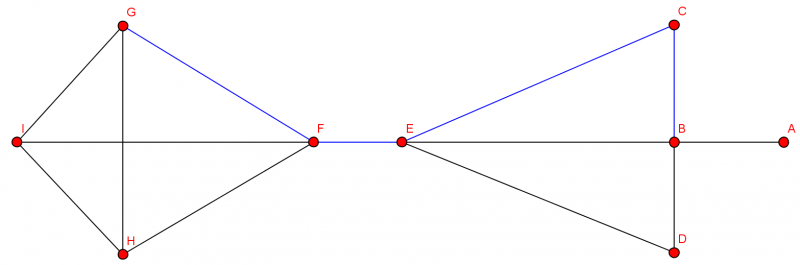
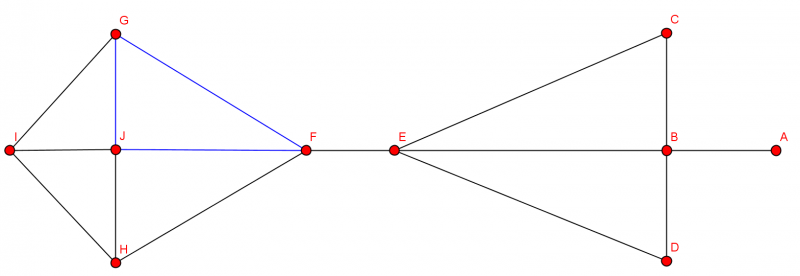
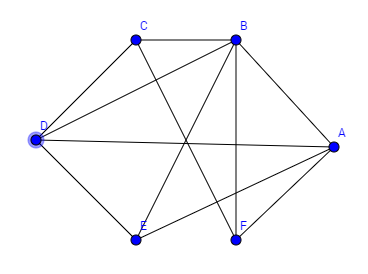
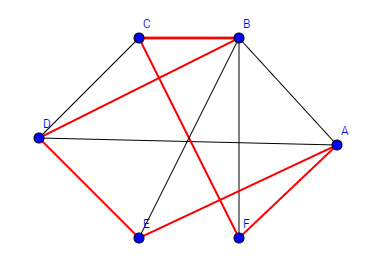
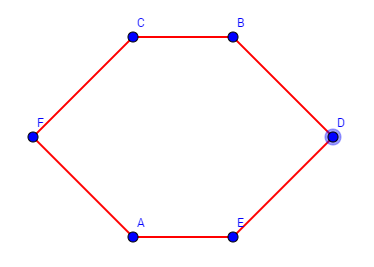
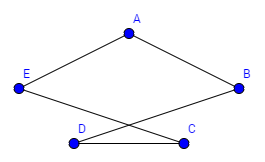
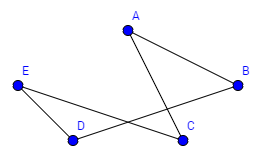
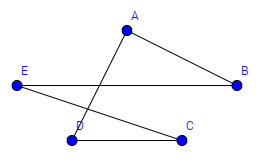
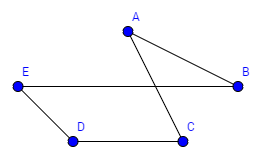
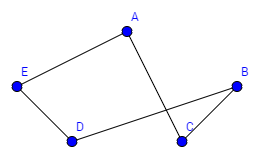
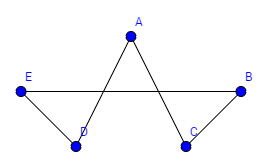
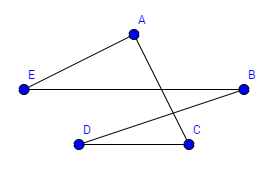
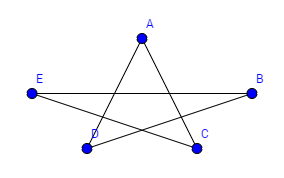
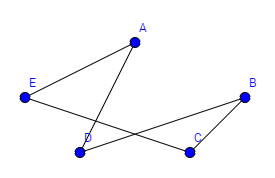
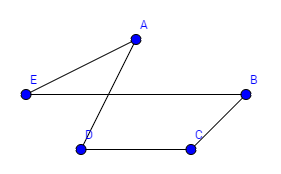
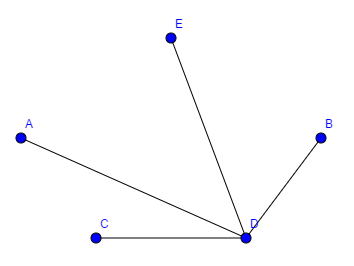
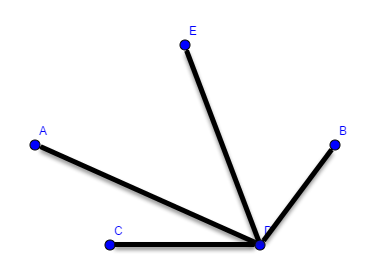
Beispiel Bekanntheitsgraph:
Wir wollen eine Geburtstagsparty feiern. Wir haben verschieden Leute eingeladen und wollen nun die beste Tischordnung finden, dass jede Person eine bekannte Person an seiner rechten und eine bekannte an seiner linken Seite hat. Finden Sie einen Kreis, der diese Kriterien erfüllt. Entfernen sie dann alle Kanten, die nicht zum Graphen gehören und ordnen sie den Graphen.
Man merkt, dass es immer schwieriger wird ein Hamilton Kreis zu finden. Es gibt kein effizientes Verfahren, der uns die Existenz und das Finden des Kreises erleichtert.
Naive Suche
Gäbe es ein Kriterium für die Existenz eines Hamilton Kreises wäre das Finden des Kreises leichter, da man weiß, dass es mindestens einen Hamilton Kreis gibt. Dies ist ab einer bestimmten Größe nicht mehr effizient.
Unter der Annahme, dass $10^{30}$ Lösungen pro ns berechnet werden können. Kann man zu folgender sehr erstaunlichen Tabelle kommen.
| Anzahl Knoten | Anzahl möglicher Lösungen | Benötigte Zeit |
|---|---|---|
| 5 | $12$ | |
| 10 | $181440$ | |
| 15 | $4,36 \cdot 10^{10}$ | |
| 20 | $6,08 \cdot 10^{16}$ | |
| 25 | $3,1 \cdot 10^{23}$ | |
| 30 | $4,42 \cdot 10^{30}$ | 4,42 ns |
| 35 | $1,48 \cdot 10^{38}$ | 0,15 s |
| 40 | $1,02 \cdot 10^{46}$ | 118 Tage |
| 45 | $1,33 \cdot 10^{54}$ | $9,21 \cdot 10^7$ Jahre |
| 50 | $3,04 \cdot 10^{62}$ | $9,6 \cdot 10^{15}$ Jahre |
Gedankenexperiment:
Wir haben einen gegeben Graphen. Hat das hinzufügen einer Kante Auswirkungen auf die Existenz eines Hamilton Graphen bzw. Hamilton Kreis.
JA desto mehr Kanten im Graph sind, umso wahrscheinlicher ist es, dass der Graph semihamiltonisch oder sogar hamiltonisch ist. Aus diesem Experiment hat Paul Dirac (1952) als erster Wissenschaftler sich diesem Problem angenommen und den folgenden Satz formuliert:
Dass der Grad jedes Knotens mindestens $\tfrac{n}{2}$ beträgt, ist eine hinreichende, jedoch keine notwendige Bedingung dafür, dass der Graph hamiltonisch ist.
In folgendem Beispiel gelten $n=9$ und der Mininmalgrad aller Knoten ist $2$. Dennoch ist der Graph hamiltonisch.
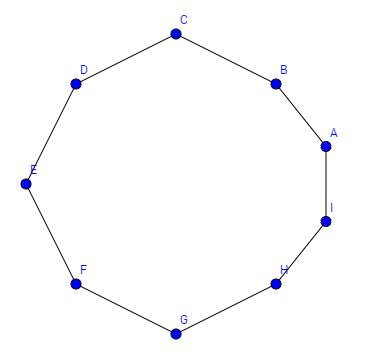
In den folgenden Jahren fand man Bedingungen für die Existenz eines Hamilton Kreises:
- Entfernt man aus einem hamiltonischen Graphen einen Knoten, so bleibt der Graph zusammenhängend.
- Ein hamiltonischer Graph mit $n$ Knoten hat einen Durchmesser (maximaler Abstand zwischen 2 Knoten) von höchstens $\dfrac{n}{2}$
Diese Bedingungen zeigen, dass ein Graph nicht hamiltonisch ist. Dies ist eigentlich nicht das gesuchte Ziel. Man kann es aber trotzdem benutzen. Nachteilig ist außerdem, dass man jeden Knoten probieren muss, um den Minimalgrad der Aussage bestimmen zu können. Die Komplexität ist $\mathcal O = 2^n$.
Code
Anzahl an Hamilton Kreisen
Voraussetzung: Jeder Knoten ist mit jedem Knoten durch eine Kante verbunden. Es handelt sich um einen vollständigen Graphen.
Begründung: Wir starten an einem beliebigen Startknoten, der eine Anzahl $n$ an Kanten hat. Wir haben $n-1$ Möglichkeiten die richtige Kante zum nächsten Knoten zu wählen. An diesem Knoten habe wir nur noch $n-2$ Kanten zur Wahl, da 2 Kanten zu bereits durchlaufenen Knoten führen. An dem nächsten Knoten haben wir dann nur noch die Wahl aus $n-3$ Möglichkeiten. Daraus ergibt sich dann $(n-1)!$.
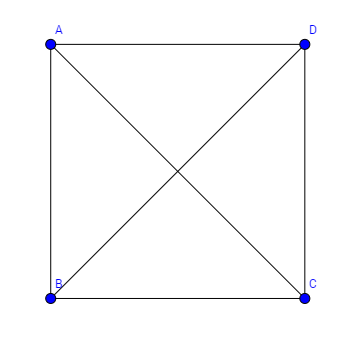
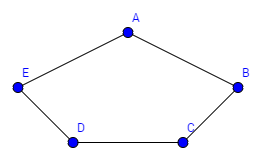
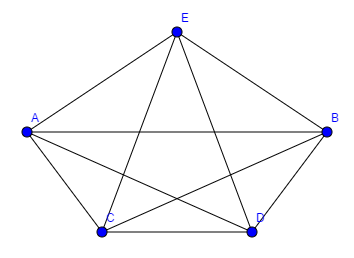
Beispiel: Wir haben einen vollständigen Graphen mit 5 Knoten. Wie viele Hamilton Kreise kann man finden?
Kritische Betrachtung des Verfahrens: Wie viele Hamilton Kreise kann man für eine Knotenanzahl von 20 Städten finden?
Eine Auflistung und Auswahl des minimalen Kreises gestaltet sich als sehr schwierig, da bei einer relativ geringen Anzahl an Knoten eine mächtige Menge von Hamilton Kreisen zustande kommt. Wenn wir jetzt durch die gesamte Menge durch iterieren wollen ist der Aufwand extrem.
Beweis der Komplexität (Stirlingsche Formel)
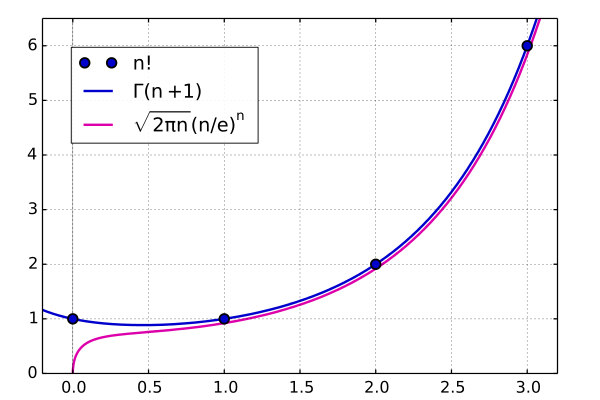
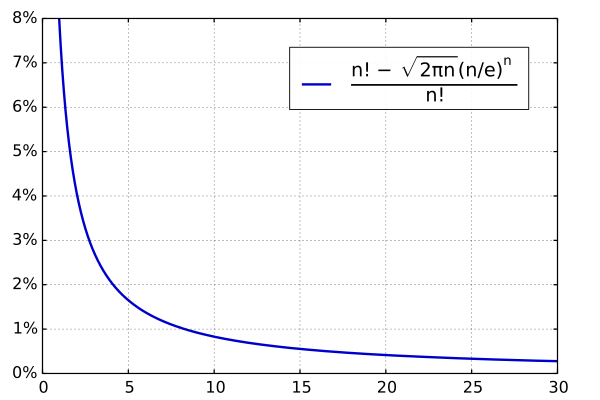
Zum Beweis der Komplexität ziehen wir die Stirlingsche Formel zur Hilfe. Diese hat ähnliche Eigenschaften, wie die Fakultät und hat eine sehr geringe Abweichung von der Fakultät.
Die Stirlingsche Formel lautet: $$n! \sim \sqrt{2 \pi n} (\dfrac{n}{e})^n; n \rightarrow \infty$$ Aus dieser Grundformel kann man dann auf die folgende Gleichung kommen. Mehr Informationen dazu gibt es hier [1]. $$n! = \sqrt{2 \pi n} (\dfrac{n}{e})^n (1+\dfrac{1}{12n}+\dfrac{1}{288n^2}+\mathcal O (\dfrac{1}{n^3}))$$ Aus dieser Formel lässt sich dann der exponentielle Aufwand herleiten.
Traveling Salesman Problem (TSP)
Das TSP ist ein klassischer Anwendungsfall der Hamilton Kreise. Das Ziel des TSP liegt darin, die günstigste Reise in einem bewertetem Graphen durch alle Orte zu finden. Seit mehreren Generationen ist dies ein sehr wichtiges Problem. Durch die sehr einfache Vorstellung des Problems ist die Einarbeitung in das Problem sehr einfach. Leider gibt es keinen allgemeinen Lösungsansatz, der das Problem in adäquater Zeit löst. Heuristiken können zwar eine Lösung bieten, diese kann aber sehr ungenau sein und wird dadurch nicht als befriedigend eingestuft.
Das Problem des Handlungsreisenden (Travelling Salesman Problem) besteht darin, auf einem vollständigen bewerteten Graphen $K_n$ einen (im Sinne der Bewertung) kürzesten Hamilton-Kreis zu finden. Gilt für die Bewertung zuätzlich die Dreiecksungleichung, so spricht man von einem Rundreiseproblem.
Dreiecksungleichung
Die Dreiecksungleichung entspricht dem normalen Entfernungsverständnis im Alltag. Wenn ich also von Görlitz nach Dresden fahren möchte fahre ich nicht über Berlin, weil dieser Weg länger ist und ein direkter Weg vorliegt.
Im vollständigem Graphen $K_n$ ist die Dreiecksungleichung erfüllt, wenn für alle Knoten $u$,$v$ und $w$ gilt: $$d(u,v) \leq d(u,v)+d(w,v)$$
Erschöpfende Suche
Die erschöpfende Such oder auch exhaustive search dient zur Berechnung der kompletten Menge aller Lösungen des Problems. Die Lösungsmenge enthält in jedem Fall die optimale Lösung. Diese herauszufinden kann je nach Problem sehr einfach sein z.B. durch einen Vergleich der Kosten.
In unserem Fall ist es theoretisch einfach so etwas aufzubauen, jedoch wird die Berechnungszeit bei größeren Graphen enorm ansteigen. Wir müssten für jeden Knoten $n$ aus unserem Graphen $K_n$ einen Hamilton Kreis finden. Aus dieser entstehende Menge müsste man den Kreis herausfinden, der das geringste Gewicht hat.
Komplexitätsklassen
Bisher haben wir die Komplexität von bestimmten Algorithmen im Einzelnen betrachtet. In der Komplexitätstheorie werden Algorithmen bezüglich ihres unterschiedlichen Aufwands in Klassen eingeteilt. Zur Einteilung in diese Klassen sind die elementaren Rechenschritte von Bedeutung.
Die time und TIME Funktion
Als Voraussetzung muss der entsprechende Algorithmus als Turing-Programm formuliert sein.
- $time(w) = \text{Anzahl der Rechenschritte der TM bei eingabe von}$ $ w$
- $TIME(f) = \lbrace L \subseteq \Sigma^{*} | \text{ Es gibt eine TM mit } L = L(TM) \text{ und } time(w) \leq f(|w|) \text{ für alle } w \in L\rbrace$
Die Komplexitätsklasse P
- Die Klasse P lässt sich definieren als Klasse aller Probleme, die mit deterministischen Algorithmen in polinomialer Zeit gelöst werden können.
Definition mit Hilfe der Turingmaschine:
- Diese Problemklasse lässt sich effizient mit Algorithmen lösen.
Die Komplexitätsklasse NP
- Die Komplexitätsklasse der NP-Probleme ist die Menge aller Probleme, die nichtdeterministisch in Polynomzeit gelöst werden können.
Definition mit Hilfe der Turingmaschine:
- In dieser Klasse gibt es keine effizienten Algoritmen zur Lösung der Probleme.
Heuristiken
Motivation
Von Bedeutung sind diese Verfahren, wenn es zwar theoretisch optimale Lösungen für bestimmte Probleme gibt, diese jedoch in der Praxis aufgrund extrem langer Rechenzeiten verworfen werden müssen.
Begriff
Der Begriff Heuristik stammt von dem griechischen Wort "heurisko" ab, das übersetzt etwa "ich finde", "ich suche" bedeutet.
Definition
Heuristiken sind durch Erfahrung gewonnene Regeln und Verfahren, die in akzeptabler Zeit zu einer zufriedenstellenden Lösung führen. Man weiß zwar nicht, ob die gefundene Lösung optimal ist, man ist aber mit dem Ergebnis zufrieden, wenn sich abschätzen lässt, wie gut oder wie schlecht die gefundene Lösung ist. Durch Probieren wird versucht das Ergebnis weiter zu verbessern.
Es handelt sich um Faustregeln oder Handlungsempfehlungen, basierend auf intuitiven Regeln, ähnlich den Bauernregeln für das Wetter. Aus einer Vielzahl von Möglichkeiten werden einige herausgefiltert.
Beispiele hierfür sind:
- das 0/1 Rucksackproblem,
- das TSP,
- das Springerproblem beim Schach.
Heuristiken und Algorithmen
| 1. Fall | 2. Fall |
|---|---|
| Es gibt eine exakte Lösung des Problems. | Es gibt keine exakte Lösung des Problems. |
| Anwendung eines Verfahrens/Algorithmus, welches das Optimalitätskriterium für ein bestimmtes Problem erfüllt. | Das Optimalitätskriterium wird nicht immer erfüllt. |
| Hier spricht man von einem Algorithmus. | Diese Verfahren können Heuristiken sein. |
Also kann man festhalten: $Heuristiken \subset Algorithmen$.
- Wenn die Lösung nicht exakt ist, bleibt die Frage nach Ihrer Güte.
- D. h. wie groß ist die Abweichung von dem exakten Ergebnis?
- Diese Betrachtung in Bezug auf die Heuristiken erfolgt weiter unten!
Heuristiken für das TSP
Nearest-Neightbor-Heuristik
Ein weiterer Name dafür ist der "Best-Successor-Algorithmus", man spricht ebenfalls von der "Methode des Besten Nachfolgers".
Gruppe:
Greedy Algorithmen
Aufbau
Allgemeine Greedy Charakteristik
- lokale Suche nach bestem Nachfolger (Happen)
- kein Backtracking, revidieren der Entscheidung
- keine vorübergehende Verschlechterung durch Vorausschau
Prinzipelles Vorgehen des Verfahrens
Eingabe: Vollständig bewerteter Graph $K_n$
| Schritt 1: | Beginne an einem beliebigen Knoten mit leerer Tour $v \in V$ und $T = \emptyset$. |
| Schritt 2: | Bestimme einen noch nicht besuchten Knoten, mit der geringsten Entfernung zu $v$ $w \ne v$ und setze $T = T \cup \{v,w\}$, sowie $v = w$. |
| Schritt 3: | Solange es noch unbesuchte Knoten gibt, gehe zu Schritt 2. Ansonsten gehe zurück zum Anfang $v$ und füge $v$ der Tour hinzu $T = T \cup \{v\}$ |
Ergebnis: Hamilton-Kreis
Beispiel für ein TSP
Wenden sie die Greedy Heuristik auf alle möglichen Startpunkte an und geben sie alle Touren und Kosten an.
Komplexität der Heuristik
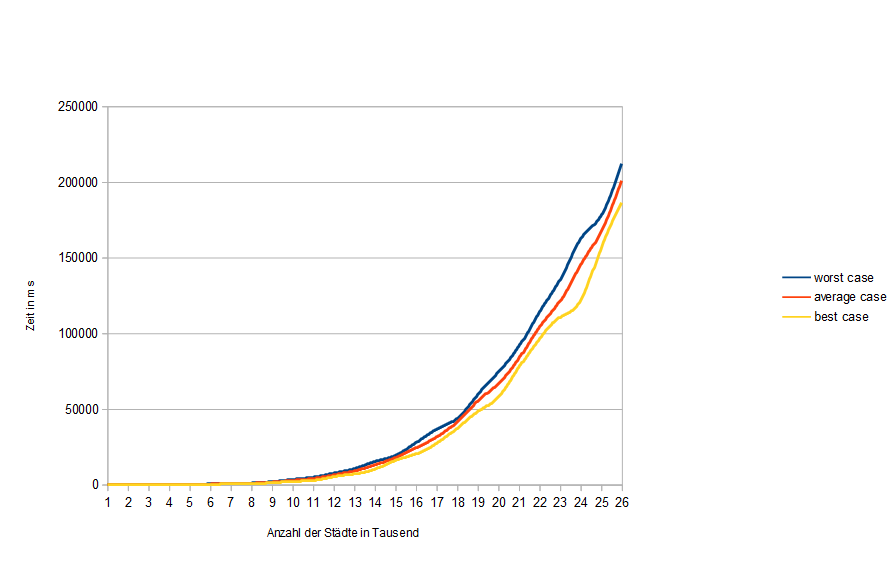
Die Komplexität der Heuristik beträgt $\mathcal O(n^2)$ laut Literatur. Somit liegt die Heuristik in der Komplexitätsklasse P und ist effizient lösbar.
Die empirische Laufzeitanalyse ergab folgende Werte.
Implementation
Vor- und Nachteile
| Vorteile | Nachteile |
|---|---|
| schnelles Verfahren | keine optimalen Ergebnisse |
| geeignet für große Problemgrößen | keine globale suche |
| praktikabel | |
| kann ein praktisch unlösbares Problem lösen |
Insertion-Heuristiken
Es gibt unterschiedliche Insertion Heuristiken, bei denen, wie der Name vermuten lässt, in eine bestehende Tour Knoten eingefügt werden. Man unterscheidet folgende Heuristiken: Farthest-Insertion, Random-Insertion und Best-Insertion. Im Folgenden wird auf Random-Insertion eingegangen.
Gruppe:
Greddy Algorithmen
Prinzipielles Vorgehen des Verfahrens
Eingabe: Vollständig bewerteter Graph $K_n$
| Schritt 1: | Wähle 3 Startknoten und bilde eine Rundreise durch diese. | |
| 1.1 Diese Tour besteht aus 3 Toursegmenten, nämlich den Kanten zwischen den vorhandenen Knoten. | ||
| Schritt 2: | Solange noch Knoten existieren, die noch nicht der Tour hinzugefügt wurden, wiederhole die folgenden Schritte | |
| 2.1 Wähle zufällig einen noch nicht zur Tour hinzugefügten Knoten Z aus. | ||
| 2.2 Berechne die Distanz von Z zu allen Knoten in der Tour. | ||
| 2.3 Bestimme die zwei benachbarten Knoten P und Q der bisherigen Tour, sodass, wenn man Z zwischen Ihnen einfügt, die aktuelle Rundreise minimal verlängert wird. | ||
| 2.4 Füge Z zur aktuellen Tour hinzu, indem die Strecke PQ durch PZ und ZQ ersetzt wird. |
Ergebnis: $Hamilton-Kreis$
Beispiel
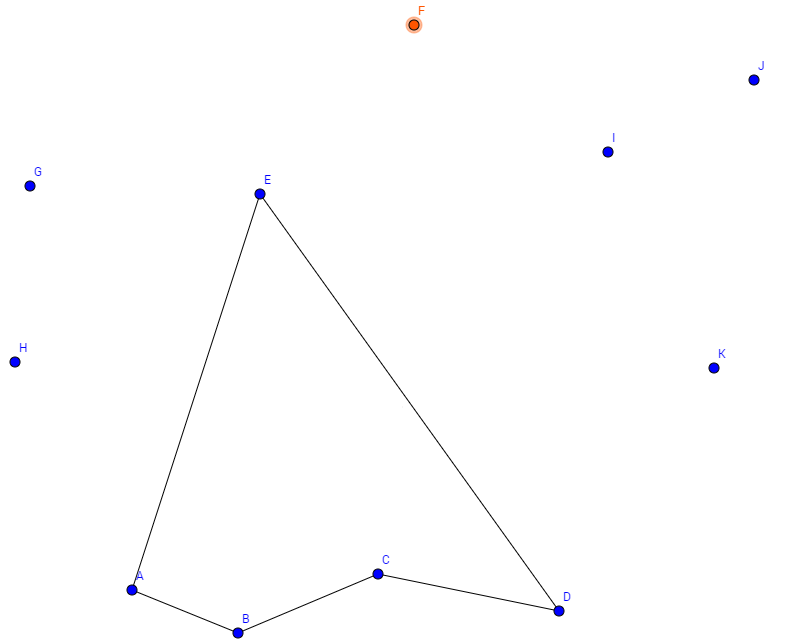
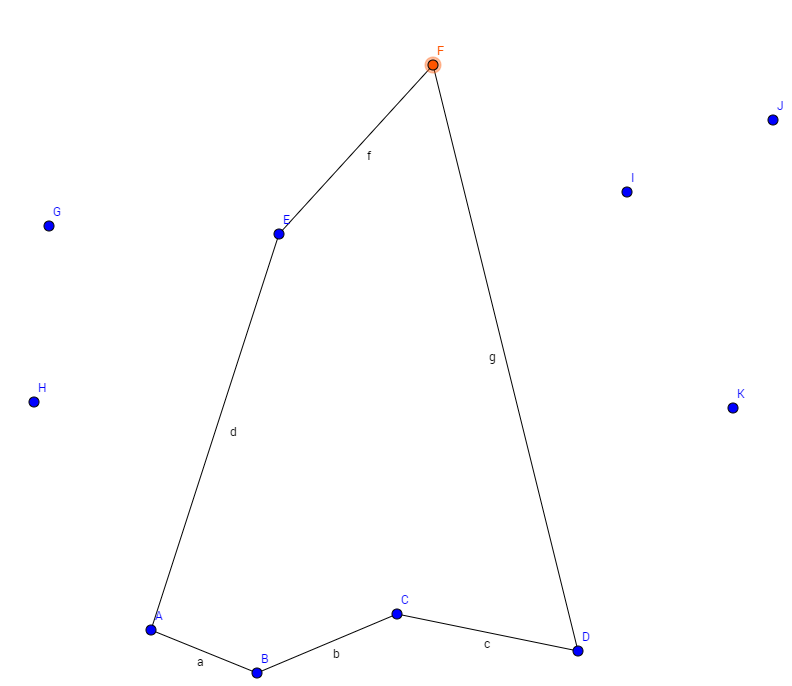
- Auswahl eines beliebigen Knotens
- Hinzufügen des Knoten in bestehende Tour
Komplexität der Heuristik
Die Komplexität die für Random-Insertion wird in der Literatur mit $\mathcal O(n^2)$ angegeben. Somit liegt diese Heuristik ebenfalls in der Komplexitätsklasse P.
Vor- und Nachteile
Im Allgemeinen gelten die gleichen Vor- und Nachteile, wie bei der Nearest-Neighbor-Heuristik, jedoch liefern die Insertion Heuristiken oftmals bessere Lösungen, aufgrund der Tatsache, dass die Suche nicht streng lokal, wie bei Nearest-Neighbor, ist.
Minimum-Spanning-Tree-Heuristik (MST)
gehört zur Gruppe:
Approximationsalgorithmen
Prinzipelles Vorgehen des Verfahrens
Eingabe: Vollständiger bewerteter Graph $K_n$
| Schritt 1: | Bestimmung eines minimal spannenden Baums $B$ in $G$ durch den Algorithmus von Prim oder Algorithmus von Kruskal |
| Schritt 2: | Verdopple jede Kante in $B$ |
| Schritt 3: | Bestimme einen Eulerkreis $K$ in $B$. Der Startknoten ist beliebig. |
| Schritt 4: | Erstelle einen neuen Graphen $K'$. Übernimm dabei alle Kanten aus $K$ und entferne alle Kante, die bereits zu besuchten Knoten führen. Ersetze diese Kante durch eine Kante zum Knoten der im Eulerkreis an nächster Stelle kommt. Ausnahme dabei ist der Startknoten. |
Ergebnis: $Hamilton-Kreis$
Beispiel für ein TSP
Komplexität der Heuristik
Die Komplexität der Heuristik ist polynomiell, da der Algorithmus von Prim bzw Kruskall in Polynomialzeit durchführbar ist.
| Schritt | Komplexität |
|---|---|
1 |
$$\mathcal O (n^2)$$ |
2 |
$$\mathcal O (n)$$ |
3 |
$$\mathcal O (n)$$ |
4 |
$$\mathcal O (n)$$ |
Vor.- und Nachteile
| Vorteile | Nachteile |
|---|---|
| schnelles Verfahren | keine exakte Lösung, da das Gewicht des MST größer als die optimale Rundreise sein kann |
| geeignet für große Problemgrößen | |
| praktikabel | |
| kann ein praktisch unlösbares Problem lösen |
Anwendung in der Praxis
Ein Außendienstmitarbeiter soll alle Kunden die ein bestimmtes Produkt benutzen aufsuchen und ein neues vorstellen. Gesucht ist der kürzestes Weg der alle Kunden beinhaltet.
Ein Mitarbeiter von einem Pflegedienst soll in einem bestimmten Stadtbezirk die Patienten so abfahren das der weg am geringsten ist.
Das bohren von Leiterplatten in der Elektronik. Hier bei sind Leiterbahnen in Platinen geätzt jetzt sollen Löcher so gebohrt werden das der Abstand zwischen bestimmten Bauteilen minimal ist.
In der Automobil Industrie soll ein Schweißroboter so schnell wie möglich festgelegte Schweißnähte an der Karosserie ziehen. Dabei liegt ist es für die Hersteller wichtig, dass der Schweißroboter so wenig wie möglich Weg ohne das Ziehen einer Schweißnaht zurück legt.
Quellen
- Krischke/Röpcke, 2015, Graphen und Netzwerktheorie
- Wagenknecht, 2003, Algorithmen und Komplexität
- Vossen/Witt, 2000 , Grundlagen der Theoretischen Informatik mit Anwendungen
- Schöning, 1992, Theoretische Informatik kurz gefasst
- Hartmann, 2015, Mathematik für Informatiker
- Gumm/Sommer, 2013, Einführung in die Informatik
- [2]