Grundbegriffe der Graphentheorie 1
Aus ProgrammingWiki

Inhaltsverzeichnis |
Relevanz und Motivation
Entstehung von Theorien und Modellen
- Meist aus einem praktischen Problem heraus
- Zusammentragen aller Fakten die damit irgendwie zu tun haben
- Weglassen aller Dinge die keinen direkten Einfluss haben
- Verallgemeinerung / Abstraktion
- Finden von Ähnlichkeiten mit bekannten einfacheren Dingen
- Entwurf eines Modells mit diesen einfacheren Dingen
- Verhältnismäßig einfache Bestimmung von übertragbaren Eigenschaften und Konsequenzen
Leonard Euler 1737
- Problem der Königsberger Brücken
- Weglassen von Entfernungen und Ausmaßen
- Einfluss haben nur Stadtteile und Brücken
- Abstraktion zu Punkten mit Verbindungslinien
- Lösung des Problems mit Punkten und Verbindungen löst auch das Problem mit Stadtteilen und Brücken
- Entstehung des Graphenmodells
Die Graphentheorie als Modell
- Sehr minimalistisch, nur Punkte mit Verbindungen
- Dadurch übertragbar auf alle Arten von Beziehungen zwischen Objekten
- Städte und Zugverbindungen
- Freundschaften zwischen Menschen
- Verlinkung von Internetseiten
- Viele praktische Probleme lassen sich zu einem Graphenproblem umformulieren
- Ausfallwahrscheinlichkeit von Netzwerken
- Routenermittlung bei der Navigation
- Einstufung der Wichtigkeit von Einzelnen in einer Gruppe
- Graphentheorie stellt bereits Lösungen zur Verfügung
- Meist ist "nur noch" eine Interpretation erforderlich
Arbeiten mit dem Graphenmodell
- Mathematik des Modells ist gut dokumentiert
- Kritisch sind die Transformationen
- Formulierung eines praktischen Problems im Graphenmodell
- Interpretation des mathematischen Ergebnisse für die Praxis
- Falsche Formulierung oder falsche Interpretation liefert keine Problemlösung
- Zeitverteilung eines Softwareentwicklers: 10% tippen, 90% denken
- Gute Programmierer denken immer abstrakt (also in Modellen)
- Wenn man viele Modelle kennt, muss man sich selbst keine ausdenken
- Die Einfachheit der Graphentheorie macht sie zu einem Universalmodell
Knoten und Kanten
- Definition Graph
- $\color{red}G=\color{blue}(V,E\color{blue}),~V=\color{green}\{v\color{green}\},~V \color{orange}{\neq \emptyset},~E=\color{green}\{~\color{brown}\{x,y\color{brown}\}~\color{magenta}|~x,y \in V~\color{green}\}$*
- Gelesen: Ein $\color{red}{Graph}$ ist ein $\color{blue}{geordnetes~Paar}$, wobei dessen erstes Element eine $\color{green}{Menge}$ ist, welche $\color{orange}{nicht~leer}$ sein darf, und dessen zweites Element eine $\color{green}{Menge}$ von $\color{brown}{Zweiermengen}$ ist, $\color{magenta}{mit~der~Eigenschaft,~dass}$ die Zweiermengenelemente in der ersten Menge enthalten sein müssen.
- $V$ (für Vertices) ist die Menge der Knoten
- $E$ (für Edges) ist die Menge der Kanten
- Man beachte: Es ist nicht festgelegt, was $v$ eigentlich ist!
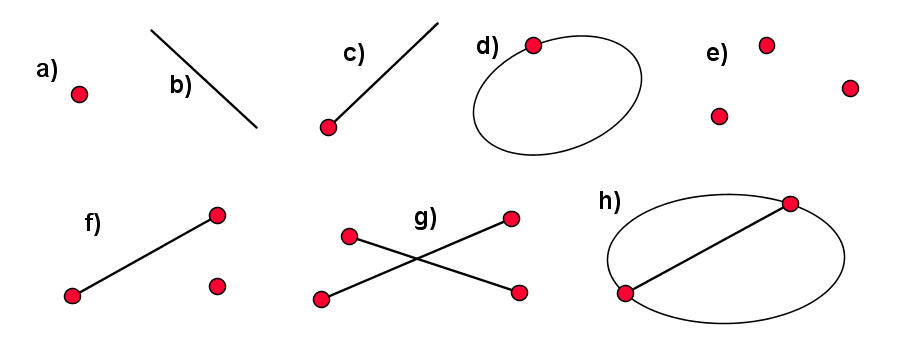
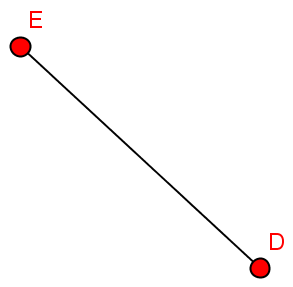
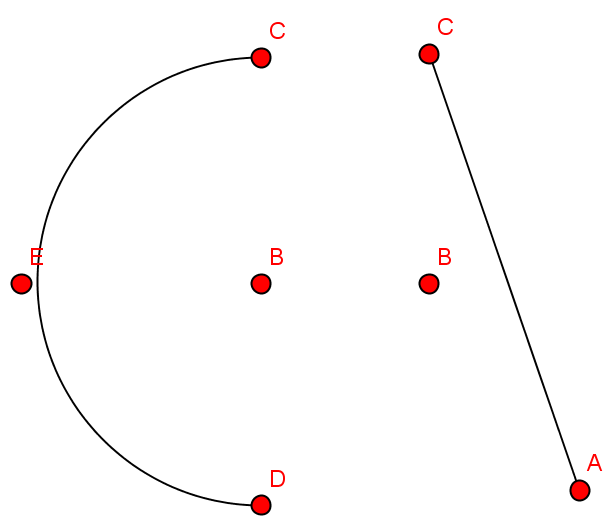
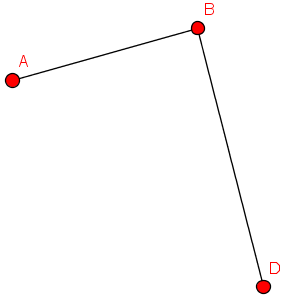
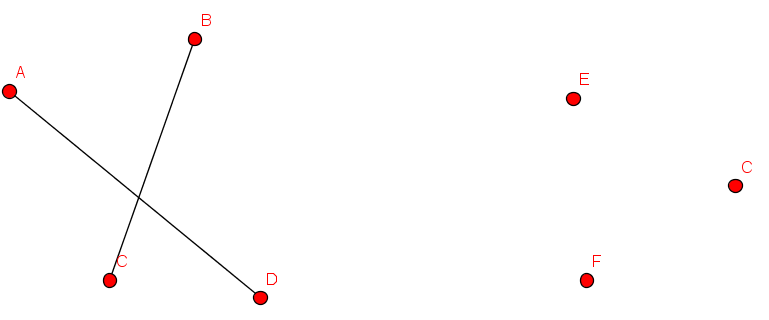
- Zur grafischen Darstellung bieten sich Punkte und Linien an
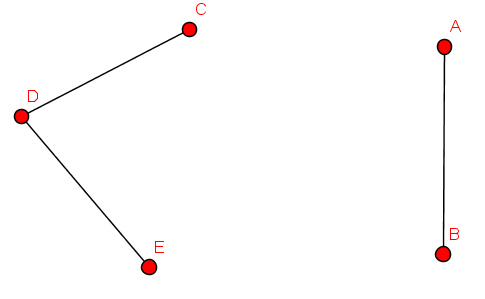
- Welche der Darstellungen repräsentieren Graphen?
Konsequenzen
- Ein Graph muss mindestens einen Knoten enthalten
- Ein Graph muss nicht unbedingt Kanten haben
- Eine Kante muss immer durch 2 (nicht zwingend verschiedene) Knoten begrenzt sein
- Zwei Graphen sind gleich, wenn sie die gleichen Knoten enthalten, die durch die gleichen Kanten verbunden sind
- Adjazenz = Nachbarschaft = Es gibt etwas trennendes dazwischen
- Nur zwischen Knoten und Knoten bzw. zwischen Kante und Kante
- Dazwischen ist immer eine Kante oder ein Knoten
- Inzidenz = Angrenzung = Es gibt direkten Kontakt
- Nur zwischen Knoten und Kante
- $n$ für Anzahl der Knoten
- $m$ für Anzahl der Kanten
In der Praxis
- Knoten und Kanten werden immer als Objekte mit Beziehungen interpretiert
- Dadurch werden die Konsequenzen intuitiv klar
- Erst wenn es ein Objekt gibt, kann man etwas darüber aussagen: "ist allein"
- Zwei Objekte ohne Verbindung sind auch sinnvoll: "nicht allein, aber isoliert"
- Eine Beziehung findet per Definition immer zwischen Objekten statt
- Objekte müssen dabei nicht zwingend verschieden sein (z.B. Besitzer$\leftrightarrow$Eigentümer)
Modellierung
- Transformation einer Gegebenheit/eines Problems ins Graphenmodell
- Scheinbar offensichtlich (Computernetzwerke, Straßen, Facebook-Freundschaften)
- In der Praxis: Immer abhängig von der Problemstellung!
- z.B. Kabelverlegung in einem Haus
- Wie verlegt man die Kabel, sodass die verwendete Gesamtkabellänge minimal ist?
- Wie teile ich eine 50m Kabelrolle auf, sodass der Verschnitt möglichst gering ist?
- Kein Patentrezept um von der konkreten Problemstellung zum abstrakten Graphenmodell zu gelangen
- Hilfreiche Fragen die man sich stellen kann
- Welches Ergebnis wird gebraucht?
- Welches Ergebnis der Graphentheorie soll genutzt werden?
- Oft helfen Zwischen-Abstraktionen anstatt direkt zu Knoten und Kanten zu abstrahieren
- Zustände und deren Übergänge
- Situationen und deren Änderung
- Grafische Darstellung von Graphen kann geometrische Körper ergeben
Programmiertechnische Verarbeitung
- Wie bilde ich das gestellte Problem programmtechnisch ab?
- Mathematische Analyse ($\rightarrow$ mathematische Grundalgorithmus)
- Verbesserung des Algorithmus (dynamic programming, divide & conquer, ...)
- Definition der Datenstruktur zur effizienten Unterstützung des Algorithmus
- Wahl der Datenstruktur immer nach Anforderungen des Algorithmus
- Speicherbedarf vs. Effizienz
Naive Herangehensweise
- Streng nach Definition: Menge von Knoten + Menge von Kanten (zwischen Knoten)
- Kante von a nach b vorhanden? $\mathcal{O}(m)$
- Anzahl anliegender Kanten am Knoten? $\mathcal{O}(m)$
- Speicherbedarf $\mathcal{O}(n+2m)$
Adjazenzmatrix
- Matrix der Größe $n\times n$, 0 oder 1 für jedes Punkte-Paar
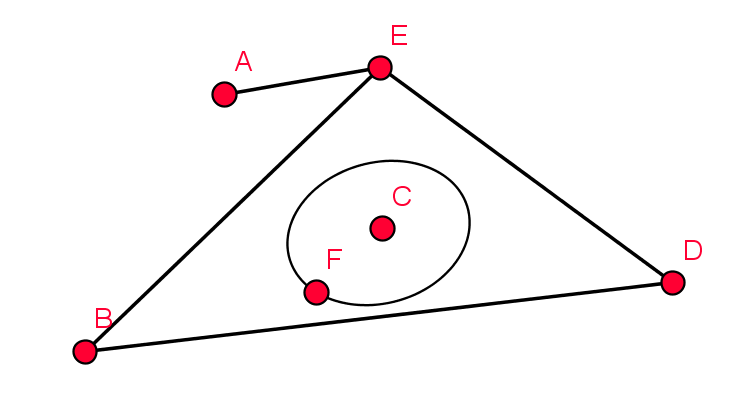
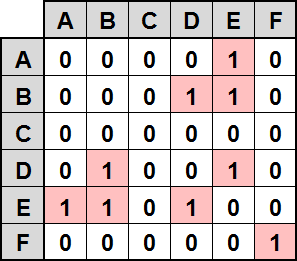
- Kante von a nach b vorhanden? $\mathcal{O}(1)$
- Anzahl anliegender Kanten am Knoten? $\mathcal{O}(n)$
- Speicherbedarf $\mathcal{O}(n^2)$ (oder doch etwas weniger möglich?)
- Codebeispiel:
- Speicherbedarf unabhängig von der Kantenanzahl
- Bei großen Graphen nicht mehr möglich
Adjazenzliste
- Weglassen der Nullen in der Adjazenzmatrix
- Liste der Knoten mit deren Nachbarn

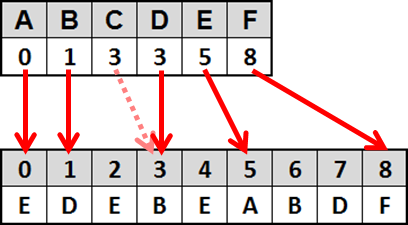
- Kante von a nach b vorhanden? $\mathcal{O}(n)$
- Anzahl anliegender Kanten am Knoten? $\mathcal{O}(1)$
- Speicherbedarf $\mathcal{O}(n+m)$
- Codebeispiel:
- Für jeden Knoten ein neighborIndex wo in neighbors seine adjazenten Knoten abgelegt sind
- Knoten ohne Nachbar erkennbar wenn der Folgeknoten den gleichen neigborIndex hat
Achtung! Sonderbehandlung des letzten Knotens
- Für jeden Knoten ein neighborIndex wo in neighbors seine adjazenten Knoten abgelegt sind
- weniger Speicherbedarf als Adjazenzmatrix wenn Graph nicht vollständig
Kantenliste
- Nur die Kanten (zwischen 2 Knoten) werden gehalten


- Kante von a nach b vorhanden? $\mathcal{O}(m)$
- Anzahl anliegender Kanten am Knoten? $\mathcal{O}(m)$
- Speicherbedarf $\mathcal{O}(m)$
- Codebeispiel:
- Speicherbedarf unabhängig von der Knotenanzahl
- keine Unterstützung isolierter Knoten
In der Praxis
- Knoten und Kanten sind meist komplexere Datenstrukturen (beliebige Klassen)
- Bei Algorithmenimplementation generics bzw. templates benutzen
- Hilfsdatenstrukturen richtig verwenden (HashMap, HashSet)
- Redundanz vermeiden (Speicherbedarf minimieren), oder auch explizit nutzen (Effizienzsteigerung)
Grad eines Knotens
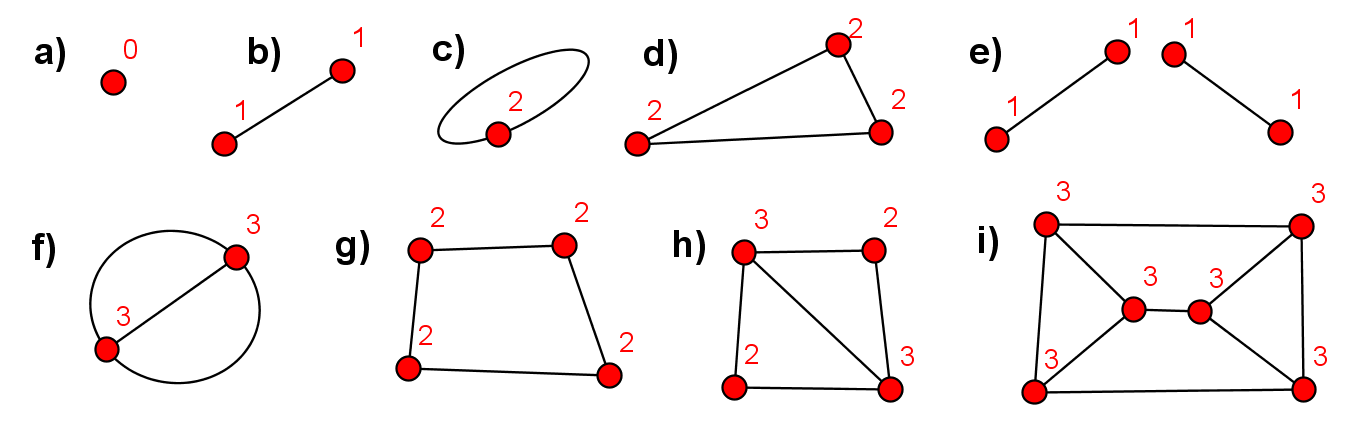
- Definition
- $\color{red}d(\color{orange}v) = \color{blue}|~\color{green}\{~\color{brown}\{\color{orange}v,x\color{brown}\}~\color{magenta}{|~\{v,x\} \in E}~\color{green}\}~\color{blue}|$*
- Gelesen: Der $\color{red}{Grad}$ eines $\color{orange}{Knotens}$ ist die $\color{blue}{Kardinalität}$ der $\color{green}{Menge}$ von $\color{brown}{Zweiermengen}$, die diesen $\color{orange}{Knoten}$ enthalten und $\color{magenta}{in~E~enthalten~sind}$.
- Einzelner Knoten ohne anliegende Kanten hat Grad 0 (isolierter Knoten)
- Schleife an einem Knoten erhöht den Grad um 2
- Haben alle Knoten den gleichen Grad ist der Graph regulär
genauer: bei Grad k $\rightarrow$ k-regulär - Stark regulär:
- 2 benachbarte Knoten haben immer gleich viele gemeinsame Nachbarknoten und
- 2 nicht benachbarte Knoten haben immer gleich viele gemeinsame Nachbarknoten
- Ein Graph hat: Minimalgrad, Maximalgrad, Durchschnittsgrad
- Wichtig: $\sum_{i=1}^n d(v_i)=2\cdot m$
- Summe aller Grade entspricht doppelter Kantenanzahl im Graph
- Da jede Kante den Grad ihrer 2 angrenzenden Knoten um 1 erhöht
- Daraus folgt: Anzahl der Knoten mit ungeradem Grad muss gerade sein
- Praktisch: schnelle Überprüfbarkeit einer Aussage
Unter 7 Unternehmen unterhält jedes Geschäftsbeziehungen zu genau 3 anderen Unternehmen. Möglich?
Isomorphie
- Gleichstrukturiertheit von Graphen $G \sim G'$
- Grafische Darstellung der Graphen kann ineinander überführt werden (Morphing)
- Achtung: Isomorphie $<>$ Gleichheit
- Knotennamen für Isomorphie irrelevant
- Ebenso Kantenbewertungen
- Aber: Kantenrichtungen dürfen nicht ignoriert werden
- Algorithmische Prüfung auf Isomorphie ($\mathcal{O}$ per Adjazenzmatrix)
- Anzahl der Knoten muss gleich sein $=\mathcal{O}(1)$
- Anzahl der Kanten bzw. Summe der Grade muss gleich sein $=\mathcal{O}(n^2)$
- Das reicht aber noch nicht!
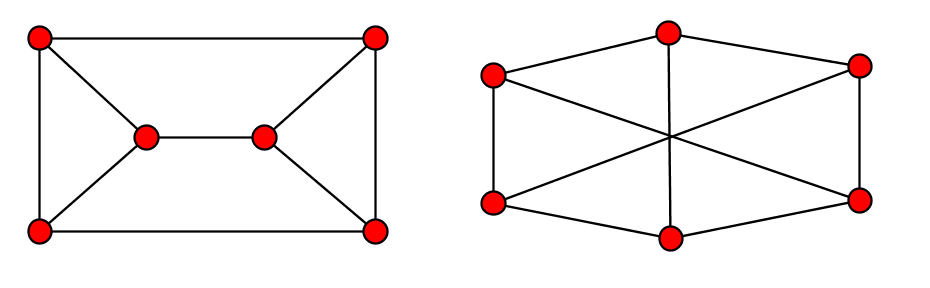
- Die Adjazenzmatrix muss gleich sein von mindestens einer ihrer Permutationen $=\mathcal{O}(n!)$
- Optimierung lt. Ullmann: Partitionieren! (Gruppierung von Knoten mit gleichem Grad)
Dadurch statt $9!=362.880$ Möglichkeiten, Einschränkung auf z.B. $2!\cdot 7!=10.080$ Möglichkeiten - Hier gibts einen Ferrari zu holen...
Kantenzug, Wege, Kreise und Zusammenhang
Kantenzug
- Definition Kantenzug
Für n ≥ 2 nennt man einen Graphen $P_n$ mit einer Folge von Knoten $V(P_n)$ = ($v_0$, $v_1$, . . . , $v_n$) und einer Folge von Kanten $E(P_n)$ = ({$v_0$, $v_1$}, {$v_1$, $v_2$}, . . . , {$v_{n−1}$, $v_n$}) einen Kantenzug der Länge $n$.
Also: Knoten und Kanten können mehrfach durchlaufen werden.
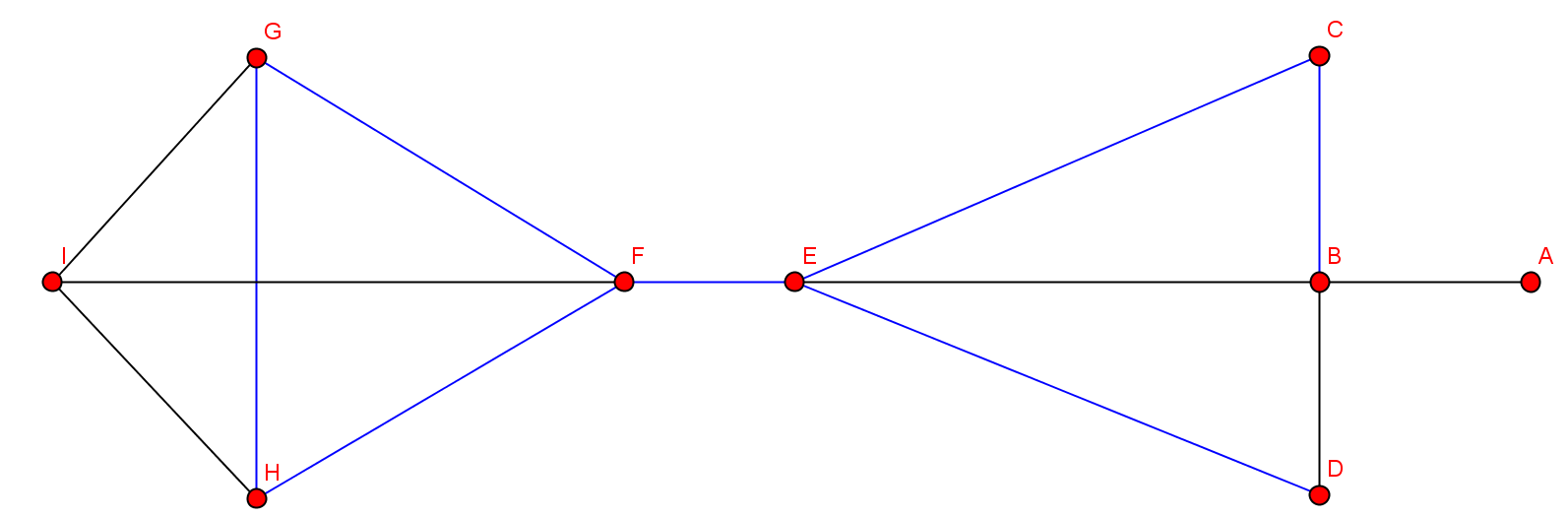
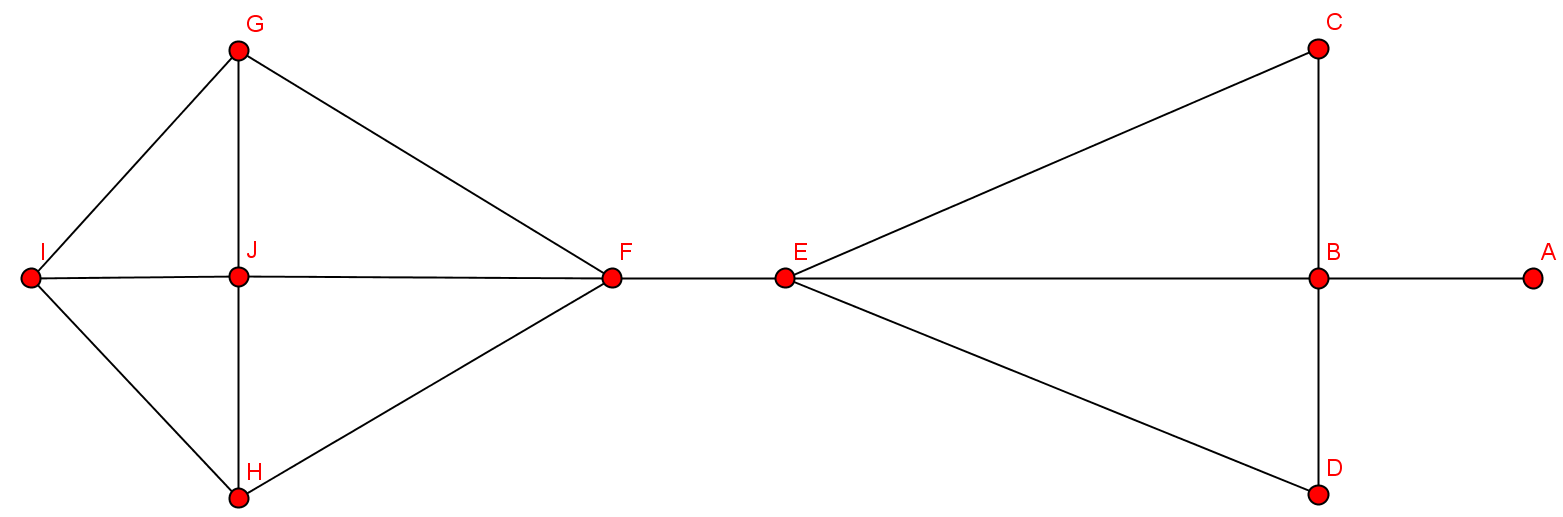
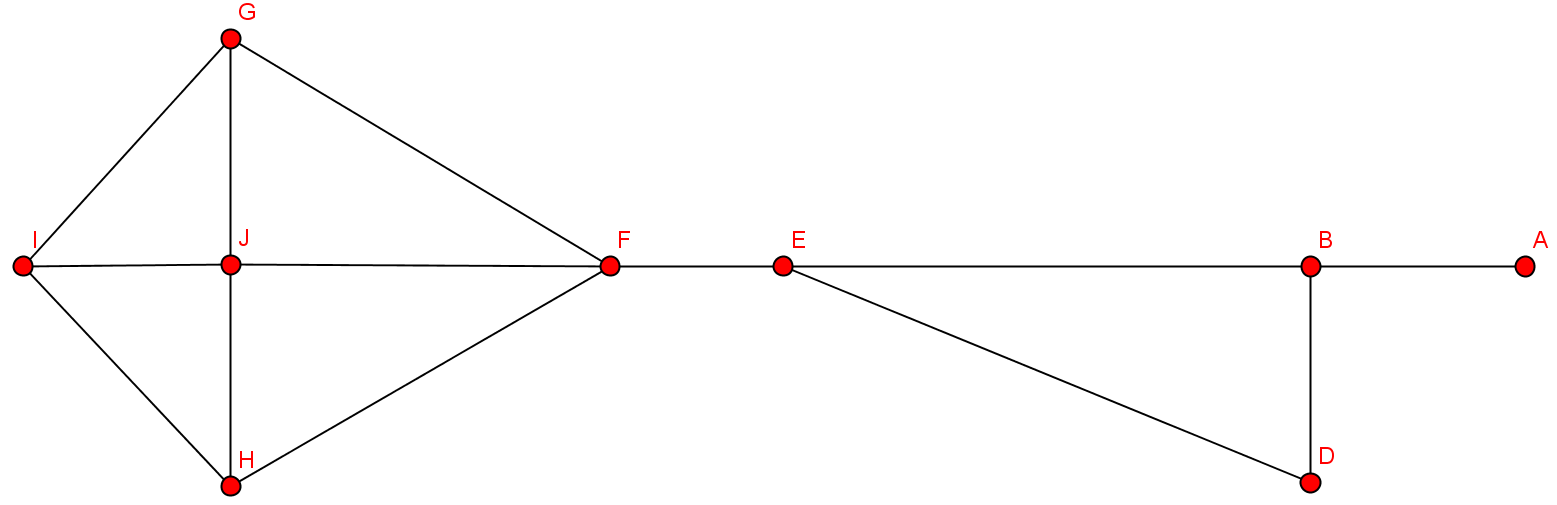
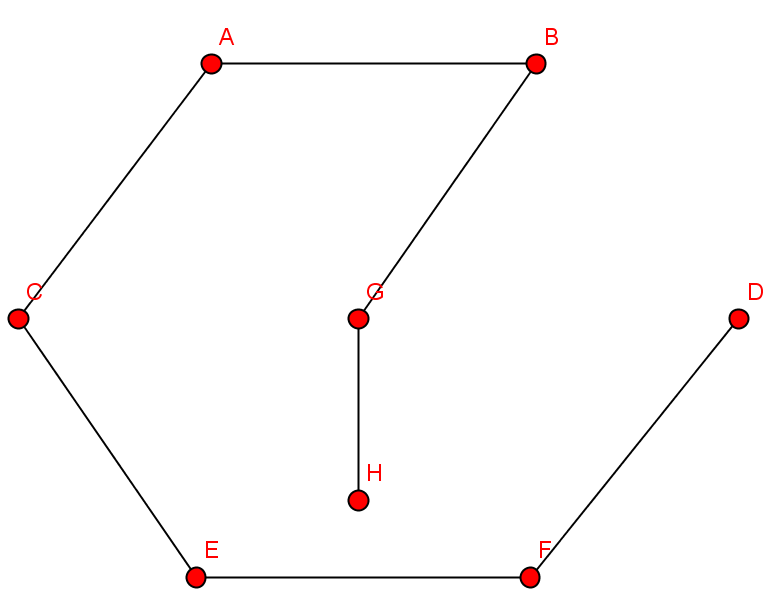
- Kantenzug: {B,C,E,F,G,H,F,E,D}
- Definition Geschlossener Kantenzug
Ein geschlossener Kantenzug ist ein Kantenzug mit $v_0$ = $v_n$.
- Geschlossener Kantenzug: {B,C,E,F,G,H,F,E,D,B}
Weg
- Definition Weg
Für n ≥ 2 nennt man einen Graphen $P_n$ mit der Knotenmenge $V(P_n)$ = {$v_0$, $v_1$, . . . , $v_n$} oder auch einer Folge von Knoten $V(P_n)$ = ($v_0$, $v_1$, . . . , $v_n$) und der Kantenmenge $E(P_n)$ = {{$v_0$, $v_1$}, {$v_1$, $v_2$}, . . . , {$v_{n−1}$, $v_n$}} einen Weg (oder Pfad) der Länge $n$, sofern keine Kante mehrfach durchlaufen wird. Knoten hingegen dürfen bei einem Weg mehrfach vorkommen.
Also: Bei einem Weg dürfen die Knoten mehrfach und die Kanten nur einmal durchlaufen werden.
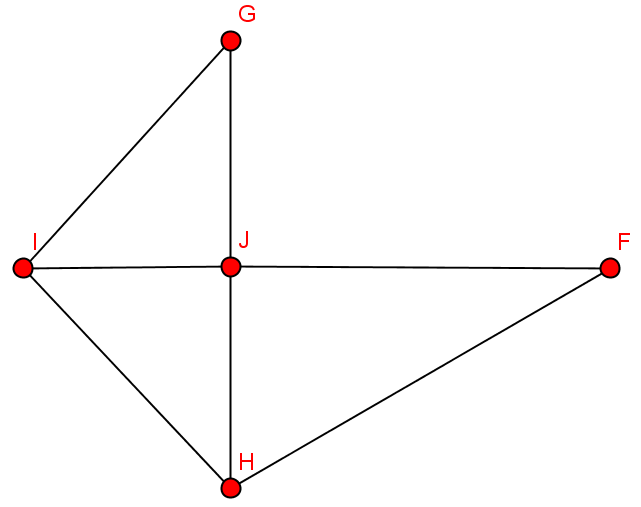
- Weg: {C,E,F,G,J,F}
- Definition Einfacher Weg
Für n ≥ 2 nennt man einen Graphen $P_n$ mit der Knotenmenge $V(P_n)$ = {$v_0$, $v_1$, . . . , $v_n$} und der Kantenmenge $E(P_n)$ = {{$v_0$, $v_1$}, {$v_1$, $v_2$}, . . . , {$v_{n−1}$, $v_n$}} einen einfachen Weg der Länge $n$, sofern keine Kante und kein Knoten mehrfach durchlaufen wird.
Also: Bei einem einfachen Weg dürfen die Knoten und Kanten nur einmal durchlaufen werden.
- Einfacher Weg: {C,E,F,G}
Kreise
- Definition Kreis
Für n ≥3 heißt der Graph $C_n$ mit $V(P_n)$ = {$v_0$, $v_1$, . . . , $v_n$}, oder auch $V(P_n)$ = ($v_0$, $v_1$, . . . , $v_n$), und $E(C_n)$ = {{$v_0$, $v_1$}, {$v_1$, $v_2$}, . . . , {$v_{n−1}$, $v_n$}} Kreis der Länge $n$.
Also: Ein Kreis ist ein geschlossener Weg mit $v_o = v_n$, mit mindestens drei Knoten.
- Kreis: {F,G,J,I,H,J,F}
- Definition Einfacher Kreis
Für n ≥ 3 nennt man einen Graphen $P_n$ mit der Knotenmenge $V(P_n)$ = {$v_0$, $v_1$, . . . , $v_n$} und der Kantenmenge $E(C_n)$ = {{$v_0$, $v_1$}, {$v_1$, $v_2$}, . . . , {$v_{n−1}$, $v_n$}} einen einfachen Weg (oder Pfad) der Länge $n$, sofern keine Kante und kein Knoten mehrfach durchlaufen wird.
Also: Ein einfacher Kreis ist ein geschlossener einfacher Weg mit $v_o = v_n$, mit mindestens drei Knoten.
- Einfacher Kreis: {F,G,J,F}
Zusammenhang bei Graphen
- Definition
Ein Graph ist zusammenhängend, falls es zu je zwei verschiedenen Knoten $v,w∈V(G)$ einen Weg auf $G$ mit $v$ und $w$ als Endknoten gibt. Ein maximal zusammenhängender Teilgraph von $G$ heißt Zusammenhangskomponente von $G$.
Übung
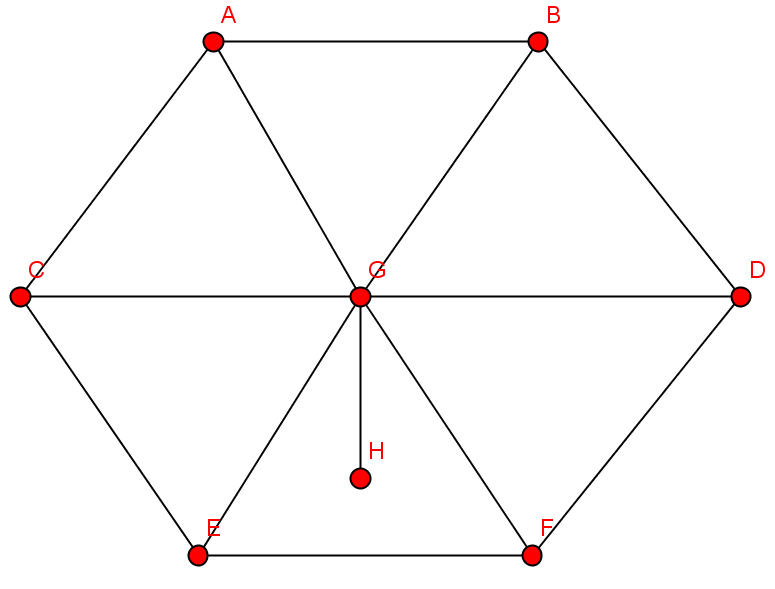
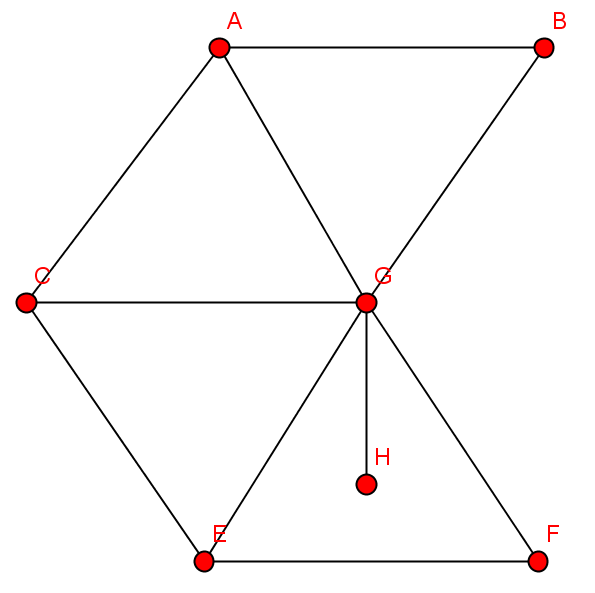
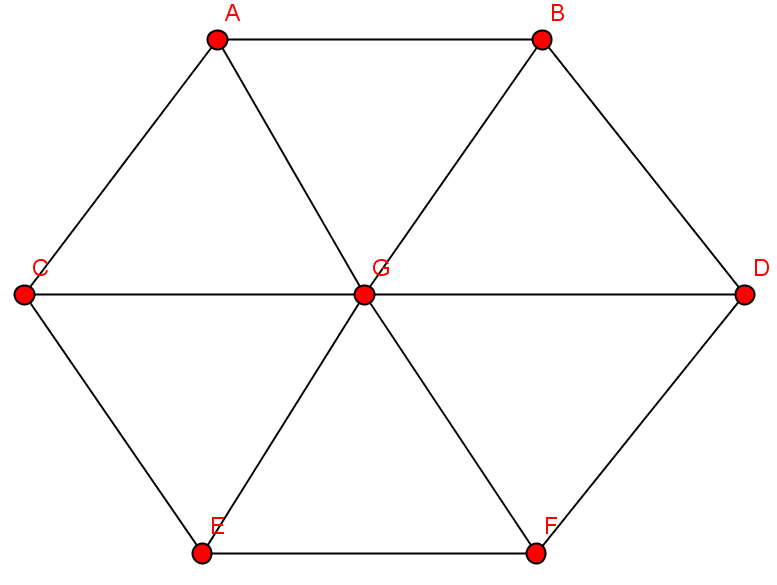
| Knoten | Kantenzug | geschlossener Kantenzug | einfacher Weg | Weg | einfacher Kreis | Kreis |
|---|---|---|---|---|---|---|
| {G,C,A,G,F,E,G} | ||||||
| {G,H} | ||||||
| {D,G,B,D,F,G,B,A} | ||||||
| {G,B,A,G,H} | ||||||
| {A,B,D,G,A} | ||||||
| {G,B,A,G,B,A,G} |
Strukturelle Umformungen
Entfernen von Knoten und Kanten
- Obergraph
- Definition Enfernen von Kanten
Es sei $G = (V,E)$ ein Graph. Das Entfernen einer Kante $e ∈ E$ erzeugt aus $G$ einen neuen Graphen $G - e = (V,E~$\$~,\{e\})$. Wenn $F ∈ E$ eine Kantenteilmenge des Graphen $G = (V,E)$ ist, so sei $G - F$ der Graph, der aus $G$ durch Entfernen aller Kanten aus $F$ hervorgeht.
Also: Entfernung einer Kante -> neuer Graph bzw. Graphen
- Definition Enfernen von Knoten
Als einen Knoten $v ∈ V$ wird $G - v$ als der Graph definiert, der aus $G$ durch Entfernen des Knotens $v$ hervorgeht. Das Entfernen eines Knotens $v$ schließt hierbei das gleichzeitige Entfernen aller zu $v$ inzidenten Kanten des Graphen ein.
Also: Entfernung eines Knoten -> neuer Graph, hierbei das gleichzeitige Entfernen aller zum Knoten inzidenten Kanten.
Kontraktion
- Definition Kontraktion
Die Kontraktion einer Kante $e = \{u,v\}$ eines Graphen $G$ ist das Entfernen von $e$ mit der anschließenden Fusion der Endknoten $u$ und $v$.
- dadurch Wegverkürzung
- wenn Endknoten = Endknoten des Weges -> Weglänge = 0
- wenn die Kante nicht auf dem Weg liegt, dann bleibt der Weg erhalten
- Folge: Ein Graph ist genau dann zusammenhängend, wenn durch eine Folge von Kontraktionen nur ein Knoten übrig bleibt.
- Obergraph
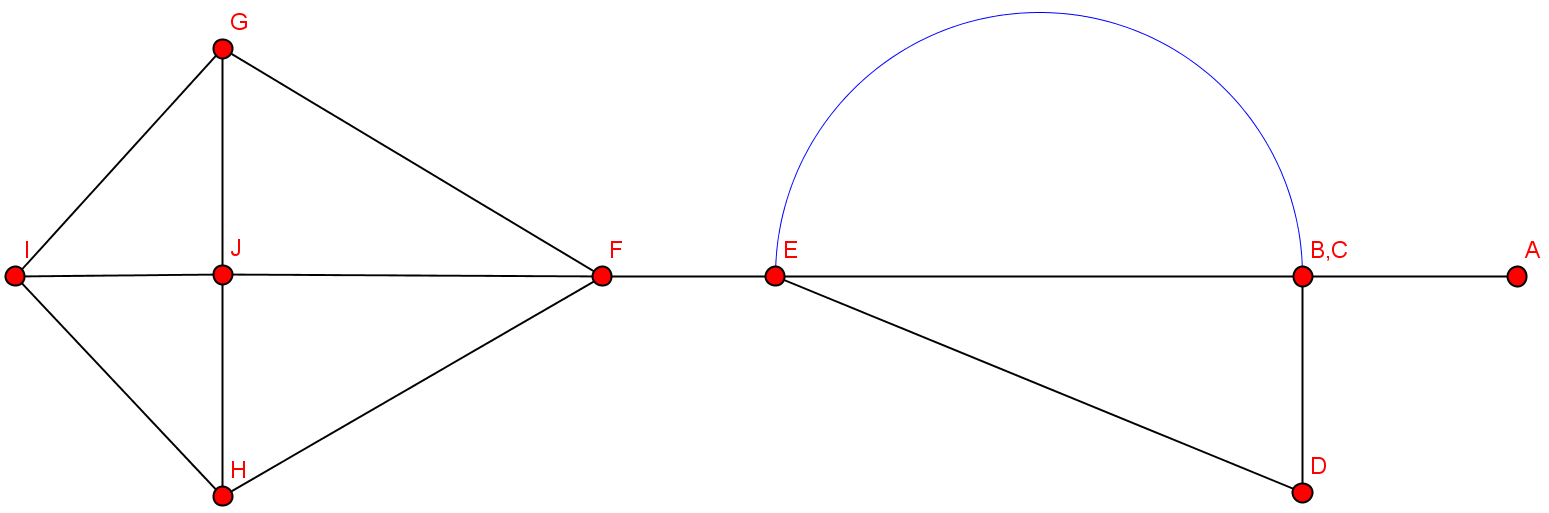
- Nach Kontraktion
Artikulationen (= Knoten)
- Definition
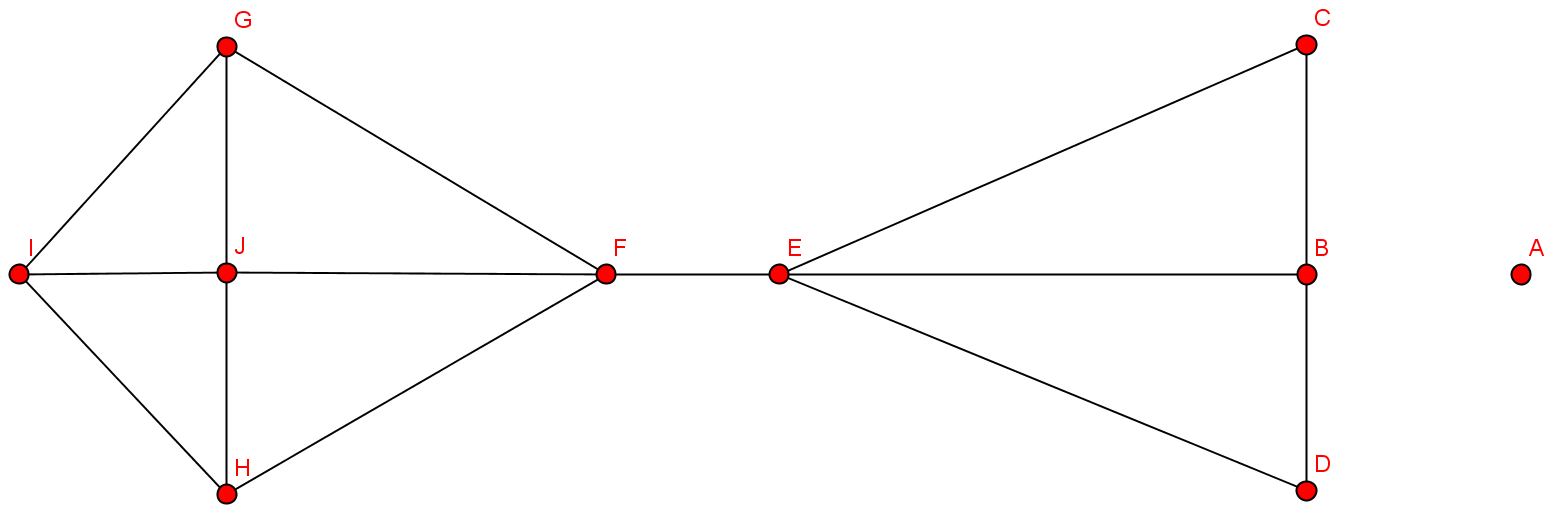
Es sei $c(G)$ die Anzahl der Zusammenhangskomponenten eines Graphen $G$. Ein Knoten $v ∈ V$ mit der Eigenschaft $c(G-v) > c(G)$ heißt eine Artikulation von $G$.
Also: Wenn durch Entfernung eines Knotens der Graph in zwei oder mehrere Zusammenhangskomponenten zerfällt.
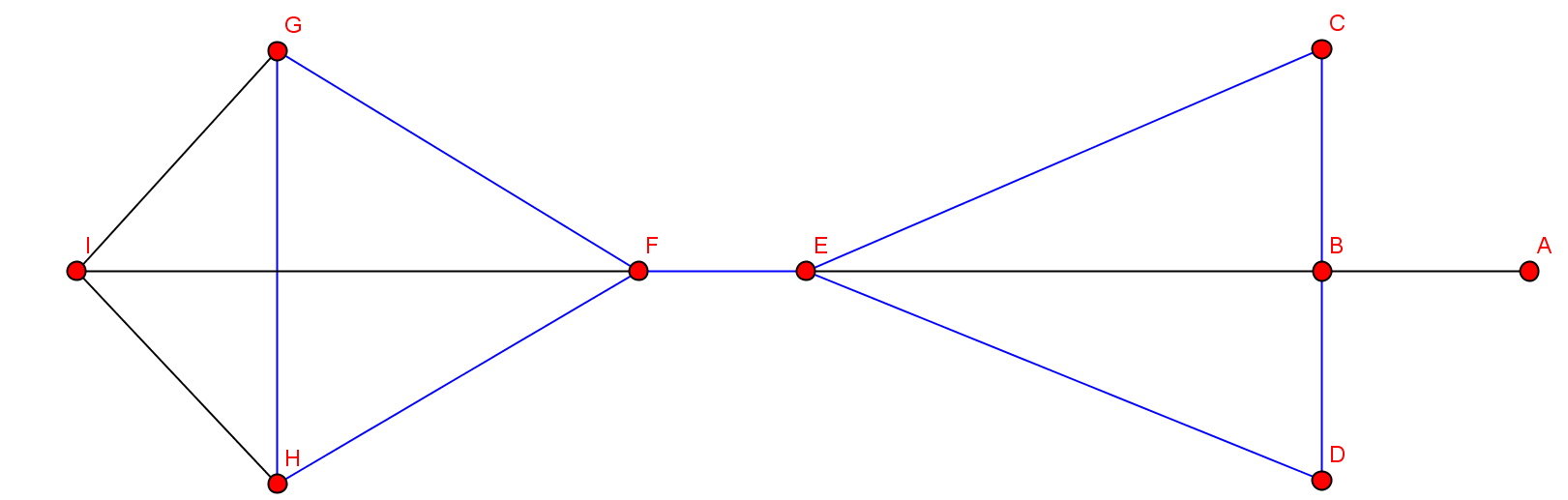
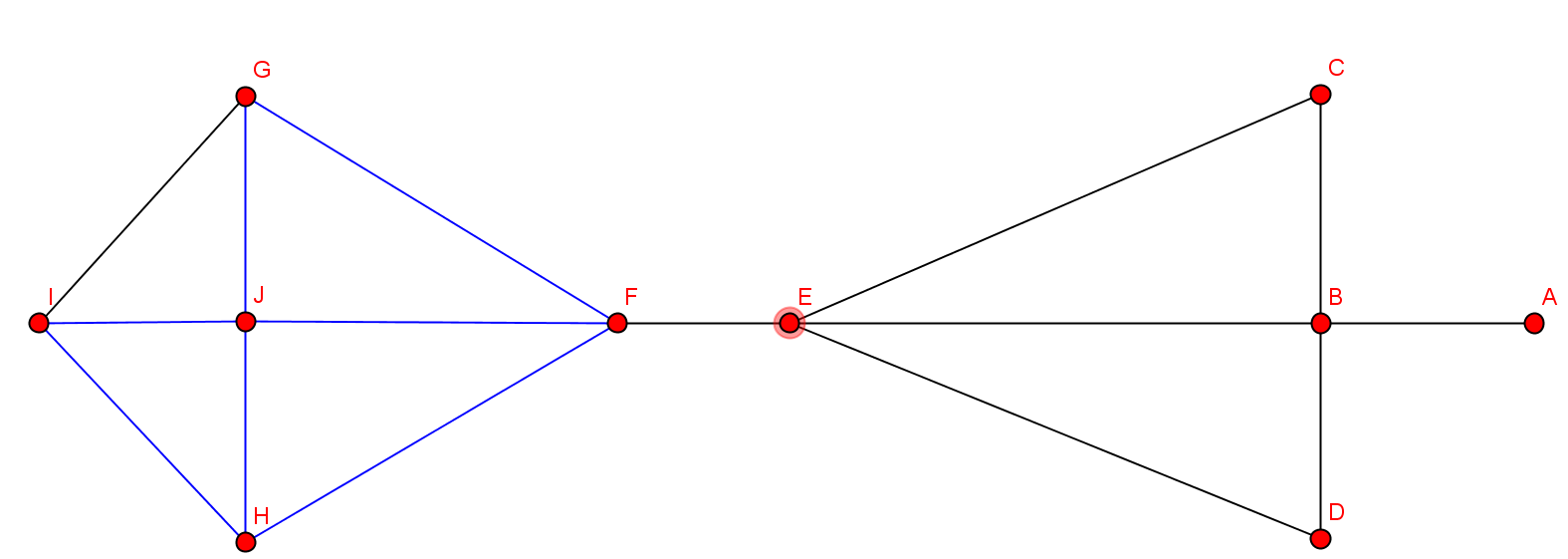
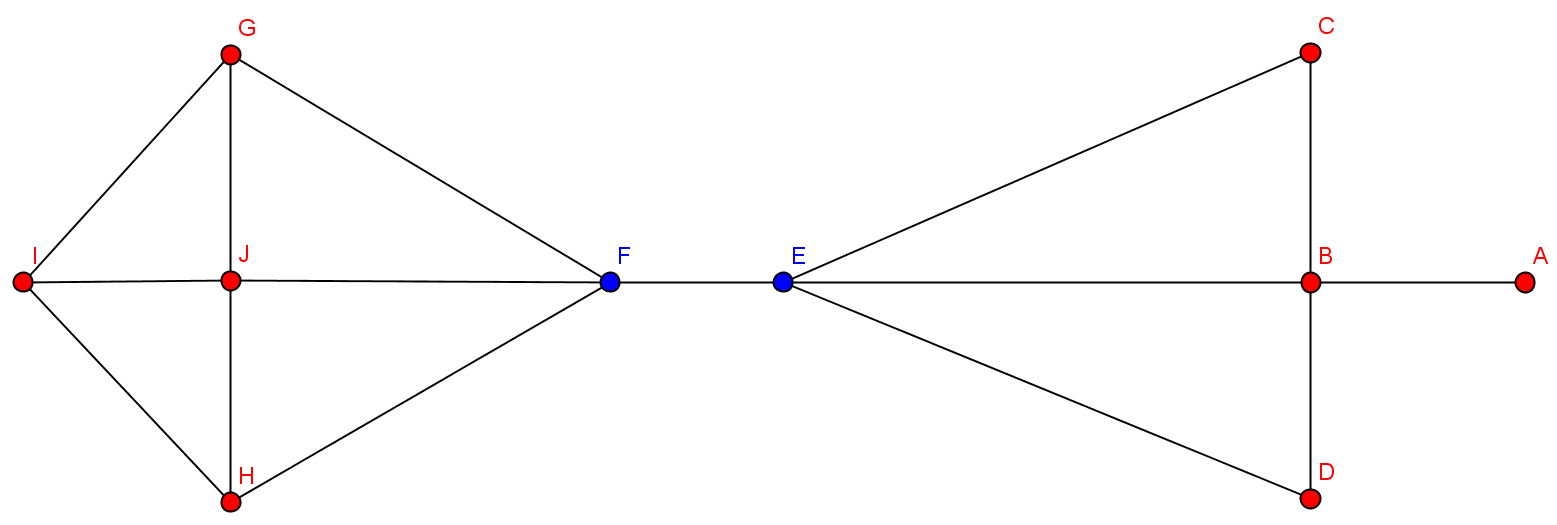
- Kritische Knoten: blau
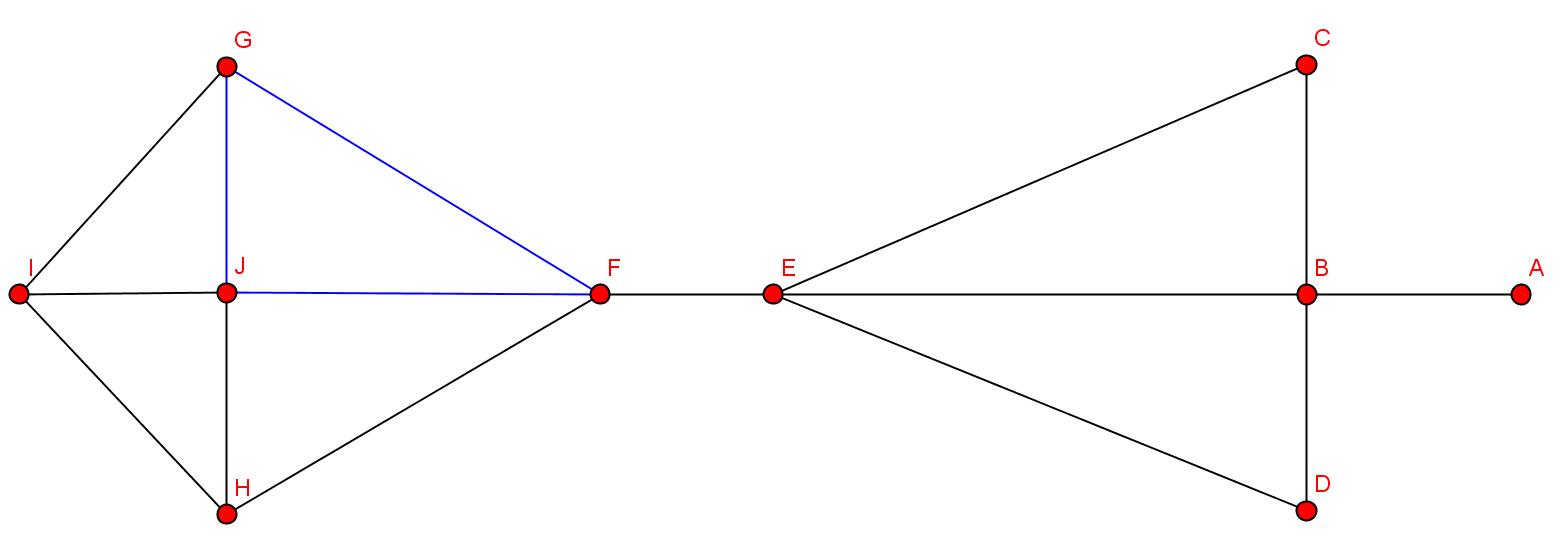
- Nach Entfernung der kritischen Knoten
Brücken (= Kanten)
- Definition
Es sei $c(G)$ die Anzahl der Zusammenhangskomponenten eines Graphen $G$. Eine Kante $e ∈ E$ eines Graphen $G = (V,E)$ mit der Eigenschaft $c(G-e) > c(G)$ heißt eine Brücke von $G$.
Also: Wenn durch Entfernung einer Kante der Graph in zwei oder mehrere Zusammenhangskomponenten zerfällt.
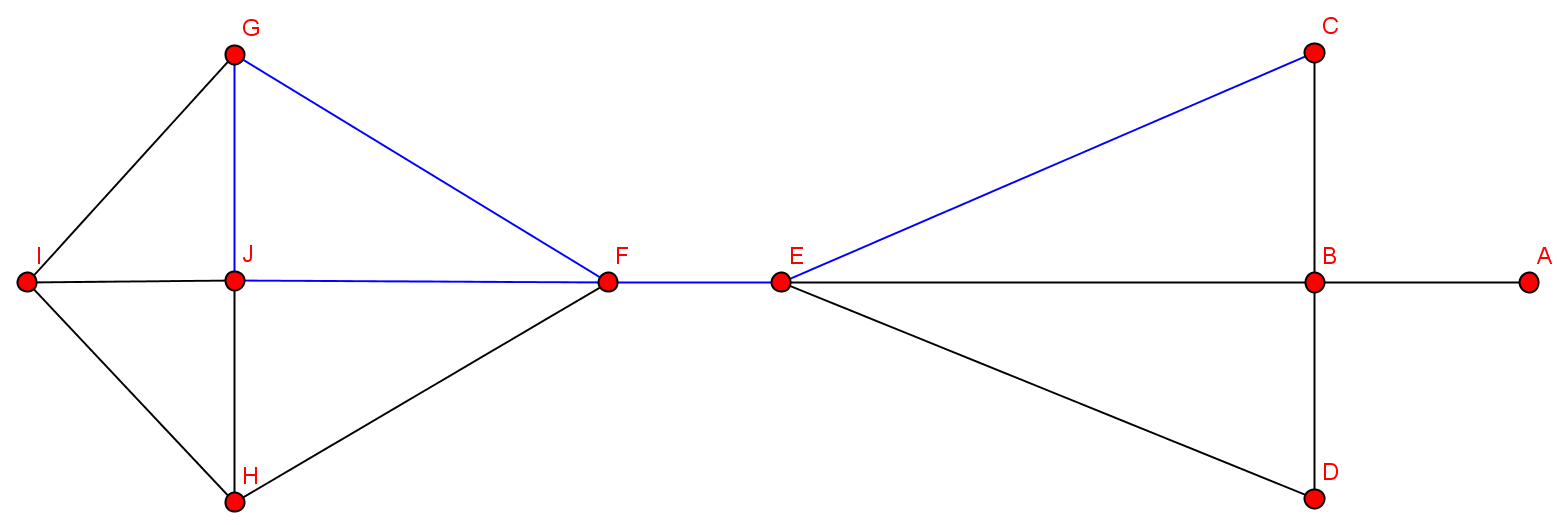
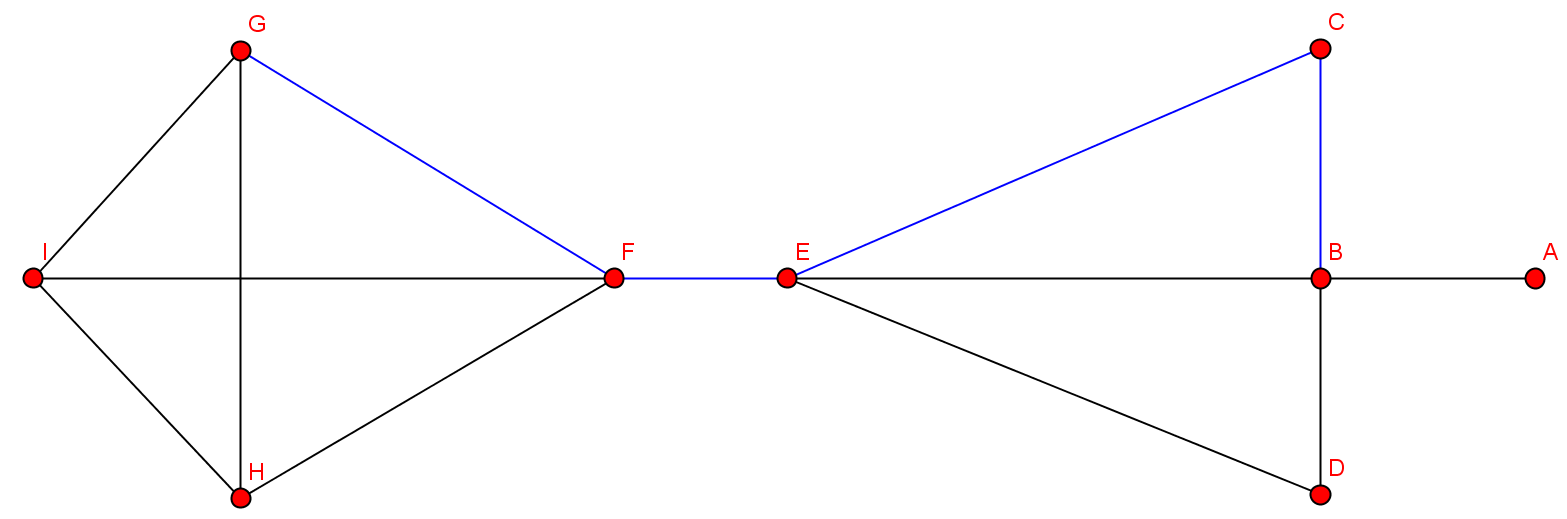
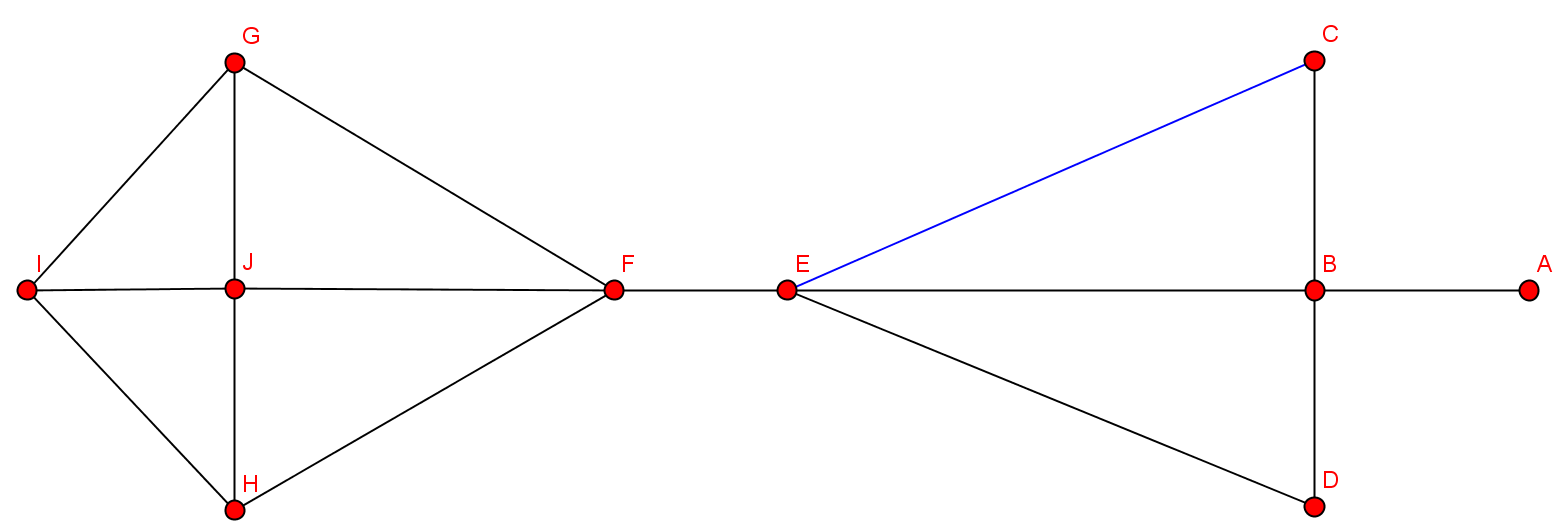
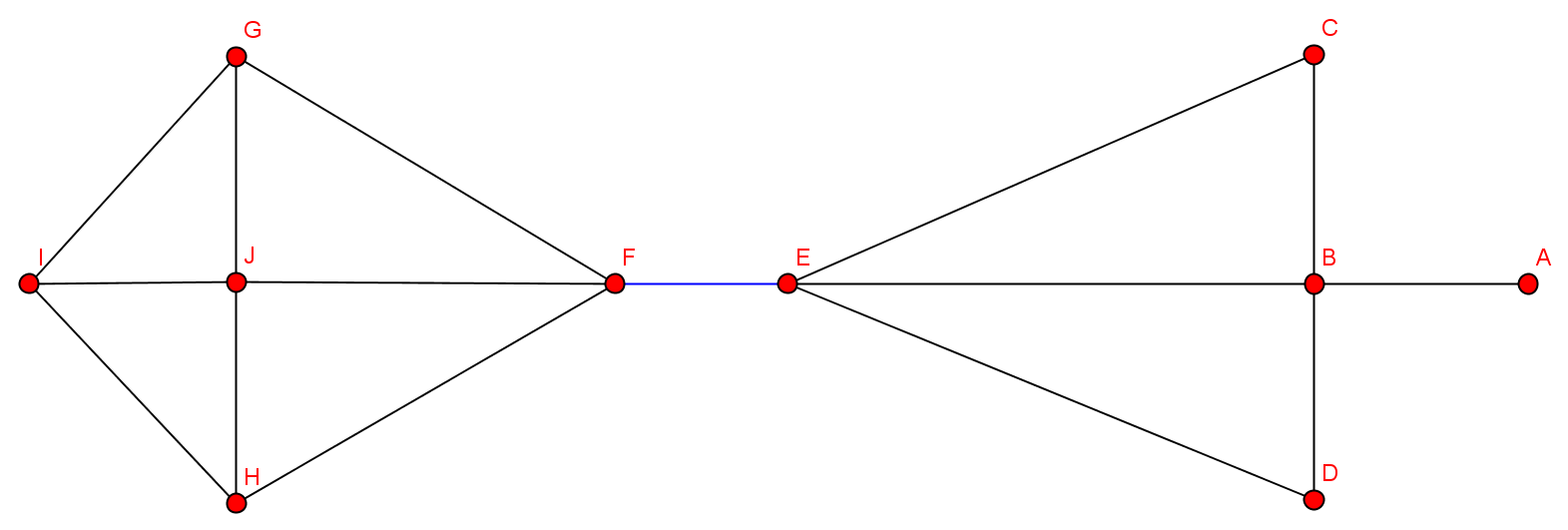
- kritische Kante: blau
- Nach Entfernung der Brücke
Übung
- Was passiert bei Entfernung einer Kante bzw. Knoten
- Was passiert bei Kontraktion?
- Wo ist die Artikulation?
- Wo ist die Brücke?
Vollständige Graphen
- Definition
Ein Graph, bei dem je zwei Knoten benachbart sind, heißt vollständig.
Also: Alle Knoten sind miteinander verbunden
Teilgraph und Untergraph
Teilgraph
- Definition
Es sei $G = (V_G,E_G)$ ein Graph. Ein Teilgraph von $G$ ist ein Graph $H = (V_H,E_H)$, dessen Knotenmenge $E_H\subseteq E_G$ ist.
Also: Ein Teilgraph ist ein Ausschnitt aus einem Graphen, bei der Kanten zwischen den Knoten fehlen können.
- Jeder Untergraph ist auch ein Teilgraph, aber nicht umgekehrt!
induzierter Teilgraph = Untergraph
Ein induzierter Teilgraph entsteht, wenn beim Obergraphen ein oder mehrere Knoten samt dessen inzidenten Kanten entfernt werden.
Untergraph
Ein Untergraph ist ein Ausschnitt aus einem Graphen, dessen Knoten samt dessen inzidenten Kanten erhalten bleiben. Ein Untergraph wird auch als Clique bezeichnet.
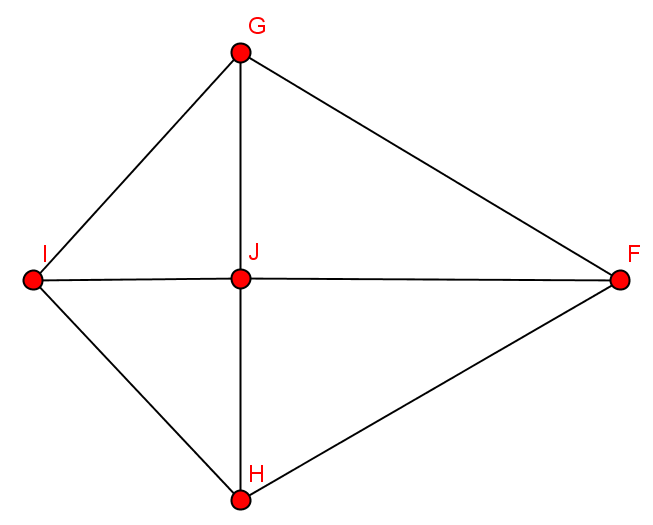
spannender Teilgraph
Beim spannenden Teilgraphen bleiben alle Knoten des Obergraphen erhalten. Die Knoten sind dabei zusammenhängend.
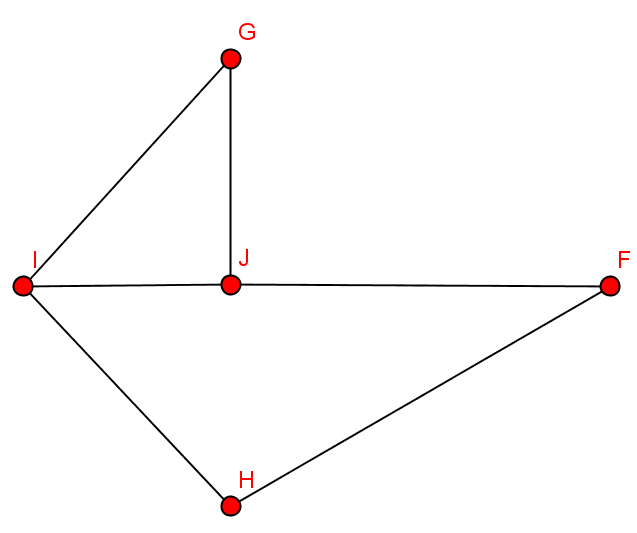
Übung
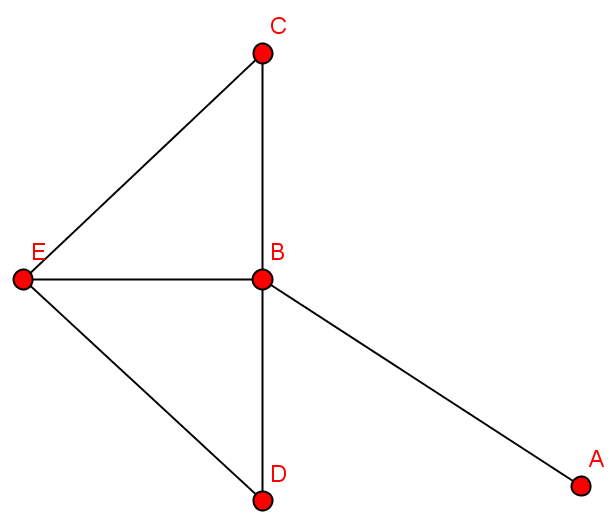
Welche Untergraphen gibt es?
Welche Teilgraphen gibt es?
Skizziere induzierte Teilgraphen!
Wie sieht der spannende Teilgraph aus?
Grundlegende Graphenoperationen
Besonders häufig werden die üblichen Operationen der Mengenlehre (Vereinigung, Durchschnitt, Differenz und Komplement) auf Knoten- bzw. Kantenmengen von Graphen angewendet.
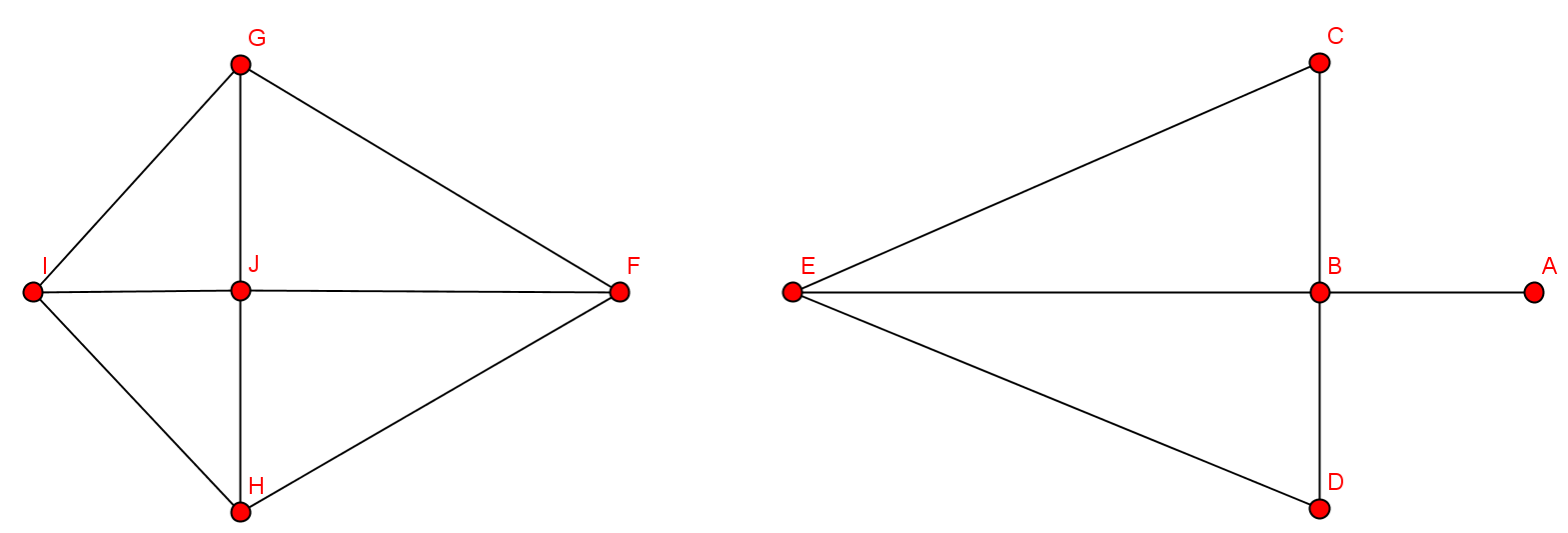
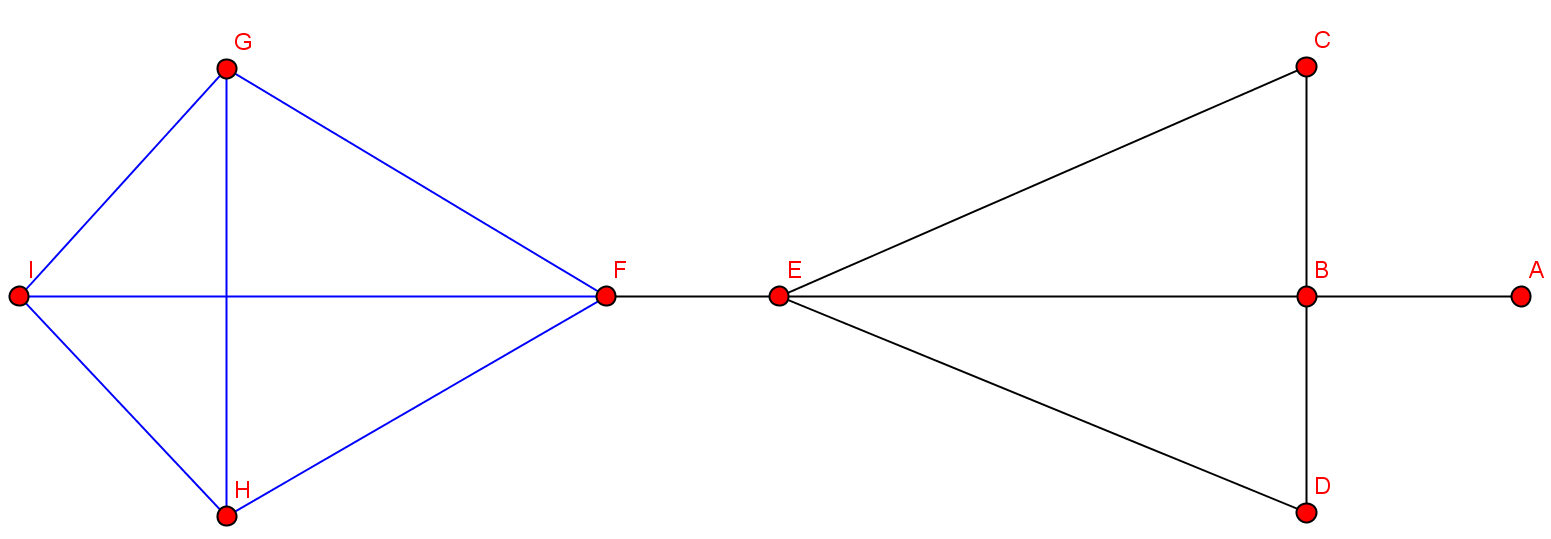
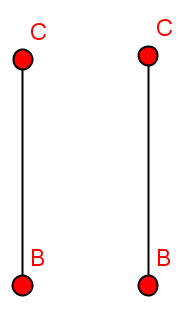
Operation: Durchschnitt
$G\cap G' = V(G)\cap V(G'), E(G)\cap E(G')$, wenn es Knoten und Kanten von $G$ und $G'$ gibt, die übereinstimmen.
Also: Es bleiben nur die Knoten und Kanten erhalten, welche beide Graphen enthalten.
Operation: Vereinigung
$G\cup G' = V(G)\cup V(G'), E(G)\cup E(G')$, wenn es Knoten und Kanten von $G$ und $G'$ gibt, die übereinstimmen.
Also: Zwei Graphen werden durch gleichen Knoten und Kanten vereinigt.
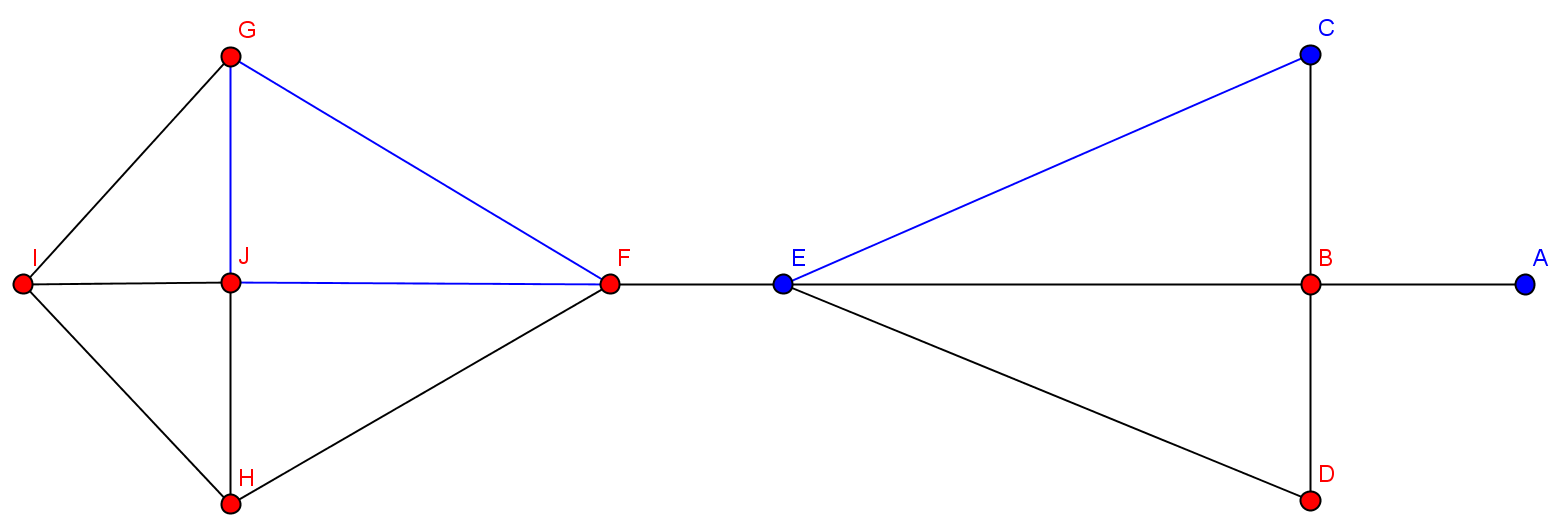
Operation: Differenz
$G\backslash G' = V(G)\backslash V(G'), E(G)\backslash E(G')$
Also: Es bleiben die Knoten und Kanten erhalten, welche nur $G$ besitzt.
Operation: Komplement
Der Komplementärgraph $\overline{G}$ eines Graphen $G$ hat die selbe Knotenmenge wie der Ausgangsgraph. In $\overline{G}$ sind genau zwei Knoten adjazent, wenn sie in $G$ nicht adjazent sind.
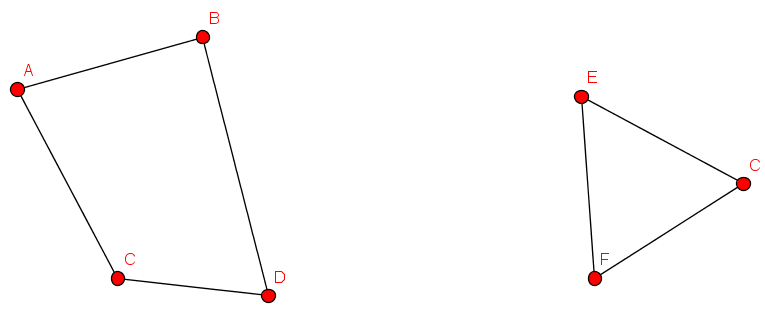
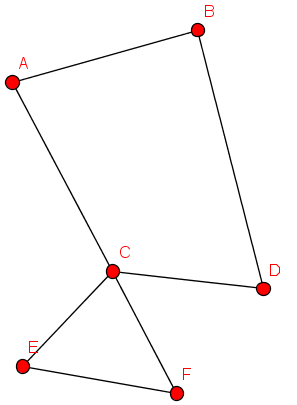
Übung
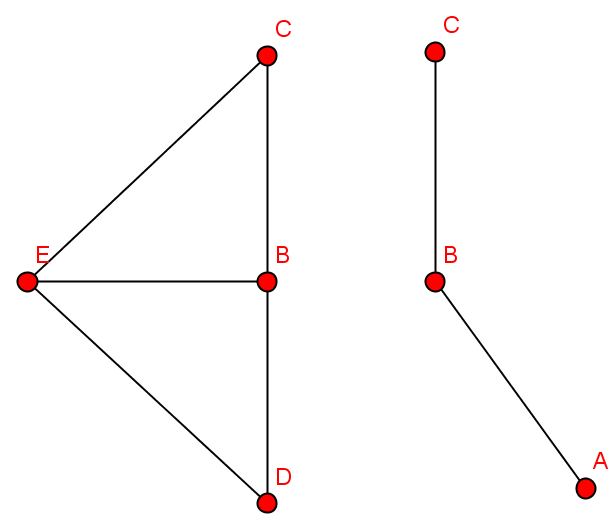
Welcher Graph entsteht durch die Bildung des Durchschnitts?
Welcher Graph entsteht durch Vereinigung?
Welcher Graph entsteht durch Differenz?
Wie sehen die komplementären Graphen aus?
Quellen
- Turau, 2009, Algorithmische Graphentheorie
- Krischke/Röpcke, 2015, Graphen und Netzwerktheorie
- Tittmann, 2003, Graphentheorie