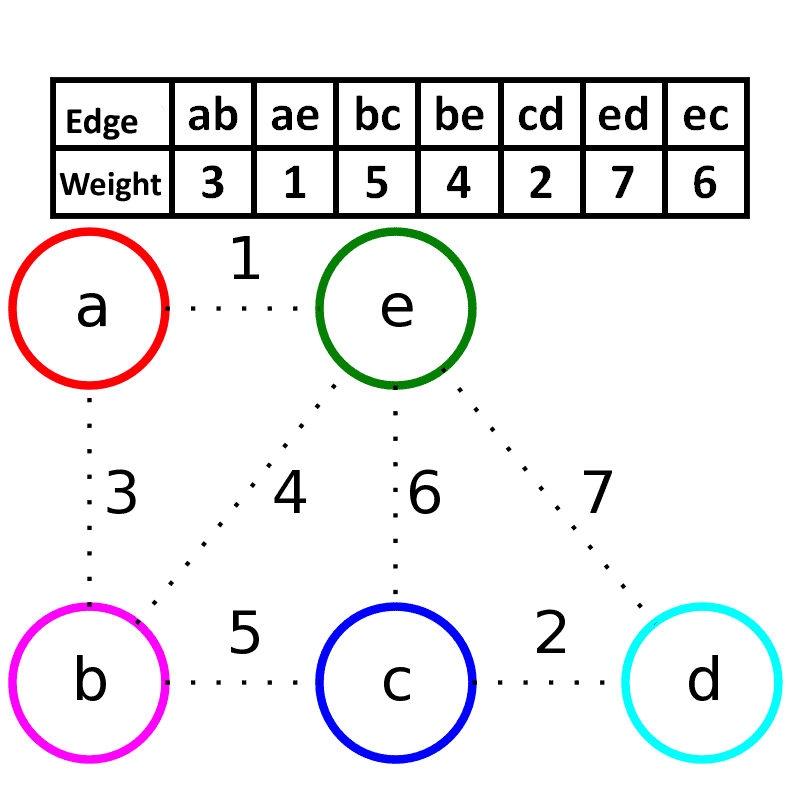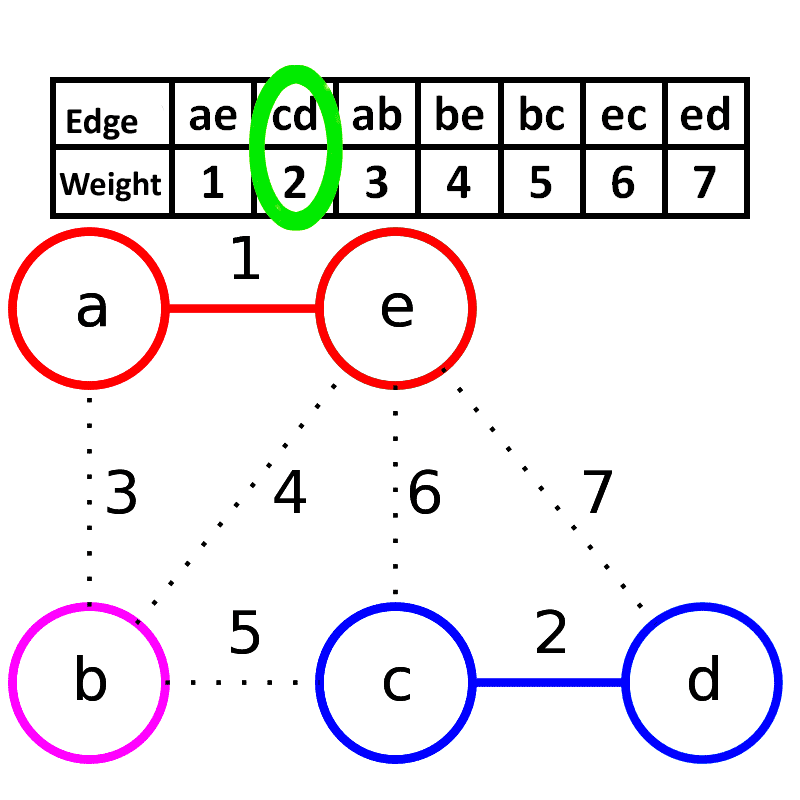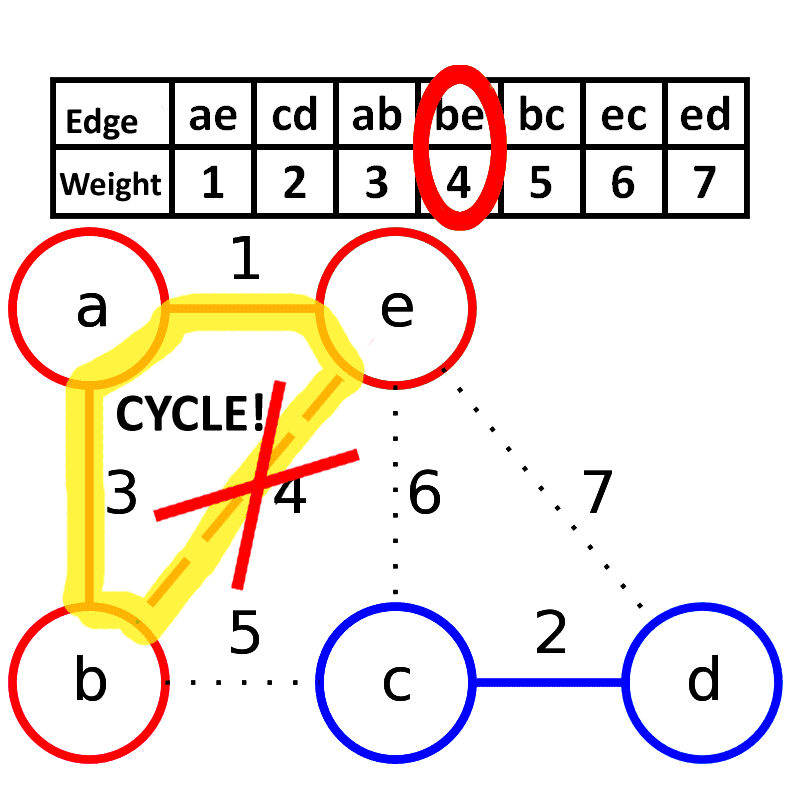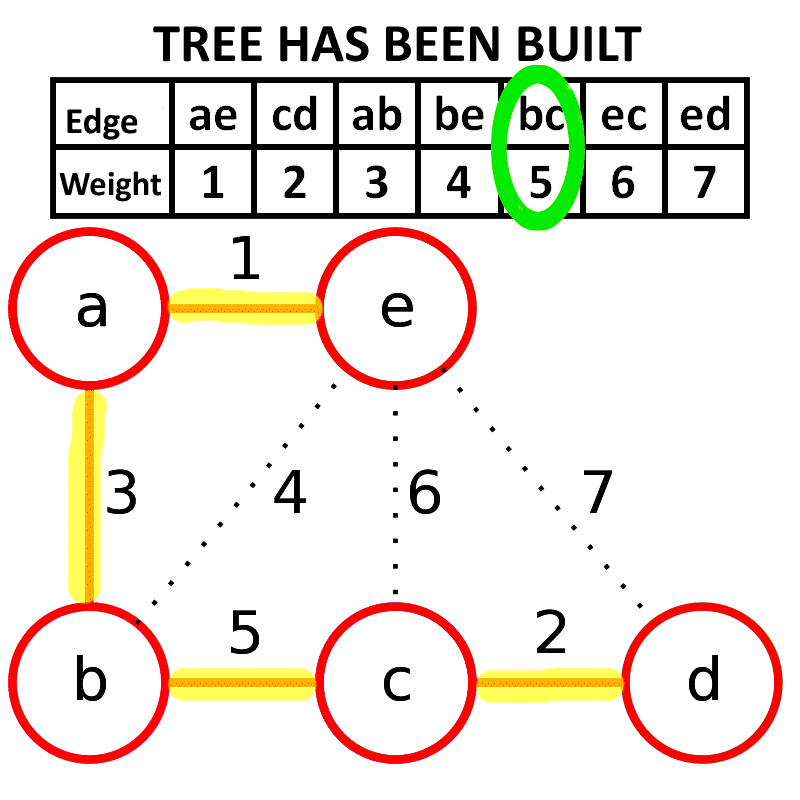
Minimal aufspannende Bäume
Aus ProgrammingWiki
Inhaltsverzeichnis |
Graphentheorie - minimaler Spannbaum
Ein Teilgebiet der Graphentheorie beschäftig sich mit der Frage, welche Weg muss man in gewichteten Graphen nehmen, um die best mögliche Strecke zwischen allen im Graphen vorhandene Knoten abzuschreiten. Best möglich richtet sich dann nach den entsprechenden Algorithmen bzw. gewichteten Kanten. Der sich daraus ergebene Graph nennt man minimalen Spannbaum, auch als Gerüst Spannwald oder aufspannder Wald bezeichnet. Ist nur in zusammenhängenden Graphen vorhanden, muss selber aber nicht zwingend zusammenhängend sein.
Begrifferläuterung
Die in der Einleitung verwendeten Begriffe werden in diese Kapitel ausführlich erläutert
Graphentheorie
- Die älteste bekannte Schrift zum Thema Graphentheorie schrieb Leonhard Euler (geb.1707)namens
- lat. solutio problematis ad geometriam situs pertinens
- dt: Lösung eines Problems zur Geometrie der Lage
- engl. The solution of a problem relating to the geometry of position
- solutio = Lösung
- probematis = Probleme
- ad = Präfix wie bei
- geometriam = Geometrie
- situs = Lage
- pertinens = sich beziehen auf
- Wird eingesetzt, wo graphentheoretische Probleme auftreten und Aussagen über Graphen bzw. deren Inhalt gemacht werden müssen.
- Wichtiges Teilgebiet der Mathematik, genauer der Kombinatorik.
Graph
- Ein rein mathematische Struktur, die fälschlicherweise mit der grafischen Abbildung gleichgesetzt wird.
- Kann zeichnerisch einer Menge an Punkten und ihre Zusammenhängen, den Geraden, darstellen.
- Graph is ein geordnetes Paar (V,E) G=(V,E)
- V = endliche Menge an Knoten(engl. vertices)
- E = Menge der Kanten(engl. edges) einer zweidimensionalen Teilmenge von V
Graphenkategorien
gewichtet/ungewichteter
- gewichteter Graph = knoten- und kantengewichteten Graphen werden den Knoten und/oder Kanten Werte zugeordnet
- ungewichteter Graph = den Kanten und/oder Knoten werden keine Werte zugeordnet
gerichtet/ungerichtet
- gerichtet Graph = Kanten sind Pfeile mit Richtung und nur in dieser kann der Graph durchlaufen werden
- ungerichtet = Kanten können in beide Richtungen durchlaufen werden
zusammenhängend/nicht zusammenhängend
- zusammenhängend Graph = in einem ungerichteten Graphen läßt sich jeder Knoten zwischen einem Start zu einem Endzustand erreichen
- nicht zusammenhängend Graph = besitzt mehr als eine Komponente und nicht jeder Knoten läßt sich zwischen einem Startzustand bzw. Endzustand erreichen
Baum
- Ein Baum ist ein Spezialform von Graph, der keine Kreise besitz.
- Unter anderen kann er dahingehend benutzt werden, eine Hierachien abzubilden, indem Elemente über- bzw untergeordnet werden
- Als Form des Graphen besitz er gleiche Eigenschaften. geordnetes Paar (V,E) G=(V,E)
- Bei Bäumen unterscheidet man wie bei Graphen zwischen gerichtet und ungerichte.
- Im Informatikbereich wird meist mit Bäumen gearbeitet, die eine Wurzel haben und gerichtet sind.
- Anders in der Graphentheorie, wo es Bäume wie den ungerichteten minimalen Spannbaum gib.
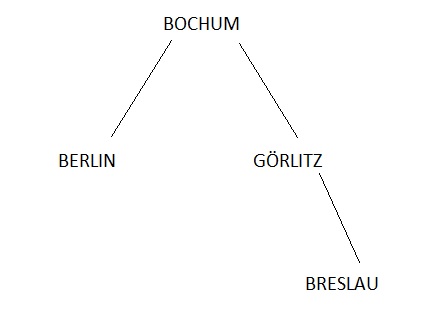
minimal Spannender Baum
- Alle Knoten eines ungerichteten Graphen verbindender minimal zusammenhängender Teilgraph.
- Dieser Spannwald hat auch Bezeichnungen wie auspannder Wald oder Spannwald.
- Ein in der Praxis recht häufige angewandte Problemlösungsstrategie. Überall wo der kürzeste
- Weg zwischen allen Punkten gesucht wird..
- Der vollständige Graph K_n enthält n^(n-2) unterschiedliche spannende Bäume.
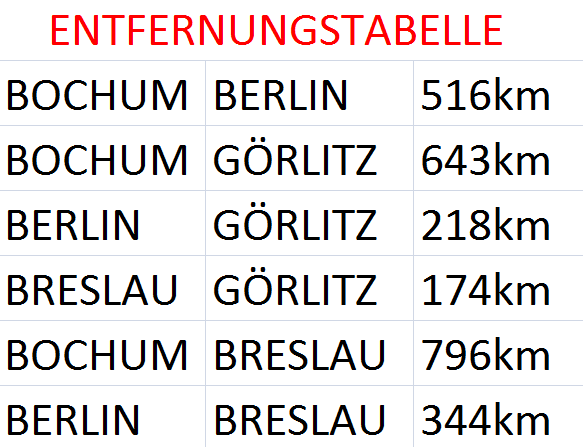
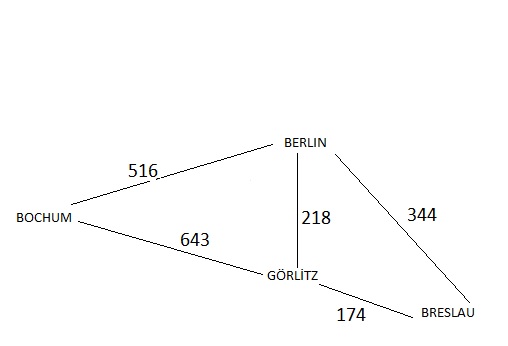
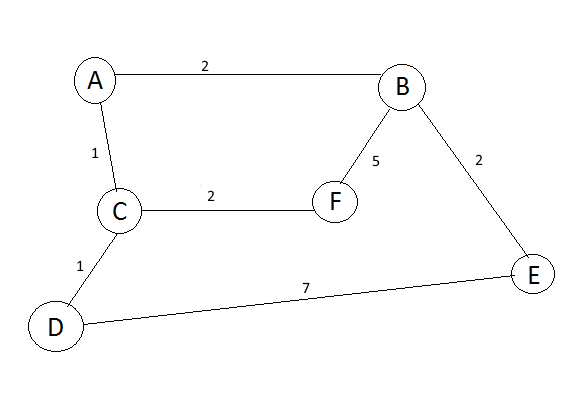
- Ein Beispiel ; Die schnellste weg von Bochum nach Breslau
Motivation
das Ziel besteht darin, eine Teilmenge E‘ ⊆ E auszuzeichnen, so dass a) der Teilgraph G‘ = (V,E‘) zusammenhängend ist und b) E‘ möglichst wenige Kanten hat
es sei G = (V,E) der folgende ungerichtete, zusammenhängende Graph, wobei jeder Kante eine reelle Zahl (ihr Gewicht) zugeordnet wird (/* z.B. ihre Länge ... */) .. das Ziel besteht darin, eine Teilmenge E‘ ⊆ E auszuzeichnen, so dass a) der Teilgraph G‘ = (V,E‘) zusammenhängend ist und b) die Summe der Gewichte der Kanten in E‘ möglichst klein ist
Anmerkungen;
- es sei G = (V,E) ein ungerichteter, zusammenhängender Graph mit
Gewichten an den Kanten
- es sei G‘ = (V,E‘) ein zusammenhängender Teilgraph von G mit einer
möglichst kleinen Summe der Gewichte der Kanten in E‘
- Dann gilt;
- 1) G‘ ist zyklenfrei.
- 2) G‘ enthält genau |V| - 1 viele Kanten.
- Warum ist diese Frage interessant?
die Knoten entsprechen Städte die Kanten geben an, welche Städte mit Stromleitungen verbunden werden können (/* aufgrund von geographischen Besonderheiten ist es nicht möglich, zwischen allen Städten Stromleitungen zu legen */) die Gewichte geben an, wie lang diese Stromleitungen sein müssten
>>>> es geht darum, ein möglichst kurzes Stromleitungsnetz zu finden, dass es erlaubt, alle Städte zu versorgen <<<<
- Andere typische Anwendungen ;
- -Verlegen von Telefonleitungen
- -Planung von hausinternen Versorgungsleitungen
Graphenthoeretiker
Leonhard Euler
- Leonhard Euler (* 15. April 1707 in Basel; † 7. Septemberjul./ 18. September 1783greg. in Sankt Petersburg)
- war ein Schweizer Mathematiker und Physiker. Wegen seiner Beiträge zur Analysis, zur Zahlentheorie und zu vielen weiteren Teilgebieten der Mathematik gilt er als einer der bedeutendsten Mathematiker.
- Erfinder der meisten Mathematische Symbolen
- Institutiones calculi differentialis (1755) und Institutiones calculi integralis (1768–1770) sind seine 2 Bekannteste Bücher im Gebiet Mathematik
Edsger W. Dijkstra
- Edsger Wybe Dijkstra(* 11. Mai 1930 in Rotterdam; † 6. August 2002 in Nuenen, Niederlande)
- war ein niederländischer Informatiker. Er war der Wegbereiter der strukturierten Programmierung. 1972 erhielt er den Turing Award für grundlegende Beiträge zur Entwicklung von Programmiersprachen.
William Thomas Tutte
- William Thomas Tutte (* 14. Mai 1917 in Newmarket; † 2. Mai 2002 in Kitchener-Waterloo)
- war ein britisch-kanadischer Kryptologe und Mathematiker. Während des Zweiten Weltkrieges half er entscheidend mit beim Entschlüsseln der kodierten Kommunikation der Wehrmacht. Seine Arbeit hatte wesentlichen Einfluss auf die Befreiung Europas durch die Alliierten. Weitere Leistungen sind seine grundlegenden Ergebnisse im Bereich der Kombinatorik und insbesondere der Graphentheorie.
Algorithmen
- In diesem Kapitel werden die Algorithmen vorgestellte, die bei der Suche nach dem minimalen Spannbaum Unterstützung bieten.
- Diese Algorithmen sind allesamt der Kategorie Greedy-Algorithmus
Greedy-Algorithmen
- Wie dem Namen zu entnehmen, handelt es sich um gierige/gefrässig Algorithmen, d.h. die Strategie die sich hinter diesem Algorithmus verbirgt, ist eine gefräßige.
- Versuch in einem Schritt so viel zu erreichen wie möglich und nimm der das beste Stücke, das du kriegen kannst.
- Welches Stück angemessen erscheint, wird mittels Algorithmus herrausgefunden.
- Ein Greedy-Algorithmus kommt ohne Rückgriff auf Werte, zum Beispiel Werte aus dem Cache und Entscheidungen werden nur einmal gefällt bzw. nicht zurückgezogen
Aufbau von Greedy-Algorithmen - Blickwinkel Graphentheorie
Bestandteile eines Greedy-Algorithmus
- (verbrauchende)Liste aller Knoten
- (aufbauende)Liste der Ergebnisse
- Funktion ergebnis? - ob sich eine Ergebnis für das Problem ergeben hat
- zulässig? - #t wenn Knoten zulässig ist
- next - wählt nächsten Knoten
- modi+ - Verändert Knotenliste, wenn es zu einer Erweiterung der Liste aller Knoten kommt
- modi- - Verändert Knotenliste, wenn es zu keiner Erweiterung der Liste aller Knoten kommt
- Resultat - Ausgabefunktion des Algorithmus
GENERIC-MST(G,w)
1 A = NULL
2 while $A$ A is not a spanning tree
3 $\;\;\;\ $do find an edge (u, v) $\left(u,v\right)$, that is safe for $A$ ist
4 $\;\;\;\ A = A ∪ {(u, v)}$
5 end while
5 return $A$
Greedy Prozedure in Dr Racket
Algorithmus von Prim
- 1. Schritt:
- Suche eine Kante mit minimalen Kosten.Diese Kante bildet mit den zugehörigen Endknoten den Anfang des Baums.
- 2. Schritt:
- Suche unter allen Kanten, die von einem Knoten des Baums zu einem Knoten führen, der nicht zum Baum gehört, eine mit minimaler Belegung und füge diese Kante mit ihren Endknoten dem Baum hinzu.
- Wiederhole diesen Schritt, bis es keinen solchen Knoten mehr gibt
- Behauptung:
- Der Algorithmus von Prim endet mit einem minimalen spannenden Baum.
Der Algorithmus wurde 1930 vom tschechischen Mathematiker Vojtěch Jarník entwickelt. 1957 wurde er zunächst von Robert C. Prim und dann 1959 von Edsger W. Dijkstra wiederentdeckt.
Ist auch als Prim-DijkstraAlghoritmus bekannt.
- Animation link [ http://new-lv.de/prim1.gif ]
GENERIC-MST(G,w)
1. Make a queue (Q) with all the vertices of G (V);
2. For each member of Q set the priority to INFINITY;
3. Only for the starting vertex (s) set the priority to 0;
4. The parent of (s) should be NULL;
5. While Q isn’t empty
6. Get the minimum from Q – let’s say (u); (priority queue);
7. For each adjacent vertex to (v) to (u)
8. If (v) is in Q and weight of (u, v) < priority of (v) then
9. The parent of (v) is set to be (u)
10. The priority of (v) is the weight of (u, v)
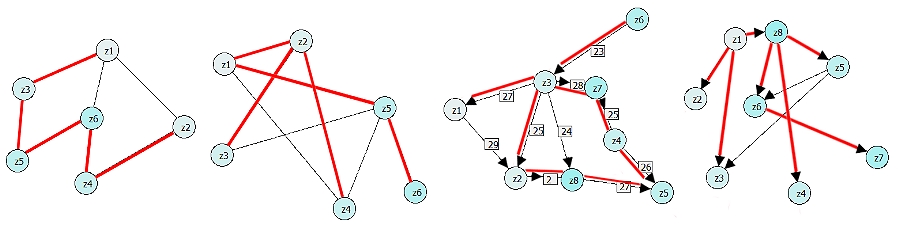
Algorithmus von Kruskal
- Mit einzelne Bewertung von Kantenwerte versucht man die Minimal Spannender Baum zu finden. Es kann mehrere Bäume ausgeben.Er ist nach Joseph Kruskal benannt, der diesen Algorithmus 1956 veröffentlichte.
Wir gehen die Kanten in der Reihenfolge ihres Gewichtes durch und fügen eine Kante zur Menge T hinzu, wenn sie nicht innerhalb einer bereits zusammenhängenden Menge verläuft.
- Schritt 1: Man wähle eine Kante e_1
von G, so dass ω(e_1) so klein wie möglich und e_1 keine Schlinge ist.
- Schritt 2: Wenn die Kanten e_1,e_2,...,e_i
gewählt wurden, suche man die Kante e_i+1, die noch nicht gewählt worden ist, so dass zum einen der entstehende Untergraph G[{e_1,...e_i+1}] azyklisch ist und zum anderen ω(e_i+1) so klein wie möglich ist, allerdings immer unter Berücksichtigung der ersten Bedingung.
KRUSKAL(G):
1. A = ∅;
2. for each v ∈ G.V:;
3. MAKE-SET(v);
4. for each (u, v) ordered by weight(u, v), increasing:
5. if FIND-SET(u) ≠ FIND-SET(v):
6. A = A ∪ {(u, v)}
7. UNION(u, v)
8. Return A
- Übung
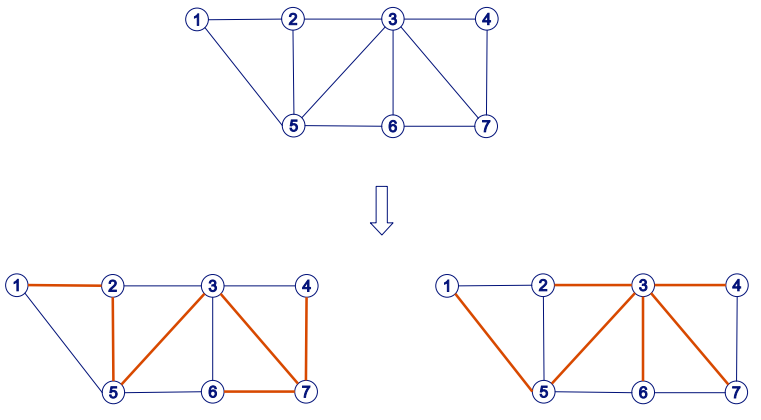
Unterschiede zwischen Prim und Kruskal
- Kruskal : Führt zu zahlreichen , gleichzeitig gebildeten Unterbaumen die dann zusammen gefügt werden
Kann dadurch bestimmt Zykln ermitteln zu können
- Prim : Führt zu einem einzigen,von einem Anfangsknoten ausgehenden,kontinuierlich anwachsenden Unterbaum.
Das Problem hier beinhaltet dass kein bereits gewaehlter Knoten nochmals ausgewahlt werden.
Implementierung
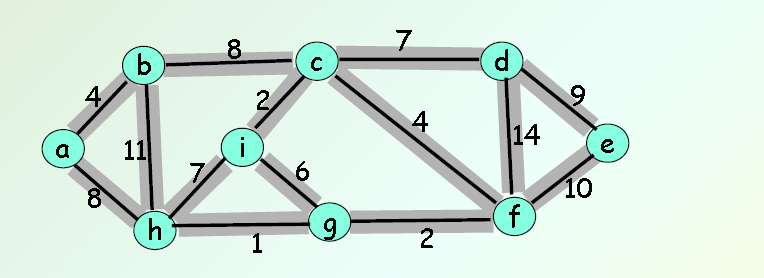
Anwendungsbeispiele
Tool algorithmus-2
- Kurze Einweisung in das Scheme Programm Algorithmus-2.
- Ermöglich das Erstellen von Graphen und Bäumen bzw. errechnet anhand des gewählten Algorithmus den minimalen Spannbaum.
[[[Link-Text http://new-lv.de/algorithmus-2.zip]]]
Wüstenstadt Dehram
Die Wasserversorgung einer ganzen Region soll dahingehende optimiert werden, das jedes Dorf in der näheren Umgebung Zugang zu fließend Wasser erhält. Dabei sollen die Gesamtkosten für 400€ pro Meter möglichst gering ausfallen. Die angegebene Strecken zwischen den Dörfern wird in Kilometer gewichtet.
Solar Holiday
Ein Flugunternehmen biete interstellar Reisen zu anderen Sonnen an. Mit weit über Lichtgeschwindigkeit werden 5 Lichtjahr an einem Tag zurückgelegt. Finden sie den kürzesten Weg zwischen allen Sonnen und berechnen sie die Reisedauer.
Quellen
- https://de.wikipedia.org/wiki/Spannbaum
- Christian Wagenknecht, Algorithmen und Komplexität, 2003
- http://www-e.uni-magdeburg.de/harbich/mst/mst.pdf
- https://books.google.de/books?id=aU6CBwAAQBAJ&pg=PA102&lpg=PA102&dq=minimaler+spannender+baum&source=bl&ots=bEcYNT5ftO&sig=7kW1drGRJMSUM0r6w_BIB1kvHzU&hl=tr&sa=X&ved=0ahUKEwjC0b6PksnJAhXBGw8KHbf1DOMQ6AEIQDAD#v=onepage&q=minimaler%20spannender%20baum&f=false