Matching-Probleme
Aus ProgrammingWiki
Leonard Mory, Felix Lüpke
Inhaltsverzeichnis |
Thematischer Einstieg und Motivation
Erläuterung
- bei Matching-Problemen handelt es sich um spezielle Zuordnungsprobleme
- werden auch als Zuteilungsprobleme bezeichnet
- Gegenstand ist die optimale Zuordnung der Elemente zweier disjunkter Mengen
- Zuordnungsprobleme sind z.B. Bewerber auf freie Stellen, Lehrer auf Schulklassen
- eine erfolgreiche Paarbildung nennt sich Matching
Definition
- Ein Graph $G=(V,E)$ heißt bipartiter Graph, wenn man die Knoten $V$ in zwei disjunkte Mengen $U$ und $W$ zerlegen kann, so dass alle Kanten zwischen $U$ und $W$ verlaufen.
Matching
- Ein Matching von $G=(V,E)$ ist eine Teilmenge $M ⊆ E$ der Kanten von $G$ mit der Eigenschaft, dass keine zwei Kanten einen gemeinsamen Knoten besitzen.
- ein Knoten kann nur zu einer Matchingkante gehören
- zwei Matchingkanten dürfen niemals adjazent sein
Maximales Matching
- Ein Matching $M$ von $G$ ist maximal, wenn jedes Hinzufügen einer weiteren Kante zu $M$ das Matching zerstört. Die Knoten der Kanten, die zu einem Matching gehören, nennt man vom Matching überdeckt.
- Wenn der Graph aus $n$ Knoten besteht, kann ein maximales Matching $\frac{n}{2}$ Kanten beinhalten
- Ein maximales Matching wird auch "nicht erweiterbar" genannt
$M$ ist maximal, wenn: $\nexists e \in E \setminus M \colon \{ e\}\cup M$ ist Matching
- Es ist wichtig den Unterschied zwischen einem erweiterten- und einem völlig anderen Matching zu erkennen
Perfektes Matching
- Sind alle Knoten von $G$ von einem Matching überdeckt, so handelt es sich um ein perfektes Matching.
- damit ist die maximale Mächtigkeit eines Matching erreicht
- Anzahl $n$ der Knoten muss dafür eine gerade Zahl sein
$M$ ist perfekt, wenn: $\forall v,w \in V$, mit $w \neq v\colon \space \exists e(v,w) \in M$
Zusammenhang
Finden Sie das größtmögliche maximale Matching
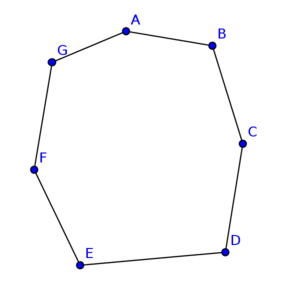
Jedes perfekte Matching ist maximal, aber nicht jedes maximale Matching ist perfekt.
Ausgangssituation
- Behandelt werden ausschließlich Probleme von zwei Mengen
- Somit fällt die Betrachtung auf bipartite Graphen
Beispiel
Tafelbild Seminargruppen -->
Man stelle sich vor, es stünden an einer Hochschule Seminargruppen zur Auswahl. In jeder Gruppe ist noch ein Platz frei. Demgegenüber steht eine Gruppe von Studierenden, deren Größe Ähnlich der der Seminargruppen ist. Zudem interessieren sich nicht alle Studierenden gleichermaßen für jedes Seminar.
Hat man es mit kleinen Gruppen zu tun, fällt eine Zuordnung auf dem Papier durch genaues Hinschauen noch leicht. Werden die Gruppen aber größer (z.B. bei Computerspielen -> Matchmaking), so wird Software benötigt.
Matchings für bipartite Graphen
- Ein Graph $G = (V,E)$ heißt bipartit, wenn sich die Knotenmenge $V$ in zwei disjunkte Teilmengen $V1$ und $V2$ zerlegen lässt, sodass keine Kante von $G$ zwei Knoten derselben Teilmenge miteinander verbindet. Ein bipartiter Graph mit maximal möglicher Kantenanzahl heißt vollständig bipartit und wird mit $K_{r,s}$ bezeichnet, wenn $r$ bzw. $s$ die Anzahlen von $V1$ bzw. $V2$ sind.
- Alle Kanten verbinden nur jeweils einen Knoten aus $V1$ mit einem Knoten aus $V2$
Hinweis: Das Stellen und Bearbeiten von Matchingproblemen setzt keinesfalls einen Bipartiten Graphen voraus, bietet sich jedoch an. Einem nicht bipartiten Graphen, für den ein Matching existiert, können wir dennoch einen bipartiten Kontext "unterstellen".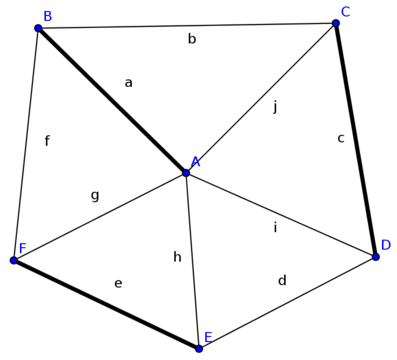
Heiratssatz von Hall
- Name kommt vom früher verbreiteten Problem, eine Gruppe Frauen zu verheiraten
- aber nur, wenn es eine gleichgroße Gruppe Männer gibt
- die sich mindestens für eine Frau der Gruppe interessieren
Grad einer Knotenmenge:
- Es sei $G = (V,E)$ ein Graph und $U$ eine Teilmenge der Knoten $V$ $\space \space (U \subseteq V)$. Wir definieren den Grad von $U$ als die Anzahl derjenigen Knoten von $G$, die mit einem Knoten aus $U$ eine Kante bilden, und schreiben dafür $d(U)$.
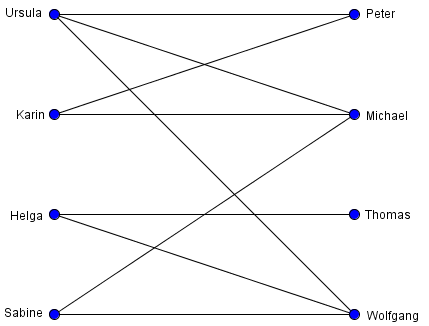
- für die Teilmenge $U=${$Ursula, Karin$} gilt $d(U)=3$, da drei Kanten zu einer anderen Teilmenge führen (Peter, Michael, Wolfgang)
Jetzt kann man den Satz von Hall verständlich formulieren:
- Ein bipartiter Graph $G = (V1 ∪ V2,E)$ besitzt genau dann ein perfektes Matching, wenn für alle Teilmengen $U1 ⊆ V1$ die Ungleichung $d(U1) ≥ |U1|$ erfüllt ist.
- zur Untersuchung wird der Graph in zwei Teilmengen zerlegt
- $V1=${$Ursula (1), Karin (2), Helga (3), Sabine (4)$} und $V2=${$Peter, Michael, Thomas, Wolfgang$}
- eine Kante bedeutet, dass beide Personen aneinander interessiert sind
- jetzt müssen alle 15 Teilmengen von $V1$ überprüft werden, wir begrenzen uns aber nur auf Teilmengen die den Knoten 1 enthalten
| d({1}) | = 3 ≥ 1 |
| d({1, 2}) | = 3 ≥ 2 |
| d({1, 3}) | = 4 ≥ 2 |
| d({1, 4}) | = 3 ≥ 2 |
| d({1, 2, 3}) | = 4 ≥ 3 |
| d({1, 2, 4}) | = 3 ≥ 3 |
| d({1, 3, 4}) | = 4 ≥ 3 |
| d({1, 2, 3, 4, }) | = 4 ≥ 4 |
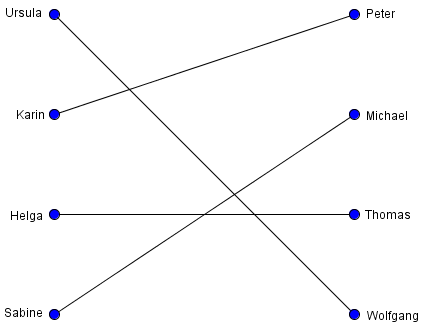
- wenn kein Widerspruch gefunden wird, besagt der Heiratssatz, dass ein perfektes Matching existiert
| Wahl | Ursula | Karin | Helga | Sabine |
|---|---|---|---|---|
| 1 | Peter | Peter | Thomas | Wolfgang |
| 2 | Michael | Michael | Wolfgang | Michael |
| 3 | Wolfgang | - | - | - |
| Wahl | Peter | Michael | Thomas | Wolfgang |
|---|---|---|---|---|
| 1 | Karin | Sabine | Helga | Ursula |
| 2 | Ursula | Karin | - | Helga |
| 3 | - | Ursula | - | Sabine |
- nur für kleine Interessengraphen
Maximal-Matching-Algorithmen
Greedy-Matching-Algorithmus
Es handelt sich um einen Algorithmus, in welchem, gemäß dem Konzept des Greedy-Verfahrens, am Ende eines Schritts stets der aktuell bestmögliche Folgeschritt gewählt wird. Der Vorteil liegt in der Schnelligkeit, mit der Ergebnisse produziert werden, welche allerdings nicht immer optimal sind.
- Es gibt eine Kandidatenliste, welche $E$ von $G$ entspricht und verbrauchend gelesen wird
- die sich aufbauende Resultatliste entspricht $M$
- wenn die Kandidatenliste leer ist, ist die Lösung gefunden (entspricht Funktion lösung?)
- die Funktion okay? erübrigt sich bzw. ergibt sich implizit aus der Frage nach allen Nachbarn eines Kandidaten
- naechster entspricht einem Iterationsschritt
- modify+ entspricht dem Hinzufügen zur Kandidatenliste
- modify- und ziel werden nicht benötigt
Ausgangssituation
Gegeben sei ein Ausgangsgraph $G = (V,E)$ und ein Matching $M$. Zum Schluss soll $M$ ein maximales Matching sein.
Pseudocode
1 Setze $M := \varnothing$ 2 Wähle eine Kante $e \in E$, füge $e$ $M$ hinzu 3 Entferne $e$ und alle benachbarten Kanten aus $E$ 4 Falls $E \neq \varnothing$ gehe zu 2, sonst STOPP: $M$ ist maximal
Das Ergebnis ist stets ein maximales Matching.
Verbessernde Wege (Verbessernde Pfade)
- Mit verbessernden Wegen kann ein gefundenes maximales Matching optimiert werden.
Gibt es für einen Graphen $G$ mit einem Matching $M$ einen Weg $P(v_0, v_1 , v_2, ..., v_n)\colon \{ v_0,v_n\} \cap M = \emptyset$,
mit ungerader Knotenanzahl, wobei jede zweite Kante $\subseteq M$, so nennt man $P$ einen
($M$-)verbessernden Weg
- Existiert ein verbessernder Weg, so kann dieser invertiert und die Zahl der Matchingkanten um eins erhöht werden.
- Ein verbessernder Weg $P$ wird invertiert, indem Matching-und Nicht-Matchingkanten ausgetauscht werden (swap).
- Ein invertierter Weg $P$ heißt $P^{-1}$.
Ausgangssituation
- Gegeben sei ein Graph $G$ mit einem maximalen Matching $M$. $M$ soll zu einem maximalen Matching mit maximal möglicher Kantenanzahl werden (Maximum-Matching).
Pseudocode
$M:=$maximales Matching
while $G$ enthält $M$-verbessernden Weg do
entferne $P$ aus $G$ und füge $P^{-1}$ hinzu
endwhile
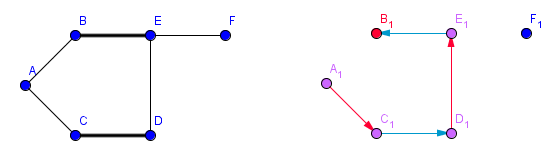
Symmetrische Differenz
- Gegeben seien zwei Graphen $G=(V,EG)$ und $H=(V,EH)$ mit gleicher Knotenmenge $V$.
- $GΔ H$ ist ein Graph mit der Knotenmenge $V$ und der Kantenlänge $E={e\mid e \in EG XOR e \in EH$.
- $M Δ M' = (M - M') \cup (M' - M)$
- $M$ und $M'$ sind zwei Matchings in $G=(V1 \cup V2,E)$
- jede Zusammenhangskomponente ist ein Kreis gerader Länge oder ein Pfad.
Satz von Berge
- wie bei dem Greedy-Algorithmus sieht man, dass der Algorithmus terminieren muss
- bei Zeile 3 wird M um eine Kante vergrößert
- das Bewies Claude Berge (1926-2002)
- M sei ein Matching von G
- M ist ein Maximum-Matching, wenn es keinen verbessernden Pfad gibt
- angenommen M ist kein Maximum-Matching, d.h. es existiert ein Matching $M'$ mit $|M'|>|M|$
- jeder Knoten von $G=[M Δ M']$ ist jeweils mit einer Kante aus $M$ und $M'$ verbunden
- jede Zusammenhangskomponente von $G=[M Δ M']$ ist sozusagen ein Kreis oder ein $M$ - alternierender Pfad
- $|M'|>|M|$ besagt, dass es eine Zusammenhangskomponente geben muss, die ein Pfad ist und eine Kante mehr aus $M'$ hat
- dieser Pfad ist verbessernd
- Berge bewies damit, dass der Algorithmus für beliebige Graphen Funktioniert
- Wie kann man auf systematische Weise $M$-verbessernde Pfade in Graphen finden?
Tiefensuche
- auch Depth-First-Search (DFS) genannt
- eine Standard-Suchmethode für Graphen neben der Breitensuche
- sind Algorithmen, die bei einem Knoten $v$ des Graphen beginnen und entlang der Kanten die von $v$ erreichbaren Knoten sucht
procedure explore(vertex v)
begin
/* Tu hier irgendwas mit v */
for all (v,u) in E do
if(u.visited=false) then
u.visited=true
explore(u)
endif
endfor
end
procedure DFS(Graph G)
begin
for all v in V do
if(v.visited=false) then
explore(v)
endif
endfor
end
- man braucht 2 Prozeduren:
- explore (vertex v) wird aufgerufen, wenn der Knoten $v$ das erste mal entdeckt wird
- daraufhin wird explore (u) rekursiv für alle unbesuchten Knoten aufgerufen
- besuchte Knoten (v) werden mit der boolschen Variable .visited markiert
- DFS(Graph G) ist die Oberprozedur, die den Graphen überblickt und für jede Zusammenhangskomponente explore(v) aufruft
- die Laufzeit von explore(v) hängt von der Anzahl der Kanten, die mit v zusammenhängen, ab ($O=(|V|+|E|)$)
M-alternierende Tiefensuche
- Tiefensuche soll M-verbessernde Pfade finden
- explore($v$) muss auf einen freien Knoten $v$ des Graphen aufgerufen werden
- immer zwei Schritte
- als erstes über eine ungematchte Kante ${v,u}$ zu einem Knoten $u$
- von $u$ aus über die eindeutige Matchingkante ${u,w}$ (falls vorhanden)
- dann rekursiv weiter
- wenn ein freies $u$ gefunden wird -> M-verbessernder Weg
- Suche wird abgebrochen
- auf dem Rückweg werden die überquerten Kanten umgedreht
- .match speichert den mit v gematchten Knoten
// Gibt true zurück, falls es von v aus einen M-verbessernden Pfad gibt & invertiert diesen dann.
bool invertPath(vertex v)
begin
for all (v,u) in E do
if(u.visited=false)
u.visited=true
if(u.match=NULL or invertPath(u.match)) //ist u frei oder führt zu eine
u.match=v //freien Knoten? Dann Kante invertieren
return true //und Suche abbrechen.
endif //Sonst nächste Kante anschauen
endif
endfor
return false //Alle Kanten erfolglos ausprobiert
end
- die Oberprozedur des Algorithmus ruft invertPath solange auf, bis es keine M-verbessernden Pfade mehr gibt
MaxBipMatching(BipartiteGraph g)
begin
vertex_list L := g.getPartition()
for all v in L do
unmark(g) //Entfernt alle Knotenmarkierungen
invertPath(v)
endfor
end
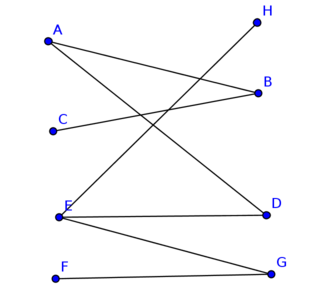
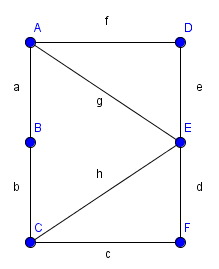
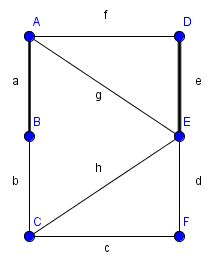
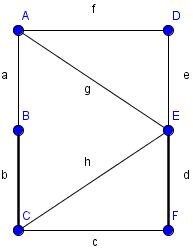
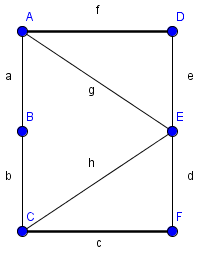
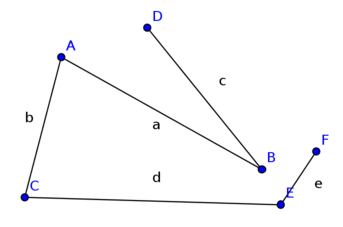
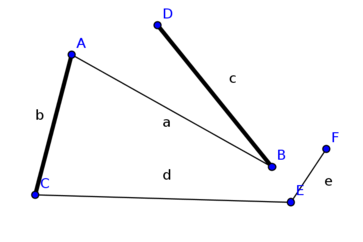
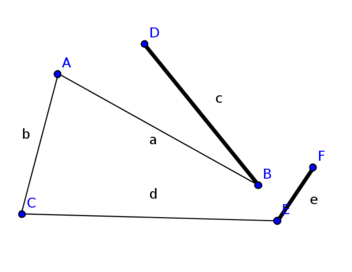
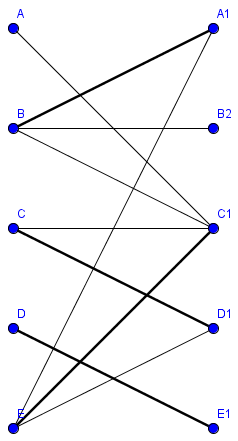
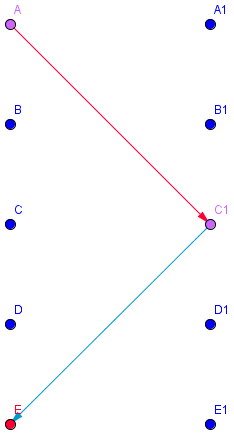
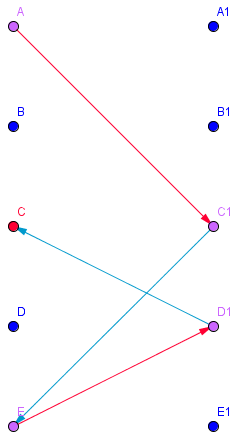
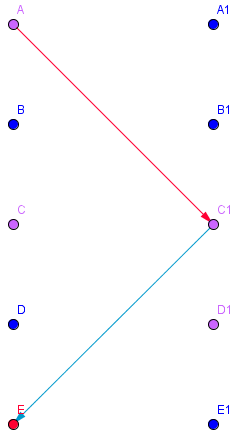
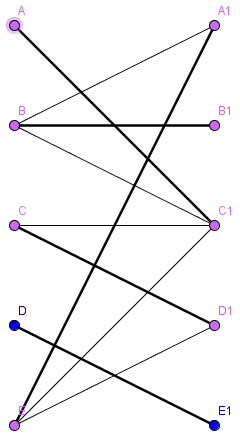
Einschränkung auf bipartite Graphen
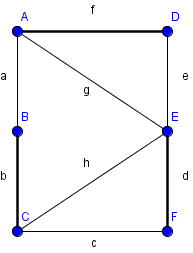
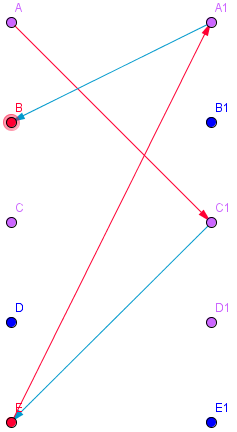
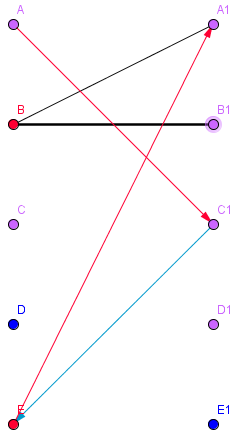
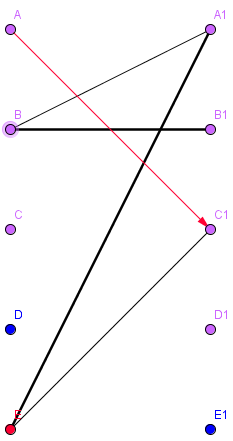
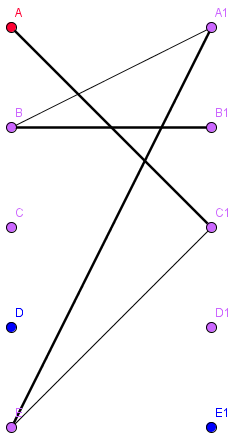
- Algorithmus (Tiefen- Breitensuche) funtioniert für nicht-bipartite Graphen nicht
- Algorithmus läuft in eine Sackgasse
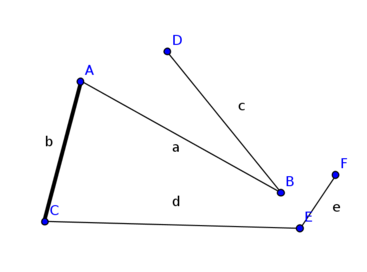
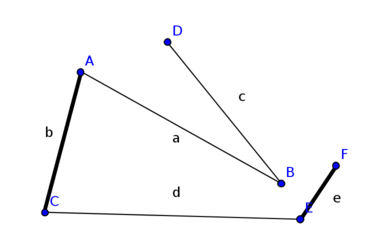
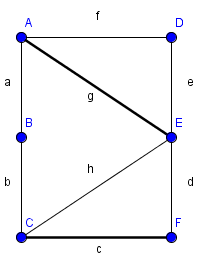
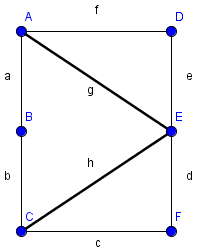
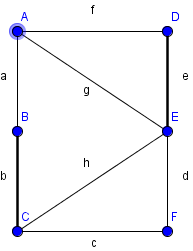
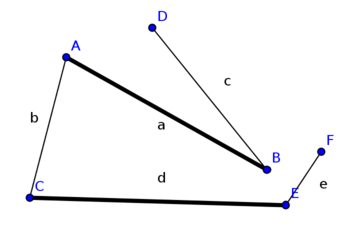
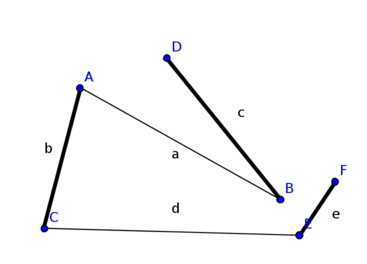
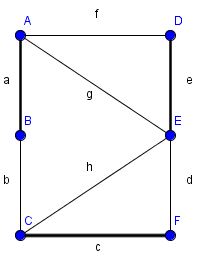
- findet den M-verbessernden Weg ABEF nicht
Quellen
- https://books.google.de/books?id=2qkkBAAAQBAJ&pg=PA45&dq=matching+probleme&hl=de&sa=X&ved=0CCIQ6AEwAWoVChMI_K-g08SFyQIVob5yCh19wwwa#v=onepage&q=matching%20probleme&f=false
- https://books.google.de/books?id=Rj0lBAAAQBAJ&pg=PA292&dq=matching+probleme&hl=de&sa=X&ved=0CD0Q6AEwBWoVChMI_K-g08SFyQIVob5yCh19wwwa#v=onepage&q=matching%20probleme&f=false
- http://matheplanet.com/default3.html?call=article.php?sid=1070&ref=https%3A%2F%2Fwww.google.de%2F
- http://algo.rwth-aachen.de/Lehre/SS11/VEA/Skripte/matchings.pdf
- https://www.tu-ilmenau.de/fileadmin/public/iti/Lehre/EAII/WS11/Kapitel2-Matchings.pdf
- http://parco.iti.kit.edu/henningm/KO/ko-folien-01b.pdf
- Christian Wagenknecht, Algorithmen und Komplexität, 2003