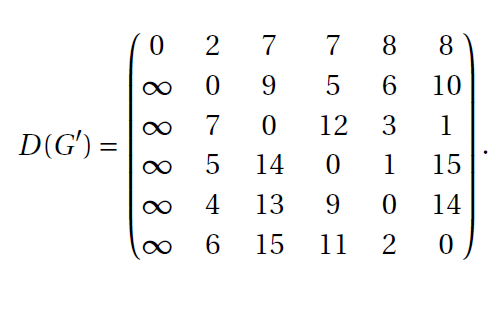Grundbegriffe der Graphentheorie 2
Aus ProgrammingWiki
Maik Geier, Anna Bremensztul
Inhaltsverzeichnis |
Einführung und Wiederholung
- Die Graphentheorie ist ein Teilgebiet der Mathematik, welche die Eigenschaften von Graphen und ihre Beziehungen zueinander untersucht.
- Ein Graph besteht aus einer Menge von Punkten (Knoten,Ecken) zwischen denen Linien(Kanten, Bögen) verlaufen.
- Der Grad eines Knotens ist die Summe der Kanten, welche an dem jeweiligen Knoten anliegen.
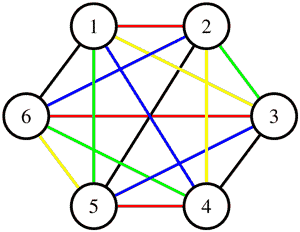
- Isomorphie --> Gleichstrukturiertheit von Graphen G∼G′
| G1 | G2 | G3 | G4 | ||
|---|---|---|---|---|---|
| G1 | |||||
| G2 | |||||
| G3 | |||||
| G4 |
- In der Graphentheorie bezeichnet Weg, Pfad, Kantenzug oder Kantenfolge eine Folge von Knoten, in welcher jeweils zwei aufeinander folgende Knoten durch eine Kante verbunden sind.
Wo können wir die verschiedenen Graphen nutzen?
„In der Mathematik ist die
Kunst des Fragenstellens öfter gebräuchlich als die
des Lösens!“
- Verkehrswege zwischen Städten – kürzeste Wege
- Transportwege mit Kapazitäten – maximale Flüsse
- Zugmöglichkeiten in Spielen – Gewinnstrategien
- Beispiele dafür sind auch die Netzwerke(Verkehr, Daten), Datenstrukturen oder Rechnerarchitektur.
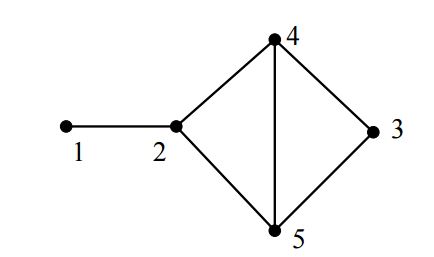
Wir können verschiedene Darstellungen von Graphen benutzen:
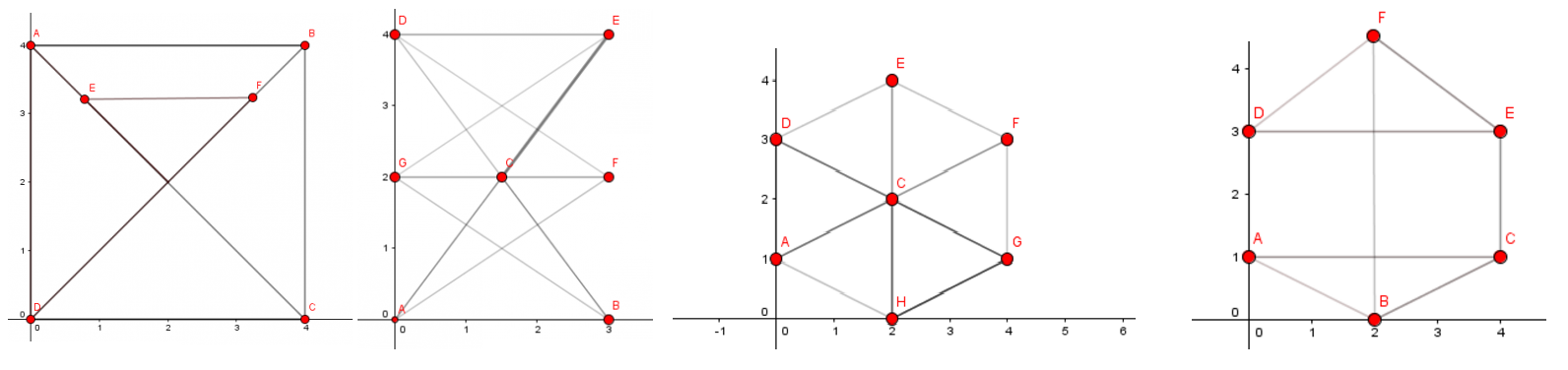
1. Darstellung als Zeichnung:
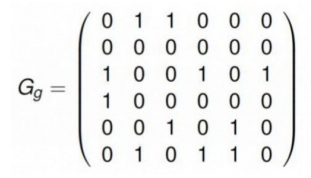
2. Darstellung als Adjazenzmatrix
Jedem Knoten wird eine Zeile und eine Spalte
zugeordnet und der Eintrag in der Zeile von u und der Spalte von v wird 1 gesetzt,
wenn {u, v} eine Kante des Graphen ist (sonst 0):
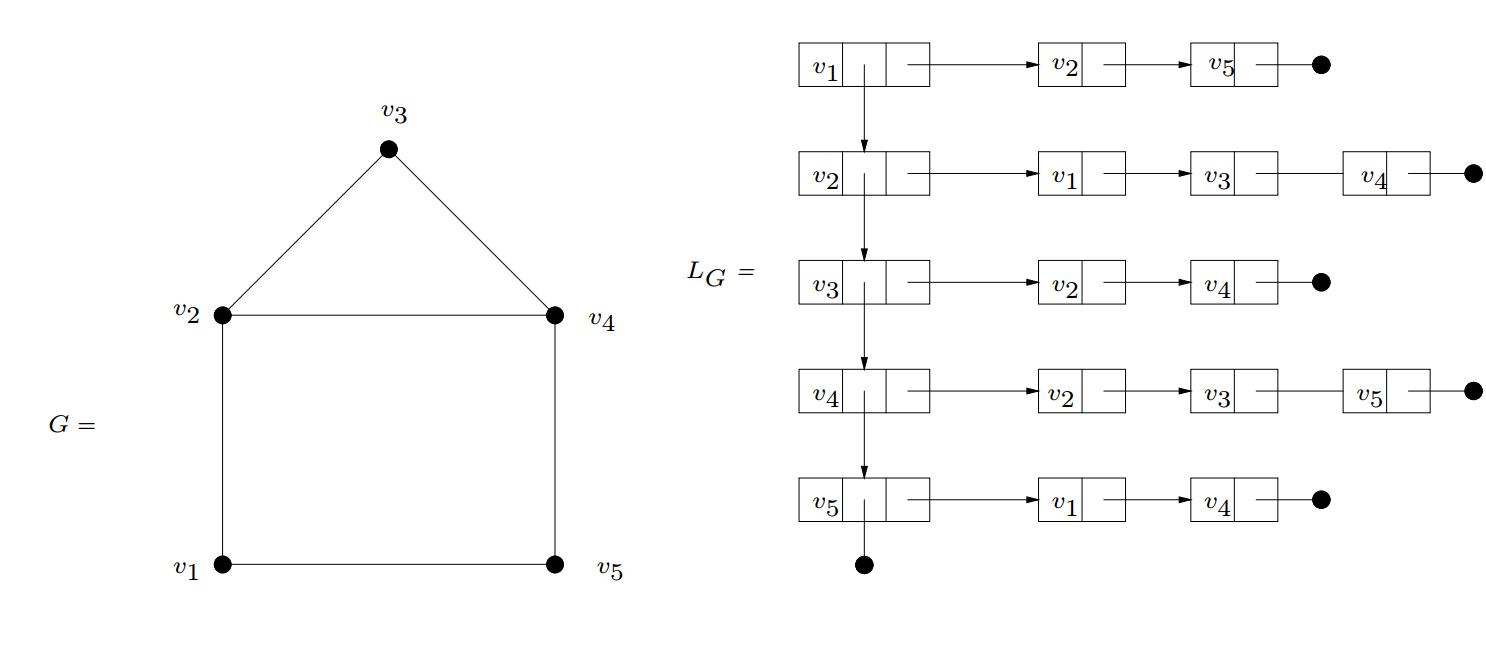
3. Darstellung als Adjazenzliste.
Für jeden Knoten wird die Liste seiner Nachbarn
angegeben (Liste von Listen).
Für die Behandlung algorithmischer Probleme sind oft Adjazenzlisten die Datenstruktur
der Wahl, weil sie die wahre Größe eines Graphen (Anzahl der Kanten) widerspiegeln.
Die Klassenkameraden haben im vorigen Woche eine Vollständige Graphen vorgestellt und Grundbegriffe der Graphentheorie erklärt.
Ein Graph heißt vollständig , wenn jede Ecke mit jeder anderen durch genau eine Kante verbunden ist.
Das heißt, bei einem vollständigen Graphen sind je zwei Ecken verbunden, aber nur durch eine Kante. Der vollständige Graph mit n Ecken wird mit K_n bezeichnet.
Dagegen möchten wir heute andere Typen von Graphen vorstellen.
1. Bipartite Graphen.
2. Gerichtete Graphen und Multigraphen
3. Bewertete Graphen
4. Bäume und Wälder
5. Gozinto-Graphen
Bipartite Graphen
Definition
Definition: Ein Graph G = (V,E) (V = Menge der Knoten, E = Menge der Kanten) heißt bipartit, wenn man seine Knoten so in zwei Teilmengen S und T aufteilen kann, dass folgende Regeln gelten:
- Die Mengen der Knoten besitzen keine gemeinsamen Elemente (disjunkt) und ergeben zusammen alle Knoten
- Kanten verlaufen immer nur von einer Teilmenge zur Anderen. Zwischen den Knoten, innerhalb der Teilmengen, verlaufen keine Kanten
Vollständig Bipartit
Der Graph G heißt vollständig bipartit, wenn jeder Knoten aus S mit jedem Knoten aus T verbunden ist und somit die Anzahl der Kanten maximal ist.
Der vollständige bipartite Graph G hat genau S + T Ecken und S · T Kanten
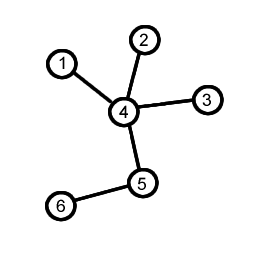
Ein vollständig bipartiter Graph, bei dem S=1 oder T=1 ist, heißt Sterngraph .
n-partiter Graph
Ein Graph heißt n-partit wenn er den Regeln der Bipartiten Graphen gehorcht, dessen Knotenmenge jedoch beliebig viele Teilmengen besitzt. Einen n-partiten Graph mit maximal möglicher Kantenzahl nennt man vollständig n-partit.
Eigenschaften
- Ein Graph ist genau dann bipartit, wenn es keinen aus einer ungeraden Anzahl von Kanten bestehenden geschlossenen Weg gibt. Kanten zwischen den Elementen einer Teilmenge sind dabei natürlich nicht erlaubt.
- Bei einem zusammenhängenden bipartiten Graphen ist die Zerlegung der Menge V = S + T eindeutig bestimmt.
- Ist G=(V,E) bipartit mit V = S + T , so gilt:
- Bei einem aus einer geraden Anzahl von Kanten bestehenden Weg gehören Start- und Endpunkt zur selben Menge S oder T.
- Bei einem aus einer ungeraden Anzahl von Kanten bestehenden Weg gehören Start- und Endpunkt zu verschiedenen Mengen.
- In einem bipartiten Graphen sind keine Kreise ungerader Länge möglich.
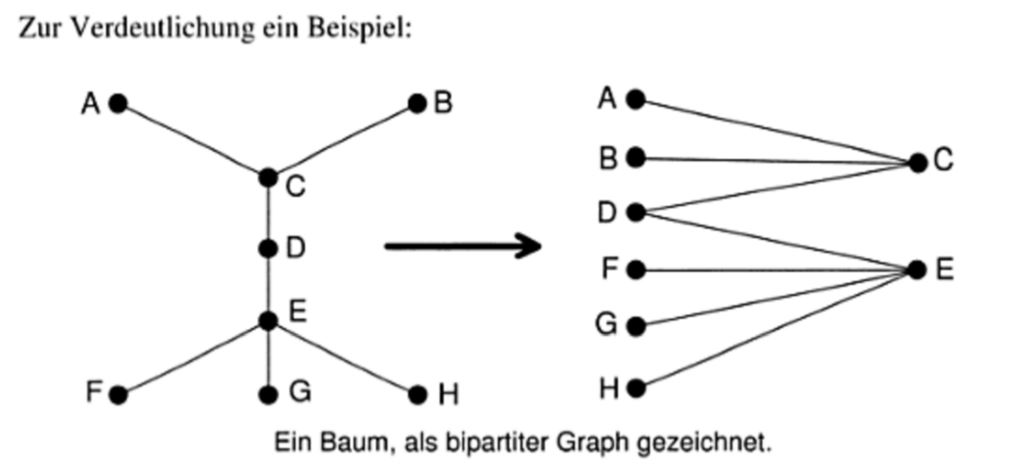
Ein Baum,als bipartiter Graph gezeichnet.
Konstruktion einer Zerlegung von V in S und T
Sei G = (V,E) ein zusammenhängender Graph, welcher eine disjunkte Zerlegung der Knotenmenge V in die Teilmengen S und T erhalten soll. Gelingt dies, so ist der Graph bipartit.
Ein möglicher Algorithmus zur Zerlegung sieht wie folgt aus:
- Markiere einen (beliebigen) Startknoten mit s.
- Markiere alle unmarkierten Knoten, die einen mit s markierten Nachbarknoten haben mit t.
- Markiere alle unmarkierten Knoten, die einen mit t markierten Nachbarknoten haben mit a.
- Wiederhole Schritt 2 und 3 so lange, bis entweder
- alle Knoten markiert sind oder
- zwei benachbarte Knoten die gleiche Markierung haben. In diesem Fall ist der Graph nicht bipartit und der Algorithmus kann abgebrochen werden.
Im günstigstem Fall erreicht man bei der Umsetzung dieses Algorithmus einen linearen Aufwand von $\mathcal{O}(V+E)$
Beispiel zu Bipartität
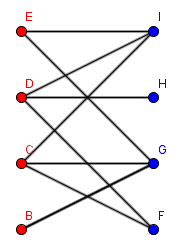
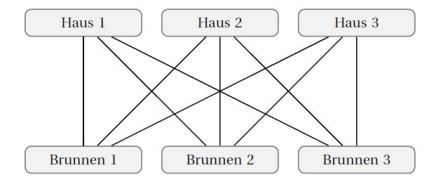
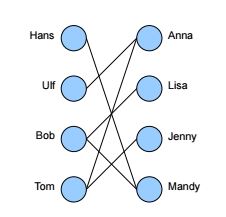
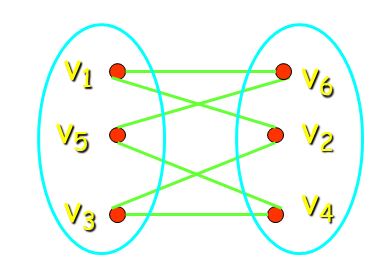
In einem Dorf gibt es drei Häuser und drei Brunnen. Jedes der Häuser soll nun mit jedem der
Brunnen durch einen Weg verbunden werden. Modelliert man dieses Problem mithilfe eines Graphen.
- Dieser Graph kommt auch als sogenannter GEW-Graph vor. Dieser Name basiert auf einer äquivalenten Realisierung des Problems mit drei Häusern und Werken für Gas, Elektrizität und Wasser.
- Die Menge der 6 Knoten lässt sich in 2 Teilmengen einteilen: die Häuser und die Brunnen. Dazwischen werden Kanten gezeichnet, aber innerhalb der Teilmengen finden sich keine Kanten: Kein Haus soll etwa mit einem anderen verbundenwerden.
Anwendung
Biparität eignet sich sehr gut zur Modellierung und zur Untersuchung von Zuordnungs- sowie Optimierungsproblemen. Des Weiteren lassen sich besonders für bipartite Graphen, aufgrund der bekannten Eigenschaften, viele Grapheneigenschaften mit deutlich weniger Aufwand berechnen als dies im allgemeinen Fall möglich ist.
- In der Informatik finden Bipartite Graphen besonders zur Modellierung Anwendung.
z.B. in den Endlichen Automaten, in welchen eine Biparität zwischen den Terminalen/Nichtterinalen und den Zuständen herrscht.
- Auch n-partite Graphen finden in der Modellierung anwendung.
z.B. können in Neuronalen Netzen mehrere Schichten gebildet werden, welche eingehende Reize intern bekannten Mustern zuordnen und daraus wiederum eine reaktion generieren. Diese Schichten bilden somit Teilmengen der Gesamtmenge Neuronen(Knoten).
Matchings
Definition: Sei der Graph G = (V,E) bipartit mit V = S + T. Eine Teilmenge M, der Kantenmenge E, nennt man ein Matching(oder Paarung), wenn jeder Knoten zu maximal einer Kante aus M inzident ist.
Ein Matching heißt maximal, wenn es kein anderes Matching gibt, welches mehr Kanten enthält.
Eine vollständige Paarung ist ein maximales Matching M und defniert eine bijektive Abbildung (1:1-Zuordnung) von S auf T, sodass jeder Knoten mit einer Kante aus M inzident ist. Nur möglich wenn |S|==|T|.
Anwendungsbeispiel
Männer und Frauen nehmen an einem Tanzkurs teil. Es sollen möglichst viele Paarungen gebildet
werden, jedoch keine bei denen sich Mann und Frau nicht mögen. Wieviele Paarungen kann
man maximal bilden?
| Beziehungsgraph | Antwort | ||
|---|---|---|---|
In dem gezeigten Beispiel war die richtige Antwort durch bloßes hinsehen ersichtlich.
Hat man jedoch Graphen mit hunderten von Knoten, so benötigt man entweder sehr viel Zeit oder einen Computer, welcher die Aufgabe mit einem Algorithmus löst.
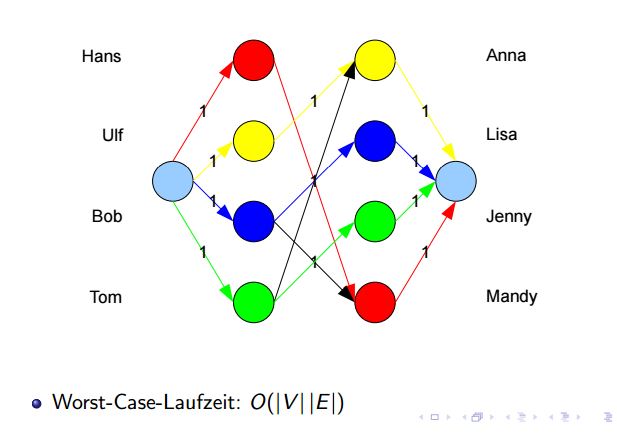
So kann man die maximale Paarung beispielsweise bestimmen, indem man den maximalen Fluss berechnen lässt.
¨ Dazu muss der Graph folgendermaßen transformiert werden:
- Füge eine Quelle hinzu und verbinde alle Knoten der ersten Teilmengeenge durch eine gerichtete Kante mit der Quelle
- Fuge eine Senke hinzu und verbinde alle Knoten der zweiten Teilmengeenge durch eine gerichtete Kante mit der Senke
- Ersetze die ungerichteten Kanten zwischen den beiden Mengen durch gerichtete Kanten
- Weise jeder Kante das Gewicht 1 zu
Berechnet man auf diesem Graphen den maximalen Fluss, also den Maximalbetrag welcher in der Senke ankommen kann, erhält man das maximale bipartite Matching. Dies funktioniert da alle Kanten den selben Wert besitzen und somit der maximale Fluss der maximalen Anzahl von Kanten entspricht.
Übung
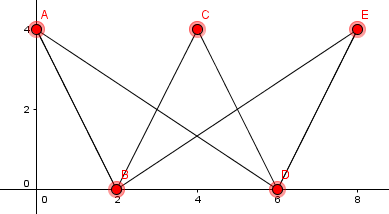
1. Ist diese Graph bipartite?
2. Fünf Jugendliche treffen sich zu einem gemeinsamen Frühstück. Jeder bringt etwas mit. Dazu wird eine Liste angelegt:
Steffi Brötchen , Tee
Niko Butter, Marmelade
Robert Marmelade, Saft
Anja Milch,Tee
Lars Käse ,Brötchen
? Kaffe
Man kann statt der Liste auch einen Graphen zeichen:
Ist diese Graph bipartit?
Der Vorteil des Graphen ist, dass man ihn in zwei Richtungen lesen kann: Man sieht nicht nur, was die einzelnen Personen mitbringen, sondern man sieht auch auf einem Blick, wer eine bestimmte Speise mitbringt.
Der Graph enthält zwei Sorten von Ecken: Leute und Lebensmittel. Und Kanten gibt es nur zwischen Leuten und Lebensmittel.
Gerichtete Graphen und Multigraphen
Einige Praxisanwendungen erfordern eine Erweiterung des bisherigen Graphenbegriffs, und zwar in zweierlei Hinsicht, nämlich den Kanten eine Richtung zu geben und Mehrfachkanten zuzulassen.
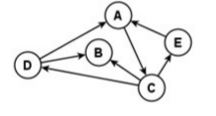
Gerichteter Graph
Definition:
Ein Graph G = (V,E) heißt gerichtet (auch: Digraph, von engl.: directed graph), falls seine
Kanten zusätzlich eine Orientierung erhalten. Diese orientierten Kanten nennen wir dann
auch Pfeile.
Die Richtung einer Kante in einem gerichteten Graphen wird in der Notation durch die Reihenfolge der Knotenangaben ersichtlich.
Eine Kante e(u, v) verläuft gerichtet von u nach v.
Das Einführen der Graphenrichtung hat nun zur Konsequenz, dass, wenn ein Weg in beide Richtungen möglich sein soll, eine einzelne Kante nichtmehr ausreicht.
Multigraph
Definition:
Ein (gerichteter oder ungerichteter) Graph G = (V,E) heißt Multigraph, falls er mehrfache
Kanten (d. h. verschiedene Kanten mit den gleichen Knoten) erlaubt, sowie auch solche
Kanten, die einen Knoten mit sich selber verbinden (sogenannte Schleifen oder Schlingen).
Zwei Kanten a, b mit a = (u, v) und b = (u, v) heißen parallel;
zwei Kanten a, b mit a = (u, v) und b = (v, u) heißen invers.
Bewertete Graphen
Definition: Eine Knotenmarkierung eines Graphen G =(V, E) ist eine Abbildung b:V->M die jedem Knoten v einen Wert oder ein Symbol zuordnet.
Definition: Eine Kantenmarkierung eines Graphen G =(V, E) ist eine Abbildung b:E->M die jeder Kante e einen Wert oder ein Symbol zuordnet. Für die Bewertung der Kante {u, v} schreiben wir dann kurz b(u, v).
Anwendungen
Gerichtete Graphen ergeben sich in natürlicher Weise aus vielen Anwendungsproblemen:
- Routenplanung
- Bei Straßennetzwerken enstehen gerichtete Graphen, sobald es Einbahnstraßen gibt.
- Verwendet man Gewichte, um die erwarteten Fahrzeiten/Strecke entlang einer Straße zu kodieren, gibt es Asymmetrien z.B. dann, wenn Straßen in einer Richtung bergab, in der anderen bergauf befahren werden. Hier existieren zwar Kanten in beiden Richtungen, sie haben aber unterschiedliche Gewichte.
- zeitliche oder kausale Abhängigkeiten
- Wenn die Knoten Ereignisse repräsentieren, von denen einige die Ursache von anderen sind, diese wiederum die Ursache der nächsten usw., verbindet man die Knoten zweckmäßig durch gerichtete Kanten, die die Kausalitätsbeziehungen kodieren. Handelt es sich um logische "wenn-dann"-Regeln, erhält man einen Implikationengraph. Handelt es sich hingegen um Wahrscheinlichkeitsaussagen, erhält man ein Bayessches Netz.
- Wenn bestimmte Aufgaben erst begonnen werden können, nachdem andere Aufgaben erledigt sind, erhält man einen Abhängigkeitsgraphen.
- Sequence Alignment
- Eine gute Rechtschreibprüfung markiert nicht nur fehlerhafte Wörter, sondern macht auch plausible Vorschläge, was eigentlich gemeint gewesen sein könnte. Dazu muss sie das gegebene Wort mit den Wörtern eines Wörterbuchs vergleichen und die Ähnlichkeit bewerten. Ein analoges Problem ergibt sich, wenn man DNA Fragmente mit der Information in einer Genomdatenbank abgleichen will.
Beispiele
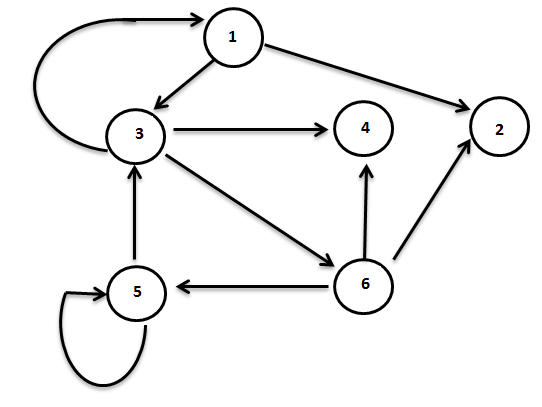
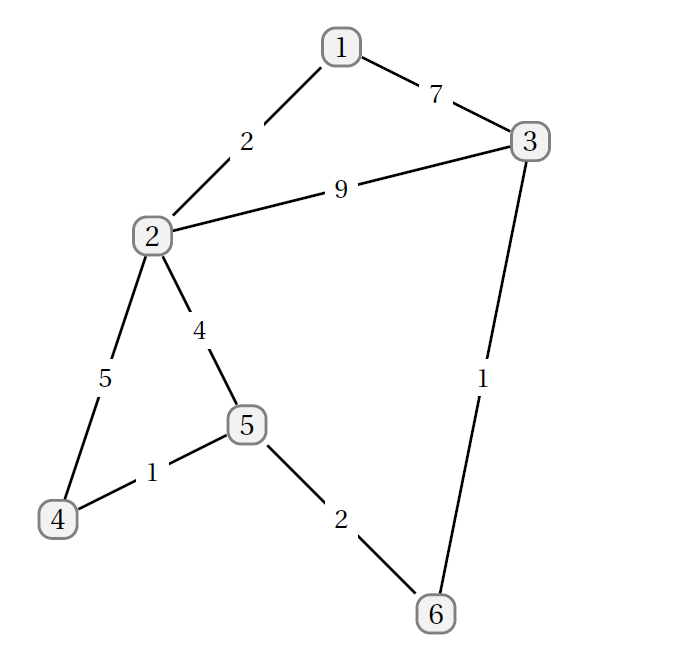
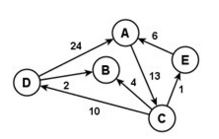
Wir betrachten den ungerichteten Graphen G im folgenden Bild. Man kann die Bewertungen
seiner Kanten beispielsweise als Entfernungen zwischen durch die Knoten gegebenen
Orten auffassen – oder als Kosten, um ein gewisses Gut entlang der entsprechenden
Kante zu transportieren.
Für den Weg(123) auf G gilt dann:
l(123)= 2+9 = 11.
Für den Weg(54236) auf G ergibt sich entsprechend
l(54236)= b(5,4)+b(4,2)+b(2,3)+b(3,6)= 1+5+9+1= 16.
| Graph-G | Entfernungs-Matrix | ||
|---|---|---|---|
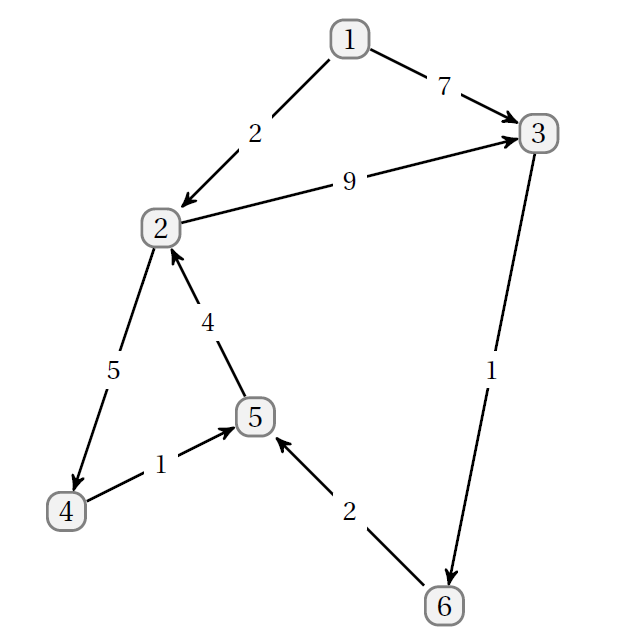
Schwierigkeiten können sich beispielsweise ergeben,
wenn die Kanten zusätzlich gerichtet sind: Betrachten wir etwa den gerichteten Graphen G', so könnte man hier analog zum
ungerichteten Graphen die Länge:
l(123)= 2+9= 11
berechnen, da dieserWeg über die Pfeile tatsächlich durchlaufen werden kann. Hingegen gibt
es den Weg(54236) in dem Graphen G' nicht.
| Graph-G' | Entfernungs-Matrix | ||
|---|---|---|---|
Gozinto-Graphen
Der Gozintograph ein Graph, der in der Fertigungsplanung zur Produkt- und Teilbedarfsrechnung sowie als Vorstufe zur Fertigungstermin- und Maschinenbelegungsplanung dient.
Vazsonyi prägte den Begriff scherzhaft, indem er die Vorgehensweise auf den (nicht existierenden) italienischen Mathematiker Gozinto zurückführte,
dessen Name für „the part that goes into” steht.
Für jedes Erzeugnis der industriellen Produktion lässt sich angeben,
aus welchen Baugruppen und Einzelteilen es besteht und wie viele Mengeneinheiten davon benötigt werden,
um eine Einheit des Erzeugnisses zu produzieren.
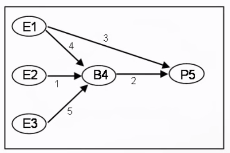
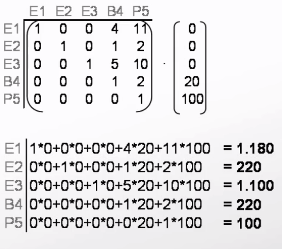
Angenommen wir haben einen Endprodukt P5, welches selber aus den beiden Baugruppen B4 und E1. Baugruppe B4 besteht aus den Teilen T1 und T2. Wir haben nun eine Bestellung über 100 P5 und 20 B4 erhalten und rechnen uns nun mit Hilfe des Gozinto-Graphens den Bedarf an Teilen aus. Die Struktur der Produktion sieht im Gozinto-Graphen dann so aus:
| Gozinto-Graph | Produktionsebenen/Primärbedarf | ||
|---|---|---|---|
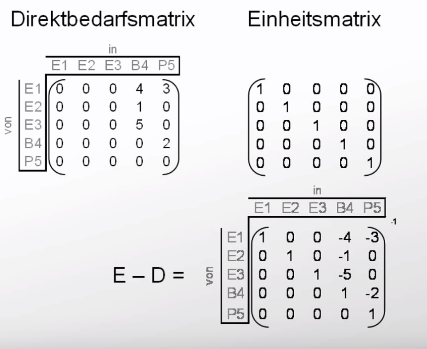
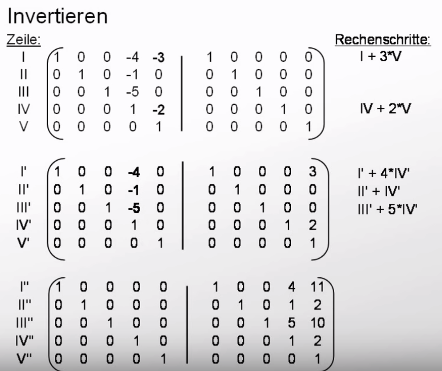
Herangehensweise: --> 1.Direktbedarfsmatrix (Knoten x Knoten) aufstellen --> 2.Direktbedarfsmatrix von Einheitsmatrix subtrahieren --> 3.Matrix Invertieren --> 4.Inverse mit Primärbedarfsvektor multiplizieren </p>
| Schritt 1 & 2 | Schritt 3 | Schritt 4 | ||
|---|---|---|---|---|
Bäume und Wälder
- Eine fuer Anwendungen sehr wichtige Klasse von Graphen sind Bäume.
- In vielen Gebieten wie, z.B beim Compilerbau oder bei Datenbanksystem werden sie haeuftig zur Darstellung von hierarchischen Beziehungen verwendet.
- In diesem Teil werden Anwendungen auf Bäumen besierender Sortieralgorithmus vorgestellt und eine effiziente Realisierung von Vorrang-Warteschlangen diskutiert.
- Ferner werden zwei Algorithmen zur Bestimmung von minimalen aufspannenden Bäumen und ein Verfahren zur Datenkompression beschreiben.
Definition
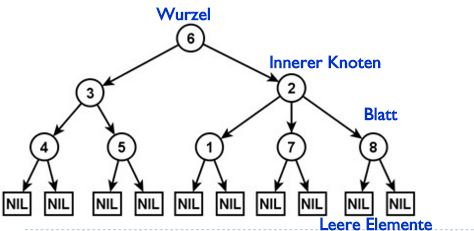
- Ein Baum B ist ein zusammenhängender Graph ohne Kreis. Einen nicht zusammenhängenden Graphen , dessen Zusammenhangskomponenten Bäume sind, nennt man einen Wald.
- Ein Knoten v e V(B) mit d(v) = 1 heißt Blatt.
- Gibt es bei einem gerichteten Baum B einen ausgezeichneten Knoten , von dem aus sämtliche anderen Knoten von B erreichbar sind und der sinerseits von keinem anderen Knoten aus erreicht werden kann. Man nennt diesen Knoten die Wurzel von B und spricht in diesem Fall von einem gewurzelten Baum.
Beispiele
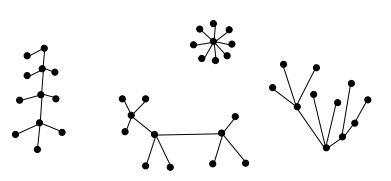
- Die Abbildung zeigt drei Bäume, die zusammen einen Wald bilden. Also einen (ungerichteten) Graph, dessen Zusammenhangskomponenten Bäume sind, wird ein Wald genannt, d.h. jeder kreisfreie Graph ist ein Wald.
- Die folgende Abbildung zeigt einen aus vier Bäumen bestehen Wald.
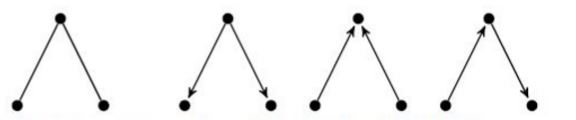
- Bäume mit drei Knoten: ein ungerichteter, drei gerichtete.
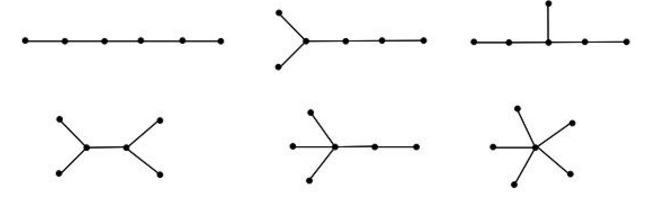
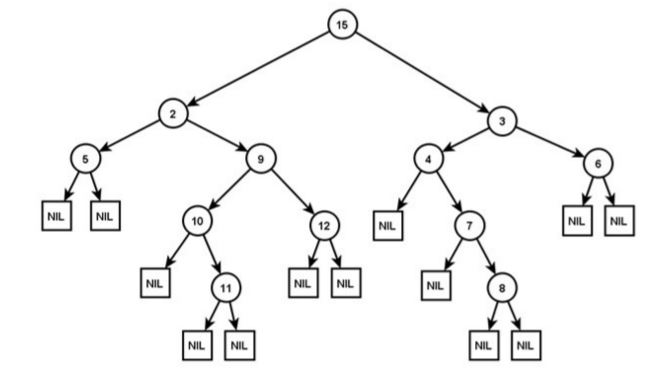
- Die folgende Abbildung zeigt die Liste aller Bäume mit 6 Knoten.
Charakterisierung von Bäumen
Satz: Sei G = (V, E) ein Graph, dann sind die folgenden drei Bedingungen aquivalent:
- G ist ein Baum.
- Je zwei Ecken von G sind durch genau einen Weg verbunden.
- G ist zusammenhängend und |E| = |V| − 1
Anwendung
- Für den Informatiker sind Bäume ein sehr wichtiges Werkzeug.
- Dabei stellt die Tatsache, dass sich eine Reihe praktischer Problemstellungen auf die Konstruktion von aufspannenden Bäumen (bzw. Wäldern)zurückführen lassen, nur einen Teilaspekt des gesamten Anwendungsspektrums dar.
- In der theoretischen Informatik dienen sogenannte Entscheidungsbäume als Modell für Berechnungen.
- Schließlich spielen
Bäume als Datenstruktur für Such- und Sortierprozesse eine wichtige Rolle
Eigenschaften
- Jeder Baum mit Knotenanzahl n > 1 hat mindestens zwei Knoten vom Grad 1 (Blätter). Jeder Baum mit Knotenanzahl n hat Kantenanzahl n − 1.
- Jeder kreislose Graph mit Knotenanzahl n und Kantenanzahl n − 1 ist ein Baum
- Sind u, v zwei verschiedene Knoten in einem Baum T, dann gibt es in T genau einen Weg mit den Endpunkten u und v
Aufspannender Baum und Wald
- Definition: Sei G = (V, E) ungerichtet und zusammenhängend mit |V| = n. Ein Untergraph T auf allen n Knoten, der ein Baum ist, heißt aufspannender Baum von G.
- Analog definiert man einen aufspannenden Wald als Vereinigung von aufspannenden Bäumen von allen Zusammenhangskomponenten eines nichtzusammenhängenden Graphen.
Anzahl ungerichteter Bäume mit n Knoten
- Bäume mit zwei bzw. drei Knoten gibt es ganz sicher jeweils nur einen, wie man sich schnell klar macht.
- Bäume mit vier Knoten gibt es imWesentlichen zwei, Bäume mit fünf Knoten drei verschiedene.
- Für die Anzahl der ungerichteten Bäume mit n Knoten gibt es leider definitiv keine einfache Formel; in Tabelle sind die ersten Anzahlen aufgelistet:
Binärbaum
Ein Binärbaum B ist ein gerichteter (und damit gewurzelter) Baum, bei dem jeder Knoten maximal zwei Nachfolger hat. Ein Binärbaum heißt geordnet, falls jeder innere Knoten einen linken und eventuell einen rechten Nachfolger besitzt (linker Nachfolger muss, rechter
Nachfolger kann). Man bezeichnet einen Binärbaum als voll, wenn jeder Knoten, der kein Blatt ist, genau zwei Nachfolger hat. Ein voller Binärbaum heißt vollständig, wenn alle Blätter die gleiche Tiefe haben.
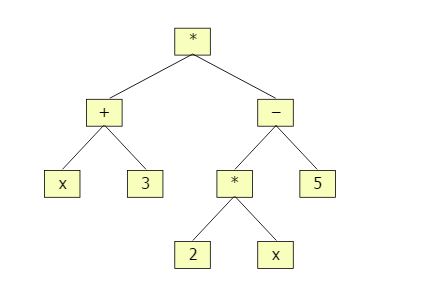
Termbaum
Ein Termbaum dient dazu, einen Rechenterm wie z. B. (x+3)*(2x-5) strukturell zu repräsentieren.
Ziel: Entwicklung eines Programms zur Verarbeitung von Term(bäum)en.
Aufbau Bäume
Bäume Pfad: alle Knoten von einem Knoten k_1 zu einem Knoten k_2 (z. B. 6--> 2--> 8)
Pfadlänge: Anzahl der Knoten von einem Knoten k_1 zu einem Knoten k_2
Tiefe des Baumes: das Maximum aller Pfadlängen von der Wurzel zu einem Blatt
Tiefe eines Knotens: Pfadlänge von der Wurzel zu diesem Knoten
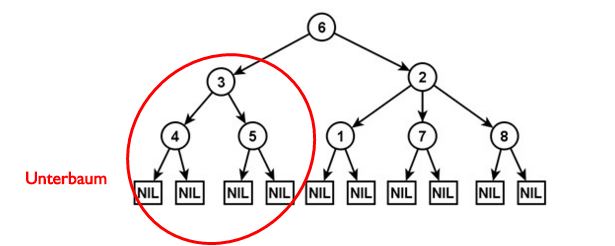
Unterbaum: beliebiger Knoten k mit allen Nachfolgern, k als Wurzel Pfad
Unterbaum
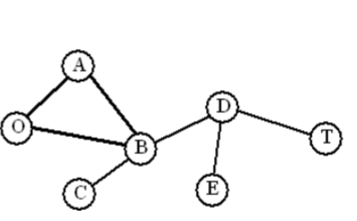
UBUNG
1. Ist diese Graph einen Baum?
Zusammenfassung
Ein Graph besteht aus einer Menge von Knoten und Kanten. Die Knoten tragen Namen und sind durch die Kanten verbunden.
Kann jede Kante eines Graphen in genau einer Richtung durchlaufen werden, so ist der Graph gerichtet.
Ist jeder Kante eines Graphen ein Wert zugewiesen, so ist der Graph gewichtet.
Baum
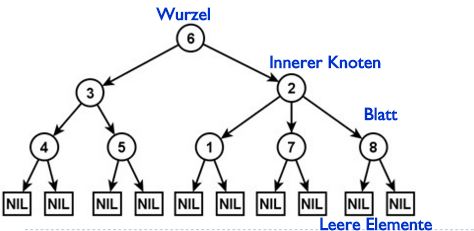
Multigraph: Es kann mehr als eine Kante zwischen denselben Knoten geben.
Existiert für mind. ein Paar (x,y) kein Paar (y,x),so nennt man den Graphen gerichtet.
Bei einem bewerteten Graphen ist jeder Kante ein Wert
zugeordnet.
Existiert für jedes Paar (x,y) auch ein Paar (y,x), so nennt man den Graphen ungerichtet.
Ein (ungerichteter) Graph ist ein Baum, wenn er zusammenhängend ist und keinen Kreis enthält.
Bibliografie
André Krischke, Helge Röpcke - Graphen und Netzwerktheorie
Volker Turau, Algorithmische Graphentheorie
https://de.wikipedia.org/wiki/Graphentheorie
http://www2.cs.uni-paderborn.de/cs/ag-klbue/de/courses/ws09/model/folien/kb-graphen.pdf
http://wvsg.schulen2.regensburg.de/joomla/images/Faecher/Informatik/Informatik_11/informatik_11_3_1_Einfache%20Graphen.html
http://www14.in.tum.de/lehre/2010WS/ds/2011-02-01.pdf
https://www2.informatik.hu-berlin.de/alkox/lehre/lvss03/ti03/vl1507.pdf
http://www.stefan-enderle.de/SS08/GrundlagenDerInformatik-II-3-Graphen.pdf
http://mathworld.wolfram.com/BipartiteGraph.html