Graphen
Aus ProgrammingWiki
Inhaltsverzeichnis |
Motivation und Definition
Die Graphentheorie hat sich seit langem als Teilgebiet der Mathematik etabliert.
Graphen eignen sich hervorragend zur Modellierung realer Systeme und von Prozessen. Die Abbildung von Straßennetzen in Navigationssystemen, von Netzwerken in Routern und Freundschaftsbeziehungen in sozialen Netzen sind nur einige Anwendungsbeispiele. Graphen für Überführungsfunktionen abstrakter Automaten stellen deren Verhalten, wenn Zustandswechsel ausgelöst werden, sehr anschaulich dar.
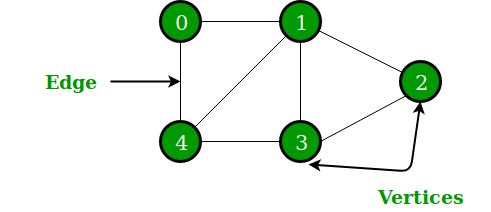
Ein Graph $G=(V,E)$ besteht aus einer Menge $V$ (vertex) von Knoten (Ecken) und einer Menge $E$ (edge) von Kanten, die je zwei adjazente (benachbarte) Knoten verbinden. Eine Kante die die Knoten $i$ und $j$ verbindet, wird als Zweiermenge $\{i, j\}$ bzw. als ein geordnetes Paar $(i, j)$ notiert. Man sagt, eine Kante inzidiert mit den beiden Knoten, die sie verbindet. Prinzipiell sind auch mehrere parallele Kanten zwischen je zwei Knoten und reflexive Kanten (Schlinge: Kante von einem Knoten zu sich selbst) möglich. Diese Formen betrachten wir hier jedoch nicht. Der Grad eines Knotens ergibt sich aus der Anzahl der inzidierenden Kanten.
In der Informatik ist ein Graph ein abstrakter Datentyp (ADT), der die mathematische Definition geeignet abbildet. Im Folgenden werden wir nur Graphen betrachten, die (zwischen zwei beliebigen, nicht notwendigerweise verschiedenen Knoten) keine Mehrfachkanten besitzen.
Arten von Graphen
Ungerichteter Graph
Bei einem ungerichteten Graphen wird die Richtung der Kanten nicht berücksichtigt, d.h. eine Kante $\{i, j\}$ bedeutet eine Direktverbindung vom Knoten $i$ zum Knoten $j$, als auch eine Direktverbindung von $j$ zu $i$. Somit gilt $(i, j) = (j, i)$.
Ein Weg ist eine Knotenfolge, die jeden Knoten aus $|V|$ höchstens einmal enthält.
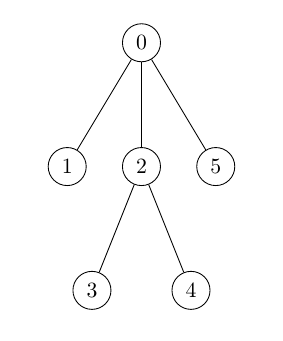
Beispiel: Ungerichteter Graph mit $V = \{0,1,2,3,4\}$ und $E = \{\{0,1\},\{0,4\},\{1,2\},\{1,3\},\{1,4\},\{2,3\},\{3,4\}\}$:
Die Kanten eines ungerichteten Graphen werden als einfache Verbindungslinien, d.h. Strecken oder Bögen zwischen je zwei Knoten, dargestellt.
Gerichteter Graph
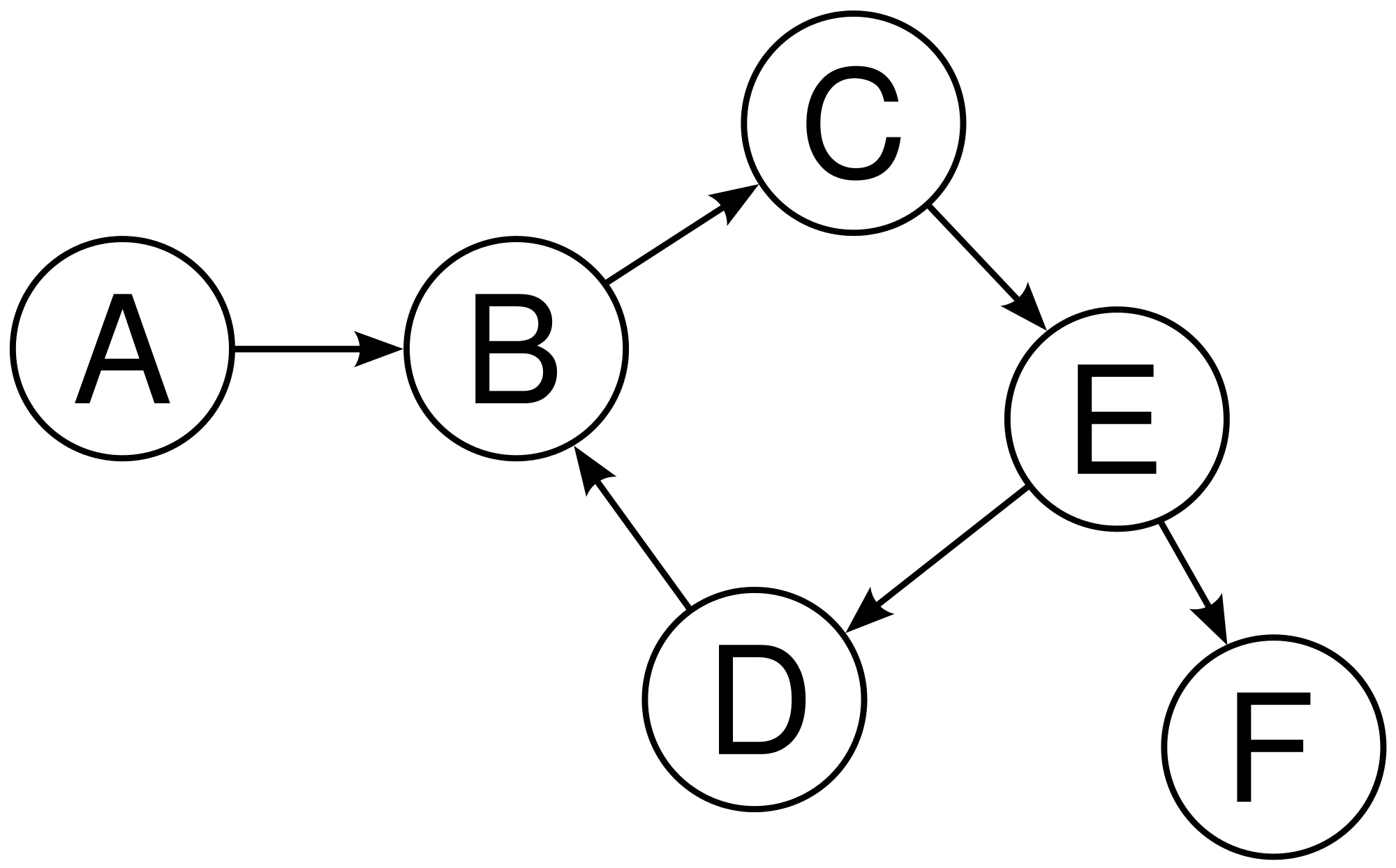
Bei einem gerichteten Graphen wird die Richtung der Kante berücksichtigt und durch einen Pfeil symbolisiert. Eine gegebene Kante $(i, j)$ besagt lediglich, dass es einen Weg von $i$ nach $j$ gibt; nicht automatisch auch von $j$ nach $i$.
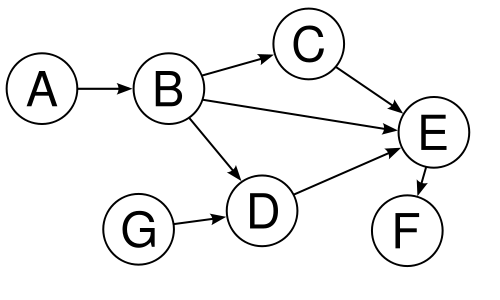
Beispiel: Gerichteter Graph mit $V = \{A,B,C,D,E,F\}$ und $E = \{(A,B),(B,C),(C,E),(D,B),(E,D),(E,F)\}$:
Da eine Kante $\{i, j\}$ in einem ungerichteten Graph durch die beiden Kanten $(i, j)$ und $(j, i)$ in einem gerichteten Graphen dargestellt werden kann, kann jeder ungerichtete Graph in einen äquivalenten gerichteten Graph übertragen werden. Die Umkehrung gilt nicht.
Gewichteter Graph
Bei einem gewichteten Graphen wird jeder Kante ein numerischer Wert als Gewicht zugeordnet. Im Jargon spricht man auch von einem "kantengelabelten" Graphen.
Die Gewichte können dabei jegliche Arten von Kosten darstellen. Dies ist beispielsweise nützlich, um ein Straßennetz abzubilden und mit den Gewichten die Distanz zwischen Knotenpunkten (Städten) anzugeben. Bei einem Navigationssystem könnten auch die benötigte Reisezeit oder der Kraftstoffverbrauch durch die Gewichte ausgedrückt werden.
Ein gewichteter Graph kann sowohl gerichtet, als auch ungerichtet sein.
Repräsentation von Graphen
Adjazenzmatrix
Eine typische Form einen Graphen zu repräsentieren ist die Adjazenzmatrix (Nachbarschaftsmatrix). Dabei handelt es sich um eine quadratische Matrix, deren Zeilen und Spalten den Knoten des Graphen entsprechen. Als konkrete Datenstruktur wird im Allgemeinen ein zweidimensionales Feld verwendet. Die Zeilenknoten interpretiert man als "von"-Knoten und die Spaltenknoten als die "nach"-Knoten. Der in der Matrix im Feld $[i,j]$ eingetragene Wert ist das Gewicht der Kante $(i,j)$. Existiert eine Kante nicht, so wird ein Ersatzwert, wie $\infty$ oder null verwendet. Handelt es sich um einen ungewichteten Graphen, so können auch Booleans oder $0/1$ für die Nicht/Existenz der betrachteten Kante verwendet werden.
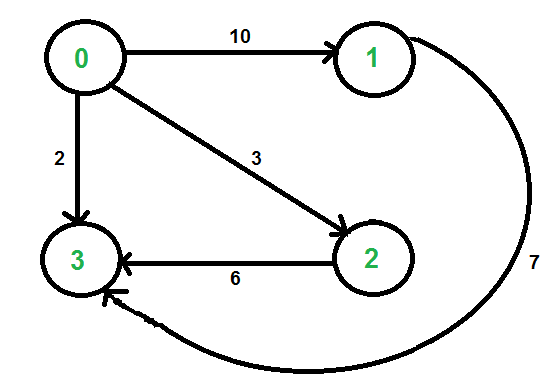
Beispiel: Der Graph
wird folgendermaßen dargestellt:
| von/nach | 0 | 1 | 2 | 3 |
|---|---|---|---|---|
| 0 | 0 | 10 | 3 | 2 |
| 1 | $\infty$ | 0 | $\infty$ | 7 |
| 2 | $\infty$ | $\infty$ | 0 | 6 |
| 3 | $\infty$ | $\infty$ | $\infty$ | 0 |
Zugehörige Adjazenzmatrix: $$ \begin{bmatrix} 0 & 10 & 3 & 2 \\ \infty & 0 & \infty & 7 \\ \infty & \infty & 0 & 6 \\ \infty & \infty & \infty & 0 \\ \end{bmatrix} $$
Da es sich um eine quadratische Matrix handelt, beträgt der Speicheraufwand $\mathcal{O}({\lvert V \rvert}^2)$. $|V|$ steht für die Anzahl der Knoten.
Die Adjazenzmatrix ist als Repräsentationsform ungeeignet, wenn der Graph nur wenige Kanten besitzt, denn dann besteht die Matrix vor allem aus "Blindeinträgen", wie eben $\infty$.
Adjazenzliste
Eine alternative Repräsentation eines Graphen ist die Adjazenzliste: Für jeden Knoten $v$ wir (in einer Liste) vermerkt, mit welchen Knoten $v$ verbunden (adjazent) ist und welches Gewicht die ggf. gerichtete Kante besitzt. Die Elemente der Adjazenzliste sind also `(node, weight)`-Paare. Bei ungewichteten Graphen ist das "Standardgewicht" jeder Kante eine $1$. (Dies kann auch für die Zählung von Niveaus oder Schritten von Vorteil sein.)
Handelt es sich um einen Graphen mit wenigen Kanten, so wird gegenüber einer Adjazenzmatrix weniger Speicherplatz verbraucht, da lediglich für die existierenden Kanten Speicher beansprucht wird. Die Worst-case-Speicherkomplexität beträgt aber ebenfalls $\mathcal{O}({\lvert V \rvert}^2)$, da es bis zu $\lvert V \rvert \cdot \left( \lvert V \rvert - 1 \right) \in \mathcal{O}({\lvert V \rvert}^2)$ Kanten geben kann.
Im Programmbeispiel werden vier Knoten instanziiert. Von v0 aus gibt es gewichtete Kanten zu v1, v2 und v3.
Neben den beiden genannten Repräsentationsformen für Graphen gibt es weitere, die wir hier jedoch nicht betrachten.
Graphalgorithmen
Breadth-First Search (BFS, Breitensuche)
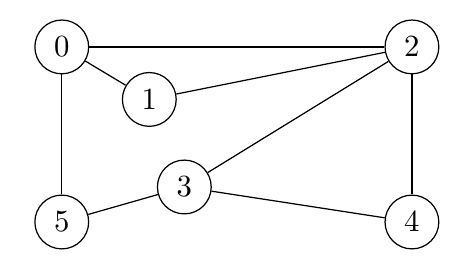
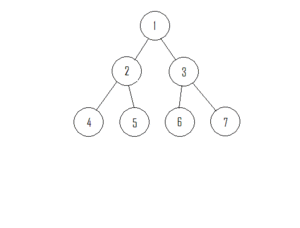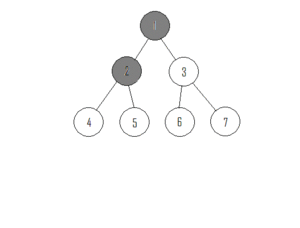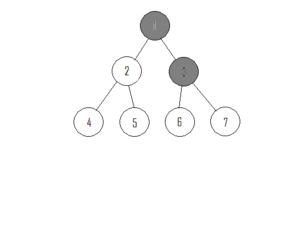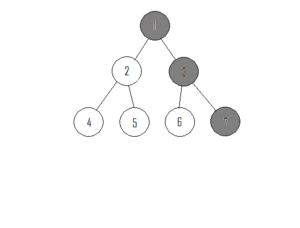
Eine typische Fragestellung für Graphen ist die nach der Erreichbarkeit von Knoten von einem bestimmten Startknoten aus. Dies ist oftmals verbunden mit der Frage nach dem kürzesten Weg vom Start- zum Zielknoten (Single-Source Shortest Path). Bei ungewichteten Graphen entspricht die Entfernung vom Start- zum Zielknoten der Anzahl der auf dem Weg liegenden Kanten. In folgendem Beispiel ist 2 die geringste Entfernung von Knoten 4 vom Startknoten 0, wegen $(0,2,4)$, nicht etwa 3, wegen $(0,5,3,4)$, oder 4, wegen $(0,5,3,2,4)$ bzw. $(0,1,2,3,4)$.
Beispiel: Wir starten im Knoten mit der Bezeichnung 0 des folgenden Graphen.
Die klassische Breitensuche (BFS) bildet die Grundlage für eine Reihe von Algorithmen zur Verarbeitung von Graphen. Bei der Breitensuche in einem ungewichteten Graphen wird - anders als bei der weiter unten betrachteten Tiefensuche (Depth-First Search, DFS) - gleichmäßig vom Wurzelknoten (der Knoten, bei dem der gesuchte Pfad beginnt) aus vorwärts gegangen. "Gleichmäßig" bedeutet dabei, dass, bevor man weiter in die Tiefe des Graphen voran schreitet, zunächst alle Knoten einer Ebene festgestellt werden. Zwei Knoten sind dabei auf der gleichen Ebene, wenn sie gleich weit, d.h. um die gleiche Anzahl an Knoten, vom Wurzelknoten entfernt sind.
Wenn wir nach den kürzesten Wegen zu den Knoten eines Graphen vom Wurzelknoten aus fragen, ist sofort einzusehen, dass wir Kreise ausschließen müssen. Ein Weg (geschlossener Kantenzug), der außer dem Anfangs- und Endknoten jeden seiner Knoten nur einmal durchläuft, heißt Kreis. Im Beispielgraphen sind $(0,5,3,4,2,0)$ und $(0,5,3,2,0)$ solche Kreise. Wie im Kreisverkehr führt jede weitere Runde zurück zum Ausgangspunkt und macht die gefahrene Strecke nur länger. Wir müssen daher vermeiden, dass bereits besuchte Knoten erneut betreten/betrachtet werden. Diese "Erinnerung" erreicht man mit Markierungen.
Wir gehen folgendermaßen vor: 1. Wähle einen Startknoten, markiere ihn und schreibe ihn in eine Liste. 2. Streiche den ersten Knoten aus der Liste und nenne ihn aktiver Knoten. 3. Markiere alle noch nicht markierten Nachbarn des aktiven Knotens. Vermerke für alle nun markierten Nachbarn den aktiven Knoten als Vorgängerknoten (auf dem Weg zum Ziel). 4. Füge die neu markierten Knoten in der Liste (hinten) an. 5. Falls die Liste leer ist, dann Stopp, sonst weiter bei 2.
Wie man sieht, ist das BFS-Verfahren nicht rekursiv und es gibt auch kein Backtracking.
Die in den Schritten 2 und 4 angewandten Operationen (dequeue und enqueue) sind charakteristisch für Warteschlangen. Das Verarbeitungsprinzip heißt FIFO = First-In-First-Out: Wer am Anfang einer Warteschlange steht, wird zuerst bedient; wer (irgendwann) bedient werden möchte, muss sich hinten anstellen. Eine dem entsprechende Datenstruktur nennt man Queue. Sie ist in allen gängigen Programmiersprachen implementiert. In Python heißen die zugehörigen Methoden `put(node)` und `get()`.
Zur Erfassung des jeweiligen Vorgängerknotens wird im Programm eine Datenstruktur verwendet, die man Dictionary nennt. Wir betrachten sie im Zusammenhang mit dem Thema Hashing etwas genauer. Es handelt sich um eine Menge von key-value-Paaren beliebigen Datentyps. Der zu einem Schlüssel (key) gehörende Wert (value) wird durch Angabe dieses Schlüssels (sehr effizient) gefunden. Ob eine bestimmte Eingabe tatsächlich ein Schlüssel ist, kann abgefragt werden:
In der folgenden Funktion `bfs` sind sowohl die Schlüssel als auch die Werte des Dictionarys `pred` Knoten des betrachteten Graphen. Der Eintrag des Vorgängerknotens in das Dictionary wird mit der Markierung des betrachteten Knotens verbunden, was genau dem Schritt 3 entspricht. Ein besuchter Knoten wird also dadurch markiert, dass er in der Dictionary erstmals erfasst wird.
Aus diesen Angaben kann der BFS-Suchbaum für dieses Beispiel sehr einfach rekonstruiert werden. Jeder Knoten des Baumes besitzt genau einen Vorgänger.
Single-Source Shortest Path (SSSP)
Um in einem ungewichteten Graphen (bzw. in einem gewichteten Graphen, bei dem alle Kanten das gleiche Gewicht haben) den kürzesten Weg von einem Quellknoten zu einem vorgegebenen Knoten zu finden, kann die Breitensuche verwendet werden. Da die Breitensuche gleichmäßig von Ebene zu Ebene expandiert, muss man während des BFS-Prozesses lediglich mitzählen, in welcher Ebene man sich befindet. Die Ebene gibt an, wie weit der jeweils gefundene Knoten vom Quellknoten entfernt ist (Anzahl der Kanten auf dem Pfad).
Mit Hilfe des folgenden Programms können wir die Aussage zum kürzesten Weg (2) von Knoten 0 (a) zum Knoten 4 (e) für unser obiges Beispiel vom Beginn des Abschnitts überprüfen. Die BFS als Basisprozesse ist deutlich erkennbar.
Depth-First Search (DFS, Tiefensuche)
Eine BFS (in dieser Grundform) besucht für jeden Knoten alle Nachbarknoten des (zusammenhängenden) Graphen und setzt die Suche für diese entsprechend fort. Dies ist zwar sehr systematisch und für viele Aufgabenstellungen angemessen, kann aber in bestimmten Fällen aufwendiger sein.
Ein klassisches Beispiel ist das Labyrinthproblem. Um von einem Startknoten (Eingang) aus den in einem (unbekannten) Zielknoten (Versteck) hinterlegten Schatz zu finden, ist eine systematische Suche erforderlich. Dafür hat sich (schon in der Antike) folgendes Verfahren herauskristallisiert: Markiere jede besuchte Kreuzung (Punkt mit mehreren Straßenabzweigungen) und setze die Suche bei einer der Folgekreuzungen fort. Gibt es an einer solchen keine unmarkierten Fortsetzungsmöglichkeiten, so gehe zurück zum letzten Entscheidungspunkt und wähle eine noch unmarkierte Folgekreuzung.
Diese Verfahren schreitet zuerst in die Tiefe des Suchbaums voran, nicht in die Breite, wie bei BFS. Es kann effizienter sein, da es viele Fortsetzungsmöglichkeiten unbetrachtet lässt. Im worst case muss dennoch der vollständige Suchbaum aufgebaut werden.
Nach dieser intuitiven Einführung können wir nun das Verfahren auf einer abstrakteren Basis mit Graphen präsentieren.
Die Depth-First Search (Tiefensuche) beginnt bei einem festgelegten Startknoten. Für jeden der zu diesem Startknoten adjazenten Knoten wird im Folgenden die Tiefensuche rekursiv durchgeführt. Man beginnt mit dem ersten dieser adjazenten Knoten und schreitet in die Tiefe (auf das nächste Niveau) rekursiv fort. Dies wird solange fortgesetzt, bis ein Knoten erreicht ist, der keine unbearbeiteten adjazenten Knoten hat. Die Rekursion sorgt dann automatisch dafür, dass zum letzten ausgewählten und nun vollständig bearbeiteten Knoten zurückgegangen wird. Die Fortsetzung erfolgt dort, wo die nächste Entscheidungsmöglichkeit besteht, d.h. beim nächsten adjazenten Knoten: Backtracking.
Der beschriebene Prozess kann mit Hilfe eines Stacks (ADT) adäquat implementiert werden. Ein Stack arbeitet nach dem LIFO-Prinzip: Last-in-first out: Das Element, das als letztes auf den Stack gelegt wurde, wird zuerst entfernt. Wie oben beschrieben, wird die Stackarbeit auf der Ebene der Programmiersprache durch die Verarbeitug rekursiver Prozeduren erledigt.
In folgendem Beispiel könnten Knotenvergleiche, die zur Elementsuche notwendig wären, leicht hinzugefügt werden.
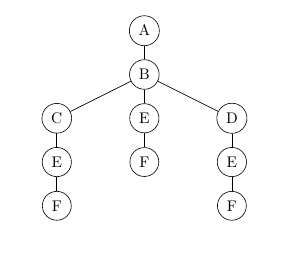
Beispiel:
Da die Reihenfolge, in der die zu B adjazenten Knoten C, E und D angegeben sind, für das Verfahren eine (gewisse) Rolle spielt, fragen wir danach:
Nun können wir das DFS-Verfahren knapp und elegant rekursiv implementieren:
Es lohnt sich ein Ablaufprotokoll in Kurzform, A bedeutet dfs(A), anzufertigen:
Die angegebenen Knoten werden unmittelbar nachdem sie das erste Mal besucht wurden, gedruckt. Fahren Sie mit dem Finger den Baum entlang und notieren Sie die jeweils erste (von jeweils drei) Knotenberührung(en). dfs(A) erfordert dfs(B). Die Berechnung erfordert (bei oben ergründeter Reihenfolge der Adjazenzknoten $C, E, D$) dfs(C). Daraus ergibt sich dfs(E) und schließlich dfs(F). Da $F$ keinen Folgeknoten besitzt, liefert mehrfaches Backtracking die Fortsetzung bei dfs(E), was wiederum dfs(F) aufruft. Der letzte Versuch findet mit dfs(D) statt, was wiederum dfs(E) und weiter dfs(F) berechnet. Es schließt sich mehrfaches Backtracking an, bis das Ausgangsniveau von $A$ wieder erreicht ist.
Es werden alle von A aus erreichbaren Knoten ausgegeben, entsprechend der Reihenfolge von DFS: Im Baum jeweils die erste Knotenberührung. Der Knoten $G$ taucht nicht auf, da er von $A$ aus nicht erreichbar ist.
Da es mehrere Wege zu einem Knoten gibt, kommen Knoten mehrfach vor. Handelt es sich um einen Graphen mit Kreisen bzw. Zyklen, so würde der Algorithmus nicht terminieren. Dies illustrieren wir an obigem Beispiel, indem wir eine Kante von $F$ nach $G$ hinzufügen, sodass mehrere Zyklen entstehen. (Es empfiehlt sich nach dem Experiment, die Kante wieder herauszukommentieren und alle Felder des Notebooks neu zu evaluieren.)
Um dies zu verhindern, kann man (z.B. in einem Dictionary) die bereits gefundenen Knoten speichern und den jeweils nächsten nur dann besuchen, wenn er vorher noch nicht betreten wurde. Dies vereinfacht auch die DFS in unserem obigen (zyklenfreien) Beispiel, wenn z.B. dfs(E) nicht mehrfach berechnet werden muss.
Es folgt noch eine zweite Variante `dfs3`, die anstelle des Dictionarys für die markierten Knoten eine Menge verwendet. Man beachte, dass beide Funktionen zwar nicht in einen Endloszyklus hineinlaufen, wenn der Graph nicht zyklenfrei ist. Eine Vorabentscheidung, ob ein gegebener Graph einen Zyklus besitzt oder nicht, können sie beide nicht treffen. Wir geben sie an, weil daraus die Funktion `dfs_erreichbar` unmittelbar abgeleitet werden kann.
Alternativ ist es möglich, einen noch unbetrachteten Knoten weiß, einen noch nicht vollständig einbezogenen grau und einen vollständig berücksichtigten schwarz zu färben.
Da jeder Knoten und jede Kante jeweils maximal einmal besucht werden, beträgt die Laufzeit $\mathcal{O}(\lvert V \rvert + \lvert E \rvert)$. Handelt es sich um einen zusammenhängenden Graphen gilt $|E|\geq |V|-1$, sodass man den Aufwand mit $\mathcal{O}(|E|)$ abschätzen kann.
Die Graphentheorie definiert eine große Palette von Eigenschaften, die ein Graph besitzt oder nicht. Darunter gibt es Eigenschaften, die für die Informatik von besonderer Bedeutung sind, weil sie Standardfälle der Modellierung darstellen.
Erreichbarkeit
Ein Knoten $w$ eines (gerichteten oder ungerichteten) Graphen heißt von $v$ erreichbar, wenn es einen Weg von $v$ nach $w$ gibt. Wir bestimmen die Menge der von $v$ erreichbaren Knoten. Wie weiter oben angekündigt entwickeln wir `dfs_erreichbar` aus `dfs3` heraus, indem wir auf die Ausgabe der besuchten Knoten verzichten und sie in einer Menge zusammenfassen. Man beachte, dass Mengen ungeordnete Zusammenfassungen von Elementen sind. Das Aufrufbeispiel zeigt beispielsweise, dass die Knoten $A,B$ und $C$ von $G$ nicht erreichbar sind.
Zusammenhängender ungerichteter Graph
Ein ungerichteter Graph ist zusammenhängend, wenn jeder Knoten mit jedem anderen durch einen Weg (Pfad, Kantenzug) verbunden ist. Ein Weg wird als Folge der zugehörigen Knoten, die durch Kanten verbunden sind, angegeben. Die Länge eines Weges ergibt sich aus der Anzahl der darin vorkommenden Kanten.
In einem zusammenhängenden Graphen muss jeder Knoten von jedem Knoten erreichbar sein. Dies können wir mit `dfs_erreichbar` feststellen. Besteht ein Graph aus mehreren nicht zusammenhängenden Teilen, so nennt man diese Zusammenhangskomponenten.
Für das obige Beispiel eines gerichteten Graphen ergänzen wir die jeweilige gerichtete Kante in Gegenrichtung, um einen de facto ungerichteten Graphen zu erhalten.
Entfernt man beispielsweise die gerichtete Kante von $F$ nach $E$, können von $F$ aus keine Knoten erreicht werden.
Gerichteter zyklenfreier Graph (DAG)
Häufig werden gerichtete Graphen (Digraphen) verwendet, die keinen Zyklus besitzen dürfen. Man nennt sie DAG (directed acyclic graph). Einen Weg $(v_1,v_2,\ldots,v_m)$, bei dem der Start- $v_1$ mit dem Endknoten $v_m$ übereinstimmt, nennt man Zyklus. Wenn dies der einzige wiederholte Knoten in der Knotenfolge ist, heißt er Kreis. Ein Zyklus ist nicht identisch mit einer Schleife/Schlinge, also einer reflexiven Kante $(v,v)$ zum gleichen Knoten in einem gerichteten Graphen.
Ein typisches Beispiel für die Anwendung von DAGs sind Ablaufplanungen mit Vorrangbedingungen. Als solche sind sie in vielen Bereichen (Haushalt, Produktion, Finanzplanung usw.) anzutreffen. Studierende können die Wahl der Vorlesungen von fachlichen Voraussetzungen, wie sie in einem Modulhandbuch hinterlegt sind, abhängig machen. Auf diese Weise kann eine studierbare Sequenz aufeinander aufbauender Module zusammengestellt werden.
Eine von Knoten $A$ zu Knoten $B$ zeigende Kante drückt aus, dass Vorlesung $B$ erst dann gehört werden sollte, wenn der betreffende Studierende den Inhalt aus Vorlesung $A$ aufgenommen hat. Ein nach dieser Vorgehensweise modellierter Graph besteht also aus einer unvollständig geordneten Knotenmenge, denn nicht jedes Knotenpaar gehört zu einer solchen Voraussetzungsrelation. Mit Hilfe des topologischen Sortierens wird daraus eine vollständige Ordnung hergestellt. "Hält man" einen bestimmten Knoten fest, so zeigen sämtliche Kanten nach unten und drücken die Abhängigkeits(richtung) aus.
Ist dies an einer oder mehreren Stellen verletzt, sodass auch Aufwärtskanten vorkommen, liegt ein Fehler vor. Der Digraph ist dann nicht zyklenfrei, also kein DAG. Da Graphen im Allgemeinen sehr viele Knoten, Kanten und damit Zyklen haben können, lautet die Grundaufgabe der Zykluserkennung: Besitzt der vorgelegte Digraph (mind.) einen Zyklus? (Aufgrund der gegebenen Anwendungsbreite beschränken wir unsere Betrachtung auf Digraphen, obwohl Zyklen auch in ungerichteten Graphen auftreten können.)
Wir entwickeln die Lösung auf der Basis einer Tiefensuche (DFS). Die Stack-Verwaltung bei der Ausführung der rekursiven DFS-Funktion wirkt wie der ausgerollte Faden zur Rückkehr zum Eingang des Labyrinths: Wir finden den Weg von $w$ zum Eingang $v$ zurück, indem wir der Knotensequenz beim Abbau des Stacks folgen. Es gibt also einen Weg von $w$ nach $v$. So interpretieren wir den Stack-Inhalt $w=F,E,C,B,v=A$ (top of stack ist links) für den aktuellen Weg, der mit dem Knoten $v=A$ beginnt und in der Folge die Knoten $B, C, E$ und $F$ besucht. Finden wir nun eine gerichtete Kante von $v$ zu irgendeinem dieser auf dem Weg liegenden Knoten $w$, so liegt ein Zyklus vor, denn diese Kante vervollständigt den Zyklus.
Vor dem Aufruf (beider Funktionen) fügen wir obigem DAG noch die gerichtete Kante von $D$ zu $A$ hinzu, sodass Zyklen entstehen. Die ansonsten hinzugefügten Kanten zur Herstellung eines zugehörigen ungerichteten Graphen, müssen wieder entfernt werden: Herauskommentieren der Kanten.
Für die Startknoten $A$, $B$, $D$ und $G$ werden Zyklen gefunden, für die übrigen Knoten nicht. Fazit: Der vorliegende Graph mit Kante von $D$ nach $A$ ist kein DAG! Die Komplexität des Verfahrens entspricht der von DFS.
Alternative Überlegung: Bei der Tiefensuche in einem Graphen kann es drei verschiedene Arten von Kanten geben: Vorwärts-, Quer- und Rückwärtskanten. Nur Rückwärtskanten, die auf Knoten zeigen, die sich noch in Bearbeitung befinden, d.h. die besucht aber noch nicht verlassen wurden, bilden Zyklen. Taschenbuch der Algorithmen, S. 86ff
Hinweis: Die Schleifensuche in einfach verketteten Listen kann mit dem Hase-Igel-Algorithmus mit linearem Aufwand $\mathcal{O}(n)$ bewerkstelligt werden. Das Verfahren ist nicht mit dem Floyd-Warshall-Algorithmus zur Bestimmung der kürzesten Wege für alle Knotenpaare zu verwechseln!
Baum
Ist ein gegebener Graph ein Baum? Dies können wir unter Verwendung der oben bereitgestellten Verfahren entscheiden. Ein Baum ist ein ungerichteter azyklischer zusammenhängender Graph. Ein Wurzelbaum ist ein Baum mit einem als Wurzel markierten Knoten.
Ein aufspannender Baum eines zusammenhängenden Graphen ist ein Baum, d.h. ein kreisfreier und zusammenhängender Teilgraph $G'=(V',E')$, mit $V'=V$ und $E'\subseteq E$. kreisfrei bedeutet eine Knotenfolge ohne Knotenwiederholung.
Ein Graph, der selbst ein aufspannender Baum ist, heißt Baum. In einem Baum sind je zwei Knoten durch genau einen Weg miteinander verbunden.
Anwendungsbeispiel: 0/1-Rucksackproblem
Beim Rucksackproblem ist eine nichtleere Menge von $n$ Gegenständen mit den Gewichten (weight) $w_1, w_2, \dotsc, w_n$ mit $w_i > 0$ und den zugehörigen Werten (value) $v_1, v_2, \dotsc, v_n$ mit $v_i>0$ gegeben. Das Gewicht des $i$-ten Gegenstands beträgt $w_i$, dessen Wert ist $v_i$.
Die Interpretation des Wertes wird durch den jeweiligen Sachkontext bestimmt: Denkt man an Schmuck, so kann der Wert im potenziellen Verkaufserlös bestehen. Handelt es sich um Utensilien eines Bergwanderes, richtet sich der Wert eines Gegenstandes eher nach dessen Beitrag zur Absicherung einer unfallfreien Begehung.
Der Rucksack ist nur beschränkt belastbar. Das zulässige Maximalgewicht sei $K$, d.h. das aktuelle Gesamtgewicht darf $K$ keinesfalls überschreiten. Zu beachten ist, dass beim 0/1-Rucksackproblem, im Gegansatz zum Bruchteil-Rucksackproblem, ein Gegenstand entweder in den Rucksack gepackt werden kann oder nicht, eine Teilung des Gegenstands und anteilige Mitnahme sind bei "0/1" nicht möglich.
Die Optimierungsaufgabe besteht nun darin, einen Rucksack so zu füllen, dass die Wertsumme der eingepackten Gegenstände – unter Beachtung der Kapazitätsbeschränkung des Rucksacks – maximal ist.
Zum Finden der Lösungen dieses Problems unter Nutzung der Tiefensuche
muss ein Entscheidungsbaum (ungerichteter, azyklischer und zusammenhängender Graph) aufgestellt werden. In jedem Schritt gibt es für jedes aktuelle Blatt genau eine Ja/Nein-Entscheidung, d.h. zwei Möglichkeiten (Binärbaum): entweder wird der $i$-te Gegenstand in den Rucksack gepackt oder nicht. Der Entscheidungsbaum hat folglich die Höhe $n$ ($n$ = Anzahl der Gegenstände). Die Wurzel repräsentiert den anfangs leeren Rucksack. Sie liegt auf Niveau $0$ des Baumes. Die Blätter des Baums auf Niveau $n$ repräsentieren alle Gegenstandskombinationen der Rucksackbefüllung.
Der Entscheidungsbaum liegt nicht als Datenstruktur vor, sondern stellt das Aufbauschema für die Rucksackbefüllungen dar. Man kann es sich als ein Protokoll der Berechnung aller Möglichkeiten vorstellen. Diese Berechnung kann systematisch mit Tiefensuche vorgenommen werden.
Da es sich um einen Binärbaum handelt, beträgt die Anzahl der Bätter höchstens $2^n$. Insgesamt besteht der Baum aus $\sum_{i=0}^n 2^i = 2^{n+1} - 1 \in \mathcal{O}(2^n)$ Knoten. Die Laufzeit des Algorithmus' liegt folglich in $\mathcal{O}(2^n)$. Zur Ermittlung aller infrage kommenden Packvarianten (Blätter) ist ein exponentieller Zeitaufwand erforderlich.
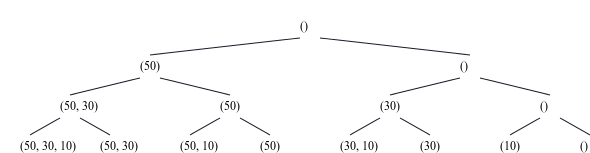
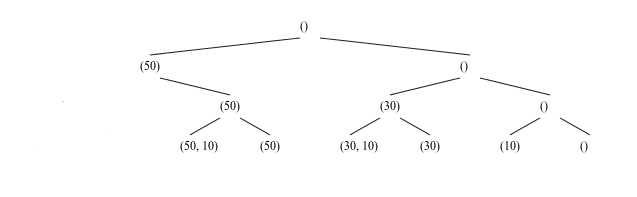
Beispiel: Für drei Gegenstände ($n=3$) mit den Gewichten 50 (Wert: 30), 30 (Wert: 20) und 10 (Wert: 25) ergibt sich der folgende Entscheidungsbaum. (Die Reihenfolge der Gegenstände in der Liste spielt dabei keine Rolle.)
Wie erwartet besitzt der Baum $2^3=8$ Blätter.
Mit knapsack_dfs wird die gesamte Knotenfolgenfolge bei zugrunde liegender Tiefensuche (unbeschränkter DFS-Durchlauf) aufgelistet. Sie kann im Graph sehr gut nachvollzogen werden (Backtracking).
Die Blätter des Baumes sind in der Ausgabe (print) mit Rucksack: eingeleitet. Danach folgt die Angabe der eingepackten Gegenstände als Liste von Gewicht-Wert-Paaren, wohingegen die Gegenstände in der Knotennotation nur mit ihrem Gewicht angegeben werden. Mehrere Gegenstände bilden eine Liste ihrer Gewichte. Diese einfache Notation muss für Beispiele mit gewichtsgleichen Gegenständen verändert werden.
Als Nächstes wird die Kapazitätsbeschränkung des Rucksacks einbezogen. Hierfür muss gegenüber knapsack_dfs lediglich eine Programmzeile eingefügt werden: Die Mitnahme eines Gegenstandes findet grundsätzlich nur dann statt, wenn er noch in den Rucksack passt, d.h. wenn dessen Gewicht die aktuelle Restkapazität des Rucksacks nicht überschreitet: items[0][0] <= k.
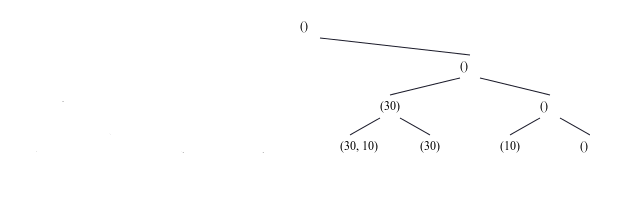
Für $K=62$ wird die Zahl der Knoten (zulässige Rucksackbefüllungen) reduziert:
Für $K=41$ wird der ursprünglich vollständige Binärbaum noch mehr reduziert.
An der exponentiellen Aufwandsordnung ändert sich jedoch nichts.
Nachdem sämtliche Rucksackbelegungen (Blätter), die die Gewichtsbeschränkung respektieren, gefunden wurden, bestimmen wir deren Gesamtwerte durch Summieren der Einzelwerte und ermitteln die Belegung(en) mit dem Maximalwert.
Die Modifikation von knapsack_dfs_ltd sind geringfügig: Die gültigen Belegungen werden in der mit validKnapsacks bezeichneten Liste gesammelt.
Um zu demonstrieren, dass es mehrere Packmöglichkeiten mit einem maximalen Gesamtwert geben kann, verwenden wir die folgenden drei Gegenstände: 50 (Wert: 45), 30 (Wert: 20), 10 (Wert: 25) bei einer Gewichtsbeschränkung auf $K=52$.
Im Beispiel sind prinzipiell 5 Rucksackbelegungen möglich aber nur zwei davon, nämlich [50] (Wert: 45) und [30, 10] (Wert: 20+25=45), erzielen den Maximalwert in Höhe von 45.
Anwendungsbeispiel: n-Damenproblem
Das $n$-Damenproblem ist ein schachmathematisches Problem und eine Verallgemeinerung des 8-Damenproblems.
Die Aufgabe besteht darin, 8 Damen auf einem $8\times 8$-Schachbrett so zu platzieren, dass keine Dame gemäß den Schachregeln eine andere Dame bedroht, d.h. schlagen kann. Dies bedeutet, dass keine zwei Damen auf der selben Linie (a-h), Reihe (1-8) oder Diagonale stehen dürfen. Im Unterschied zur Begrifflichkeit im Schach gehen wir hier von einer Matrixgestalt aus und bezeichnen die Zeilen und Spalten mit $0, 1, \ldots, 7$. Es spielt auch keine Rolle, ob das Feld rechts unten ein weißes ist. Im Schach wäre das Pflicht.
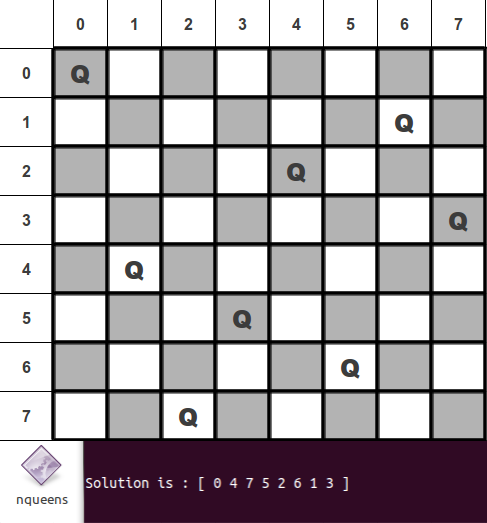
Eine Lösung für das 8-Dameproblem ist die folgende:
Das 8-Damenproblem lässt sich sinngemäß auf ein $n$-Damenproblem ausweiten, d.h. $n$ Damen sollen bedrohungsfrei auf einem $n\times n$-Schachbrett platziert werden.
Zur Lösung dieses Problems kann ebenfalls Depth-First-Search eingesetzt werden.
Dabei nutzen wir eine Liste mit bis zu $n$-Elementen als Datenstruktur, die am Index $i$ angibt, in welcher Zeile in der $i$-ten Spalte eine Dame platziert wurde. Aufgrund der Tatsache, dass eine Dame ihre komplette Spalte schlägt, ist es trivial, dass sich in jeder Spalte nur höchstens eine Dame befinden kann. Da $n$ Damen auf $n$ Reihen verteilt werden, folgt, dass in jeder Spalte genau eine Dame stehen muss.
Die Liste [0, 4, 7, 5, 2, 6, 1, 3] beschreibt folgende Stellung:
Sie repräsentiert eine Lösung. Dies kann man leicht überprüfen. Uns geht es jedoch um einen Algorithmus zum Finden einer solchen Stellung. Ergänzend fragt man sich natürlich, wie viele Lösungen es für ein gegebenes $n$ gibt.
Man beginnt mit einem leeren Schachbrett -- dies wird durch eine leere Liste repräsentiert. Nun soll schrittweise in jeder Spalte eine Dame platziert werden. Dabei werden alle Zeilen von 0 bis $n-1$ systematisch durchprobiert. Dies bedeutet, dass $n$-mal die Tiefensuche mit der entsprechenden Konfiguration aufgerufen wird. Es wird dabei geprüft, ob es sich bei der angegebenen Stellung noch um eine gültige Stellung handelt, d.h. keine Dame kann eine andere Dame schlagen. Ist dies der Fall, so wird der Algorithmus für die nächste Spalte mit den Zeilen 0 bis $n-1$ rekursiv aufgerufen. Handelt es sich nicht um eine gültige Stellung, so wird eine leere Liste als Lösungsmenge zurückgegeben und ein Backtracking ausgeführt: Rückkehr zum letzten Entscheidungspunkt. Dieser Ablauf wird vollständig durch die rekursive Natur von DFS gesteuert.
Die hier beschriebene DFS minimiert die Anzahl der zu überprüfenden Stellungen enorm, da - im Gegensatz zu einem Brute-Force-Ansatz, bei dem alle Stellungen durchprobiert werden - nun auch die jeweils folgenden Stellungen ausgeschlossen werden.
Rucksack- und $n$-Damenproblem sind zwei klassische Problemstellungen, die mit DFS oftmals effizienter gelöst werden können als mit Brute-Force-Ansatz. Im schlechtesten Fall muss dennoch der gesamte Baum traversiert werden. Dies führt zu exponentiellem Aufwand. Bis heute sieht es so aus, als ob es kein Verfahren gibt, dass diese Problemstellungen besser als mit exponentiellem Aufwand (exakt) löst.