Hashing und Hash-Tables
Aus ProgrammingWiki
Inhaltsverzeichnis |
Motivation
Anwendungsfall "Produktkosten im Supermarkt"
Statt in einer langen Liste nach Produkten und deren zugehörigen Preisen nachzuschauen, wie viel ein Kunde für den ausgewählten Artikel zu bezahlen hat, fragt man eine Angestellte, die das alles weiß.
Anwendungsfall "Memoizing"
Rekursive Berechnungen können sehr aufwendig sein. Dies sieht man am Beispiel der Fibonacci-Zahlen, wo üppige Teilbäume mehrfach berechnet werden. Dies kann durch Memoizing vermieden werden.
Die Idee von Memoizing lautet: Prüfe zuerst, ob der Wert des zu berechnenden Ausdrucks bereits vorliegt. Ist dies der Fall, so verwende dieses Resultat. Anderenfalls ermittle den zugehörigen Wert durch Berechnung und speichere ihn für spätere Verwendung(en).
Anwendungsfall "Wählerliste"
Bei Wahlverfahren wird zuerst festgestellt, ob ein (mit Personalausweis identifizierbarer) Wahlbenachrichtigter tatsächlich wahlberechtigt ist. Hierfür wird geprüft,
- ob der Name dieser Person im Wählerverzeichnis steht und
- ob diese Person noch nicht gewählt hat.
Ist das der Fall, schließt sich der entsprechende Wahlvorgang an.
Die Wahlhelfer könnten für diese Prüfung das Verfahren der linearen Suche anwenden: Sie beginnen beim ersten Namenseintrag im Wählerverzeichnis und vergleichen diesen Namen mit dem der zu überprüfenden Person. Markierte Listenelemente, d.h. die Namen der Bürger, die ihre Stimmen bereits abgegeben haben, werden übergangen. Im ungünstigsten Fall steht der gesuchte Name am Ende der Liste mit $n$ Elementen, sodass sich ein Aufwand von $\mathcal{O}(n)$ ergibt. Nicht zu unterschätzen ist der Aufwand $K$ für jeweils einen Namensvergleich, z.B. für Sabine Leutheusser-Schnarrenberger (deutsche Politikerin) oder für zu scannende Passbilder. $K$ lässt sich durch eine Konstante nach oben abschätzen, sodass es trotz $\mathcal{O}(n\cdot K)$ bei $\mathcal{O}(n)$ bleibt.
Ein linearer Aufwand für die Suche im schlechtesten Fall ist ein sehr guter Wert, führt aber für große $n$ dennoch zu erheblichen Wartezeiten. Der Aufwand lässt sich verringern, wenn das Wählerverzeichnis nach Namen sortiert vorliegt. Der dafür erforderliche Sortieraufwand fällt genau einmal an, nämlich vor dem o.g. Prüfprozess. Verwendet man anschließend die sehr effiziente binäre Suche, so ergibt sich ein Aufwand in $\mathcal{O}(\log{}n)$.
Eine noch bessere Effizienz kann man nur erzielen, wenn man sich grundsätzlich vom Suchprozess verabschiedet: Wir stellen uns vor, dass jemand alle Wählerinnen und Wähler kennt und über deren Teilnahme am Wahlvorgang Bescheid weiß. Diese Person brauchen wir dann nur zu fragen, ob die betreffende Bürgerin wahlberechtigt ist oder nicht. Der dafür erforderliche Aufwand ist konstant, d.h. unabhängig von $n$ in $\mathcal{O}(1)$.
Anstelle die Position eines Listenelements zu suchen, wird die zugehörige Adresse berechnet. Statt einer Liste verwenden wir dafür eine sog. Hashtabelle (hashtable, hashmap, dictionary, assoziative Datenfelder).
ADT-Dictionary
Hashing ist eine Methode zur Datenverwaltung, bei der die Datensätze über einen Schlüssel (key) angesprochen werden. Statt Datensätze durch Vergleiche ihrer Schlüssel zu suchen, geschieht dies beim Hashing (to hash = klein zerhacken) durch Berechnung der Adressen (Indizes) von Zeigern, die auf die zugehörigen Datensätze zeigen. Die Zeiger bilden die Einträge in einem Feld (hashtable).
Die drei Dictionary-Operationen (Einfügen, Suchen, Löschen) werden mit Hashtabellen (hashtable, hashmap) implementiert. Hashmaps wurden 1953 von Hans Peter Luhn (IBM, USA; 01.07.1896-19.08.1964) entwickelt.
Um festzustellen, ob ein bestimmter Schlüssel (Zahl, Zeichenkette, ...) in der Hashmap enthalten ist oder nicht, ist eine Hashfunktion $h$ erforderlich: Sie liefert für jeden Schlüssel eine (natürliche) Zahl, z.B. $h($"Sabine Leutheusser-Schnarrenberger"$)=27535$. Diese Zahl entspricht dem Index der Feldkomponente, die den Zeiger auf den zugehörigen Datensatz mit dem jeweiligen Wert, z.B. "ist wahlberechtigt" bzw. "hat schon gewählt", enthält.
Ein anderes sehr praxisrelevantes Beispiel für Hashing ist die Abbildung von Webadressen (key) auf IP-Adressen (value), wie z.B. > h(google.com)=123456 und > IP-Array[123456]=216.58.208.46 (> ping google.com). Man nennt diesen Vorgang IP-Adressauflösung.
Dictionary Operationen
Ein Dictionary ist ein Abstrakter Datentyp (ADT), der in der Informatik sehr wichtig ist und sehr häufig zum Einsatz kommt. Er ist in allen gängigen Programmiersprachen implementiert. Es gibt drei wesentliche Operationen, nämlich insert, get und remove. (Stillschweigend setzt man die Existenz einer Initialisierungsoperation voraus.)
get(key):
Diese Operation gibt den vom angegebenen Schlüssel adressierten Wert zurück. Befindet sich kein Eintrag mit diesem Schlüssel im Dictionary, so wird null zurückgegeben.
Schlüssel und Werte können von beliebigem Datentyp sein. Konzeptionell reicht es aus, wenn man an natürliche Zahlen denkt, denn man kann jeden Datentyp in eine Zeichenkette serialisieren und anschließend auf eine natürliche Zahl abbilden (Gödelisierung), s. pre-hashing weiter unten.
insert(key, value):
Die Insert-Operation fügt ein Paar aus einem Schlüssel und einem Wert in die Datenstruktur ein.
remove(key):
Diese Operation entfernt einen (vorhandenen) Eintrag mit dem gegebenen Schlüssel aus dem Dictionary.
Die genannten drei Operationen ließen sich mit balancierten Bäumen, beispielsweise mit AVL-Bäumen, implementieren. Jedoch liegt die Laufzeit für diese Operationen bei einem balancierten Baum in $\mathcal{O}(\log n)$. Ein Ziel dieses Kapitels ist es, eine Datenstruktur zu implementieren, die dies in konstanter Zeit schafft. Da Dictionarys auch in Python (als > dict) implementiert sind, können wir am Ende unsere Implementierung mit der eingebauten Datenstruktur experimentell vergleichen.
Hashverfahren sind dann besonders effizient, wenn nach vielen anfänglichen Einfügeoperationen fast nur noch gesucht und fast nicht entfernt wird.
Wir ahnen schon, dass die Entwicklung einer geeigneten Hashfunktion eine besondere Herausforderung darstellt.
Hashfunktion
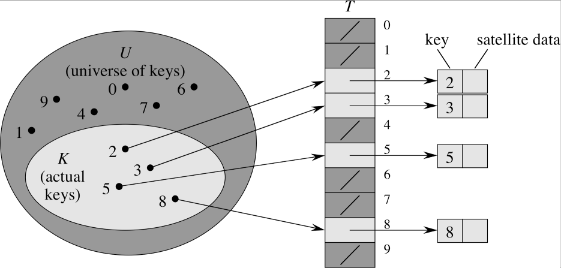
Von einer Hashfunktion $h:U\mapsto \{0,1,2,\ldots,m-1\}$, s. Abb. 1 für $m=10$, erwarten wir, dass sie folgende Eigenschaften erfüllt:
1. Im Allgemeinen sollen Schlüssel beliebigen Datentyps verwendet werden können.
2. Die $\left| K \right|=n$ zum Betrachtungszeitpunkt tatsächlich verwendeten Schlüssel, d.h. die Elemente der Schlüsselmenge $K\subset U$ sollen möglichst zufällig und gleichmäßig über die Indizes $\{0,1,2,\ldots,m-1\}$ des Feldes $T$ (in Abb. 1) mit $m \ll \left| U \right|$ gestreut werden. ($K$ ist im Allgemeinen nicht von vorn herein bekannt.) $U$ nennt man das Schlüsseluniversum, d.h. die Menge aller möglichen Schlüssel, s. Abb. 1. Für jeden (auch unbenutzten) Schlüssel wird Speicher insgesamt in $\mathcal{O}(\left| U \right|)$ reserviert und gegebenfalls verschwendet.
3. $h$ soll möglichst "einfach" und "schnell" berechenbar sein.
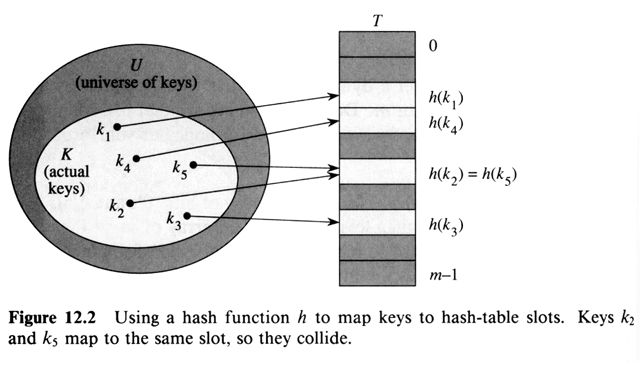
Die naheliegende Hoffnung, dass $h$ injektiv ist, d.h. dass zwei verschiedene, tatsächlich verwendete Schlüssel $s_1, s_2\in K$ mit $s_1\neq s_2$ unterschiedliche Hashwerte $h(s_1)\neq h(s_2)$ haben, kann im Allgemeinen nicht aufrecht erhalten werden. (In Abb. 1 ist das jedoch der Fall.) Selbst bei kleinen Schlüsselmengen im Vergleich zu der Hashtabellengröße ($m<n$) kann es zu Kollisionen kommen, selbst wenn andere Feldkomponenten noch frei sind. Von einer Kollision spricht man, wenn für zwei verschiedene Schlüssel die zugehörigen Hashwerte übereinstimmen. Welchen Zeiger sollte man dann eintragen? Die Kollisionsbehandlung wird weiter unten thematisiert.
Eine Hashfunktion ist idealerweise surjektiv, damit alle Indizes vorkommen können. Wir betrachten zwei klassische Methoden zur Konstruktion einer Hashfunktion $h$ mit den o.g. Eigenschaften, die vom Schlüsseluniversum $U$ auf $\{0, 1, \dotsc, m-1 \}$ abbildet.
DivisionsRest-Methode
$$ h(k) = k \bmod m $$
Diese Hashfunktion ist sehr einfach, jedoch nicht sonderlich gut. Ist $m$ eine Zweierpotenz, was bei Table Doubling (dynamische, bedarfsgerechte Verdopplung der Feldgröße; s.u.) immer der Fall ist, so teilt es sich unter Umständen sehr viele Teiler mit dem Schlüssel, was dazu führt, dass bestimmte Hash-Werte in der Menge $\{0, 1, \dotsc, m-1 \}$ besonders häufig vorkommen. Dies würde zu vielen Kollisionen führen, was die Datenstruktur ineffizient macht.
Die Empfehlung lautet, für $m$ eine Primzahl zu verwenden.
Multiplikationsmethode
Variante 1: $$ h(k) = \left\lfloor m\cdot ((\alpha \cdot k) \bmod 1) \right\rfloor $$
$x\bmod 1$ bedeutet, dass die Vorkommastellen von $x$ abgeschnitten werden. $\alpha$ ist eine reelle Zahl zwischen $0$ und $1$. Empfohlen wird $\alpha=\frac{\sqrt{5}-1}{2}= 0.618\ldots$. $m$ steht für die Hashtable-Größe.
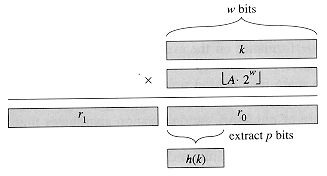
Variante 2: $$ h(k) = \left\lfloor \frac{m\cdot ((A \cdot k) \bmod 2^w)}{2^{w-r}} \right\rfloor $$
Diese Hashfunktion multipliziert den Schlüssel mit einem Faktor $A$. $w$ ist die Wortbreite des Systems. $A$ ist aus der Menge $\{0, 1, \dotsc , 2^{w-1} \}$ zu wählen. Das Ergebnis der Multiplikation $A \cdot k$ besteht aus $2w$ Bits. Anschließend wird $\bmod 2^w$ gebildet, was dazu führt, dass nur die rechten Hälfte, also die rechten $w$ Bits weiter betrachtet werden. Danach wird durch $2^{w-r}$ geteilt, was einem Bitshift von $w-r$ Bits entspricht. Als Ergebnis bleibt ein Wert mit $r$ Bits übrig. $r$ ist dabei so zu wählen, dass gilt $m=2^r$.
Diese Hashfunktion ist besser, da hier ein Durchmischen stattfindet und somit die Hashwerte besser, also gleichmäßiger, verteilt sind.
Implementation und pre-hashing
Bei dem folgenden Implementierungsversuch weist man, wie bei einem Array, der Datenstruktur einen festen Bereich im Speicher zu. Dann kann man direkt über den Index auf jeden Slot (Feldelement) zugreifen. Sind die Schlüssel natürliche Zahlen, so kann man - wie für die folgende Implementierung - festlegen, dass die Indices der Slots mit dem jeweils identischen Schlüssel übereinstimmen, d.h. die Hashfunktion ist $h:\mathbb{N}\mapsto\mathbb{N}$ mit $h(n)=n$. Die hier für $h$ verwendete identische Funktion gilt natürlich nur in diesem speziellen Fall, da die Schlüssel natürliche Zahlen sind, s. Abb. 1, und $m$ entsprechend groß gewählt werden kann.
Ein Dictionary (ADT) wird am besten mit einer hashtable implementiert.
Damit auch nicht natürlich-zahlige Schlüssel, z.B. Zeichenketten, verwendet werden können, wird eine sogenannte pre-hash-Funktion benötigt. Diese ist eine Funktion, die vom Schlüsseluniversum auf eine natürliche Zahl abbildet. In Python steht > hash() zur Verfügung.
Theoretisch betrachtet ist dies immer möglich, da alles, was in einem Computer dargestellt wird, diskret und endlich ist. Schließlich könnte man die Bits, durch welche das entsprechende Datum dargestellt wird, als nicht-negativen Integer auffassen und diesen als den pre-hash-Wert verwenden. Dies würde jedoch mitunter zu sehr großen Zahlen führen, weshalb man in der Praxis meist bessere pre-hash-Funktionen verwendet. Hat man beispielsweise eine Zeichenkette mit Zeichen aus a-z, so könnte man diese Zeichenkette als Zahl im Stellenwertsystem mit der Basis $26$ auffassen. (Derartige Abbildungen von Zeichenketten auf natürliche Zahlen spielen in der Berechenbarkeitstheorie unter dem Stichwort "Gödelisierung" eine wichtige Rolle.)
Beispiel:
$h($"adf"$) = 0 \cdot 26^2 + 3 \cdot 26 + 5 \cdot 1 = 83$
Nun kann man mit dem "geprehashten" Wert, der eine natürliche Zahl ist, so umgehen, als wäre dieser der eigentliche Schlüssel.
In der Programmiersprache Java beispielsweise findet dieses Pre-Hashing durch die > hashCode()-Methode, die jede Klasse implementiert, statt.
Kollisionen
Da $h$ wegen $m \ll \left| U \right|$ im Allgemeinen nicht injektiv ist, kann es zu Kollisionen kommen. Eine Kollision unter der Hashfunktion $h$ tritt auf, wenn für $k_i, k_j \in K$ mit $k_i \neq k_j$ gilt $h(k_i) = h(k_j)$, d.h. wenn zwei oder mehrere unterschiedliche Schlüssel den gleichen Hash-Wert haben.
Dies hat zur Folge, dass sie sich den gleichen Slot in der Hash Map teilen müssten. Um dieses Problem zu behandeln, gibt es mehrere Verfahren. Im Folgenden werden Hashing with Chaining und Open Addressing vorgestellt.
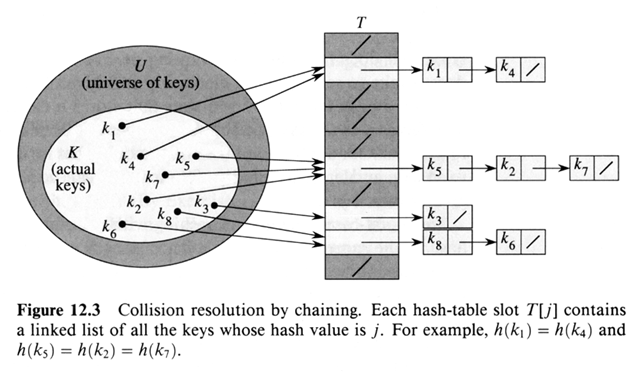
Hashing with chaining
Bei Hashing mit Verkettung der Überläufer wird in einem Slot der hashtable anstatt eines Wertes eine Linked List von Schlüssel-Wert-Paaren gespeichert. Kommt es beim Einfügen (Operation > insert) zu einer Kollision, so fügt man das Schlüssel-Wert-Paar ans Ende dieser Liste ein. Möchte man nach einem Schlüssel suchen (Operation > get), so muss man für den berechneten Slot durch die dort hinterlegte Liste iterieren.
Für die Implementation nutzen wir die SinglyLinkedList, die bereits in Kapitel 3 implementiert wurde. Der Einfachkeit halber, wird auf die Implementation der remove-Operation verzichtet.
Handelt es sich um eine sehr schlechte Hashfunktion, bei der es viele Kollisionen gibt, so kann es im Extrem passieren, dass (fast) alle Schlüssel den gleichen Hash-Wert haben und somit genau eine Linked List der Länge $n$ bilden. $n$ ist dabei die Anzahl der Elemente in der Datenstruktur, $n = \left| K \right|$. Die worst-case Komplexität liegt somit für alle Operationen in $\mathcal{O}(n)$. Für gute Hashfunktionen tritt dieser worst-case jedoch mit einer sehr geringen Wahrscheinlichkeit ein. Man kann $\mathcal{O}(\log n)$ im worst-case erreichen, indem man statt Linked Lists ballancierte Bäume verwendet.
Offene Hashverfahren
Open Addressing verwendet eine konzeptionell andere Variante zur "Kollisionsbehandlung". Dabei gibt es keine Verkettung, sondern es wird immer maximal ein Element in einem Slot gespeichert. Zwangsläufig muss $m \geqslant n$ gelten, d.h. die Anzahl der zu speichernden Elemente ist höchstens so groß wie die Hashtable-Größe.
Insert
Möchte man ein Element einfügen, dessen Schlüssel einen Hash-Wert hat, welcher einem bereits belegten Slot entspricht, so berechnet man einen neuen Hash und fügt das Element an dieser Stelle ein, falls dieser Slot frei ist. Die Hashfunktion bei Open Addressing ist also eine spezielle Hashfunktion, die nicht nur den Schlüssel als Parameter nimmt, sondern auch die Zahl des Versuches, um den es sich handelt. Die Hashfunktion $h$ ist also von der Form
$$ h: U \times \{0, 1, \dotsc, m-1\} \to \{0, 1, \dotsc, m-1\}. $$
Eine entscheidende Anforderung an solch eine Hashfunktion ist, dass der Vektor
$$ \begin{pmatrix}h(k, 0) & h(k, 1) & \cdots & h(k, m-1) \end{pmatrix} $$
mit $k\in U$ eine Permutation des Vektors
$$ \begin{pmatrix}0 & 1 & \cdots & m-1 \end{pmatrix} $$
ist.
Dies bedeutet, dass man nach $m$ Versuchen jeden der $m$ Slots genau einmal "durchprobiert" hat. Unter der Bedingung $m \geqslant n$, findet man demnach in jedem Fall einen freien Slot.
Search
Um einen Schlüssel zu suchen, wendet man die Hashfunktion $h$ ebenfalls mit entsprechendem Versuchszähler an. Man beginnt mit der Versuchszahl 0. Hat man Glück und findet den Schlüssel an dem entsprechenden Slot, so kann man aufhören und hat das Element gefunden. Handelt es sich um einen null Wert, so kann man auch aufhören, mit der Erkenntnis, dass sich der gesuchte Schlüssel nicht in der Hashmap befindet. Findet man an dem entsprechenden Slot, einen anderen Schlüssel, so muss man einen neuen Hash-Wert mit inkrementiertem Versuchszähler berechnen.
Dass man bei einem null Wert aufhören kann, liegt daran, dass wenn der gesuchte Schlüssel sich in der Datenstruktur befände, man ihn genau an dieser Stelle eingefügt hätte. Da er sich aber nicht dort befindet, befindet er sich auch nirgendswo anders in der Hashmap.
Remove
Das Entfernen von Schlüsseln aus einer Hashtable mit Open Addressing stellt sich etwas problematisch dar. Entfernt man nämlich ein Element, so funktioniert die Suche nicht mehr, da die Probiersequenz, die zum eigentlichen Schlüssel führen soll, nun durch ein gelöschtes Element unterbrochen wurde und der Suchalgorithmus "denken" würde, der Schlüssel befindet sich nicht in der Hashtable. Aus diesem Grund darf man das Element nicht einfach entfernen, sondern man muss einen deleted-Marker einführen, der signalisiert, dass man weitersuchen muss, da sich hier einmal ein Schlüssel befand. Der Suchalgorithmus bleibt prinzipiell der gleiche. Trifft man auf einen null-Wert, so kann man aufhören. Hat man den gesuchten Schlüssel gefunden, so kann man ebenfalls aufhören. Bei jedem anderen Wert - deleted-Marker eingeschlossen - muss man mit inkrementiertem Versuchszähler weiterprobieren.
Nun stellt sich die Frage, wie man eine Hashfunktion entwickelt, die den Anforderungen von Open Addressing entspricht. Sie muss zusätzlich eine Versuchszahl als Parameter nehmen und alle $m$ Slots genau einmal zurückgeben.
Linear Probing
Die naheliegendste Variante (lineares Sondieren) ist es, einfach beim nächsten Versuch um $i$ Slot(s) weiterzugehen, um auf einen freien Platz zum Schlüsseleintrag zu treffen. Also entwirft man folgende Hashfunktion, wobei $h'$ eine gewöhnliche einstellige Hashfunktion vom Typ $h':U \mapsto \{0, 1, \dotsc, m-1\}$ ist:
$$ h(k, i) = (h'(k) + i)\bmod m $$
Diese Hashfunktion ist einfach, aber leider schlecht. Hat sich etwa ein Cluster in der Hash Map gebildet, d.h. ein Zustand, bei dem viele Slots unmittelbar hintereinander belegt sind, so muss man definitiv das komplette Cluster durchiterieren, bis man einen freien Platz findet. Zudem hat man jetzt dieses Cluster auch noch um 1 vergrößert. Je größer ein Cluster ist, desto größer ist auch die Wahrscheinlichkeit es beim ersten Versuch zu treffen. Genau genommen $\frac{k}{m}$, wenn $k$ die Größe des Clusters ist und $m$ die Anzahl der Slots in der Hashmap.
Neben dem linearen Sondieren gibt es weitere verwandte Verfahren, die wir hier jedoch nicht näher betrachten:
- Quadratisches Sondieren
- Uniformes und zufälliges Sondieren
Double Hashing
Double Hashing verwendet zwei zufällig ausgewählte Hashfunktionen $h_1$ und $h_2$. Die Hashfunktion $h$ wird folgendermaßen definiert:
$$ h(k, i) = \left( h_1(k) + i h_2(k) \right) \bmod m $$
Damit sichergestellt ist, dass die Hashfunktion die erforderliche Permutation erzeugt, müssen alle Werte von $h_2(k)$ und $m$ relativ prim, also teilerfremd, sein.
Diese Hashfunktion erzeugt eine wesentlich durchmischtere Verteilung der Hash-Werte, wodurch sich (wahrscheinlich) keine Cluster bilden und diese somit besser geeignet ist.
Universelles Hashing
Hashing hat eine sehr gute average-case Komplexität von $\mathcal{O}(1)$ aber eine schlechte worst-case Effizienz in $\mathcal{O}(n)$. Die Idee des universellen Hashings besteht darin, aus einer sorgfältig ausgewählten Klasse von Hashfunktionen eine Hashfunktion zufällig auszuwählen.
Eine Möglichkeit für universelles Hashing ist die Klasse folgender Hashfunktionen:
$$ h(k) = ((a \cdot k + b) \bmod p) \bmod m $$
$p$ ist dabei eine Primzahl, für die gilt $p \geqslant m$. Wird eine Hashfunktion benötigt, so werden $a$ und $b$ zufällig aus der Menge $\{0, 1, \dotsc, p-1\}$ gewählt. Damit die Hash-Werte uniform auf $\{0, 1, \dotsc, m-1\}$ verteilt werden, müssen $p$ und $m$ teilerfremd sein. Durch die Bedingung, dass $p$ eine Primzahl ist, ist dies gegeben.
Da $a$ und $b$ zufällig gewählt werden, handelt es sich hierbei um eine Menge bzw. Klasse $\mathcal{H}$ von Hashfunktionen, die aus $p^2$ Funktionen besteht. Die hier vorgestellte Klasse von Hashfunktionen ist $\approx 1$-universell.
Eine Klasse $\mathcal{H}$ von Hashfunktionen ist $c$-universell, wenn für alle $x, y \in U$ mit $x \neq y$ mit zufällig ausgewählten $h \in \mathcal{H}$ gilt, dass $Pr(h(x) = h(y)) \leqslant c \cdot \frac{1}{m}$.
Ist die Klasse $\mathcal{H}$ 1-universell, so ist bei zufällig ausgewähltem $h$ die Wahrscheinlichkeit einer Kollision $\leqslant \frac{1}{m}$. Anders fomulliert gibt es nicht mehr als $c \cdot \frac{\left| \mathcal{H} \right|}{m}$ Hashfunktionen, die für ein Schlüsselpaar den gleichen Hash-Wert liefern.
Auf den Beweis, dass die genannte Klasse von Hashfunktionen universell ist, wird verzichtet.
Simple Uniform Hashing
Man spricht von Simple Uniform Hashing, wenn die Hashfunktion $h$ die Schlüsselmenge $K$ uniform zufällig auf die Werte $\{0, 1, \dotsc, m-1\}$ verteilt. Uniform zufällig bedeutet, dass jeder Hash-Wert gleich wahrscheinlich auftreten kann, so als ob man den Hash-Wert in einem Zufallsexperiment bestimmt.
Die Annahme, dass die Verteilung der Hash-Werte uniform ist, tritt in der Praxis nicht ein, jedoch hilft diese Annahme um zu verstehen, warum Operationen in einer Hashtable eine erwartete Laufzeit von $\mathcal{O}(1)$ haben:
Der Erwartungswert für die Anzahl der Elemente in einem Slot unter der Annahme von Uniform Hashing ist $n \cdot \frac{1}{m} = \frac{n}{m}$. Nehmen wir an, dass $n \in \mathcal{O}(m)$, also die Anzahl der Elemente $n$ maximal ein Vielfaches (Konstante als Faktor) von der Anzahl der Slots $m$ ist, so befinden sich voraussichtlich $\leqslant \frac{c \cdot m}{m} = c$ Elemente in einer Liste. Da $c$ eine Konstante ist, befinden sich lediglich $\mathcal{O}(1)$ Elemente in einer Liste.
Table Doubling
Das Problem ist, dass $n$ nicht vorhersagbar ist; schließlich können ständig Werte in das Dictionary eingefügt und daraus entfernt werden. Ist $n$ nämlich viel größer als $m$, so sind die Listen, durch die iteriert werden muss, sehr lang und somit wäre die Datenstruktur ineffizient. Wie kann man also sicherstellen, dass $n \in \mathcal{O}(m)$ immer gilt? Hierfür wird eine Technik angewandt, die bereits von dynamischen Arrays bekannt ist, nämlich das Verdoppeln der Größe, sobald die Anzahl der Elemente zu groß wird. Man spricht hier von Table Doubling.
Table Doubling wird durchgeführt, sobald $n > m$. Dabei wird die Anzahl der Slots $m$ verdoppelt. Die Anzahl der Slots beträgt anschließend $m'=2m$. Um die Elemente nun auf $m'$ Slots zu verteilen, ist eine neue Hashfunktion nötig. Handelt es sich zunächst beispielsweise um die sehr einfache Hashfunktion $h: x \mapsto x \bmod m$, so wird sie entsprechend zu $h': x \mapsto x \bmod m'$ abgeändert. Die bereits enthaltenen Elemente werden nun nach der neuen Hashfunktion $h'$ neu eingefügt, man spricht hier von Rehashing. Die Kosten für die ganze Table Doubling Operation betragen $\mathcal{O}(n)$. Analog wie für dynamische Arrays kann man aber zeigen, dass die Kosten amortisiert weiterhin lediglich $\mathcal{O}(1)$ betragen.
Durch Table Doubling ist sichergestellt, dass $n \in \mathcal{O}(m)$ immer gilt und somit die erwartete Laufzeit mit Uniform Hashing $\mathcal{O}(1)$ beträgt.
String Matching
In einem Text (große Datei, Zeichenkette/Wort über einem Alphabet) soll ein gegebener Substring gesucht, bzw. festgestellt werden, ob dieser überhaupt vorkommt. Natürlich kann die gesuchte Zeichenkette mehrfach im Text vorkommen. Wir beschränken uns hier auf die erste Fundstelle.
Dieses String-Matching-Problem tritt in der Praxis sehr häufig auf, beispielsweise in Texteditoren bei der Suche mit CTRL+F oder beim Linux Tool grep. Das Interesse an schnellen Suchverfahren ist offensichtlich und es sind auch recht viele entwickelt worden.
Ein naives Verfahren besteht darin, jede Position der Zeichenkette der Länge $n$ als potenzielle Startposition des gesuchten $k$-langen Substrings ($k\leq n$) anzusehen und dies durch Zeichenvergleich ($k$ Zeichen) zu überprüfen. Dieser Algorithmus hat einen Zeitaufwand in $\mathcal{O}((n-k+1)\cdot k)=\mathcal{O}(n\cdot k)$, d.h. einen linearen Zeitaufwand, wobei der konstante Faktor $k$ durchaus ins Gewicht fällt.
Rabin-Karp Algorithmus
Grundsätzlich folgt der 1987 bekannt gewordene String-Matching-Algorithmus von Rabin und Karp (beide Turing-Award-Preisträger) dem naiven Ansatz. Allerdings tritt an die Stelle des oben beschriebenen Zeichenvergleiches ein Vergleich der beiden zugehörigen Hashwerte. Da sich das gesuchte Muster nicht verändert, wird dessen Hashwert einmalig und vor Beginn der Suche berechnet. Gedanklich schiebt der Suchprozess das Muster wie ein Fenster zeichenweise nach rechts über den Text, berechnet den Hashwert des im Fenster erscheinenden Substrings und vergleicht diesen mit dem (unveränderten) Hashwert des Musters.
Stimmen die beiden jeweils betrachten Hashwerte (Muster und Textausschnitt) nicht überein, so weiß man, dass der gesuchte Substring nicht an dieser Position beginnt und die Suche geht weiter. Stimmen sie überein, kann es an einer Kollision der Hashfunktion liegen. Dann wird ein Treffer vorgegaukelt. In diesem Fall muss ein zeichenweiser Vergleich folgen, genau wie beim naiven Ansatz. Im (theoretisch) schlechtesten Fall gibt es in jedem Schritt eine Kollision. Dann stimmt das Verfahren mit dem naiven überein und arbeitet in $\mathcal{O}(n\cdot k)$. Es bleibt also bei einem linearen Aufwand im worst case.
Eine Effizienzverbesserung, statt $\mathcal{O}(n\cdot k)$ nun $\mathcal{O}(n+k)$ im average case, ergibt sich durch die vereinfachte Berechnung der Hashwerte für die Substrings durch sukzessive Adaption (rolling hash). Schiebt man nämlich das Fenster um ein Zeichen nach rechts, so erscheint ein Substring, der dem vorherigen sehr ähnlich ist: Das erste Zeichen wurde (am Anfang) entfernt und am Ende wurde das nächste Zeichen des Textes hinzu gefügt. $k-2$ Zeichen bleiben unverändert. Dies führt zu der Idee, den Hashwert der jeweils nächsten Zeichenkette aus dem Hashwert der vorher betrachteten Zeichenkette zu berechnen. Diese Berechnung kann mit konstantem Aufwand erfolgen, d.h. in $\mathcal{O}(1)$ liegen, da nur genau zwei Zeichen einfließen, nicht etwa $n$.
Als Hashfunktion könnte man nun beispielsweise die Summe der Zeichencodes der betrachteten Zeichenkette verwenden. Dies würde jedoch zu zahlreichen Kollisionen führen, die sich, wie oben beschrieben, negativ auf die Effizienz des Verfahrens auswirken würden. Die von uns gewählte Hashfunktion mit Werten im $b$-adischen System bringt das Problem mit sich, dass die ggf. entstehenden großen Zahlen, schon bei Alphabeten mit 256 Zeichen, nicht mir in den Datentyp gängiger Programmiersprachen passen und von daher nicht verarbeitet werden können. Deshalb setzt man gern die modulo-Operation ein, die man wegen der Kollisionsvermeidung üblicherweise auf eine Primzahl anwendet.
Konstruiert man die Hashfunktion so, dass man den String als Zahl mit der Basis $b$ auffasst, so kann man den Hashwert nach dem Entfernen des ersten Zeichens und Anfügen eines neuen Zeichens, mit Hilfe von einfachen Operationen in konstanter Zeit berechnen. In folgendem Beispiel wählen wir das Alphabet $A=\{0, 1, 2,\ldots,25\}$ mit der Größe $|A|=26=b$.
Angenommen das Fenster steht an der Position, an der der (nicht gesuchte) Substring $\verb|hash|$ mit einer Länge von $k=4$ beginnt. Dann ergibt sich
\[h(\verb|hash|) = 7 \cdot 26^3 + (0 \cdot 26^2 + 18 \cdot 26^1 + 7 \cdot 26^0) = (7,0,18,7)_{26}= 123507.\]
Unter der Annahme, dass der Text nach $\verb|hash|$ mit $\verb|x|$ weitergeht, berechnen wir
\[h(\verb|ashx|)=(0 \cdot 26^3 + 18 \cdot 26^2 + 7 \cdot 26^1) + 23 \cdot 26^0 = (0,18,7,23)_{26} = 12373\]
und nun viel besser aus $h(\verb|hash|)$:
\[h(\verb|ashx|)=(h(\verb|hash|) - \textbf{7}\cdot 26^3)\cdot 26 + \textbf{23} = (0,18,7,23)_{26} = 12373.\]
Dies können wir unter Verwendung von $(7,0,18,7,23) = (a_0, a_1,\ldots, a_k)$ und $T_{i}=\verb|ash|, T_{i+1}=\verb|ashx|$, mit $|T_{i+1}|=|T_{i}|=k$ verallgemeinern zu:
\[\textbf{h(T}_{\textbf{i+1}})=(\textbf{h(T}_{\textbf{i}}) - a_0\cdot b^{k-1})\cdot b + a_k = 12373.\]
Wenn wir die Überlegungen zu den gewünschten Eigenschaften der Hashfunktion (s.o.) noch hinzunehmen, erhalten wir
\[\textbf{h(T}_{\textbf{i+1}})=\left((\textbf{h(T}_{\textbf{i}}) - a_0\cdot b^{k-1})\cdot b + a_k\right)\bmod q, \text{ mit Primzahl }q.\]
Der Algorithmus iteriert nun durch $n-k+1$ Zeichen des Strings und vergleicht den Rolling Hashwert des Substrings ab dem entsprechenden Index mit dem Hashwert des gesuchten Substrings, der im Voraus berechnet wurde. Die Zeiteffizienz des Algorithmus beträgt im mittleren Fall $\mathcal{O}(n+k)$. Dieser Algorithmus ist im Vergleich zum naiven Brute-Force Ansatz besonders effizient, wenn $k$, also die Länge des gesuchten Substrings, groß ist.
Hashmaps zur Implementierung von Datenstrukturen
Im average case liegen die Kosten für Zugriff/Suche/Look-Up, Einfügen in die und Entfernen eines Elements aus der Hashmap in $\mathcal{O}(1)$, d.h. konstanter Zeitaufwand. Mit Datenstrukturen, die auf Anordnung von Elementen und Schlüsselvergleich beruhen, schafft man das bestenfalls mit $\mathcal{O}(\log n)$ (Binäre Suche). $\mathcal{O}(1)$ gilt allerdings nur für Hashmaps geeigneter Größe und Hash-Funktionen mit Kollisionsminimierung. Deshalb verschlechtert sich die Effizienz mit zunehmendem $n$. Von daher muss man im worst case mit $\mathcal{O}(n)$ rechnen.
Aufgrund dieser vergleichsweise günstigen Zeitkomplexität werden Hashmaps bei der Implementation diverser Datenstrukturen verwendet: Assoziatives Feld, dictionary, set, ... In Anwendungssoftware findet man Hashmaps in der Datenbank-Indizierung und bei Caches.
Trotzdem wird Binäre Suche eingesetzt, denn man kann damit eine breitere Problempalette bearbeiten, wie z.B. die Suche des nächstkleineren oder nächstgrößeren Elements in einem Array (bezogen auf ein Ziel), insbesondere wenn es nicht zum Feld gehört.
Allein die eingangs genannten Anwendungsfälle eröffnen Bereiche, in denen Hashing nahezu unverzichtbar ist. In erster Linie muss man natürlich eine Datenstruktur wählen, die die angestrebte Lösungsidee adäquat repräsentiert. Die Auswahl passender Datenstrukturen ist eine der wichtigsten Entscheidungen im Softwareentwicklungsprozess.