Bäume
Aus ProgrammingWiki
Mathematisch betrachtet ist die Menge der Bäume eine Teilmenge der Menge der ungerichteten Graphen.
Definition
Ein ungerichteter Graph $G = (V, E)$ ist ein Baum, wenn es für alle $u, v \in V$ genau einen Pfad von $u$ nach $v$ gibt.
In einem Baum gibt es also zu jedem Knotenpaar genau einen Pfad. Alternativ kann man sagen, dass ein ungerichteter Graph ein Baum ist, wenn er zusammenhängend ist und keine Zyklen enthält. Ein Graph ist zusammenhängend, wenn jeder Knoten von jedem anderen Knoten aus erreichbar ist.
Inhaltsverzeichnis |
Beispiele
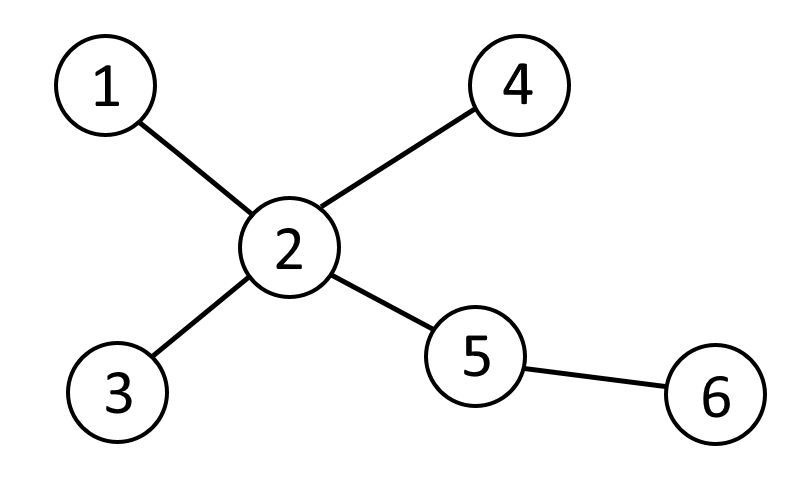
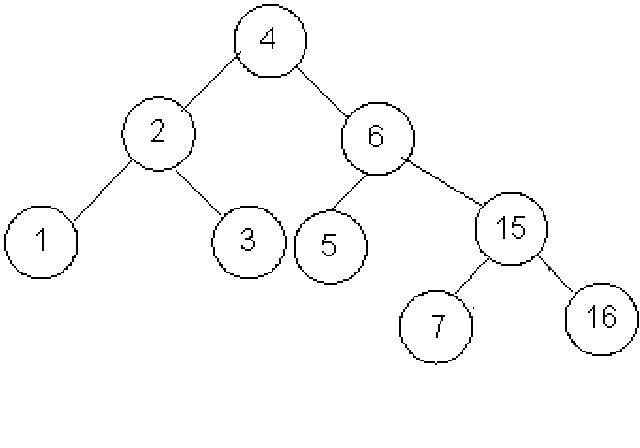
Der folgende Graph
ist ein Baum, da er keine Kreise enthält und zusammenhängend ist.
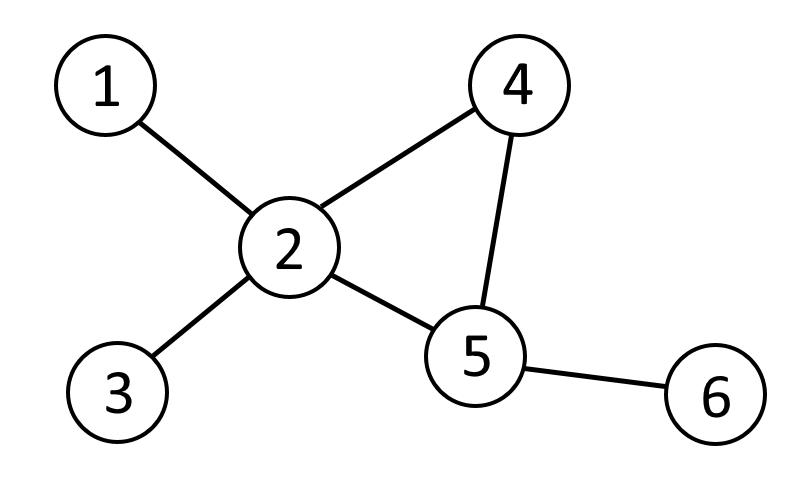
Der folgende Graph
ist kein Baum, da er einen Kreis $(2,4,5)$ enthält.
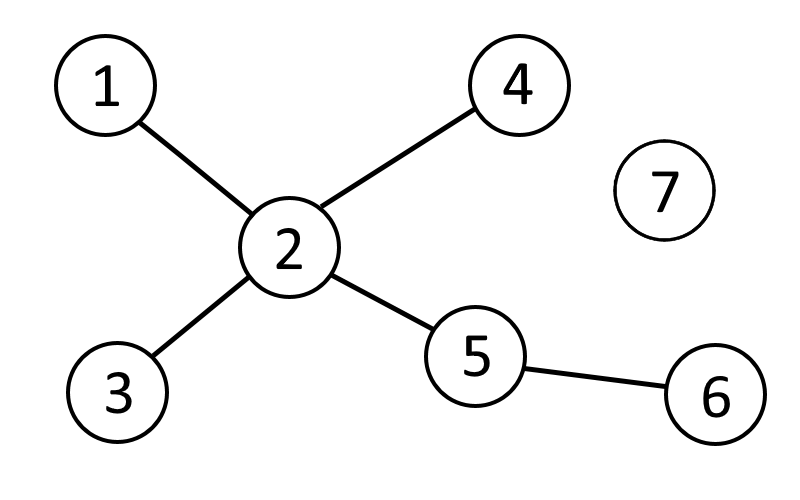
Der folgende Graph
ist kein Baum, da er nicht zusammenhängend ist: Knoten mit dem Wert $7$ ist nicht erreichbar.
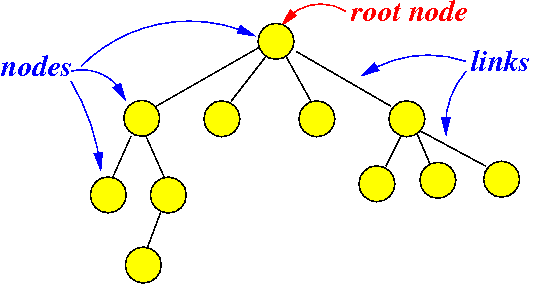
Bäume mit Wurzel (Wurzelbäume)
In der Informatik betrachtet man meistens Wurzelbäume (rooted trees).
Definition 6.1
Wurzelbäume sind gerichtete oder ungerichtete Bäume, bei denen genau ein Knoten Wurzel (root) ist. Von diesem Wurzelknoten sind alle anderen Knoten über genau einen Pfad (Folge von Knoten, die darin höchstens einmal vorkommen) erreichbar. Der Wurzelknoten ist der einzige Knoten des Graphen, der keinen Vorgänger besitzt.
Beispiel:
Binärbäume
Definition 6.2
Binärbäume (binary trees) sind Bäume mit Wurzel, bei denen jeder Knoten höchstens zwei direkte Nachkommen (Kindknoten) hat.
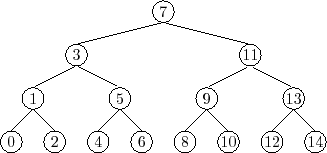
Beispiel: gerichteter Binärbaum
Dabei besteht ein Knoten (Node) aus genau einem Wert (allg. Schlüssel: key), einem linken und einem rechten Binärbaum mit folgender rekursiver Definition.
Ein Binärbaum $\ldots$
+ $\ldots$ ist entweder leer (null), + $\ldots$ oder besteht aus einem linken und einem rechten Binärbaum.
Es ist also möglich, dass genau ein Kind oder beide Kinder aus einem leeren Binärbaum besteht/en. Sind sowohl linkes als auch rechtes Kind null, so handelt es sich bei dem betrachteten Knoten um ein Blatt (leaf).
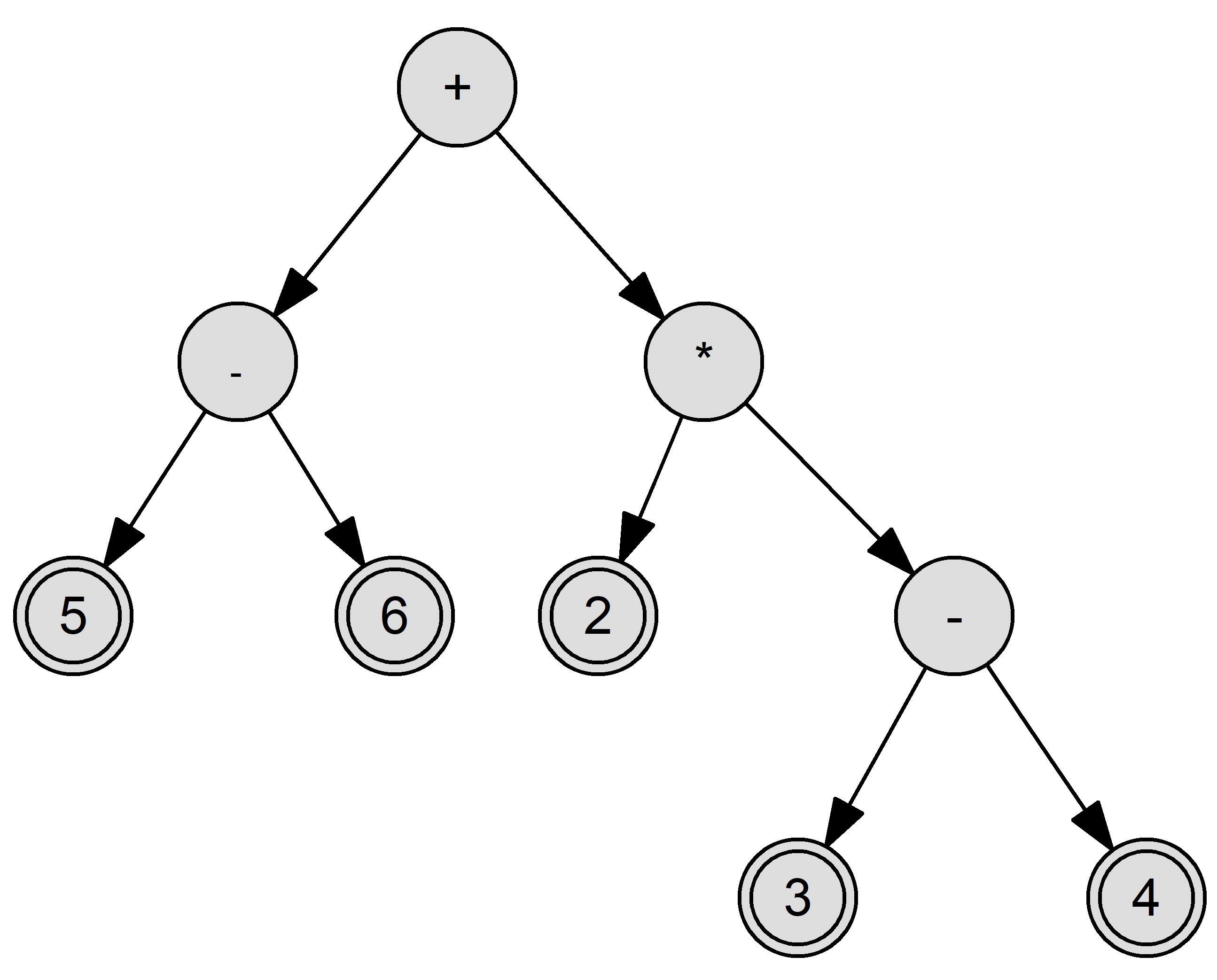
Für arithmetische Ausdrücke, die ausschließlich Binäroperationen enthalten, können Operatorbäume angegeben werden. Während die inneren Knoten den Operatoren vorbehalten sind, enthalten die Blätter die entsprechenden Operanden.
Beispiel: gerichteter Operatorbaum für den Ausdruck $(5-6)+(2\cdot(3-4))$
Definition 6.3
Manchmal wird für Binärbäume zusätzlich gefordert, dass sie vollständig sind. Dann müssen alle $k\geq 0$ Niveaus (Schichten) eines Binärbaums die jeweils maximale Knotenanzahl $2^k (k\geq 0)$ aufweisen und sämtliche Blätter dieselbe Tiefe haben.
Definition 6.4
Die Tiefe $t$ eines Knotens $(t\geq 0)$ ist sein Abstand zur Wurzel, d.h. die Anzahl der Kanten auf dem Pfad von diesem Knoten zum Wurzelknoten. Sämtliche Knoten mit Tiefe $t$ liegen auf Niveau $t$.
Definition 6.5
Die Höhe $h$ eines Baumes $(\geq 0)$ ist die maximale Tiefe aller Knoten.
Dies kann man für einen Baum mit Wurzelknoten $w$ rekursiv definieren:
$$h(w)=\begin{cases} 0, & \text{wenn } w\text{ ein Blatt ist.}\\ \max(h(w_1),h(w_2),\ldots,h(w_r))+1, & \text{für alle } r \text{ Kindknoten } w_1,w_2,\ldots,w_r\text{ von } w. \end{cases}$$
Implementation mit obigem Beispiel
Binäre Suchbäume
Ein Binärer Suchbaum (BST = binary search tree) ist eine Datenstruktur, die verwendet wird, wenn sowohl schnelles Einfügen, als auch schnelles Suchen eines Elements gefordert werden.
Wir betrachten zunächst Datenstrukturen, die bereits im Kapitel "Abstrakte Datentypen und Datenstrukturen" vorgestellt wurden, nämlich eine Linked List, ein unsortiertes und ein sortiertes Array. Dazu untersuchen wir die Worst-case-Aufwände der Insert- und der Search-Operation.
Bei einer Linked List findet das Einfügen in $\mathcal{O}(1)$ statt, da lediglich ein neues Element angelegt und entsprechend ein Pointer bearbeitet wird. Der zum Suchen eines Elements erforderliche Zeitaufwand liegt in $\mathcal{O}(n)$, da im worst case durch die komplette Liste gegangen werden muss, um das Element zu finden.
Bei einem unsortierten Array beträgt der Aufwand zum Einfügen $\mathcal{O}(n)$, da ein neues Array erstellt werden muss und alle Werte kopiert werden. Wie bei der Linked List muss durch alle Elemente iteriert werden, um ein bestimmtes Element zu finden. Dadurch ist auch hier der Aufwand zum Suchen $\mathcal{O}(n)$.
Bei einem sortierten Array kann Binary Search verwendet werden, um ein Element zu finden, dadurch beträgt der Aufwand hierfür lediglich $\mathcal{O}(\log n)$. Das Einfügen ist jedoch ineffizient. Man müsste zunächst die Stelle finden, wo das neue Element eingefügt werden soll, um die Sortierung beizubehalten. Dies nimmt $\mathcal{O}(\log n)$ in Anspruch. Anschließend muss man allerdings $\mathcal{O}(n)$ Elemente dahinter um eine Position nach hinten verschieben, bzw. in ein neues Array kopieren. Dadurch ergibt sich für die Insert-Operation ein Aufwand von $\mathcal{O}(n)$.
Definition
Ein Binärer Suchbaum ist ein Binärbaum, bei dem für alle Knoten gilt, dass jeder Knotenwert des linken Teilbaums kleiner als der Wert des Elternknotens ist und der Wert des Elternknotens kleiner als jeder Knotenwert des rechten Teilbaums ist.
Dies lässt sich nicht nur für Zahlen anwenden, sondern für alle Datentypen, für die eine Ordnungsrelation definiert ist. So gilt verallgemeinert, dass für jeden Knoten die Relation aus jedem Knotenwert des linken Subbaums und dem Wert des Elternknotens zur definierten Ordnungsrelation gehört, sowie alle Relationen aus dem Wert des Elternknoten und jedem Knotenwert des rechten Subbaums.
Beispiel
Search
Um einen Wert in einem BST (binary search tree) zu finden, wird ein Verfahren ähnlich wie Binary Search angewandt. Die Suche beginnt bei der Wurzel. Stimmt der gesuchte Wert mit dem der Wurzel überein, so hat man den Knoten gefunden. Ist der gesuchte Wert kleiner als der Wert der Wurzel, so wird die Suche rekursiv mit der Wurzel des linken Subbaums fortgesetzt, da sich hier alle Werte befinden, die kleiner als die Wurzel sind. Ist der gesuchte Wert größer, so wird rekursiv im rechten Subbaum weitergesucht. Der Algorithmus terminiert, sobald der gesuchte Wert gefunden (Knoten gefunden) oder ein Blatt mit anderem Wert (gesuchter Knoten nicht vorhanden) erreicht wurde.
Die Höhe des binären Suchbaums im obigen Beispiel beträgt 3.
Da bei der Suche im BST maximal $h$ (Höhe $h$ des Baums) Knoten besucht werden, beträgt der Zeitaufwand zur Suche $\mathcal{O}(h)$. Was dies in Bezug auf $n$ (der Anzahl der Elemente) bedeutet, wird weiter unten erläutert.
Insert
Wir gehen davon aus, dass sich keine Duplikate (Knoten mit dem gleichen Wert) im BST befinden.
Um ein Element einzufügen, muss zunächst die Suche im BST durchgeführt werden. Da sich das Element noch nicht im BST befindet, gelangt man an das Blatt, das dem einzufügenden Wert am nächsten ist. Hierfür benötigt man im worst case einen Aufwand von $\mathcal{O}(h)$. An dieser Stelle muss man nun einen neuen Knoten einfügen. Ist der einzufügende Wert größer, so wird er als rechtes Kind eingefügt, ist er kleiner, so wird er als linkes Kind eingefügt.
Remove
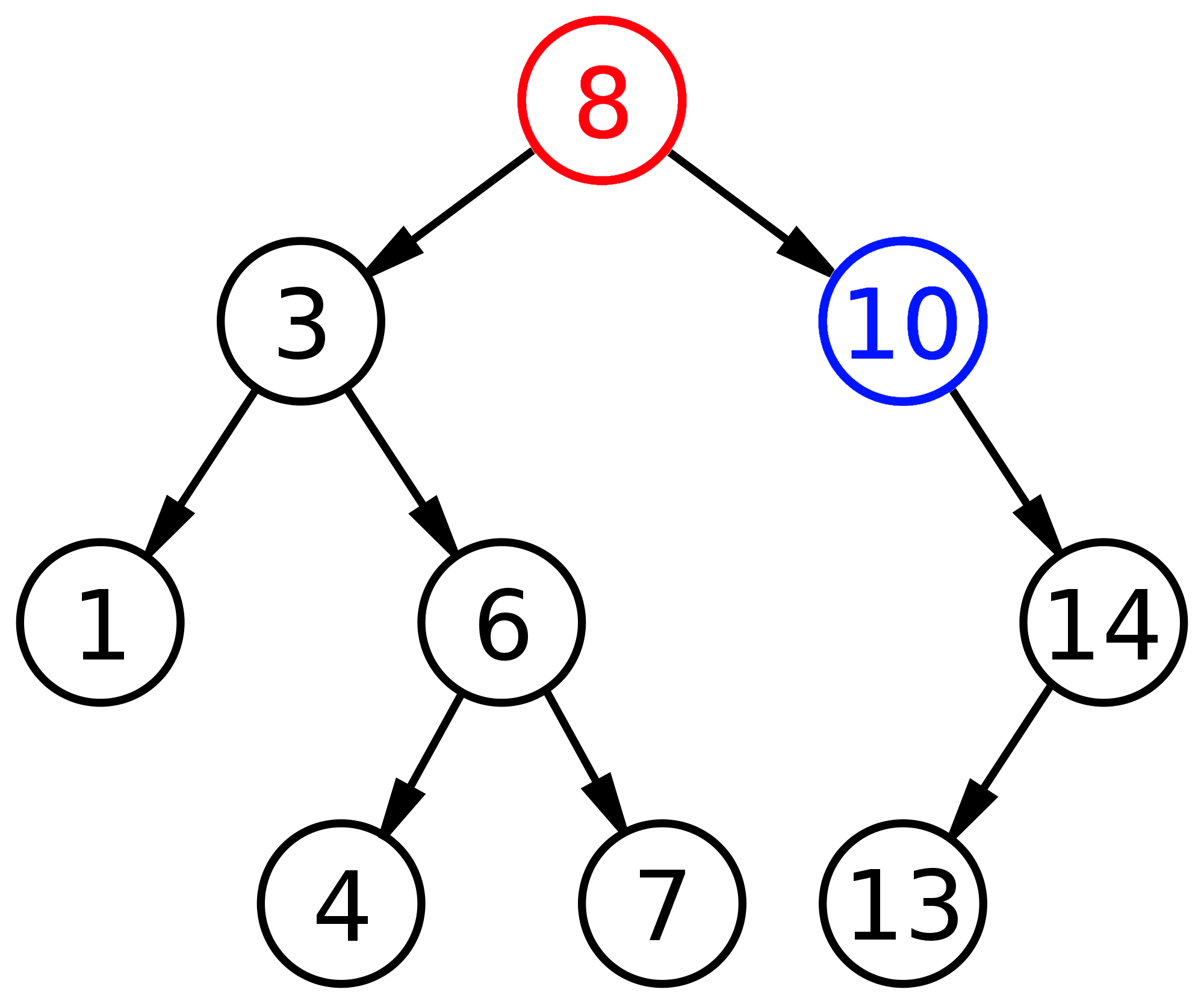
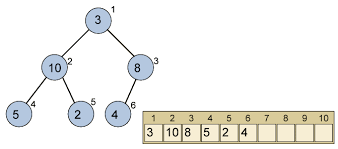
Um ein Element (rot, 4) zu entfernen, muss man es zuerst suchen. Dieser Vorgang wurde bereits beschrieben und ist mit einem Aufwand von $\mathcal{O}(h)$ machbar. Handelt es sich bei dem zu entfernenden Element um ein Blatt im Baum, d.h. der Knoten hat kein Kind, so kann dieses Element einfach entfernt werden, d.h. zugehörigen link auf NULL.
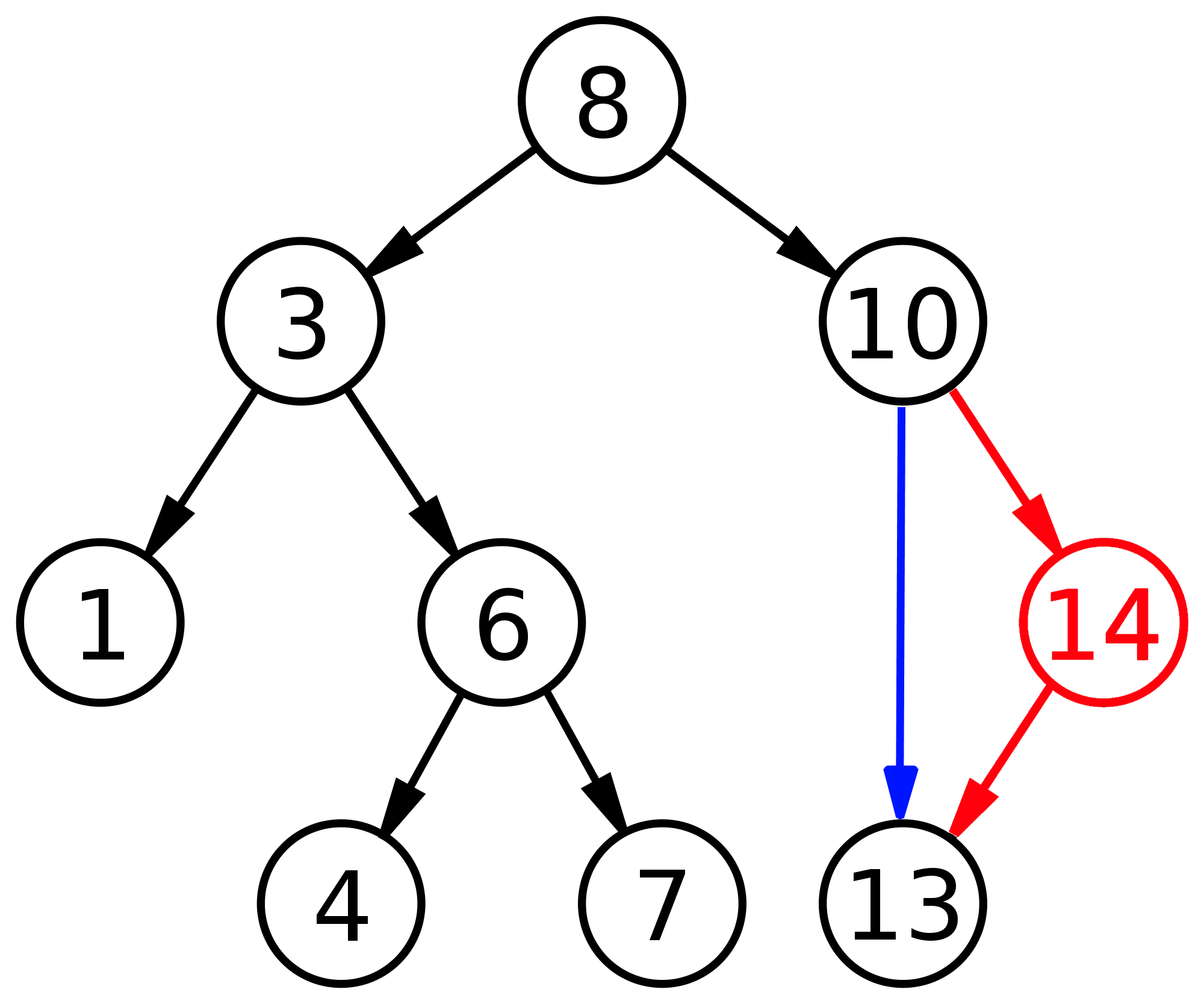
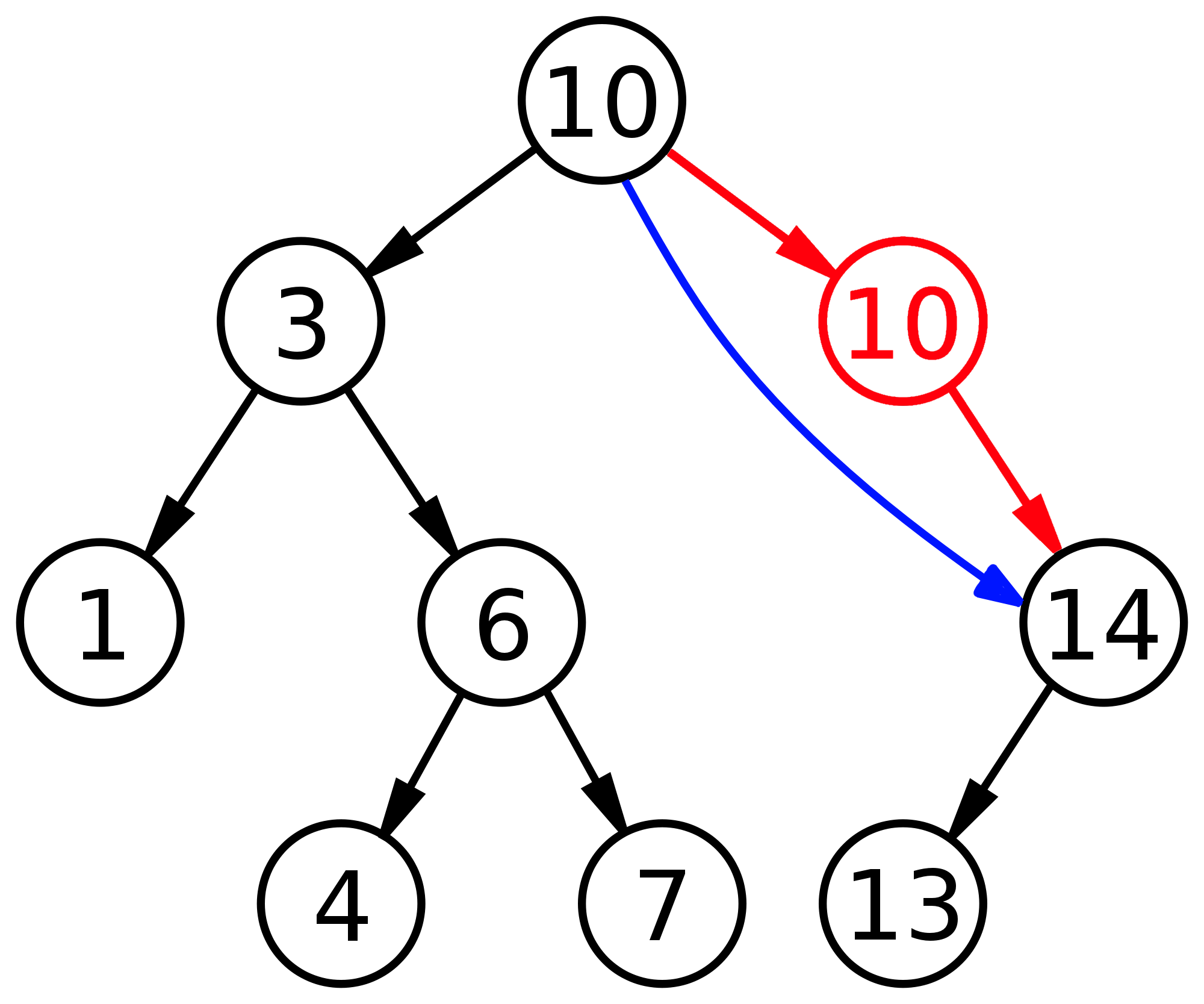
Handelt es sich bei dem zu löschenden Knoten (rot, 14) um einen inneren Knoten der genau ein (linkes oder rechtes) Kind besitzt, so wird dieser Knoten gelöscht und sein Sohn (schwarz, 13) wird der Sohn (blaue Kante) seines Vorgängers (schwarz, 10).
Hat der zu löschende Knoten (rot, 8) zwei Kinder, so muss die entstandene Lücke im Baum gefüllt werden. Dafür wird im rechten Teilbaum der kleinste Wert, d.h. der ganz links stehende, Knoten, also der mit dem kleinsten Wert (blau, 10) gesucht und dort eingesetzt, wo das zu löschende Element (rot, 8) entfernt wurde. Das zum Schließen der Lücke verwendete Element mit dem kleinsten Wert (blau, 10) wird anschließend aus dem rechten Teilbaum entfernt. Es ist sicher, dass hierfür einer der beiden obigen Fälle passt.
Alternativ kann man das größte Element des linken Subbaums nehmen. Um das größte Element zu finden, muss man entsprechend immer nach rechts im Baum gehen.
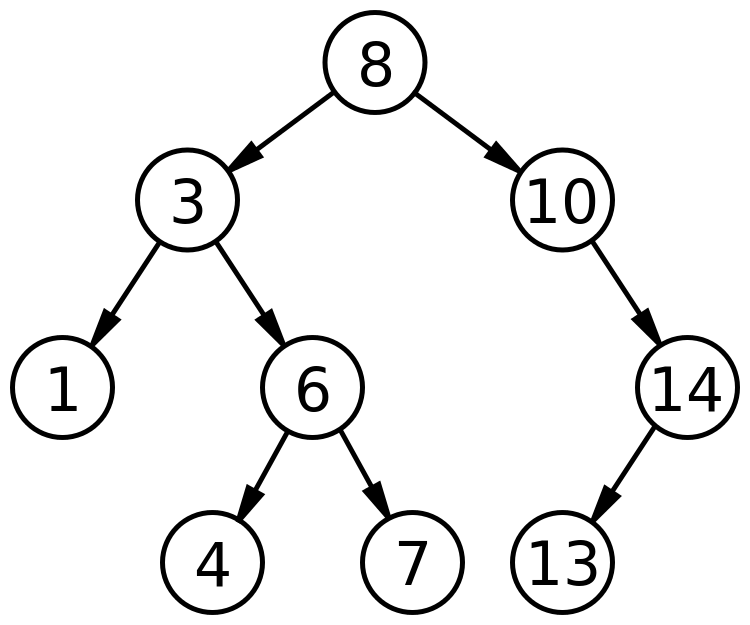
Oben wurden die Search- und Insert-Operationen eines BST mit dem folgenden Beispiel implementiert:
Testhalber geben wir einige Werte des BST aus. Sie stimmen mit den erwarteten Werten überein.
Für die Werte 1 und 10 konnten Knoten gefunden werden, für den Wert 2 nicht, da er sich nicht im BST befindet.
Mit der Remove-Operation soll der Wurzelknoten mit dem Wert 8 entfernt werden.
Tree Traversal (Baumdurchlauf)
Um einen Baum zu traversieren, benutzt man Depth-First-Search. Da es sich bei einem Binärbaum nicht um eine Liste von benachbarten Knoten handelt, sondern um zwei Pointer auf je einen Kindknoten, wird DFS hier nicht auf eine Liste, sondern auf die beiden Kinder rekursiv angewandt.
Fährt man mit dem Finger entlang der jeweiligen Kante zu einem Kindknoten, so ergeben sich drei Berührungen:
- Berührung direkt durch Eintreffen entlang der Kante
- Berührung nach dem "Abfahren" des linken Teilbaums
- Berührung nach dem "Abfahren" des rechten Teilbaums
Die Position der Druckanweisung bezogen auf die Folge der Knotenberührungen bestimmt, ob es sich um Pre-Order, In-Order oder Post-Order Traversal handelt.
Pre-Order Traversal
Bei Pre-Order Traversal wird direkt beim ersten Besuch des Knotens die gewünschte Aktion auf dem Knoten ausgeführt, in dem Fall das Ausgeben des Wertes des Knotens. Erst danach folgen die rekursiven Aufrufe auf den beiden Kindern.
In-Order Traversal
Bei In-Order Traversal findet zunächst der rekursive Aufruf auf dem linken Kind statt, danach die Aktion auf dem Knoten und anschließend der rekursive Aufruf auf dem rechten Kind. Dies hat zur Folge, dass die Aktion immer beim zweiten Besuch eines Knoten ausgeführt wird.
Führt man In-Order Traversal auf einem Binären Suchbaum aus, so werden die Werte in sortierter Reihenfolge ausgegeben.
Post-Order Traversal
Bei Post-Order Traversal finden zunächst die rekursiven Aufrufe statt und anschließend die Aktion auf dem Knoten. Dies hat zur Folge, dass die Aktion beim dritten Besuch eines Knoten stattfindet.
Für das Beispiel
ergeben sich folgende Reihenfolgen:
Höhe eines binären Suchbaums
Wir haben festgestellt, dass man in einem gewöhnlichen binären Suchbaum mit einem Zeitaufwand von $\mathcal{O}(h)$ ein Element finden kann, wobei $h$ die Höhe des Baums ist. Die Höhe eines Baums ist die Länge des Pfades (Anzahl der Kanten) zum am weitesten von ihm entfernten Blatt. Dies kann folgendermaßen rekursiv definiert werden:
Definition 6.6 $$ \text{height}(n) = \begin{cases} -1, & \text{wenn $n=$ null}. \\ \text{max}\{\text{height}(n.\text{left}), \text{height}(n.\text{right})\} + 1, & \text{sonst}. \end{cases} $$
Existiert der Knoten nicht, so ist die Höhe -1. Besteht der Baum aus genau einem Knoten, so hat der Weg zum Blatt $0$ die Länge $0$, also ist die Höhe $0$: $\max(-1,-1)+1=0$.
Es ist gut zu wissen, dass für die Suche eines Elements in einem binären Suchbaum $\mathcal{O}(h)$ gilt. Wir erwarten jedoch einen Ausdruck in $n$ für den asymptotischen Aufwand in Abhängigkeit von der Anzahl der Elemente $n$ im BST?
Im Idealfall haben wir es mit einem balancierten BST zu tun:
Ein BST ist balanciert, wenn bei jedem Knoten der linke Subbaum genauso viele Elemente enthält, wie der rechte Subbaum.
Hat der Baum die Höhe $h$, so besitzt er höchstens $n=2^0+2^1+2^2+\ldots+2^h=2^{h+1}-1$ Knoten/Elemente (endliche geometrische Reihe). Dann gilt $2^{h+1}-1=n,\ 2^h=\frac{n+1}{2},\ h=\log_2(n+1)-1$ und damit liegt $h$ in $\mathcal{O}(\log_2n)$. Ist der Binärbaum balanciert, so beträgt der Aufwand zum Suchen $\mathcal{O}(\log n)$. Dies ist genau unser Ziel.
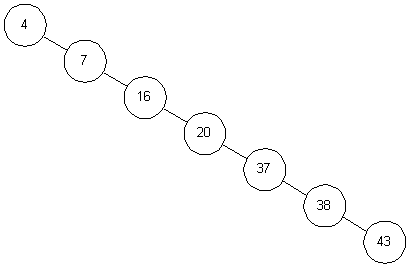
Jedoch sieht ein BST leider nicht immer so aus. Fügt man beispielsweise eine bereits sortierte Liste hintereinander in einen BST ein, so erhält man einen BST wie diesen:
Dies entspricht eher einer linearen Liste als einem Binärbaum. Es ist offensichtlich, dass hier der Aufwand zum Suchen linear in $n$ und nicht logarithmisch ist.
AVL-Bäume
Gesucht ist also ein Verfahren, mit welchem man sicherstellt, dass ein Binärer Suchbaum so balanciert wie möglich ist. Der historisch erste Vorschlag (1962) geht auf Adelson-Velskij und Landis zurück: AVL-Bäume.
Definition 6.7 Bei einem AVL-Baum gilt für jeden Knoten $n$ folgende Invariante (eine Größe/Relation, die bei Eintritt gewisser Veränderungen unveränderlich bleibt):
$$ \lvert \text{height}(n.\text{right}) - \text{height}(n.\text{left}) \rvert \leqslant 1 $$
Damit wird gesagt: Die Höhe des linken Subbaums unterscheidet sich maximal um 1 von der Höhe des rechten Subbaums.
Ideal wäre, wenn bei jedem Knoten der rechte Subbaum die gleiche Höhe hätte wie der linke Subbaum. Doch so ein perfekt balancierter Binärbaum ist nur möglich, wenn er $2^n - 1,\ n \in \mathbb{N}$, Knoten hat. Weiter unten zeigen wir, dass auch unter der Bedingung, dass sich die Höhen um nicht mehr als 1 unterscheiden, man trotzdem eine logarithmische Laufzeit erzielt.
Insert
Zunächst findet das Einfügen eines neuen Elements wie bei einem gewöhnlichen BST statt. Man sucht zunächst nach einem Knoten mit dem einzufügenden Wert, um es dann an passender Stelle einzufügen.
Bei einem gewöhnlichen BST wird jedoch nicht sichergestellt, dass die oben beschriebene Invariante nach dem Einfügen gilt. Bei einem AVL-Baum ist also nach dem Einfügen eine Operation anzuwenden, die genau das gewährleistet.
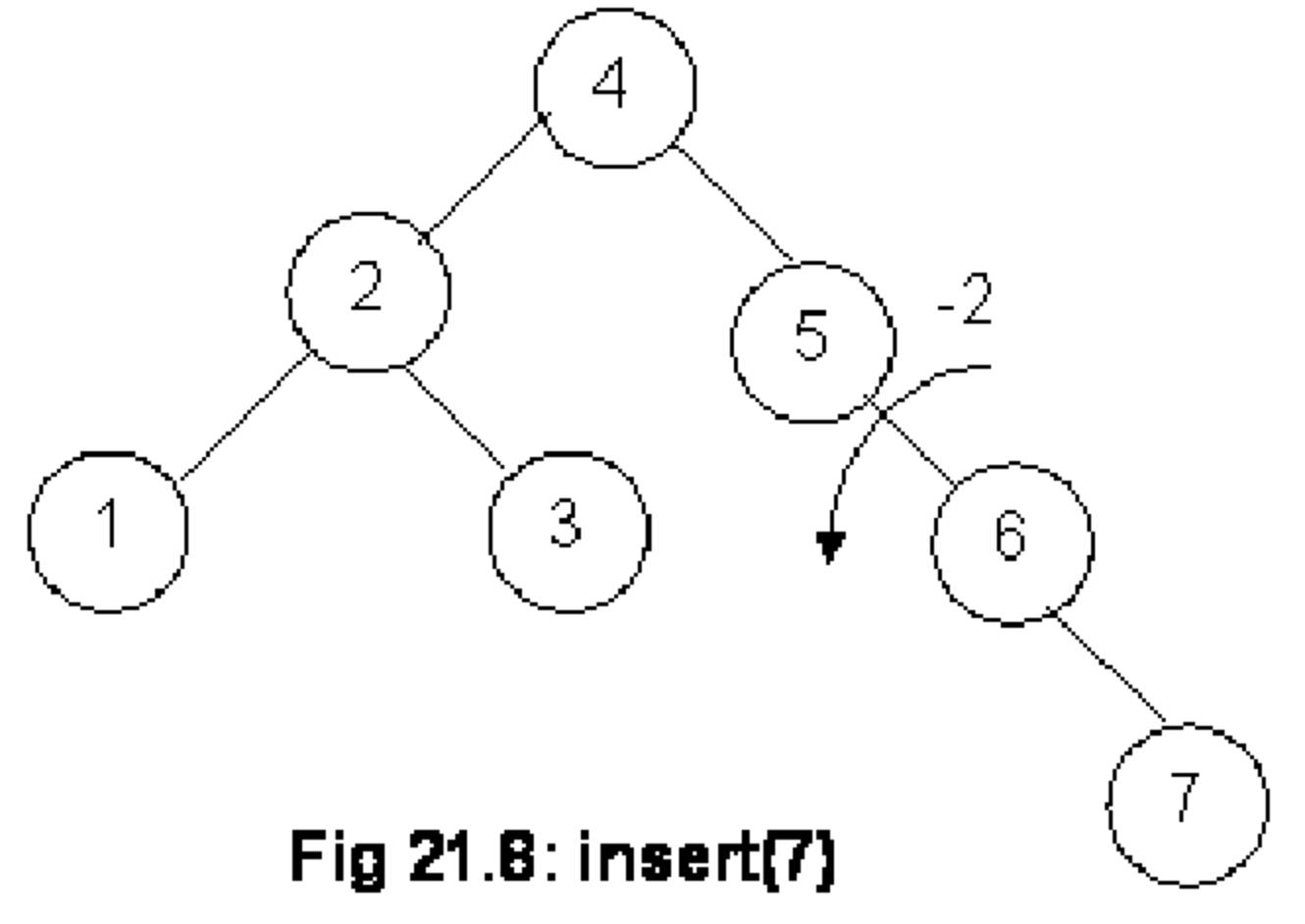
Betrachten wir das Beispiel:
Hier ist die Invariante des AVL-Baums verletzt, da für den Teilbaum mit der Wurzel 10 gilt, dass der rechte Subbaum (mit Wurzel 14) eine Höhe von $1$ ($=\max(0,-1)+1$) und der linke (leere Subbaum) eine Höhe von $-1$ haben. Sie unterscheiden sich also um mehr als $1$.
Rotationen
Man kann zeigen, dass eine Rotation nichts an der Gültigkeit des Binären Suchbaums, also an der Sortierung der Elemente, ändert. Führt man nämlich In-Order Traversal in beiden Fällen durch, so kommt man jeweils auf das gleiche Ergebnis. Dieses Rotationsverfahren kann nun genutzt werden, um die Balancierung (die Höhen der beiden Subbäume) anzupassen, ohne die Sortierung des BST zu verändern. Mitunter sind auch zwei Rotation nach einer Insert-Operation nötig, um die AVL-Baum-Invariante herzustellen.
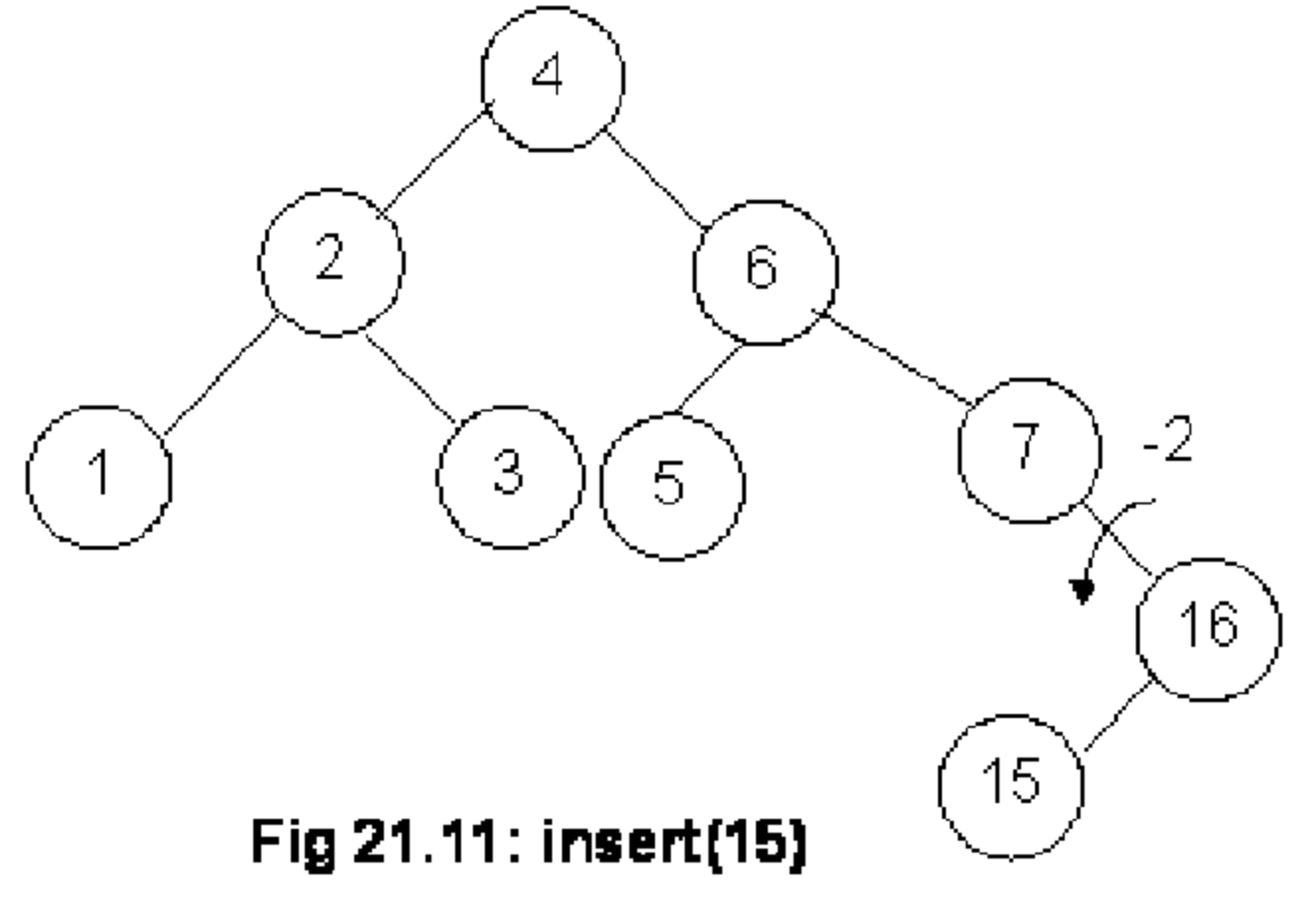
Im folgenden Beispiel wurde zuletzt die $7$ eingefügt. Daraufhin ist die Invariante des AVL-Baums ist verletzt.
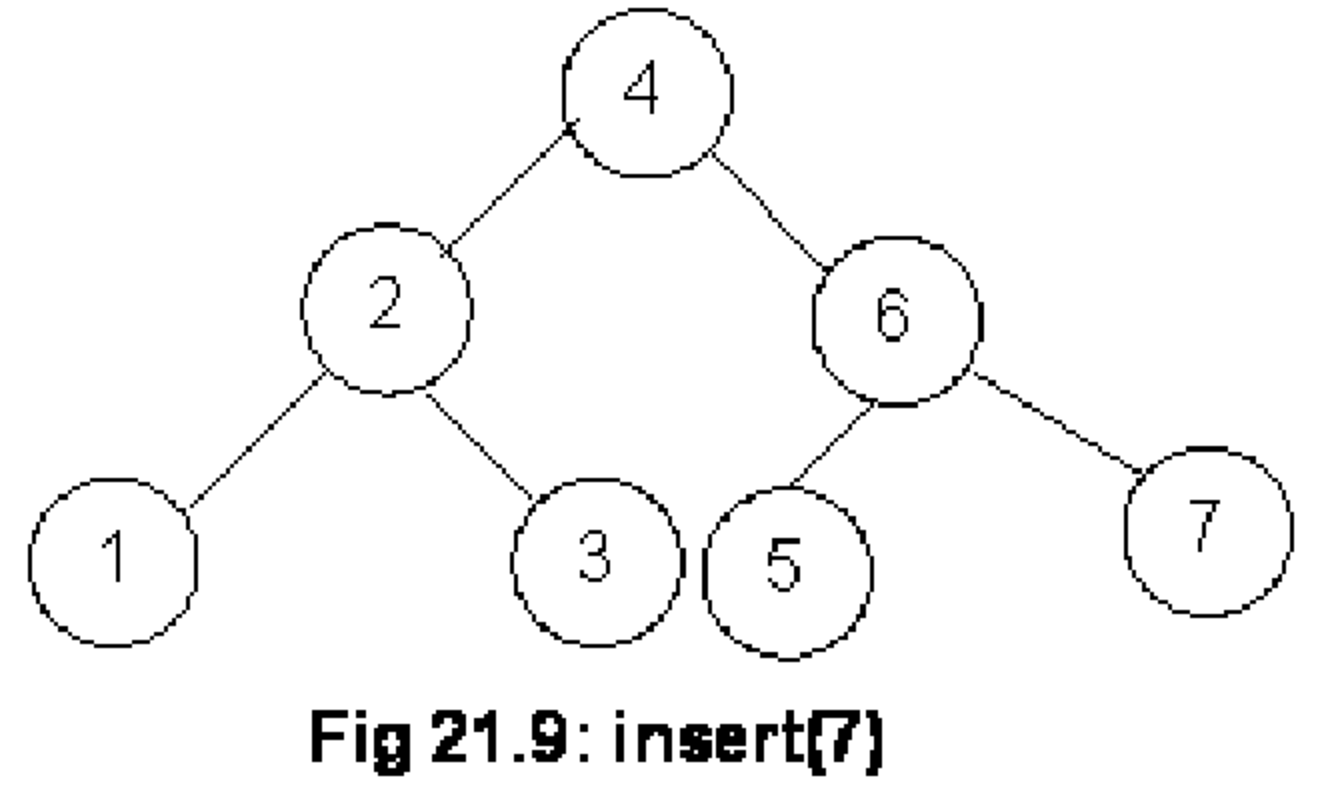
Führt man eine linke Rotation auf dem Knoten mit dem Wert 6 aus, so wird die Invariante wieder erfüllt.
Hier war lediglich eine Rotation nötig, um die Gültigkeit des AVL-Baums wiederherzustellen.
Betrachten wir folgendes Beispiel, so stellen wir fest, dass nun eine Art "Zick-Zack Pfad" existiert.
Hier sind zwei Rotationen, eine sogenannte Doppelrotation (double rotation), nötig. Als erste Rotation wird der Knoten mit dem Wert 15 nach rechts rotiert. Dadurch ergibt sich folgender Zustand:
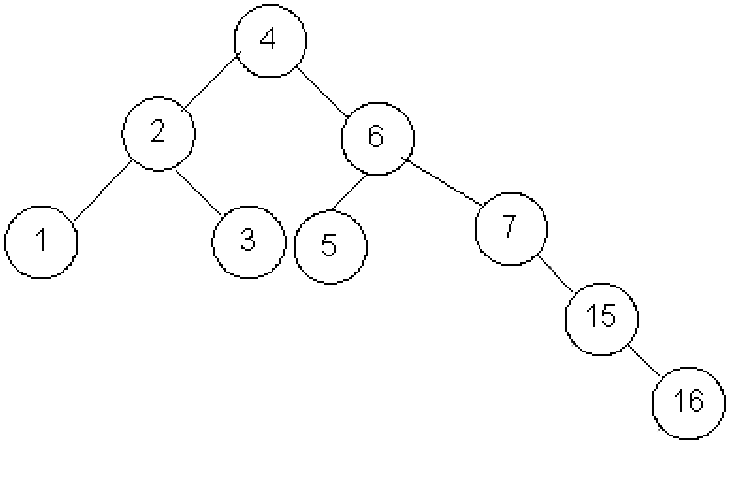
Nun haben wir ein bereits bekanntes Problem und müssen den Knoten mit dem Wert 15 nach links rotieren.
Die Invariante des AVL-Baums gilt nun wieder.
Es gibt also zwei Fälle, bei denen eine Rotation im Baum nötig ist.
Fall 1
Dieser Fall tritt ein, wenn bei einem Knoten der rechte Subbaum um 2 höher ist als der linke Subbaum und das rechte Kind entweder einen um 1 höheren rechten Subbaum hat oder balanciert ist (beide Subbäume sind gleich groß).
Dieser Fall liegt beispielsweise hier vor:
Wie bereits oben beschrieben wurde, ist nun eine linke Rotation auf dem Knoten mit dem Wert 6 nötig.
Dieser Fall 1 tritt ebenfalls ein, wenn bei einem Knoten der linke Subbaum um 2 höher ist als der rechte Subbaum und das linke Kind entweder einen um 1 höheren linken Subbaum hat oder balanciert ist.
Fall 2
Dieser Fall ist der "Zick-Zack"-Fall. Er tritt ein, wenn bei einem Knoten der rechte Subbaum um 2 höher ist als der linke Subbaum und das rechte Kind einen linken Subbaum hat, der um 1 höher ist als der rechte Subbaum. Natürlich gilt das auch entsprechend symmetrisch, also tritt dieser Fall 2 auch ein, wenn bei einem Knoten der linke Subbaum um 2 höher ist als der rechte Subbaum und das linke Kind einen rechten Subbaum hat, der um 1 höher ist als der linke Subbaum.
Dieser Fall wurde ebenfalls oben anhand dieses Beispiels gezeigt:
Es ist eine Doppelrotation nötig.
Komplexitätsanalyse
Der Aufwand zum Suchen beträgt $\mathcal{O}(h)$. Für einen gewöhnlichen BST haben wir festgestellt, dass im worst-case $h = n$ gilt und somit der Aufwand für das Suchen $\mathcal{O}(n)$ ist.
Bei einem AVL-Baum haben wir jedoch folgende Regel, die den Baum bis zu einem gewissen Grad balanciert hält:
$$ \lvert \text{height}(n.\text{right}) - \text{height}(n.\text{left}) \rvert \leqslant 1 $$
Diese Ungleichung kann genutzt werden, um den Aufwand zum Suchen in einem AVL-Baum abzuschätzen. Ein AVL-Baum der Höhe $h$, der die o.g. Regel mit $=1$ (worst case) erfüllt besitzt mindestens $n$ Knoten. Der worst case tritt also ein, wenn sich bei allen Knoten des Baumes die Höhen der Subbäume um 1 unterscheiden. Folglich gibt es zwei worst cases: entweder ist bei allen Knoten der rechte Subbaum um 1 höher als der linke Subbaum oder bei allen Knoten ist der linke Subbaum um 1 höher als der rechte Subbaum.
Nun kann die Anzahl der Knoten $n$ in Abhängigkeit von der Höhe $h$ im worst-case AVL-Baum rekursiv beschrieben werden. Einer der beiden Subbäume - sagen wir der rechte - hat die Höhe $h - 1$. da sich die Höhe des gesamten Baums aus dem Maximum der Höhen der beiden Subbäume addiert mit 1 ergibt. Da der linke Subbaum laut Definition des worst case AVL-Baums eine Höhe hat, die um 1 kleiner als die des rechten Subbaums ist, hat dieser eine Höhe von $h - 2$. Die Anzahl der Knoten eines Baums ist die Anzahl der Knoten der beiden Subbäume addiert mit 1, da der Elternknoten selbst mitgezählt werden muss. Die Elementarfälle treten ein, wenn die Höhe des Baums -1 ist, in diesem Fall besteht er aus keinem Knoten, oder die Höhe des Baums 0 ist, in diesem Fall besteht der Baum aus genau einem Knoten.
$$ n(h) = \begin{cases} 0 , & \text{wenn $h = -1$.} \\ 1 , & \text{wenn $h = 0$.} \\ n(h-1) + n(h-2) + 1 , & \text{sonst.} \end{cases} $$
Aus der rekursiven Beziehung für $h\geq 1$
$$ n(h) = n(h-1) + n(h-2) + 1 $$
folgt mit $n(h-1) > n(h-2)$ die Abschätzung:
$$ \begin{align*} n(h) & > n(h-2) + n(h-2) + 1 \\ & > 2 n(h-2) + 1 \\ & > 2 n(h-2) \\ \end{align*} $$
Wie man der letzten Zeile sofort entnimmt, verdoppelt sich $n$ in jedem Schritt. Dies führt zu folgendem Muster:
$$ \begin{eqnarray} n(h) & = & 2^1\cdot n(h-2\cdot 1) \\ n(h) & = & 2^2\cdot n(h-2\cdot 2) \\ n(h) & = & 2^3\cdot n(h-2\cdot 3) \\ n(h) & = & 2^4\cdot n(h-2\cdot 4) \\ \vdots & = & \vdots \\ n(h) & = & 2^p\cdot n(h-2p) \\ \end{eqnarray} $$
für $p\geq 1$.
Wenn $h=2p$ ist $h-2p=0$ und es wird $n(0)=1$ verwendet. Dann sind $p=\frac{h}{2}$ und
$$ \begin{eqnarray} n & = & 2^p\cdot 1=2^\frac{h}{2}\\ \log_2n & = & \frac{h}{2}\cdot \log_22 = \frac{h}{2}\\ h & = & 2\cdot \log_2n \end{eqnarray} $$
Daraus folgt, dass der Aufwand zum Suchen eines Elements in $\mathcal{O}(\log n)$ liegt.
Zum Einfügen eines Wertes muss zunächst nach einem Element dieses Wertes gesucht werden und danach folgt eine konstante Zahl an Pointeroperationen. Damit ist der Aufwand zum Einfügen $\mathcal{O}(\log n) + \mathcal{O}(1) = \mathcal{O}(\log n)$.
Binäre Heaps
(Binäre) Heaps implementieren den ADT Priority Queue. Eine Priority Queue ist eine lineare Datenstruktur, bei der jedes Element eine Priorität hat und man jederzeit das Element mit der höchsten (bzw. niedrigsten) Priorität abgreifen kann.
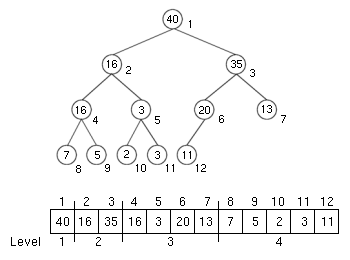
Ein Binärer Heap (binary heap) stellt einen Binärbaum dar, der mit einem Array implementiert wird. Dabei werden die Indices im Baum entsprechend nach Ebene und von links nach rechts durchgezählt. Man beginnt mit 1.
Durch diese Konvention, benötigt man keine spezielle Implementierung des Baums, denn ein Array reicht aus. Ist die Länge des Arrays kleiner als $2^n - 1, n \in \mathbb{N}$, so bleiben in der untersten Ebene Knoten rechts unbesetzt.
Außerdem sind der Elternknoten und die beiden Kinder des Knoten mit dem Index $i$ komfortabel erreichbar.
- Index des Elternknotens des Knotens mit dem Index $i$: $\lfloor \frac{i}{2} \rfloor$ - Index des linken Kindes des Knotens mit dem Index $i$: $2i$ - Index des rechten Kindes des Knotens mit dem Index $i$: $2i+1$
Min-Heap und Max-Heap
Definition 6.8 Bei einem Min-Heap gilt, dass jeder Knoten einen kleineren Wert hat als seine Kinder (sofern er denn Kinder hat).
Definition 6.9 Bei einem Max-Heap gilt, dass jeder Knoten einen größeren Wert hat als seine Kinder (sofern er denn Kinder hat).
Durch diese Tatsache befindet sich bei einem Max-Heap das Element mit dem höchsten Wert in der Wurzel. Der Widerspruchsbeweis ist einfach zu führen: Angenommen das größte Element ist nicht die Wurzel, so hat es einen Elternknoten. Dieser hat auf Grund der Max-Heap Eigenschaft einen höheren Wert. Hier liegt der Widerspruch vor.
Dies und alles folgende für Max-Heaps gilt analog für Min-Heaps.
heapify
heapify ist eine Operation, die auf einem Max- bzw. Min-Heap angewandt werden kann, um eine Verletzung der Max- bzw. Min-Heap Eigenschaft in Ordnung zu bringen.
Wird das Element mit der höchsten Priorität (der Wurzel des Heaps) entnommen, so entsteht im Allgemeinen eine solche Verletzung. Nach der Reparatur wird wieder das Element mit der aktuell höchsten Priorität (in der Wurzel) bereitgestellt. Hier greift die Generatorvorstellung, wenn Anwendungsprogramme auf diese Daten zugreifen. Anders als bei einer Liste, muss die Datenstruktur erst heapified werden, bevor das "nächste" Element generiert werden kann.
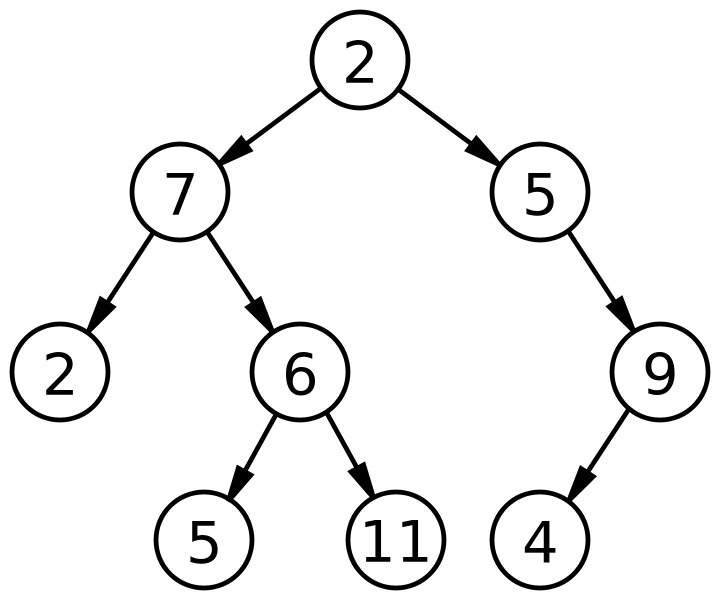
In diesem Beispiel verletzt der Knoten mit dem Index 1 die Max-Heap Eigenschaft. Die Bedingung, damit heapify angewandt werden kann, dass die beiden Subbäume Max-Heaps sind, ist erfüllt. Um die Verletzung der Max-Heap Eigenschaft zu beheben, kann die 3 mit der 10 (der größere Wert der beiden Kinder) vertauscht werden. Nun muss heapify rekursiv auf das Kind aufgerufen werden, dass vertauscht wurde, denn es kann sein, dass durch das Vertauschen die Max-Heap Eigenschaft im Subbaum verletzt wird. Dies ist in dem Beispiel in der Tat der Fall, so dass die 3 mit der 5 vertauscht wird. Der Algorithmus terminiert, sobald die Max-Heap Eigenschaft nicht verletzt ist. Dies ist spätestens beim Blatt der Fall, da er keine Kinder hat und somit die Max-Heap Eigenschaft nicht verletzen kann.
Da sich die Höhe $h$ des Baums durch $\log n$ aus der Anzahl $n$ der Elemente ergibt und maximal $h$-mal heapify mit einem konstanten Aufwand aufgerufen wird, beträgt die Zeitkomplexität für heapify $\mathcal{O}(\log n)$.
build max-heap
build max-heap ist eine Operation, mit der man ein beliebiges unsortiertes Array so umsortiert, dass anschließend die Max-Heap Eigenschaft hergestellt ist.
Bei diesem Algorithmus wird auf dem Eingabearray mit der Länge $n$ von $\lfloor \frac{n}{2} \rfloor$ bis 1, in dieser Reihenfolge, die max-heapify Operation aufgerufen. Es reicht aus bei $\lfloor \frac{n}{2} \rfloor$ anzufangen, da alle Elemente nach $\lfloor \frac{n}{2} \rfloor$ keine Kinder haben und demnach die Max-Heap Eigenschaft an diesem Knoten nicht verletzt sein kann. Dies ist einfach zu verifizieren, da der letzte Knoten den Index $n$ hat und somit sein Elternknoten per Heap-Definition den Index $\lfloor \frac{n}{2} \rfloor$. Dieser Elternknoten ist der letzte Knoten, der ein Kind hat, da alle weiteren Knoten Kinder mit einem Index haben, der außerhalb des Arrays liegt. Dadurch, dass man rückwärts iteriert, ist sichergestellt, dass an den beiden Kindern die Max-Heap Eigenschaft gilt, da es entweder Blätter sind oder die Kinder bereits abgearbeitet wurden, da sie einen höheren Index haben.
Komplexitätsanalyse
Es werden in der Schleife $\mathcal{O}(n)$ Iterationen durchgeführt. Die heapify Operation hat einen Aufwand von $\mathcal{O}(\log n)$. Damit beträgt der Zeitaufwand für build max-heap Operation $\mathcal{O}(n \log n)$.
Dies kann jedoch noch etwas genauer untersucht werden. Genau genommen beträgt der Aufwand für heapify $\mathcal{O}(l)$. $l$ ist dabei das Level, von unten gezählt, auf welchem sich der Knoten befindet. Es ist ersichtlich, dass es $\frac{n}{4}$ Knoten mit Level 1 gibt, $\frac{n}{8}$ Knoten mit Level 2, $\frac{n}{16}$ Knoten mit Level 3, $\dotsc$ und einen Knoten mit Level $\log n$. Auf Grund dieser Tatsache können wir eine Summe definieren, die den Gesamtaufwand für die Schleife angibt.
$$ T(n) = \frac{n}{4} (1 \cdot c) + \frac{n}{8} (2 \cdot c) + \frac{n}{16} (3 \cdot c) + \dotsc + 1 (\log n \cdot c) $$
Die Konstante $c$ ist dabei eine beliebige Konstante, die den Aufwand für heapify an einem Knoten beschreibt.
Da es sich bei den Brüchen immer um Zweierpotenzen handelt, können wir $\frac{n}{4} = 2^k$ setzen und $c$ ausklammern, um den Ausdruck zu vereinfachen.
$$ \begin{align*} T(n) & = c \cdot 2^k \left(\frac{1}{2^0} + \frac{2}{2^1} + \frac{3}{2^2} + \dotsc + \frac{k+1}{2^k} \right) \\ & = c \cdot 2^k \sum_{i=0}^{k} \frac{i+1}{2^i} \end{align*} $$
Mit Hilfe des Quotientenkriteriums kann man zeigen, dass die Reihe $$ \lim_{k \to \infty} \sum_{i=0}^{k} \frac{i+1}{2^i} $$ konvergiert und somit eine Konstante darstellt.
$$ L = \lim_{n \to \infty} \left| \frac{a_{n+1}}{a_n} \right| = \lim_{n \to \infty} \left| \frac{\frac{n+2}{2^{n+1}}}{\frac{n+1}{2^n}} \right| = \lim_{n \to \infty} \left| \frac{n+2}{2^{n+1}} \cdot \frac{2^n}{n+1} \right| = \lim_{n \to \infty} \left| \frac{n+2}{2 \cdot 2^n} \cdot \frac{2^n}{n+1} \right| = \lim_{n \to \infty} \left| \frac{n+2}{2n+2} \right| = \frac{1}{2} < 1 \implies \lim_{k \to \infty} \sum_{i=0}^{k} \frac{i+1}{2^i}=d \text{ (konvergent)} $$
$$ T(n) = c \cdot 2^k \cdot d = c \cdot d \cdot \frac{n}{4} \in \mathcal{O}(n) $$
Es kann also mit $\mathcal{O}(n)$ eine kleinere obere Schranke für die build max-heap Operation angegeben werden.
Heap Sort
Die Heap Datenstruktur kann für ein effizientes Sortierverfahren genutzt werden. Dafür wird nach build max-heap entsprechend die Max-Heap Struktur von dem zu sortierenden Array erstellt. Es ist nun klar, dass das größte Element in der Wurzel ist, also in A[1] und demnach direkt dem Heap entnommen werden kann. Diese Lücke wird gefüllt, indem das Element A[n] nun an die Stelle von A[1] gesetzt wird. Nun muss die Max-Heap Struktur mit max-heapify wiederhergestellt werden. Dieser Vorgang wird $n$-mal wiederholt, bis alle Elemente entsprechend sortiert dem Heap entnommen wurden.
Die build max-heap Operation hat, wie oben gezeigt wurde, einen Aufwand von $\mathcal{O}(n)$. Der Aufwand innerhalb der Schleife ist durch den Aufwand von heapify bestimmt. Dieser ist $\mathcal{O}(\log n)$. In der Schleife gibt es $n$ Iterationen. Demnach ist der Aufwand für Heap Sort $\mathcal{O}(n) + \mathcal{O}(n \log n) = \mathcal{O}(n \log n)$.