Greedy Algorithmen
Aus ProgrammingWiki
Gierige Algorithmen werden immer dann verwendet, wenn eine Lösung auf direktem Weg erreicht werden kann. Eine aktuell vorliegende momentante Situation (lokale Informationen) wird dabei schrittweise verbessert, d.h. der Algorithmus nimmt sich in jedem Schritt den "besten Happen" (greedy = gierig). Von einer einmal verbesserten Situation gibt es keinen Weg zurück: Kein Backtracking - das verspricht gute Effizienz. Es werden auch keine Alternativen betrachtet. Kann eine Situation nicht weiter verbessert werden, steht das Ergebnis fest.
Nicht alle Probleme können mit Greedy Algorithmen (exakt) gelöst werden. Aber oftmals sind Näherungslösungen machbar, die sehr effizient ermittelt werden können. In der Praxis ist die benötigte Zeit oft das wichtigere Kriterium. Im Folgenden werden einige Greedy-Algorithmen vorgestellt, die exakte Lösungen produzieren.
Inhaltsverzeichnis |
Bruchteilrucksack
Im Gegensatz zum 0/1-Rucksackproblem, ist es beim Bruchteilrucksack erlaubt, auch Bruchteile von Gegenständen einzupacken. Werden 80 Prozent eines Gegenstands eingepackt, heißt das nichts anderes als das 80 Prozent seines Gewichts den Rucksack belasten und 80 Prozent seines Wertes den Rucksackwert erhöhen.
Man kann den Rucksack exakt bis zu seiner Kapazitätsgrenze zu füllen. Es ist klar, dass Gegenstände mit hohem Wert und geringem Gewicht zu bevorzugen sind. Sortiert man die Gegenstände nach dem spezifischen Gewicht ($\frac{\text{Gewicht}}{\text{Wert}}$) aufsteigend, so erhält man eine priorisierte Liste. Der Gegenstand mit dem kleinsten spezifischen Gewicht ist der beste und steht deshalb ganz vorn, wird also als erster eingepackt (falls möglich). Durch das spezifische Gewicht werden die Gegenstände vergleichbar, denn es sagt aus, wie schwer der Gegenstand pro Werteinheit ist. (Alternativ kann auch der spezifische Wert (Wert pro Gewichtseinheit) für eine absteigende Sortierung genutzt werden.) Die Gegenstände können nun, solange die Kapazitätsgrenze nicht überschritten wird, genau in der Reihenfolge ihrer Sortierung in den Rucksack gelegt werden. Der übrige Platz kann dann durch einen entsprechenden Bruchteil des nächsten Gegenstands aufgefüllt werden. Es wird an keiner Stelle ein Gegenstand wieder aus dem Rucksack entfernt und es gibt kein Probieren. Die Lösung wird direkt angesteuert.
Hinweis: Das 0/1 Rucksackproblem ist mit der Greedy Strategie nicht (exakt) lösbar. Die Gegenstände nach ihrem spezifischen Gewicht nacheinander einzupacken führt hier nicht immer zum optimalen Rucksack. Stünden z.B. ein Diamant (Wert 1000, Gewicht 90) und fünf Goldmünzen (jeweils Wert 210, Gewicht 20) für einen Rucksack, der ein Gewicht von 100 tragen kann, zur Auswahl, würde der Greedy Algorithmus den Diamanten einpacken und einen Rucksackwert von 1000 erreichen. Die exakte Lösung besteht jedoch darin, stattdessen die fünf Goldmünzen zu nehmen (Wert 5 x 210 = 1050).
Geldwechselproblem
Beim Geldwechselproblem kann ganz ähnlich vorgegangen werden wie beim Bruchteilrucksack. Hier geht es darum, einen Geldbetrag in möglichst wenige Münzen einzutauschen. Der Betrag kann hier wie die Maximalkapazität beim Rucksackproblem behandelt werden. Die möglichen Münzen stellen bei dieser Analogie die Gegenstände dar. Der einzige Unterschied besteht darin, dass Münzen mehrfach ausgewählt werden können.
Nach absteigender Sortierung der möglichen Münzwerte wird nach und nach versucht den jeweils größten vom aktuellen Betrag abzuziehen. Wenn dies möglich ist, so wird die Münze dem Ergebnis hinzugefügt. Anderenfalls wird die Münze mit diesem Wert aus der Kandidatenliste entfernt, sodass im nächsten Durchlauf der nächstkleinere Münzwert verwendet wird. Das folgende Programm zeigt auch, dass eine rekursive Implementation von Greedy Algorithmen möglich ist.
Für das Geldwechselproblem gibt es neben dem hier behandelten Greedy-Algorithmus auch ein Verfahren nach dem Prinzip des dynamischen Programmierens.
Minimal aufspannender Baum (MST)
Die beiden folgenden Algorithmen erzeugen zu jedem zusammenhängenden, ungerichteten und kantengewichteten Graphen einen minimalen Spannbaum.
Zur Wiederholung: Ein aufspannender Baum eines zusammenhängenden Graphen $G=(E,V)$ ist ein Baum, d.h. ein kreisfreier und zusammenhängender Teilgraph $G'=(V',E')$ mit $V'=V$ und $E'\subseteq E$. "kreisfrei" bedeutet eine Knotenfolge ohne Knotenwiederholung mit Ausnahme des Start- und Endeknotens.
Intuitiv kann man sich einen Spannbaum als einen Graph vorstellen, dessen sämtliche Knoten mit "angehoben" werden, wenn man genau einen beliebigen Knoten "hochhebt", ohne dass überflüssige Kanten existieren. Praktische Anwendungen gibt es: So sollte der Leitungsweg, um bei einer bestimmten Verkabelung alle Knoten (Orte) zu erreichen, minimal sein, um Materialkosten zu sparen.
Dabei kommt der Minimal aufspannende Baum (= minimal spanning tree = MST) ins Spiel. Das Gesamtgewicht des MST soll minimal sein. (Das Ganze gibt es auch in der Maximalvariante, dann aber mit anderer praktischer Anwendung!)
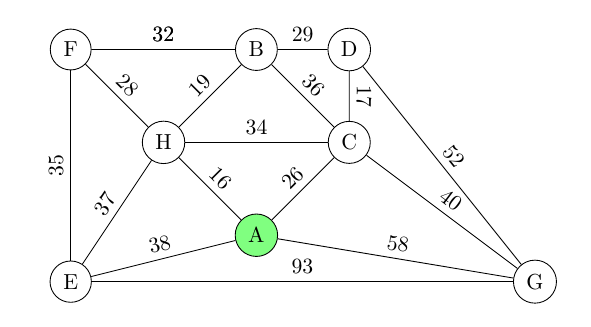
Beispiel: Beide Verfahren werden auf den folgenden Graphen angewandt.
KRUSKAL-Algorithmus
Das auf Joseph KRUSKAL (1956) zurückgehende Verfahren zur Bestimmung des MST beginnt mit der Übernahme aller Knoten von $G$. Danach werden die Kanten nach ihrem Gewicht aufsteigend sortiert und in dieser Reihenfolge schrittweise hinzugefügt, sofern dabei kein Kreis (s. auch zyklussuche) entsteht. Würde sich ein Kreis ergeben, wird die betreffende Kante übergangen und die jeweils nächste verwendet. Haben mehrere Kanten das gleiche Gewicht, kann eine davon zufällig ausgewählt werden.
Das Verfahren arbeitet mit $\mathcal{O}(|E|\log(|E|))$, wobei $|E|$ die Anzahl der Kanten des Graphen bedeutet. Ist die Prüfung auf Kreisfreiheit geeignet implementiert, so schlägt vor allem die Sortierung ins Gewicht, was den o.g. Wert ergibt. Besitzt ein Graph sehr viele Kanten, so ist der Algorithmus von Prim (nächster Abschnitt) vorzuziehen, da er ohne Sortierung auskommt.
Beispiel: Wir beziehen uns auf den in Abb. 1 angegebenen Beispielgraph.
Die folgenden nach ihrem Gewicht aufsteigend sortierten Kanten werden dem Graph schrittweise hinzugefügt. Die Kanten, die zu einem Kreis führen würden, sind mit eckigen Klammern gekennzeichnet.
AH-16, CD-17, BH-19, AC-26, FH-28, [BD-29], [BF-32], [HC-34], EF-35, [BC-36], [EH-37], [AE-38], CG-40, [DG-52], [AG-58], [EG-93]
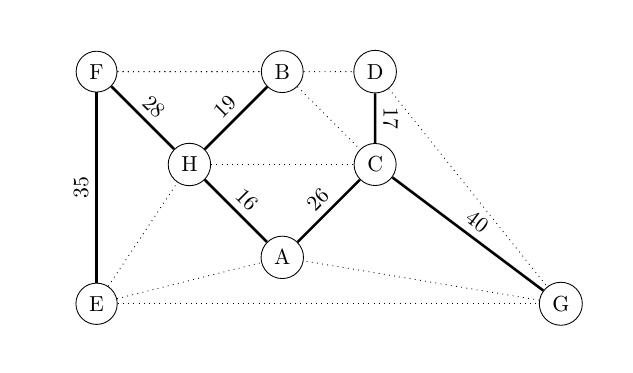
Im Ergebnis erhalten wir den folgenden MST für den oben angegebenen Graphen. Das minimale Gesamtgewicht beträgt 181.
Algorithmus von Prim
Der Algorithmus wurde 1930 vom tschechischen Mathematiker Vojtěch Jarník entwickelt. 1957 wurde er zunächst von Robert C. Prim und dann 1959 von Edsger W. Dijkstra wiederentdeckt. Dieses Greedyverfahren hat Ähnlichkeiten mit der Breitensuche (und mit dem weiter unten betrachteten Dijkstra-Algorithmus).
Während das Verfahren von Kruskal wie oben beschrieben Kanten-orientiert arbeitet, schreitet Prim in erster Linie Knoten-orientiert voran.
Der Algorithmus beginnt mit einem trivialen Graphen $T=(V',E')$, der zunächst aus genau einem beliebigen Knoten des gegebenen Graphen $G=(V,E)$ besteht. In jedem Schritt wird eine inzidierende Kante mit minimalem Gewicht gesucht, die einen weiteren bisher noch nicht zu $V'$ gehörenden Knoten mit einem zu $V'$ gehörenden verbindet. Diese Kante und der zugehörige Knoten werden zu $T$ hinzugefügt. Dies wird solange wiederholt, bis alle Knoten aus $V$ in $V'$ vorhanden sind; dann ist $T$ ein minimaler Spannbaum. (Natürlich gibt es eine formale Beweispflicht für die Korrektheit des Verfahrens.)
Im Unterschied zum Kruskal-Algorithmus, bei dem die Kreisfreiheit explizit geprüft wird, vermeidet Prim die Bildung von Kreisen konstruktiv. Beim Prim-Algorithmus muss der sich aufbauende Teilgraph (MST) zu jedem Zeitpunkt zusammenhängen.
Der Gesamtaufwand des Verfahrens (bei geschickter Implementierung der Prioritätswarteschlange mit Fibonacci-Heaps) beträgt $\mathcal{O}(|E|+|V|\log |V|)$ mit Bezug auf den gegebenen Graphen $G=(V,E)$.
Beispiel: Wir beziehen uns auf den in Abb. 1 angegebenen Beispielgraph.
Die folgende Übersicht zeigt die einzelnen Schritte bis alle Knoten in die Knotenmenge $V'$ des MST $T$ gewandert sind. Links vermerken wir $V'$, wobei der jeweils rechts in der Menge angegebene Knoten in diesem Schritt hinzugekommen ist. Rechts sind die im nächsten Schritt infrage kommenden Kanten (zusammen mit ihrem Gewicht) angegeben. Die zur Benennung einer (ungerichteten) Kante verwendete Knotenreihenfolge spielt keine Rolle. Die mit ** hervorgehobene Kante wird ausgewählt. Der Startknoten ist beliebig wählbar; wir beginnen bei $A$.
V'=... Kanten (x, y) mit x aus V' und y aus V\V'
------------------------------------------------------------------------------------
{A}: AE-38, **AH-16**, AC-26, AG-58
{A,H}: HE-37, HF-28, **HB-19**, HC-34, AE-38, AC-26, AG-58
{A,H,B}: BF-32, BC-36, BD-29, HE-37, HF-28, HC-34, AE-38, **AC-26**, AG-58
{A,H,B,C}: **CD-17**, CG-40, BF-32, BD-29, HE-37, HF-28, AE-38, AG-58
{A,H,B,C,D}: DG-52, CG-40, BF-32, HE-37, **HF-28**, AE-38, AG-58
{A,H,B,C,D,F}: **FE-35**, DG-52, CG-40, HE-37, AE-38, AG-58
{A,H,B,C,D,F,E}: EG-93, DG-52, **CG-40**, AG-58
{A,H,B,C,D,F,E,G}: ---
Im Ergebnis erhalten wir den folgenden MST für den oben angegebenen Graphen. Das minimale Gesamtgewicht beträgt 181.
Kürzeste Wege
Algorithmus von Dijkstra
Der Dijkstra-Algorithmus zur Suche nach kürzesten Wegen zwischen zwei Knoten ist auf un/gerichtete und un/gewichtete zusammenhängende Graphen anwendbar, wenn sämtliche ggf. vorhandenen Kantengewichte nichtnegativ sind. Für die Suche nach kürzesten Wegen in Graphen, die auch negative Kantengewichte haben können, eignet sich der Bellman-Ford-Algorithmus. Dieser beruht auf dem algorithmischen Entwurfskonzept des dynamischen Programmierens. Der Algorithmus von Dijkstra folgt der Greedy-Strategie, ein momentanes Zwischenergebnis durch Hinzunahme "des jeweils besten Happens" schrittweise zu verbessern ohne eine getroffene Entscheidung zu revidieren.
Als Nebenprodukt erhält man alle kürzesten Wege von einem gewählten Startknoten zu jedem anderen Knoten des Graphen.
Im Gegensatz zum TSP (Traveling Salesman Problem), bei dem eine kürzeste Rundreise (im Graphen als Kreis zu finden) nur in exponentieller Zeit gefunden werden kann, ist das Finden des kürzesten Weges zwischen zwei Knoten eines (gerichteten oder ungerichteten) gewichteten Graphen recht effizient in $\mathcal{O}(|V|^2)$ möglich. Wählt man Fibonacci-Heaps für die Implementation der Prioritätswarteschlange, ergibt sich ein Aufwand von $\mathcal{O}(|E|+|V|\log(|V|))$.
Beschreibung des Dijkstra-Algorithmus
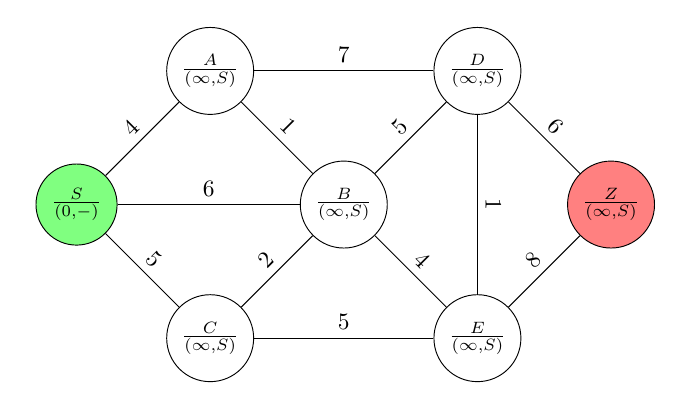
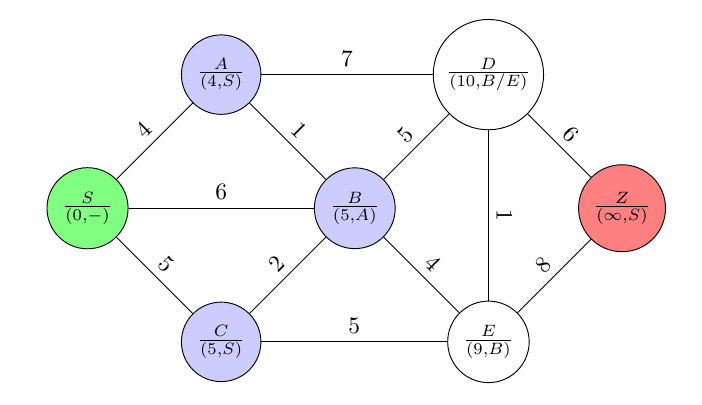
Beispiel: Gegeben ist der folgende ungerichtete Graph mit den angegebenen Kantengewichten. Gesucht ist der kürzeste Weg von $S$ nach $Z$.
Die in jedem Knoten $K$ hinzugefügte Markierung $(e,X)$ gibt die Länge $e$ des (bisher) kürzesten Weges vom Startknoten $S$ zu $K$ an. Auf diesem Weg ist $X$ der unmittelbare Vorgänger von $K$.
Nach der Initialisierung ergeben sich die folgenden Markierungen.
Für die Nachbarknoten ($A$, $B$ und $C$) des aktuellen Knotens $S$ (zu Beginn der Startknoten) erhalten wir
und $S$ wird in der Menge noch einbeziehbarer Knoten gestrichen bzw. in eine Ergebnisliste verschoben (Greedy-Schritt).
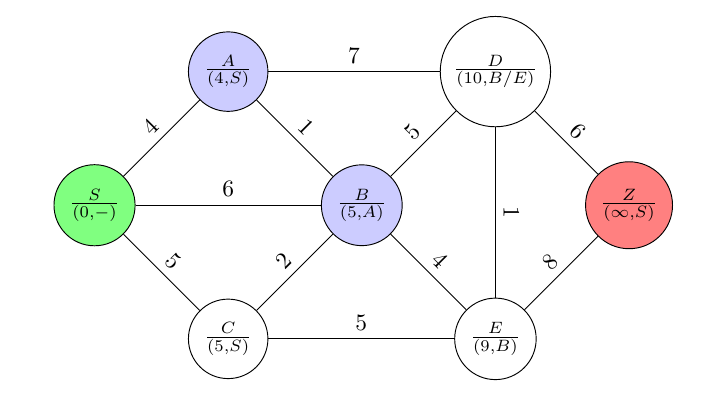
Aus allen verfügbaren Knoten wählt man den mit der geringsten Entfernung (dem kürzesten Weg) zu $S$ aus. Das ist $A$ in unserem Beispiel. Dieser nun aktuelle Knoten wird in der Abbildung blau gefärbt. Anschließend werden die Markierungen der noch ungefärbten Nachbarn von $A$, also $B$ und $D$, aktualisiert. Die $(6,S)$-Markierung von $B$ muss der $(5,A)$-Markierung weichen, denn der Weg von $S$ über $A$ zu $B$ ist kürzer ($5$) als der direkte ($6$).
$A$ wird in der Menge noch einbeziehbarer Knoten gestrichen bzw. in eine Ergebnisliste verschoben.
Für den nächsten aktuellen Knoten gibt es zwei Kandidaten, nämlich $B$ und $C$, denn beide haben die gleiche minimale Distanz ($5$) zu $S$. Die Entscheidung kann zufällig oder auch implementationsabhängig stattfinden. Wir wählen $B$. Die noch ungefärbten Nachbarknoten von $B$ sind $C$, $D$ und $E$. Eine neue Markierung für $C$ wird nicht vorgenommen, da die bestehende mit $(5,S)$ besser ist als $(7,A)$, d.h. der direkte Weg von $S$ zu $C$ ist kürzer als der Weg über $A$.
$B$ wird in die Ergebnisliste verschoben.
Der unter den bisher noch ungefärbten Knoten ist $C$ der mit der aktuell kürzesten Entfernung zu $S$. Deshalb geht es mit $C$ als aktuellen Knoten weiter. Die Markierung von $E$ wird nicht verändert.
$C$ wird gestrichen, d.h. in die Ergebnisliste verschoben.
Im nächsten Schritt ist $E$ der aktuelle Knoten. Dessen Nachfolgerknoten $Z$ erhält jetzt eine neue Markierung, nämlich $(17,E)$. $E$ wird gestrichen, d.h. in die Ergebnisliste verschoben.
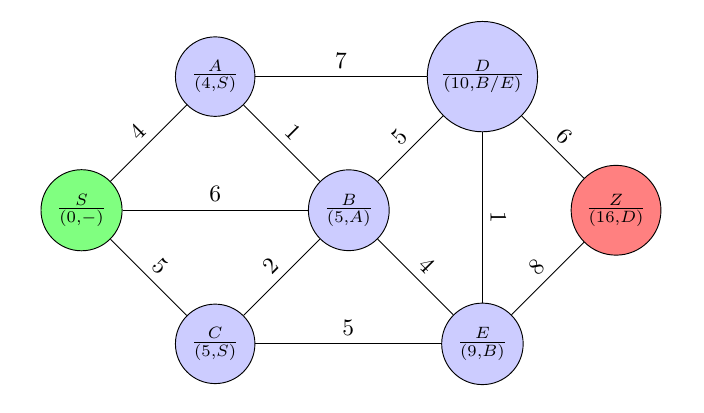
Und schließlich kommt $D$ an die Reihe. Dessen Nachfolgerknoten $Z$ verbessert sich zu $(16,D)$.
$D$ wird gestrichen, d.h. in die Ergebnisliste verschoben.
Im letzten Schritt werden die Markierungen der Nachfolgerknoten von $Z$ aktualisiert. Da sämtliche Nachbarknoten von $Z$ eingefärbt sind und damit nicht mehr zur Verfügung stehen, ist nichts zu tun.
Schließlich wird $Z$ gestrichen, d.h. in die Ergebnisliste verschoben.
Damit ist klar, dass der kürzeste Weg von $S$ zu $Z$ genau $16$ beträgt. Man kann ihn leicht rekonstruieren, indem man die Knotenmarkierungen (Ergebnisliste) rückwärts, d.h. mit $Z$ beginnend, verfolgt. Aus den Knotenmarkierungen geht der jeweilige Vorgängerknoten unmittelbar hervor: $S\rightarrow A\rightarrow B\rightarrow D\rightarrow Z$ bzw. $S\rightarrow A\rightarrow B\rightarrow E\rightarrow D\rightarrow Z$. Die Addition der Gewichte der einbezogenen Kanten ergibt gerade $16$.
Als Nebenprodukt ergeben sich die Längen aller minimalen Wege von $S$ zu je einem Knoten:
S A C B D E Z ------------------------ S 0 4 5 5 10 9 16
Die Länge des kürzesten Weges von $S$ zu $D$ beträgt demnach $10$ und der von $S$ zu $E$ $9$.
Rückblickend betonen wir, dass eine explizite Sortierung der Kandidatenliste beim Dijkstra-Verfahren nicht vorgenommen wird. Dies geschieht implizit, d.h. es ist im Verfahren eingebaut. Außerdem gilt das Bellmansche Optimalitätsprinzip, da man in jedem Schritt die aktuell kürzeste Distanz des Vorgängerknotens zum Startknoten verwendet. Dieses Optimalitätskriterium ist Kern des dynamischen Programmierens, sodass mit Dijkstra ein Greedy Algorithmus mit Eigenschaften des dynamischen Programmierens vorliegt.
Man kann zeigen, dass ein Greedy-Verfahren ein Optimierungsproblem exakt lösen kann, wenn die zugrunde liegende algebraische Struktur ein gewichteter Matroid ist. Anderenfalls ergibt sich im Allgemeinen eine gute Näherungslösung.
Implementation
Den Graph aus dem obigen Beispiel implementieren wir mittels Adjazenzliste.
Wir brauchen ein paar Konstanten: für eine sehr große natürliche Zahl, die de facto eine nicht vorhandene Verbindung zwischen zwei Knoten repräsentiert, eine für den Start- und eine für den Zielknoten des betrachteten Graphen.
Für die Menge der jeweils noch ungefärbten Knoten legen wir ein zunächst leeres Dictionary greedy_list an, dessen Element den Aufbau { vertex : [distance_S, predecessor], ... } haben.
Darauf lassen sich nützliche Operationen anwenden: Das Gewicht der Kante zwischen $D$ und $E$ beträgt
Die adjazenten Knoten von $E$ sind
Nun kann der globalen Variablen greedy_list der sich aus dem Graph ergebende Initialwert für graph0 zugewiesen werden.
Den Wert eines Knotens in greedy_list erhält man mittels
und den Knoten in greedy_list mit dem kleinsten Wert liefert
Jetzt folgt der spannende Teil, nämlich das Aktualisieren der Markierungen aller Nachbarknoten des Knotens $R$ in greedy_list mit kleinstem Wert. Im Falle einer Verbesserung (Weglängenverkürzung) wird die neue Markierung im Dictionary einfach zugewiesen, wodurch die vorherige verschwindet. Anderenfalls bleibt sie einfach unverändert.
Anschließend wird $R$ aus der Liste der annotierten Knoten entfernt, was dem Einfärben in obiger Erklärung entspricht.
def greedy_list_aktualisieren(graph, R): # R ist vertex in greedy_list mit min. Dist. zu START
global greedy_list
for Y in nachbarn(graph, R):
if Y in greedy_list:
h = wert(R) + gewicht(graph, R, Y)
if h < wert(Y):
greedy_list[Y] = [h, R] # neue Markierung
print('Streiche :', R, greedy_list[R])
del greedy_list[R] # Knoten R wird aus greedy_list entfernt
Die Funktion Dijkstra sorgt dafür, dass dieser schrittweise ablaufende Prozess solange stattfindet, wie sich der Zielknoten ZIEL in greedy_list befindet:
def Dijkstra(graph):
global greedy_list
greedy_list = greedy_list_generieren(graph)
while ZIEL in greedy_list:
greedy_list_aktualisieren(graph, bestimme_r())
Übungsaufgaben
Übungsaufgabe 1: Nehmen Sie sich die folgende Adjazenzlistenrepräsentation graph01 des Graphen $G_1$ vor und zeichnen Sie $G_1$.
graph1 = {"A" : [("B", 4), ("C", 9), ("E", 10), ("F", 6)],
"B" : [("A", 4), ("C", 3), ("G", 5), ("F", 6)],
"C" : [("B", 3), ("G", 6), ("D", 8), ("A", 9)],
"D" : [("C", 8), ("G", 3), ("E", 3), ("F", 9)],
"E" : [("A", 10), ("D", 3),],
"F" : [("A", 6), ("G", 7), ("D", 9), ("F", 6)],
"G" : [("F", 7), ("B", 5), ("C", 6), ("D", 3)],
}
Bestimmen Sie den kürzesten Weg von $A$ nach $D$. Vergleichen Sie Ihr ermitteltes Ergebnis mit dem des Programms:
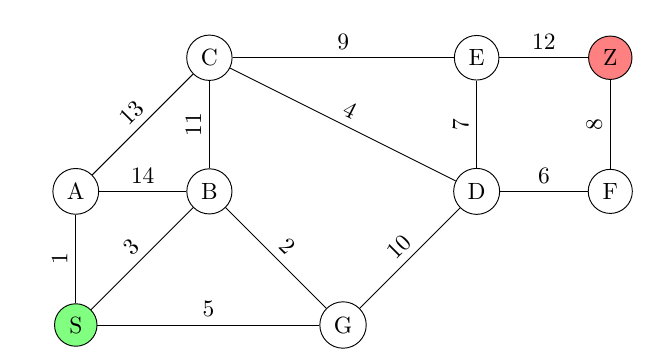
Übungsaufgabe 2: Ermitteln Sie den kürzesten Weg ($12$) von $S$ zu $Z$ mit dem Dijkstra-Algorithmus und geben Sie dessen Länge an.
Lösung: Der Weg $S\rightarrow B\rightarrow A\rightarrow C\rightarrow E\rightarrow Z$ hat eine Länge von $19$.
Übungsaufgabe 2: Ermitteln Sie den kürzesten Weg von $S$ zu $Z$ mit dem Dijkstra-Algorithmus und geben Sie dessen Länge an. graph2 ist bereits angelegt.
Lösung: Der Weg $S\rightarrow G\rightarrow D\rightarrow F\rightarrow Z$ hat eine Länge von $29$.
Beschreibung des Dijkstra-Algorithmus - Variante 2
Wir geben noch eine studentische Erklärung des Verfahren in enger Verbindung mit einem (anderen) Beispiel an.
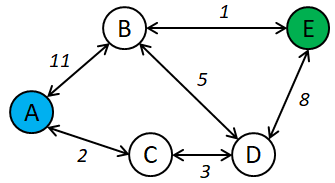
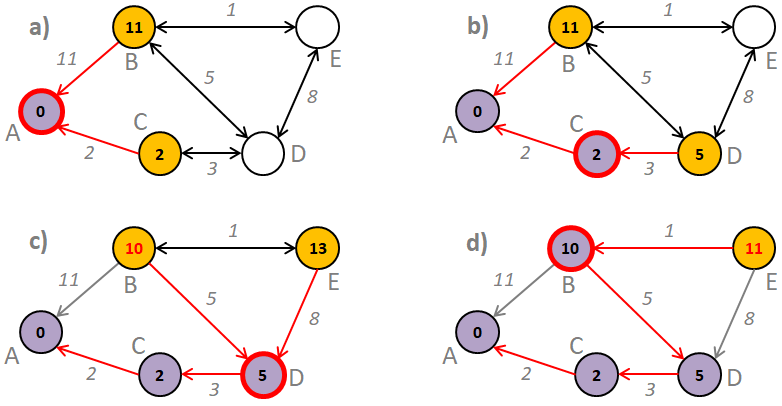
Beispiel: In folgendem Graph soll der kürzeste Weg von A nach E gefunden werden.
Ausgehend vom Startpunkt A werden zunächst alle (adjazenten) Nachbarknoten ermittelt und an diesen die Länge des Weges von A bis dorthin hinterlegt (Bild a). Zusätzlich merkt man sich den Vorgängerknoten von dem aus dieser Weg beschritten wurde (rote Pfeile). Im weiteren Verlauf wird nun unter den noch nicht verarbeiteten Knoten der mit dem kürzesten hinterlegten Weg untersucht (das beste momentane Zwischenergebnis, in Bild b Knoten C) und dessen angrenzende Knoten ermittelt (nur Knoten D, da A bereits verarbeitet wurde). Der am untersuchten Knoten (C) hinterlegte Weg (der kürzeste Weg vom Startknoten bis dahin, bei Knoten C die Länge 2), erweitert um den Weg bis zum angrenzenden Knoten (3 bis nach D), wird nun mit dem am angrenzenden Knoten hinterlegten Weg (der bisher kürzeste Weg vom Startknoten bis zu diesem) verglichen. Gibt es noch keinen hinterlegten Wert, so kann die momentan berechnete Länge gespeichert werden (in Bild b Speicherung von 5 zu Knoten D). Ist der momentane Weg kürzer als der bereits am angrenzenden Knoten hinterlegte Weg, dann wird dieser ersetzt (Verbesserung des Zwischenergebnisses*, in Bild c passiert das mit Knoten B). Im gleichen Zuge wird auch der Vorgänger entsprechend geändert. Bild d zeigt, dass genau das Gleiche bei Knoten E passiert.
Sobald der Zielknoten derjenige mit dem geringsten hinterlegten Weg ist, ist klar, dass dieser der Knoten mit der momentan kürzesten Distanz zum Startknoten ist. Es kann demzufolge keine kürzere Distanz zum Startknoten geben und der kürzeste Weg (hier von A nach E: A-C-D-B-E) ist gefunden. Da an jedem Knoten der Vorgänger hinterlegt wurde von dem aus dieser kürzeste Weg zustande gekommen ist, kann durch Verfolgung der Vorgänger bis hin zum Startknoten der Weg rekonstruiert werden.
Schlussendlich wird bei dieser Vorgehensweise jeder Knoten nur maximal einmal untersucht und bei jedem Besuch werden nur die noch nicht untersuchten Knoten aktualisiert, sofern sie vom aktuellen Knoten aus überhaupt erreichbar sind.
Folgendes Programm nutzt eine Entfernungsmatrix, um den Graphen zu repräsentieren. Diese enthält in jedem Feld die Entfernung von einem Ausgangsknoten (Zeilenindex) zu einem Zielknoten (Spaltenindex). Für Knoten die keine direkte Verbindung haben, wird eine Entfernung von Unendlich (> inf) definiert. In der nach der hinterlegten Distanz sortierten Ausgangsknotenliste > nodes wird der Startknoten mit einer Distanz von 0 markiert, sodass in der äußeren > while-Schleife mit diesem begonnen wird. Solange der Knoten mit der kürzestesten Distanz zum Startknoten (> n) noch nicht der Zielknoten (Knotenindex > end) ist, werden die verbleibenden Knoten (> nn) aktualisiert. Durch Nutzung von > heapq werden die verbleibenden Knoten (> nodes) stets nach ihrer hinterlegten Mindestdistanz zum Startknoten sortiert.
([0, 2, 3, 1, 4], 11)
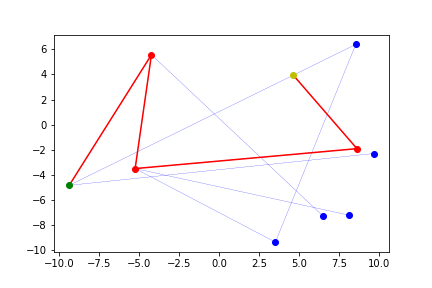
Folgendes Programm nutzt den Dijkstra Algorithmus, um die kürzeste Verbindung zweier Punkte in einem Graphen zu finden. Graphen werden hier zufällig generiert und grafisch dargestellt, sodass eine visuelle Kontrolle erfolgen kann.