Mehrfachrekursionen

Aus ProgrammingWiki

;-- M. Hielscher / V.Berger -- (define indent 0) (define-macro (trace-define name expr) `(define ,name (lambda input (set! indent (+ indent 1)) (print (make-string indent #\space) (quote ,name) " " input) (let* ([f ,expr] [r (apply f input)]) (print (make-string indent #\space) r) (set! indent (- indent 1)) r)))) (define listequal? (lambda (ls1 ls2) (cond [(and (null? ls1) (null? ls2)) #t] [(or (null? ls1) (null? ls2)) #f] [(and (list? (car ls1)) (list? (car ls1))) (and (listequal? (car ls1) (car ls2)) (listequal? (cdr ls1) (cdr ls2)))] [else (and (equal? (car ls1) (car ls2)) (listequal? (cdr ls1) (cdr ls2)))])))

Inhaltsverzeichnis 1 Die Fibonaccizahlen 1.1 Aufwandsbetrachtungen 1.2 Experimente 1.3 Endständig rekursive Bestimmung der n-ten Fibonaccizahl 2 Länge einer unverschachtelten bzw. verschachtelten Listen 3 Zählen eines Elements in einer unverschachtelten bzw. verschachtelten Listen 4 Aufgaben 4.1 Elementprüfer 4.2 Streichen eines Elements 4.3 "Glätten" einer verschachtelten Liste 5 Zum Weiterarbeiten 5.1 Superminimum

Die Fibonaccizahlen

Einer der bedeutendsten Mathematiker des Mittelalters, Leonardo Fibonacci di Pisa (* um 1180; † 1241), beschrieb die Fortpflanzung von Kaninchen mit der Zahlenfolge: $1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, ...$ Definition: $\mbox{fibo}(n)=\begin{cases}1,\mbox{wenn}\hspace{0.3em}n=1\\1,\mbox{wenn}\hspace{0.3em}n=2\\\mbox{fibo}(n-1)+\mbox{fibo}(n-2),\mbox{sonst}\end{cases}$ Beschreibung: Die ersten beiden Glieder der Zahlenfolge sind jeweils $1$. Jedes weitere Glied ergibt sich aus der Summe seiner beiden Vorgänger. Das explizite Bildungsvorschrift wurde übrigens unabhängig voneinander von den französischen Mathematikern Abraham de Moivre (* 26. Mai 1667; † 27. November 1754) erst im Jahr 1718 und Jacques Philippe Marie Binet (* 2. Februar 1786; † 12. Mai 1856) sogar erst im Jahr 1843 entdeckt.

Berechnung der "Kaninchenaufgabe" mit der Fibonacci-Folge

Implementation:

(define fibo (lambda (n) (cond [(= n 1) 1] [(= n 2) 1] [else (+ (fibo (- n 1)) (fibo (- n 2)))])))

Hinweis: Testen Sie diese Prozedur mit kleinen Argumenten!

(fibo 6)

ausführen

In dieser echt rekursiven Prozedur erfolgt der rekursive Aufruf zweimal. Rekursionen, in denen der rekursive Aufruf mehrfach erfolgt, heißen Mehrfachrekursionen. Unsere Problemlösungen zum Binärbaum, zu den Fraktalen sowie zum "Turm von Hanoi" sind ebenfalls Mehrfachrekursionen.

Aufwandsbetrachtungen

Mehrfachrekursive Prozeduren können dann sehr uneffizient werden, wenn gleiche Operationen mehrfach ausgeführt werden.
Wir testen dazu die Prozedur im Trace-Modus:

(trace-define fibo (lambda (n) (cond [(= n 1) 1] [(= n 2) 1] [else (+ (fibo (- n 1)) (fibo (- n 2)))])))

(fibo 6)

ausführen

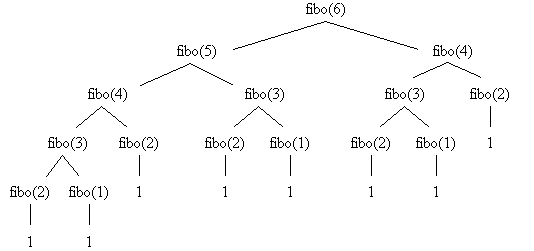
Die nachfolgende Abbildung verdeutlicht die Abarbeitung des Prozeduraufrufs (fibo 6) in einer Baumstruktur:

Die nachfolgende Prozedur berechnet die n-te Fibonaccizahl und bestimmt dabei die Anzahl der Rekursionschritte. Beide Werte werden als Paar (<Ergebnis> . <Aufwand>) ausgegeben:

(define fibo (lambda (n) (cond [(= n 1) 1] [(= n 2) 1] [else (+ (fibo (- n 1)) (fibo (- n 2)))])))

(define fibo-aufwand (lambda (n) (letrec ([aufwand (lambda (n count) (cond [(= n 1) (cons 1 (+ count 1))] [(= n 2) (cons 1 (+ count 1))] [else (let ([f1 (aufwand (- n 1) count)] [f2 (aufwand (- n 2) count)]) (cons (+ (car f1) (car f2)) (+ (cdr f1) 1 (cdr f2))))]))]) (aufwand n 0))))

Hinweis: Während mit let lokale Wertbindungen vorgenommen werden, lassen sich mit letrec lokale rekursive Programmstrukturen definieren.

(fibo-aufwand 6)

ausführen

Experimente

Wir wollen den Aufwand zur Bestimmung der n-ten Fibonaccizahl in einem Balkendiagramm visualisieren. Dazu müssen die Zählergebnisse der Prozedur fibo-aufwand in einer Liste gesammelt werden:

(define experiment (lambda (n schrittweite) (if (< n 1) () (append (experiment (- n schrittweite) schrittweite) (list (cdr (fibo-aufwand n)))))))

(experiment 15 1)

ausführen

Diese Liste wird der Prozedur balkendiagramm mit folgender Syntax übergeben:

(balkendiagramm <ls>) ; <ls> ... Liste mit Zahlenwerten

Achtung! Beim Experimentieren ist etwas Geduld erforderlich!

(define rand 50) (define maxbreite (- 400 (* 2 rand))) (define maxhoehe (- 300 (* 2 rand))) (define minmax (lambda (ls) (letrec ([extremsuche (lambda (extrem ls op) (cond [(null? ls) extrem] [(op extrem (car ls)) (extremsuche (car ls) (cdr ls) op)] [else (extremsuche extrem (cdr ls) op)]))]) (cons (extremsuche 0 ls >) (extremsuche 0 ls <))))) (define balken (lambda (hoehe breite) (forward turtle breite) (left turtle 90) (forward turtle hoehe) (left turtle 90) (forward turtle breite) (left turtle 90) (forward turtle hoehe) (left turtle 90) (forward turtle breite))) (define balkendiagramm (lambda (ls) (let* ([breite (/ maxbreite (length ls))] [extremwerte (minmax ls)] [min (car extremwerte)] [max (cdr extremwerte)]) (letrec ([zeichnen (lambda (min max ls) (if (null? ls) 'ok (begin (balken (floor (* (/ (car ls) (- max min)) maxhoehe)) (floor breite)) (zeichnen min max (cdr ls)))))]) (clear canvas) (hide turtle) (move turtle rand (+ rand (* (/ max (- max min)) maxhoehe))) (right turtle 90) (zeichnen min max ls)))))

(balkendiagramm (experiment 15 1))

ausführen

Endständig rekursive Bestimmung der n-ten Fibonaccizahl

Um den erheblichen Mehraufwand zu vermeiden, könnte sich in diesem Fall eine endständig rekursive Problemlösung (Iteration) anbieten.
Vervollständigen Sie die entsprechende Hilfsprozedur.

(define fibo-it (lambda (n) (fibo-help n 1 1))) (define fibo-help (lambda (n f1 f2) ...))

(fibo-it 100)

ausführen

Es wäre nun falsch anzunehmen, dass Mehrfachrekursionen aus Effizienzgründen vermieden werden müssen. Im Gegenteil!
Mehrfachrekursionen können auch eine universelle Lösungsstrategie spezieller Probleme darstellen.

Länge einer unverschachtelten bzw. verschachtelten Listen

Länge einer unverschachtelten Liste (Anzahl aller Listenelemente):

(define laenge (lambda (ls) (if (null? ls) 0 (+ 1 (laenge (cdr ls))))))

(laenge '(a b c d e f g h i j k l m n))

ausführen

Länge einer verschachtelten Liste:

(define superlaenge (lambda (ls) (cond [(null? ls) 0] [(list? (car ls)) (+ (superlaenge (car ls)) (superlaenge (cdr ls)))] [else (+ 1 (superlaenge (cdr ls)))])))

(superlaenge '(a b (c (d e) (f (g (h i)) j) k l) m n))

ausführen

Zählen eines Elements in einer unverschachtelten bzw. verschachtelten Listen

Elementanzahl in einer unverschachtelten Liste:

(define zaehlen (lambda (el ls) (cond [(null? ls) 0] [(eqv? el (car ls)) (+ 1 (zaehlen el (cdr ls)))] [else (zaehlen el (cdr ls))])))

(zaehlen 'b '(a b s d b c d a b b))

ausführen

Elementanzahl in einer verschachtelten Liste:

(define superzaehlen (lambda (el ls) (cond [(null? ls) 0] [(list? (car ls)) (+ (superzaehlen el (car ls)) (superzaehlen el (cdr ls)))] [(eqv? el (car ls)) (+ 1 (superzaehlen el (cdr ls)))] [else (superzaehlen el (cdr ls))])))

(superzaehlen 'b '(a (b (s (d b)) (c) d a b) b))

ausführen

Hinweis: equal?, eqv? und eq? sind allgemeine Vergleichsprädikate einfacher und höherer Datenstrukturen.

Aufgaben

1. Elementprüfer

   Schreiben Sie zur Wiederholung das Prädikat element?, das entscheidet, ob ein vorgegebenes Element in einer unverschachtelten Liste enthalten ist.

   (define element? (lambda (el ls) ...))

    

   Quelltext überprüfen:

   jetzt prüfen

   (element? 'f '(a b c d e f g h i j))

   ausführen

   Implementieren Sie nun das Prädikat superelement?, das sich in analoger Weise auf verschachtelte Listen anwenden lässt.

   (define superelement? (lambda (el ls) ...))

    

   Quelltext überprüfen:

   jetzt prüfen

   (superelement? 'f '(a b (c (d e (f g)) h i) j))

   ausführen

2. Streichen eines Elements

   Schreiben Sie zunächst nochmals die Prozeduren streiche-erstes und streiche-alle, die ein vorgegebenes Element in einer unverschachtelten Liste beim ersten bzw. bei jedem Auftreten streichen.

   (define streiche-erstes (lambda (el ls) ...))

    

   Quelltext überprüfen:

   jetzt prüfen

   (streiche-erstes 'b '(a b c a b c a b c))

   ausführen

   (define streiche-alle (lambda (el ls) ...))

    

   Quelltext überprüfen:

   jetzt prüfen

   (streiche-alle 'b '(a b c a b c a b c))

   ausführen

   Implementieren Sie nun die Prozeduren superstreichen-erstes bzw. superstreichen-alle für die entsprechenden Anwendungen auf verschachtelte Listen.

   (define superstreichen-erstes (lambda (el ls) ...))

    

   Quelltext überprüfen:

   jetzt prüfen

   (superstreichen-erstes 'b '(a b (c (a (b) c) a) (b) c))

   ausführen

   (define superstreichen-alle (lambda (el ls) ...))

    

   Quelltext überprüfen:

   jetzt prüfen

   (superstreichen-alle 'b '(a b (c (a (b) c) a) (b) c))

   ausführen

3. "Glätten" einer verschachtelten Liste

   Manchmal ist ist es sinnvoll, eine verschachtelte Liste in eine unverschachtelte Liste umzuwandeln. Wir wollen diese Konvertierung als "Glätten" bezeichnen. Dabei muss natürlich jedes Element aus jeder beliebigen Verschachtelungstiefe übernommen werden.
   Implementieren Sie die Prozedur glaetten.

   (define glaetten (lambda (ls) ...))

    

   Quelltext überprüfen:

   jetzt prüfen

   (glaetten '(a b (c (a (b) c) a) (b) c))

   ausführen

Zum Weiterarbeiten

Superminimum

Implementieren Sie das "Superminimum" einer verschachtelten Liste. Entwickeln Sie weitere Prozeduren für verschachtelte Listen.

Zur Problemlösung.