Fraktale

Aus ProgrammingWiki

< Grundlagen der funktionsorientierten Programmierung mit SCHEME

Die vielleicht berühmteste fraktale Struktur: Das Apfelmännchen

Der Begriff Fraktal (lat. fractus "gebrochen") geht auf den französisch-US-amerikanischen Mathematiker Benoît Mandelbrot (* 20. November 1924; † 14. Oktober 2010) zurück. Mit ihm werden natürliche oder künstliche Gebilde bzw. geometrische Muster bezeichnet, die einen hohen Grad an Selbstähnlichkeiten aufweisen.

Hinweis: Zur Implementation fraktaler Figuren stehen Ihnen auch hier die Sprachelemente der Turtle-Grafik zur Verfügung.

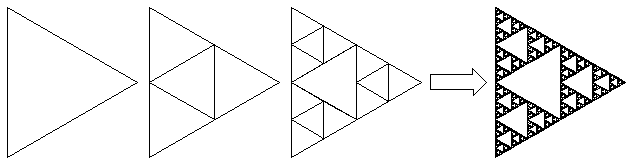
Das Sierpinski-Dreieck

Diese selbstähnliche Figur ist nach dem polnischen Mathematiker Wacław Franciszek Sierpiński (* 14. März 1882; † 21. Oktober 1969) benannt. Die nachfolgende Abbildung zeigt die Konstruktion dieses Dreiecks:

Implementation:

(define dreieck (lambda (turtle len) ...)) (define sierpinski (lambda (turtle len n) (if (= n 1) (dreieck turtle len) (begin ...)))) (define sierpinski-dreieck (lambda (len n) (clear canvas1) (move turtle1 100 300) ...))

(sierpinski-dreieck 300 6)

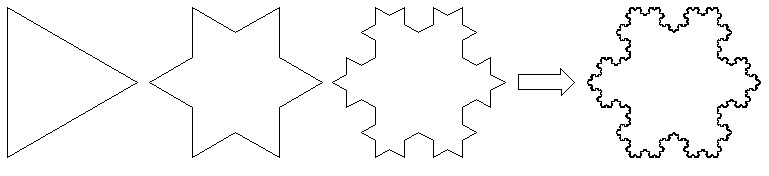
Die Koch-Schneeflocke

Der schwedische Mathematiker Helge von Koch (* 25. Januar 1870; † 11. März 1924) stellte im Jahr 1904 einen stetigen Graphen vor, der an keiner Stelle differenzierbar ist. Die sogenannte Koch-Schneeflocke setzt sich aus drei dieser Koch-Kurven zusammen, die auf den Seiten eines gleichseitigen Dreiecks angeordnet sind:

Implementation:

(define koch (lambda (turtle len n) (if (= n 1) (forward turtle len) (begin ...)))) (define koch-schneeflocke (lambda (len n) (clear canvas2) (move turtle2 150 270) ...))

(koch-schneeflocke 300 6)

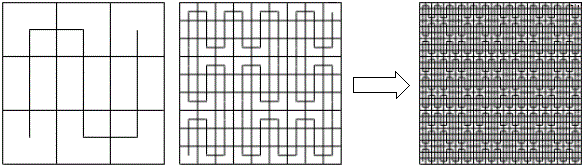
Die Peano-Kurve

Der italienische Mathematiker Giuseppe Peano (* 27. August 1858; † 20. April 1932) konstruierte eine raumfüllende Kurve, die mit zunehmender Rekursionstiefe punktweise konvergiert. Damit kann mit einer eindimensionalen Kurve eine zweidimensionale Fläche und sogar ein dreidimensionaler Raum vollständig ausgefüllt werden.

Implementation:

(define black (lambda (turtle) (pencolor turtle 0 0 0))) (define red (lambda (turtle) (pencolor turtle 255 0 0))) (define brown (lambda (turtle) (pencolor turtle 100 50 0))) (define orange (lambda (turtle) (pencolor turtle 255 100 0))) (define yellow (lambda (turtle) (pencolor turtle 255 200 0))) (define green (lambda (turtle) (pencolor turtle 0 255 0))) (define blue (lambda (turtle) (pencolor turtle 0 0 255))) (define pink (lambda (turtle) (pencolor turtle 200 50 200))) (define raster (lambda (turtle len n color) (letrec ([rechteck (lambda (m) (if (> m 0) (begin (forward turtle len) (right turtle 90) (forward turtle (/ len 2 n)) (right turtle 90) (forward turtle len) (left turtle 90) (forward turtle (/ len 2 n)) (left turtle 90) (rechteck (- m 1))) (begin (left turtle 90) (penerase turtle) (forward turtle (/ len 2 n)) (color turtle) (right turtle 90))))]) (rechteck n) (left turtle 90) (forward turtle len) (right turtle 90) (forward turtle len) (right turtle 90) (rechteck n) (left turtle 90))))

(define kurve (lambda (turtle vz len) ...)) (define peano (lambda (turtle vz len n) (if (= n 1) (kurve turtle vz len) (begin ...)))) (define peano-kurve (lambda (len n) (let ([dl (/ (* len (- 1 (/ 1 (expt 3 n)))) 2)]) (clear canvas3) (move turtle3 (- 190 (/ len 2)) (+ 200 (/ len 2))) (red turtle3) (raster turtle3 len (/ (expt 3 n) 2) red) (move turtle3 (- 190 dl) (+ 200 dl)) (black turtle3) ...)))

(peano-kurve 300 3)

Zurück zu Rekursionen.

Fraktale

Aus ProgrammingWiki

Das Sierpinski-Dreieck

Die Koch-Schneeflocke

Die Peano-Kurve

Ansichten

Persönliche Werkzeuge

Navigation

Suche

Werkzeuge