Rekursionen

Aus ProgrammingWiki

(define sqr (lambda (x) (* x x))) (define pi (* 4 (atan 1))) (define eps 1e-03) (define runden (lambda (x anzahl) (/ (round (* x (expt 10 anzahl))) (expt 10 anzahl)))) (define grenzwert (lambda (r) (* (/ 1 2) (+ (sqrt 5) 1) r))) (define char-downcase (lambda (z) (let ([nr (char->integer z)]) (if (and (> nr 64) (< nr 91)) (integer->char (+ nr 32)) z)))) (define char-upcase (lambda (z) (let ([nr (char->integer z)]) (if (and (> nr 96) (< nr 123)) (integer->char (- nr 32)) z))))

Inhaltsverzeichnis 1 Abgestützte Prozeduren 2 Selbstähnlichkeiten 2.1 Der Binärbaum 2.2 Die "Quadratschnecke" 3 Rekursive Fakultätsfunktion 4 Das Affenmodell 5 Aufgaben 5.1 Summe natürlicher Zahlen 5.2 Summe ganzer Zahlen 5.3 Vokalzähler 5.4 Teilzeichenketten 5.5 Widerstandsnetzwerk 6 Zum Weiterarbeiten 6.1 Fraktale

Abgestützte Prozeduren

Wir wissen: Neue Objekte können mit bereits definierten Prozeduren beschrieben werden.

Beispiel: Volumen eines geraden Kreiszylinders:

(define kreisflaeche (lambda (r) (* pi (sqr r)))) (define zylindervolumen (lambda (r h) (* (kreisflaeche r) h))) (zylindervolumen 5.5 12) ausführen

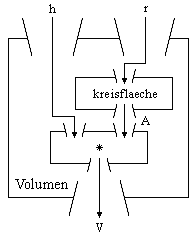Man sagt: Die Definition von zylindervolumen wird auf der Definition von kreisflaeche abgestützt.
Wie sinnvoll ist es, Prozeduren auf sich selbst abzustützen?

Selbstähnlichkeiten

Der Binärbaum

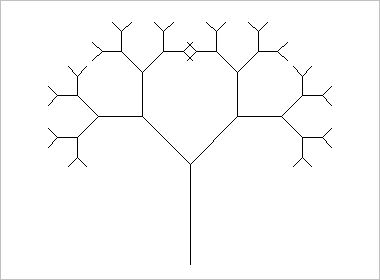
Zunächst betrachten wir das nachfolgende Grafikobjekt, das wir als Binärbaum bezeichnen wollen. Dabei fällt auf, dass jeder Ast wieder ein kleiner Binärbaum ist.
Wir wollen diese Selbstähnlichkeit zu seiner Beschreibung ausnutzen:

Beschreibung: Der einfachste Binärbaum besteht aus einem Stamm. Jeder andere Binärbaum besteht aus einem Stamm sowie einem vereinfachten linken und einem vereinfachten rechten Binärbaum.

Wir stellen fest, dass es durchaus sinnvoll sein kann, Objekte mit sich selbst zu beschreiben.
Mit der Turtle-Grafik wollen wir eine gleichwertige Implementation vornehmen. Dazu definieren wir den Baum mit sich selbst.

Hinweis: Hier finden Sie die Sprachelemente der Turtle-Grafik.

(define baum (lambda (turtle len n) (if (> n 0) (begin (forward turtle len) (left turtle 45) (baum turtle (* (/ 2 3) len) (- n 1)) (right turtle 90) (baum turtle (* (/ 2 3) len) (- n 1)) (left turtle 45) (backward turtle len)) 'ok))) (define binaerbaum (lambda (len n) (clear canvas1) (move turtle1 200 300) (baum turtle1 len n))) (binaerbaum 100 6) ausführen

Die "Quadratschnecke"

Beschreibung:

• Die einfachste Quadratschnecke besteht aus einer Strecke.
• Jede andere Quadratschnecke besteht aus einer Strecke, einer Drehung um 90° sowie einer etwas verkürzten Quadratschnecke.

(define schnecke (lambda (turtle len) (if (> len 0) (begin (forward turtle len) (right turtle 90) (schnecke turtle (- len 2))) 'ok))) (define quadschnecke (lambda (len) (clear canvas2) (move turtle2 90 290) (schnecke turtle2 len))) (quadschnecke 200) ausführen

Prozeduren, die mit sich selbst definiert werden, heißen rekursive¹⁾ Prozeduren.
Rekursionen stellen ein leistungsstarkes und universelles Konzept zur Problemlösung dar.

¹⁾ recurrere (lat.): "zurücklaufen"

Rekursive Fakultätsfunktion

Nun analysieren wir die mathematische Definition der Fakultätsfunktion:

$n!=\prod\limits_{i=1}^{n}i=1 \cdot 2 \cdot 3 \cdot ... \cdot n$

bzw. rekursiv:

$n!=\begin{cases}1,\mbox{wenn}\hspace{0.3em}n=0\\n \cdot (n-1)!\end{cases}$

Auch hier ist die Definition mit sich selbst offensichtlich.

Beschreibung:

• Die Fakultät einer Zahl ist 1, wenn die Zahl 0 ist,
• anderenfalls berechnet sie sich aus dem Produkt dieser Zahl mit der Fakultät ihres Vorgängers.

Implementation:

(define fak (lambda (n) (if (= n 0) 1 (* n (fak (- n 1)))))) (fak 4) ausführen

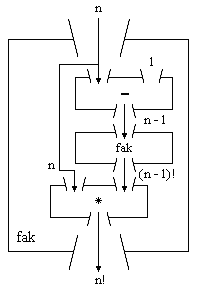Beachte: Rekursive Prozeduren enthalten neben dem rekursiven Prozeduraufruf immer eine Elementarbedingung!

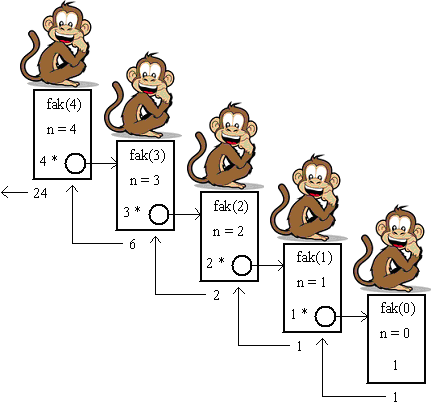
Das Affenmodell

Eine schöne Interpretation des rekursiven Prozeduraufrufes finden wir bei WAGENKNECHT in [8], S. 42:

"Der Auftrag, der von außen dem höchsten Oberaffen übergeben wurde, wird von diesem nicht vollständig bearbeitet, sondern in etwas abgeschwächter Form dem untergebenen Affen übergeben. Dieser verhält sich ebenso zu seinem Untergebenen. Der letzte Affe in dieser Hierarchie kann den ihm übergebenen Auftrag erfüllen und dem übergeordneten Affen übergeben. Jeder weitere Affe hat die Pflicht, das Resultat der Erledigung seines Auftrages seinem Auftraggeber zu übergeben. Schließlich kann der Ranghöchste sein Ergebnis abliefern.
Parallelen zu Einrichtungen, Ämtern und Institutionen unserer Gesellschaft sind unbeabsichtigt oder rein zufällig."

Aufgaben

(define test-summe (lambda (n) (if (= n 0) 0 (+ (test-summe (- n 1)) n)))) (define test-summe-von-bis (lambda (von bis) (if (= von bis) von (+ bis (test-summe-von-bis von (- bis 1))))))

1. Summe natürlicher Zahlen

   Ermitteln Sie die Summe einer beliebigen Anzahl natürlicher Zahlen: $S=\sum\limits_{i=0}^{n}i=1 + 2 + 3 + ... + n$.
   Im Gegensatz zu Carl Friedrich Gauß (* 30. April 1777; † 23. Februar 1855; deutscher Mathematiker, Astronom und Physiker) soll (noch) keine Summenformel benutzt werden!

   • Beschreiben Sie die rekursive Definition einer Summenfunktion.
   • Skizzieren Sie das entsprechende Trichtermodell.
   • Implementieren Sie die Summenfunktion summe als rekursive Prozedur.

   (define summe (lambda (n) ...))

    

   Quelltext überprüfen:

   jetzt prüfen

   (summe 100)

   ausführen

2. Summe ganzer Zahlen

   Schreiben Sie nun eine Prozedur summe-von-bis, die die Summe ganzer Zahlen in einem abgeschlossenen Intervall bildet.

   (define summe-von-bis (lambda (von bis) ...))

    

   Quelltext überprüfen:

   jetzt prüfen

   (summe-von-bis -99 100)

   ausführen

   Überprüfen Sie das Prozedurergebnis mit einer Hilfsprozedur, die eine Summenformel ganzer Zahlen nutzt (Herleitung!).

   (define berechne-von-bis (lambda (von bis) ...))

    

   Quelltext überprüfen:

   jetzt prüfen

   (berechne-von-bis -99 100)

   ausführen

3. Vokalzähler

   In einer Zeichenkette sollen alle Vokale unabhängig von ihrer Groß- oder Kleinschreibung gezählt werden.
   Vervollständigen Sie die entsprechende Prozedur.

   (define vokalzaehler (lambda (zk) ...))

    

   Quelltext überprüfen:

   jetzt prüfen

   (vokalzaehler "Amadeus")

   ausführen

4. Teilzeichenketten

   In Datenbanksystemen gehört die Suche nach Teilen einer Zeichenkette zur Standardfunktionalität.
   Implementieren Sie das Prädikat (substring? <zk1> <zk2>), das entscheiden soll, ob die Zeichenkette zk1 in der Zeichenkette zk2 enthalten ist.

   Hinweis:

   Zum Vergleich von Zeichenketten wird der Vergleichsoperator equal? benötigt. Weitere Informationen zu Vergleichsoperatoren findet man hier.

   (define substring? (lambda (zk1 zk2) ...))

    

   Quelltext überprüfen:

   jetzt prüfen

   (substring? "form" "Informatik")

   ausführen

5. Widerstandsnetzwerk

   Zunächst besteht eine einfache elektrische Grundschaltung aus 2 gleichgroßen Widerständen. Durch Anhängen weiterer dieser Grundschaltungen entsteht daraus ein komplexes Widerstandsnetzwerk:

   

   
   

   Entwickeln Sie eine Prozedur, die den Gesamtwiderstand zwischen den Anschlussklemmen $A$ und $B$ berechnet, wenn $n$ Grundschaltungen zu diesem Widerstandsnetzwerk zusammengesetzt wurden.

   (define widerstand (lambda (r n) ...))

    

   Quelltext überprüfen:

   jetzt prüfen

   (widerstand 100 10)

   ausführen

   ZA: Grenzwert des Gesamtwiderstandes

   Zeigen Sie, dass mit $n \rightarrow \infty$ für den Grenzwert des Gesamtwiderstandes dieses Widerstandsnetzwerkes gilt:

   $R_{Ges} = \frac{\sqrt{5}+1}{2} R$

   Überprüfen Sie die obige Widerstandsberechnung mit der Berechnung dieses Grenzwertes:

   (define widerstand-grenzwert (lambda (r) ...))

   (widerstand-grenzwert 100)

   ausführen

Zum Weiterarbeiten

Fraktale

Mit selbstähnlichen Figuren bzw. Objekten beschäftigt sich heute ein ganzes Teilgebiet der Mathematik, die fraktale Geometrie. Ihre Untersuchungsergebnisse reichen in die Funktions- und Berechnbarkeitstheorie hinein und haben einen wesentlichen Einfluss auf die Chaosforschung komplexer dynamischer Systeme.
Klassische selbstähnliche oder fraktale Figuren sind das Sierpinski-Dreieck, die Koch-Schneeflocke und die Peano-Kurve:

Beschreiben Sie die drei Fraktale verbal und implementieren Sie diese mit der Turtle-Grafik.

Zur Problemlösung.