Komplexe Anwendungen: Numerische Listen

Aus ProgrammingWiki

Inhaltsverzeichnis 1 Einführung 1.1 Letztes Listenelement 2 Aufgaben 2.1 Länge einer Liste 2.2 Elementprüfer 2.3 Zählen eines Listenelements 2.4 n-tes Listenelement 2.5 Zufallselement 2.6 Listenelement an n-ter Stelle einfügen 2.7 Listenelement an n-ter Stelle streichen 2.8 Streichen eines Listenelements beim ersten Auftreten 2.9 Streichen eines Listenelements bei jedem Auftreten 2.10 Kleinstes Listenelement 2.11 Häufigstes Listenelement 2.12 ZA: Schnapszahlen 3 Zum Weiterarbeiten 3.1 Vergleichsoperatoren 3.2 Minimum-Sortieren

Einführung

Wir wollen ausgewählte Prozeduren erstellen, die auf numerische Listen anzuwenden sind. Die Elemente dieser Listen sollen ausschließlich ganze Zahlen sein.

Beispiel:

(define numliste '(2 3 5 -1 3 6 11 18 15 0 19 27 -33 -2 55 31 7 39 22 1))

Zu allen Aufgaben sind, sofern nicht anders formuliert,

• eine verbale Beschreibung,
• das vereinfachte Trichtermodell sowie
• die vollständige Implementation

anzugeben.

Als Musterlösung soll das letzte Element einer numerischen Liste ermittelt werden:

Letztes Listenelement

Beschreibung:

Das letzte Element ist

• das erste Listenelement, wenn die Liste einelementig ist oder
• das letzte Element der Restliste.

Hinweis: Unter der Restliste wollen wir stets die Liste ohne das erste Listenelement verstehen.

Trichtermodell:		Implementation:
		(define letztes (lambda (ls) (if (null? (cdr ls)) (car ls) (letztes (cdr ls))))) (letztes numliste) ausführen

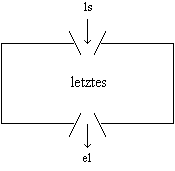Aufgaben

(define my-element? (lambda (el ls) (cond [(null? ls) #f] [(= el (car ls)) #t] [else (my-element? el (cdr ls))]))) (define quotient (lambda (m n) (floor (/ m n)))) (define remainder quotient) (define listequal? (lambda (ls1 ls2) (cond [(and (null? ls1) (null? ls2)) #t] [(or (null? ls1) (null? ls2)) #f] [(and (list? (car ls1)) (list? (car ls1))) (and (listequal? (car ls1) (car ls2)) (listequal? (cdr ls1) (cdr ls2)))] [else (and (equal? (car ls1) (car ls2)) (listequal? (cdr ls1) (cdr ls2)))])))

1. Länge einer Liste

   Es soll die Länge einer Liste, d.h. die Anzahl aller Listenelemente bestimmt werden.

   (define laenge (lambda (ls) ...))

    

   Quelltext überprüfen:

   jetzt prüfen

   (laenge numliste)

   ausführen

2. Elementprüfer

   Mit einem Prädikat soll geprüft werden, ob ein vorgegebenes Element in einer Liste enthalten ist.

   (define element? (lambda (el ls) ...))

    

   Quelltext überprüfen:

   jetzt prüfen

   (element? 19 numliste)

   ausführen

3. Zählen eines Listenelements

   In einer Liste soll die Häufigkeit ermittelt werden, mit der ein ausgewähltes Listenelement vorkommt.

   (define anzahl (lambda (el ls) ...))

    

   Quelltext überprüfen:

   jetzt prüfen

   (anzahl 3 numliste)

   ausführen

4. n-tes Listenelement

   Die Selektoren car und cdr können nur beschränkt zur Elementauswahl in beliebig langen numerischen Listen herangezogen werden. Deshalb soll eine Prozedur dabei helfen, das n-te Listenelement zurückzugeben.

   Beispiel:

   (n-tes '(2 3 5 -1 3 6 11 18 15 0 19 27 -33 -2 55 31 7 39 22 1) 17)
   --> 7

   (define n-tes (lambda (ls n) ...))

    

   Quelltext überprüfen:

   jetzt prüfen

   (n-tes numliste 17)

   ausführen

5. Zufallselement

   Ermitteln Sie mit der Prozedur n-tes ein zufälliges Element aus einer nichtleeren numerischen Liste. Benutzen Sie dazu die bereits bekannte Prozedur (random <max>) mit $0 \le z < max$.

   (define zufallselement (lambda (ls) ...))

    

   Quelltext überprüfen:

   jetzt prüfen

   (zufallselement numliste)

   ausführen

6. Listenelement an n-ter Stelle einfügen

   Natürlich muss es auch möglich sein, ein Element an einer beliebigen Stelle in eine Liste einzufügen. Vervollständigen Sie die entsprechende Prozedur. Achten Sie darauf , dass das Element ggf. an letzter Stelle angefügt wird, falls die gewünschte Position die Listenlänge überschreitet.

   Beispiele:

   (n-tes-einfuegen 100 '(2 3 5 -1 3 6 11 18 15 0 19 27 -33 -2 55 31 7 39 22 1) 3)
   --> (2 3 100 5 -1 3 6 11 18 15 0 19 27 -33 -2 55 31 7 39 22 1)
   
   (n-tes-einfuegen 100 '(2 3 5 -1 3 6 11 18 15 0 19 27 -33 -2 55 31 7 39 22 1) 433)
   --> (2 3 5 -1 3 6 11 18 15 0 19 27 -33 -2 55 31 7 39 22 1 100)

   (define n-tes-einfuegen (lambda (el ls n) ...))

    

   Quelltext überprüfen:

   jetzt prüfen

   (n-tes-einfuegen 100 numliste 3)

   ausführen

7. Listenelement an n-ter Stelle streichen

   In Umkehrung der letzten Prozedur soll nun ein Element an einer beliebigen Stelle gestrichen werden. Ergänzen Sie die entsprechende Prozedur n-tes-streichen. Falls hier die gewünschte Position die Listenlänge überschreitet, ist die Liste unverändert zurückzugeben.

   Beispiele:

   (n-tes-streichen '(2 3 5 -1 3 6 11 18 15 0 19 27 -33 -2 55 31 7 39 22 1) 3)
   --> (2 3 -1 3 6 11 18 15 0 19 27 -33 -2 55 31 7 39 22 1)
   
   (n-tes-streichen '(2 3 5 -1 3 6 11 18 15 0 19 27 -33 -2 55 31 7 39 22 1) 433)
   --> (2 3 5 -1 3 6 11 18 15 0 19 27 -33 -2 55 31 7 39 22 1)

   (define n-tes-streichen (lambda (ls n) ...))

    

   Quelltext überprüfen:

   jetzt prüfen

   (n-tes-streichen numliste 3)

   ausführen

8. Streichen eines Listenelements beim ersten Auftreten

   Ein Listenelement soll bei seinem ersten Auftreten gestrichen werden. Jedes weitere Auftreten dieses Elements bleibt unberücksichtigt.

   Beispiel:

   (streiche-erstes 3 '(2 3 5 -1 3 6 11 18 15 0 19 27 -33 -2 55 31 7 39 22 1))
   --> (2 5 -1 3 6 11 18 15 0 19 27 -33 -2 55 31 7 39 22 1)

   (define streiche-erstes (lambda (el ls) ...))

    

   Quelltext überprüfen:

   jetzt prüfen

   (streiche-erstes 3 numliste)

   ausführen

9. Streichen eines Listenelements bei jedem Auftreten

   Nun soll ein Listenelement bei jedem Auftreten gestrichen werden.

   Beispiel:

   (streiche-alle 3 '(2 3 5 -1 3 6 11 18 15 0 19 27 -33 -2 55 31 7 39 22 1))
   --> (2 5 -1 6 11 18 15 0 19 27 -33 -2 55 31 7 39 22 1)

   (define streiche-alle (lambda (el ls) ...))

    

   Quelltext überprüfen:

   jetzt prüfen

   (streiche-alle 3 numliste)

   ausführen

10. Kleinstes Listenelement

    Mit einem geeigneten Suchalgorithmus soll das kleinste Element einer numerischen Liste ermittelt werden.

    Beispiel:

    (minimum '(2 3 5 -1 3 6 11 18 15 0 19 27 -33 -2 55 31 7 39 22 1))
    --> -33

    (define minimum (lambda (ls) ...))

     

    Quelltext überprüfen:

    jetzt prüfen

    (minimum numliste)

    ausführen

11. Häufigstes Listenelement

    Im Gegensatz zur Aufgabe 3 soll nun das Listenelement ermittelt werden, das am häufigsten auftritt. Trifft das auf mehrere Listenelemente zu, so ist nur eins dieser Elemente auszugeben.

    Beispiele:

    (maxelement '(2 3 5 -1 3 6 11 18 15 0 19 27 -33 -2 55 31 7 39 22 1))
    --> 3
    (maxelement '(2 3 5 -1 3 5 1 5 3))
    --> 3 oder 5
    

    Hinweis: Die Prozedur anzahl aus Aufgabe 3 eignet sich zur Problemlösung als Hilfsprozedur.

    (define maxelement (lambda (ls) ...))

     

    Quelltext überprüfen:

    jetzt prüfen

    (maxelement numliste)

    ausführen

12. ZA: Schnapszahlen

    Aus einer vorgegebenen numerischen Liste sollen alle Schnapszahlen herausgesucht werden.

    Beispiel:

    (schnapszahlen '(2 3 5 -1 3 6 11 18 15 0 19 27 -33 -2 55 31 7 39 22 1))
    --> (11 55 22)

    Zunächst sollten wir uns klarmachen, was wir unter einer Schnapszahl verstehen wollen:

    Beschreibung:

    • Eine einstellige oder negative Zahl ist keine Schnapszahl.
    • Eine zweistellige Zahl ist eine Schnapszahl, wenn beide Ziffern gleich sind.
    • Eine mehrstellige Zahl ist eine Schnapszahl, wenn ihre letzten beiden Ziffern gleich sind und die Zahl ohne die letzte Ziffer eine Schnapszahl ist.

    Es empfiehlt sich, ein separates Prädikat zur Schnapszahlprüfung zu implementieren.
    

    Hinweise:

    • Mit der Prozedur quotient kann eine ganzzahlige Division ohne Rest ausgeführt werden:

      (quotient 35 10) --> 3
      (quotient 7 10)  --> 0

    • Mit der Prozedur modulo kann der Rest einer ganzzahlige Division ermittelt werden:

      (modulo 35 10) --> 5
      (modulo 7 10)  --> 7

    Implementation:

    (define schnapszahl? (lambda (n) ...)) (define schnapszahlen (lambda (ls) ...))

     

    Quelltext überprüfen:

    jetzt prüfen

    (schnapszahlen numliste)

    ausführen

Zum Weiterarbeiten

Vergleichsoperatoren

Wir haben bereits die Syntax der Vergleichsoperatoren einfacher Datentypen kennen gelernt. Wie lassen sich nun Daten komplexerer Datenstrukturen vergleichen?
Eine Übersicht der darauf anzuwendenden Vergleichsoperatoren equal?, eqv?, eq? finden Sie hier.

Minimum-Sortieren

Mit den Prozeduren streiche-erstes und minimum ist es möglich, einen ersten Sortieralgorithmus zu beschreiben, den wir als Minimum-Sortieren oder kurz als MinSort bezeichnen wollen:

Beschreibung:

• Suche aus einer numerischen Liste das Minimum heraus,
• streiche es an seiner ursprünglichen Stelle und
• stelle es der Minimum-sortierten Restliste voran.

Implementieren Sie diesen Algorithmus.

Zur Problemlösung.