MinSort

Aus ProgrammingWiki

(define listequal? (lambda (ls1 ls2) (cond [(and (null? ls1) (null? ls2)) #t] [(or (null? ls1) (null? ls2)) #f] [(and (list? (car ls1)) (list? (car ls1))) (and (listequal? (car ls1) (car ls2)) (listequal? (cdr ls1) (cdr ls2)))] [else (and (equal? (car ls1) (car ls2)) (listequal? (cdr ls1) (cdr ls2)))]))) (define rand 50) (define maxbreite (- 400 (* 2 rand))) (define maxhoehe (- 300 (* 2 rand))) (define minmax (lambda (ls) (letrec ([extremsuche (lambda (extrem ls op) (cond [(null? ls) extrem] [(op extrem (car ls)) (extremsuche (car ls) (cdr ls) op)] [else (extremsuche extrem (cdr ls) op)]))]) (cons (extremsuche 0 ls >) (extremsuche 0 ls <))))) (define balken (lambda (hoehe breite turtle) (forward turtle breite) (left turtle 90) (forward turtle hoehe) (left turtle 90) (forward turtle breite) (left turtle 90) (forward turtle hoehe) (left turtle 90) (forward turtle breite))) (define balkendiagramm (lambda (ls nr) (let* ([breite (/ maxbreite (length ls))] [extremwerte (minmax ls)] [min (car extremwerte)] [max (cdr extremwerte)] [canvas (eval (string->symbol (string-append "canvas" (number->string nr))))] [turtle (eval (string->symbol (string-append "turtle" (number->string nr))))]) (letrec ([zeichnen (lambda (min max ls) (if (null? ls) 'ok (begin (balken (floor (* (/ (car ls) (- max min)) maxhoehe)) (floor breite) turtle) (zeichnen min max (cdr ls)))))]) (clear canvas) (hide turtle) (move turtle rand (+ rand (* (/ max (- max min)) maxhoehe))) (right turtle 90) (zeichnen min max ls)))))

Inhaltsverzeichnis 1 Algorithmus 2 Effizienz von MinSort 2.1 Theoretische Analyse des Zeitaufwands 2.2 Experimente zum Zeitaufwand 3 Aufgaben 4 Zum Weiterarbeiten 4.1 GnomeSort

Algorithmus

Bei einfachen rekursiven Problemlösungen haben wir Algorithmen implementiert, die der Suche des Minimums bzw. dem Streichen eines Elements in unverschachtelten numerischen Listen entsprechen. Daraus haben wir bereits einen ersten Sortieralgorithmus konstruiert:

Beschreibung:

• Suche aus der Liste das Minimum heraus,
• streiche es an seiner ursprünglichen Stelle und
• stelle es der Minimum-sortierten Restliste voran.

Da sich dieser Algorithmus am Minimum einer Liste orientiert, bezeichnen wir ihn als MinSort. Auf diese Weise sortieren Kartenspieler recht häufig ihre Spielkarten in der Hand.
Implementieren Sie den Algorithmus und testen Sie ihn an Listen mit Zufallszahlen $z$, mit $z \in \mathbb{Z}$.
Stellen Sie dazu die ungeordnete und die geordnete Zahlenliste jeweils in einem Balkendiagramm grafisch dar.

(define zufallszahl (lambda (min max) (+ (random (- max min -1)) min))) (define zufallsliste (lambda (min max anzahl) (if (= anzahl 0) () (cons (zufallszahl min max) (zufallsliste min max (- anzahl 1)))))) ;Minimum einer Liste (define minimum (lambda (ls) ...)) ;Streichen eines Listenelements beim ersten Auftreten (define streichen (lambda (el ls) ...)) ;Minsort (define minsort (lambda (ls) ...))

Ungeordnete Zufallszahlen:

Geordnete Zufallszahlen:

(define ls (zufallsliste 1 1000 100)) (balkendiagramm ls 1) (define ls-sort (minsort ls)) (balkendiagramm ls-sort 2)

ausführen

Hinweis: Um mehrere Zeichenflächen nutzen zu können, muss die Prozedur balkendiagramm mit einem zusätzlichen Parameter ausgestattet werden, der einer fortlaufenden Nummerierung entspricht:

(balkendiagramm
  <ls>       ; Liste mit Zahlenwerten   
  <nr>)      ; fortlaufende Nummerierung des Balkendiagramms

Effizienz von MinSort

Theoretische Analyse des Zeitaufwands

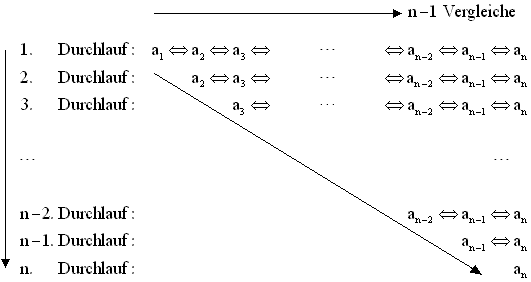
Wir überlegen uns zunächst, wie viele Vergleiche bei der Minimumsuche insgesamt durchgeführt werden:

Das Schema lässt sich mit einer Dreieckfläche vergleichen. Damit sind also $\tfrac{n}{2} (n-1)$ Vergleiche zum Auffinden des Minimums notwendig.
Zum Streichen des gefundenen Minimums sind ähnliche Überlegungen möglich. Im Mittel kann man aber davon ausgehen, dass das Streichen nach $\tfrac{n}{2}$ Vergleichen pro Durchlauf abgeschlossen ist (endständig rekursive Prozedur).
Damit ist folgende Abschätzung für den Gesamtaufwand möglich:

$T(n) = \underbrace{\frac{n}{2} \cdot (n-1)}_{Min-Suche} + \underbrace{\frac{1}{2} \cdot \frac{n}{2} \cdot (n-1)}_{Streichen} = \frac{3}{4} \cdot n \cdot (n-1)$

$T(n) \approx \frac{3}{4} \cdot n^2$   bzw.

$T(n) = \mathcal{O}(n^2)$

Das Minimum-Sortieren erfolgt mit quadratischem Zeitaufwand.

Experimente zum Zeitaufwand

Wir wollen unsere theoretische Analyse empirisch bestätigen. Dazu definieren wir unseren MinSort-Algorithmus mit einem "eingebauten" (Zeittakt-)Zähler:

(define count 0) (define minsort-aufwand (lambda (ls) (letrec ([minsuche (lambda (ls) (cond [(null? (cdr ls)) (car ls)] [(< (car ls) (cadr ls)) (set! count (+ 1 count)) ;Extremwertsuche mit neuem Element (minsuche (cons (car ls) (cddr ls)))] [else (set! count (+ 1 count)) ;Extremwertsuche mit altem Element (minsuche (cdr ls))]))] [streiche (lambda (el ls) (cond [(null? ls) ()] [(eqv? el (car ls)) (set! count (+ 1 count)) ;Streichen (cdr ls)] [else (set! count (+ 1 count)) ;Suche zum Streichen (cons (car ls) (streiche el (cdr ls)))]))]) (if (null? ls) () (let ([el (minsuche ls)]) (cons el (minsort-aufwand (streiche el ls)))))))) (define minsort-ausgabe (lambda (min max anzahl) (let ([ls (zufallsliste min max anzahl)]) (set! count 0) (display "Ungeordnete Zufallszahlen:") (display ls) (display "Geordnete Zufallszahlen:") (display (minsort-aufwand ls)) (display "Anzahl der Minimumvergleiche und Streichungen: " (number->string count)) 'ok)))

(minsort-ausgabe 1 1000 20)

ausführen

Im Weiteren wollen wir uns wieder nur auf die Zählergebnisse unseres "Zeittaktmessers" konzentrieren.
Dazu sollen die Wiederholungen des Experimentes automatisiert werden:

(define minsort-mehrfach (lambda (min max anzahl whlg) (letrec ([summe (lambda (n) (if (= n 0) 0 (begin (set! count 0) (minsort-aufwand (zufallsliste min max anzahl)) (+ count (summe (- n 1))))))]) (/ (summe whlg) whlg))))

(minsort-mehrfach 1 1000 20 10)

ausführen

Schließlich sollen die Ergebnisse unserer empirischen Untersuchung wieder im Balkendiagramm visualisiert werden.

(define experiment (lambda (min max anzahl schrittweite whlg) (if (< anzahl 1) () (append (experiment min max (- anzahl schrittweite) schrittweite whlg) (list (minsort-mehrfach min max anzahl whlg))))))

Achtung! Mit kleinen Wiederholraten und etwas Geduld experimentieren!

(balkendiagramm (experiment 1 1000 20 1 10) 3)

ausführen

Die empirischen Untersuchungen bestätigen den quadratischen Zeitaufwand von MinSort.

Aufgaben

1. Ermitteln Sie mit der Prozedur minsort-mehrfach empirisch die Zeitaufwandsfunktion $T:\mathbb{N} \rightarrow \mathbb{R}^+$.
   Nutzen Sie dazu eine Tabellenkalkulation oder den grafikfähigen Taschenrechner. Bestimmen Sie die Funktionsgleichung $T(n) = f(n)$ durch quadratische Regression und vergleichen Sie diese mit den oben angeführten theoretischen Überlegungen.
2. Implementieren Sie unter DrScheme den MinSort-Algorithmus zum lexikografischen Ordnen von Zeichenketten.
   Dabei soll wahlweise aufsteigend oder absteigend geordnet werden können (Prozeduren höherer Ordnung!).

Zum Weiterarbeiten

GnomeSort

In einem Garten sind Blumentöpfe in einer Reihe aufgestellt. Gartenzwerge sollen sie nun der Größe nach aufsteigend sortieren. Sie benutzen dazu den folgenden Algorithmus:

• Beginne links und vergleiche die beiden ersten Töpfe.
• Stehen sie in der richtigen Reihenfolge gehe ein Schritt nach rechts.
• Wenn sie nicht in der korrekten Reihenfolge stehen, vertausche die beiden Töpfe und gehe einen Schritt nach links.
  Ist der Schritt nach links nicht möglich, gehe ein Schritt nach rechts.
• Wiederhole das Sortieren bis zum letzten Blumentopf.

Implementieren Sie diesen Algorithmus und untersuchen Sie seine Effizienz im average- best- und worst-case-Fall.

Zur Problemlösung.