Dynamic Programming
Aus ProgrammingWiki
Dynamic Programming (dynamisches Programmieren; DP) kann Effizienzverbesserungen erzielen, indem wiederkehrende Teilprobleme (vorsorglich) gelöst werden. Das Wort Programming steht hier für Optimierung (ähnlich wie bei Linear Programming). Optimierung ist zutreffend, da mit Dynamic Progamming Optimierungsprobleme gelöst werden, also Probleme, bei denen ein Minimum bzw. Maximum gefunden werden soll. Die Methode wurde von Richard Ernest Bellman (29.08.1920-19.03.1984) im Jahre 1940 zur Lösung von Problemen in der Regelungstechnik angewandt.
Wie bei Teile und Herrsche besteht das Ziel darin, ein "großes" Gesamtproblem in kleinere Subprobleme zu zerlegen und deren Lösungen zu speichern. Bei "Teile und Herrsche" geschieht das unter Einsatz von Rekursion und Memoizing und beim "Dynamischen Programmieren" (konzeptionell) in einer Tabelle und iterativ (FOR-Schleife). Teile und Herrsche arbeitet top down. Dynamic Programming bottom up: Es berechnet die Lösungen für alle möglichen Subprobleme, auch wenn sich später herausstellt, dass einige davon zur Lösung des komplexen Ausgangsproblems gar nicht erforderlich sind. Auf jeden Fall kann dadurch sichergestellt werden, dass beim Zusammenbau der Gesamtlösung keine Teillösungen fehlen!
Für Dynamic Programming ist die Gültigkeit der Bellmanschen Optimalitätsbedingung wichtig, d.h. die optimale Lösung des Gesamtproblems muss sich zwangsläufig aus den optimalen Lösungen der Teilprobleme ergeben. Da sich Teilprobleme in mehreren größeren Problemen wiederfinden können, kann durch das Speichern der Lösungen ein Effizienzgewinn erzielt werden. Deshalb wird zusätzlicher Speicherplatz investiert, um den Algorithmus zu beschleunigen (Trade space for time).
Das wichtigste Strukturierungsmittel von Dynamic Programming ist eine Tabelle. Die Felder der Tabelle enthalten Werte, die das jeweilige Optimum darstellen. Für deren Berechnung könnte man die mit Teile und Herrsche entwickelte rekursive Verschrift (zusammen mit Memoizing) einsetzen. Klassisches Dynamisches Programmieren sieht jedoch eine schrittweise Berechnung der Feldelemente vor. Bis auf genau ein Feld der Tabelle sind alle Werte Zwischenwerte, auf die die Folgeberechnungen zurückgreifen, ohne sie erneut zu berechnen. Für diese Berechnungsabläufe ist die Reihenfolge der Bestimmung der Teillösungen wichtig. Bei Teile und Herrsche spielt die Reihenfolge keine Rolle.
Diese Charakteristik hebt die Überlegenheit des rekursiv definierten Top-Down-Verfahrens (Teile und Herrsche) gegenüber dem Dynamic Programming Bottom-up-Verfahren hervor. Um letzteres umsetzen zu können, muss die rekursive Lösungsform in eine Iterationn umformuliert werden. Dies eine Fehlerquelle. Außerdem werden durch die rekursive Berechnung nicht alle Tabellenfeldinhalte ermittelt. Um Mehrfachberechnungen auszuschließen wird Memoizing eingesetzt.
Natürlich erhält man DP-Verfahren nicht nur als Alternative zu Teile-und-herrsche-Algorithmen durch Transformation. Die klassische Grundidee (bottom up und Tabelle) dient in vielen Fällen als tragfähige Lösungsstrategie, so etwa wie beim Bellman-Ford-Algorithmus und beim CYK-Verfahren (Cook, Younger, Kasami; Lösung des Wortproblems für kontextfreie Sprachen). Außerdem können auf Basis der Tabellenvorstellung mitunter bestimmte Effizienzverbesserungen nachträglich eingebracht werden.
Inhaltsverzeichnis |
Fibonacci-Zahlen
Ein Beispiel, für welches Teile und Herrsche benutzt werden kann, sind die Fibonacci-Zahlen. Es ist sehr einfach, die rekursive Bildungsvorschrift anzugeben:
$$ fib(n) = \begin{cases} 0, & \text{wenn $n=0$} \\ 1, & \text{wenn $n=1$} \\ fib(n-1) + fib(n-2), & \text{sonst} \end{cases} $$
Dies lässt sich auch schnell programmieren:
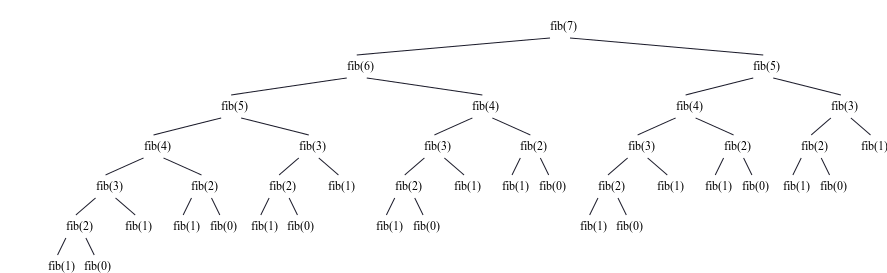
Rekursionsbaum
Rekursive Berechnung mit Memoizing
Analysiert man die Zeitkomplexität des oben beschriebenen Algorithmus, so ergibt sich ein exponentieller Aufwand ($\Theta(\phi^n), \phi>1$), und das für ein Problem, das nicht sehr komplex zu sein scheint. Memoizing kann genutzt werden, um die Fibonacci-Zahlen wesentlich schneller zu berechnen, ohne die rekursive Berechnungsvorschrift transformieren zu müssen. Durch Memoizing fehlen viele Berechnungsäste des Rekursionsbaumes. Er wächst nicht exponentiell, sondern linear.
Die Grundidee besteht darin, jeden Wert nur einmal berechnen zu müssen. Wurde erstmals eine Fibonacci-Zahl ermittelt, so wird sie in einem Zwischenspeicher abgelegt und steht zur Verfügung, sobald sie wieder benötigt wird. Hierfür sollte eine Datenstruktur gewählt werden, mit der man den Wert für einen Key in $\mathcal{O}(1)$ lesen kann. Natürlich bietet sich eine Hashmap (Dictionary für memo) an, die den Parameter $n$ auf $fib(n)$ abbildet, oder ein Array, bei dem die $n$-te Fibonacci-Zahl im Index $n$ steht.
Dynamisches Programmieren (Bottom-up)
Klassisches Dynamic Programming ist ein Bottom-Up Verfahren, also ein Algorithmus, der bei einem Blatt des Rekursionsbaums beginnt und schrittweise die nächstgrößeren Werte berechnet. Bei den Fibonacci-Zahlen ist der Bottom-Up Ansatz relativ intuitiv: Ausgehend von den bereits gegebenen Werten von $fib(0)=0$ und $fib(1)=1$ berechnet man in einer Schleife von 2 bis $n$ schrittweise den jeweils nächstgrößeren Wert. Da zur Berechnung einer Fibonacci-Zahl, die zwei nächstkleineren Fibonacci-Zahlen benötigt werden, ist sichergestellt, dass die jeweils benötigten Werte vorliegen, denn die Schleife arbeitet "von klein zu groß".
In folgendem nichtrekursiven Programm ist deshalb eine Zählschleife zu sehen.
In beiden Fällen müssen $n$ Fibonacci-Zahlen berechnet werden, deren Zeitaufwände lediglich in $\mathcal{O}(1)$ liegen, da die Werte entweder durch die Verwaltung der Rekursion (Aufstieg aus der Tiefe) oder durch die Ausführung der Schleife bereits vorliegen. Somit ergibt sich insgesamt ein Zeitaufwand in $n \cdot \mathcal{O}(1) = \mathcal{O}(n)$.
Das 0/1-Rucksack-Problem
Um das 0/1-Rucksack-Problem zu lösen, kann Dynamic Programming ebenfalls benutzt werden. Für eine Menge von $n$ Gegenständen, deren individuelles Gewicht und zugehöriger Wert vorgegeben sind, ist eine Auswahlentscheidung zu treffen: Mitnahme des betrachteten Gegenstandes im Rucksack mit Kapazität $K$ oder nicht. Das Ziel besteht darin, den Gesamtwert (Summe aller Werte der eingepackten Gegenstände) zu maximieren, ohne mit der Gewichtssumme die Rucksackkapazität $K$ zu überschreiten.
In der folgenden rekursiven Definition des maximalen Gesamtwertes sind $i$ der Index des letzten Gegenstandes in der Gegenstandsliste und $K$ die Kapazität (das maximal zulässige Gewicht, welche der Rucksack tragen kann).
$$value(i,k)=\begin{cases} 0, & \text{wenn $i=0$}\\ value(i-1,k), & \text{wenn $i>0 \text{ und } w[i]>k$}\\ \max(value(i-1,k), value(i-1,k-w[i]) + v[i]), & \text{sonst} \end{cases}$$
$i=0$ bedeutet, dass kein einziger Gegenstand in den Rucksack gepackt wird. Der Gesamtwert ist damit gleich 0. Wenn ein weiterer Gegenstand verfügbar ist, mit dessen Aufnahme jedoch die Rucksack-Restkapazität überschritten werden würde, ist der erreichbare Wert gleich dem Wert der Rucksackbefüllung ohne diesen Gegenstand, d.h. nur bis einschließlich Gegenstand $i-1$. (Dies bedeutet nicht, dass sich Gegenstand $i-1$ zwangsläufig im optimalen Rucksack befinden muss.)
Wir interpretieren nun die obige rekursive Formel. Wenn der Gegenstand prinzipiell in den Rucksack passt, d.h. die Restkapazität nicht überschreitet, fragt man nach dem größeren der beiden erzielbaren Gesamtwerte:
1. Nimmt man den Gegenstand $i$ in den Rucksack auf, ergibt sich der Wert aus der Summe des Wertes dieses Gegenstands und dem erreichbaren Maximalwert des kleineren Rucksacks, der die Gegenstandsliste bis $i-1$ berücksichtigt. Die dafür verbleibende Restkapazität wird dann allerdings um das Gewicht des $i$-ten Gegenstands verringert.
2. Nimmt man den Gegenstand $i$ nicht in den Rucksack auf, bleibt es bei dem über die Gegenstände $0$ bis $i-1$ zu ermittelnden max. Gesamtwert, wofür dann allerdings eine unverminderte Restkapazität zur Verfügung steht.
Gesucht ist der Wert $value(n,K)$. In folgendem Programm findet sich am Ende der Aufruf value(n, K) bzw. value_memo(n, K).
Ohne dynamisches Programmieren handelt es sich um einen Exponentialzeit-Algorithmus. $k$ und $i$ stellen die Problemgröße dar. Um den Wert eines Problems mit der Größe $i$ zu berechnen, muss bis zu zweimal (im sonst-Fall) der Wert eines Problems der Größe $i-1$ berechnet werden. Das heißt die Zeit zur Berechnung der Lösung verdoppelt sich mit jedem Inkrement von $i$, was zu einer exponentiellen Laufzeit führt.
Durch dynamisches Programmieren kann dies verbessert werden. Anstatt das gleiche Teilproblem immer wieder neu zu berechnen, wird die Lösung in einem Dictionary mit dem Parameter-Paar als Schlüssel gespeichert. Memoizing! Nun kann in vielen Fällen, der Wert aus dem Dictionary wiederverwendet, d.h. in $\mathcal{O}(1)$ gelesen, werden. Da jeder Wert nur einmal berechnet werden muss, ist die Zeit, um das Gesamtproblem zu lösen, das Produkt aus der Anzahl der Teilprobleme und der Zeit für deren Lösung.
Die Zahl der Teilprobleme ist durch die Anzahl $nK$ aller möglichen Tupel $\{1,\ldots,n\}\times\{0,\ldots,K\}$ beschränkt, was sich in einer dem entsprechenden Tabelle niederschlägt. Folglich liegt die Laufzeit des Problems in $\mathcal{O}(nK) \cdot \mathcal{O}(1) = \mathcal{O}(nK)$.
Dies lässt zunächst vermuten, dass wir es geschafft haben, einen Polynomialzeit-Algorithmus für das Rucksackproblem zu entwickeln. Das trifft im Allgemeinen jedoch nicht zu, denn der Wert der Zahl $K$ gehört zur Problemgröße. Das ist sinnvoll, da mit steigendem $n$ auch $K$ anwachsen muss, um eine sinnvolle Problemstellung vorzulegen.
Da Zahlen in einem Computer jedoch nicht unär, sondern mit der Basis 2, dargestellt werden, verdoppelt sich die Größe von $K$ mit jedem Hinzufügen einer Ziffer. Auf die Stelligkeit bezogen hat der Algorithmus also eine Komplexität von $\mathcal{O}(n \cdot 2^k)$. Man spricht in diesem Fall von einem Algorithmus mit pseudo-polynomialer Laufzeit, die als exponentiell angesehen werden muss.
Im Gegensatz zur Berechnung der Fibonacci-Zahlen bleibt das 0/1-Rucksackproblem ein solches, für dessen Lösung bisher kein Polynomzeit-Algorithmus bekannt ist. Die Chancen einen solchen zu finden, stehen leider sehr schlecht.
Beispiel: Zum Abschluss der Betrachtung des 0/1-Rucksackproblems wenden wir die obigen Überlegungen auf ein einfaches Beispiel an. Gegeben ist die folgende (unsortierte) Gegenstandsliste mit $n=4$ Elementen. Die Kapazität des Rucksacks beträgt $K=5$.
| i | 1 | 2 | 3 | 4 |
|---|---|---|---|---|
| v | 100 | 20 | 60 | 40 |
| w | 3 | 2 | 4 | 1 |
Die im Folgenden aufgestellte Tabelle verwendet die folgenden Ausfüllregeln.
- $value[0,k]=0$
- Tabelle zeilenweise ausfüllen, beginnend mit $i=0$.
Wenn $w[i]>k$,
dann $value[i,k]=value[i-1,k]$,
sonst $value[i,k]=max(value[i-1,k], v[i]+value[i-1,k-w[i]])$
Die Formeln geben an, dass man die erforderlichen Zwischenwerte in der vorhergehenden Zeile ($i-1$) in der angegebenen Spalte findet.
| i\k | 0 | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 0 | 100 | 100 | 100 |
| 2 | 0 | 0 | 20 | 100 | 100 | 120 |
| 3 | 0 | 0 | 20 | 100 | 100 | 120 |
| 4 | 0 | 40 | 40 | 100 | 140 | 140 |
Der Eintrag im untersten rechten Tabellenfeld repräsentiert das Ergebnis: $value[n,K]=value[4,5]=140$.
Interessiert man sich für genau die in den Rucksack eingepackten Gegenstände, so ist eine Rückrechnung erforderlich.
i = n;
k = K;
while i, k > 0 do
if value[i, k] != value[i - 1, k] then
markiere das i-te Element;
k = k - w[i];
endif;
i = i - 1;
Ergebnis: Genau die Gegenstände 1 und 4 werden in den Rucksack gepackt. Deren Gewichtssumme beträgt $4$ ($4<5$) und deren Gesamtwert ist $140$.
Fazit: Wie dieses Beispiel illustriert, ist die top-down-Verarbeitung, d.h. Verwendung von Rekursion in Verbindung mit Memoizing, schon deshalb eine ernst zu nehmende Alternative zur klassischen bottom-up-Strategie (mit Schleifen), da man den rekursiven Lösungsansatz schnell findet und dessen fehleranfällige Transformation in ein iteratives Verfahren nicht braucht. Die rekursive Lösung findet sich in den Ausfüllregeln für die Tabelle unmittelbar wieder.
Bellman-Ford(-Moore)-Algorithmus
Dynamic Programming kann auch zur Lösung des Single-Source Shortest Path Problem angewandt werden: Gesucht ist der kürzeste Weg von einer Quelle zu einem beliebigen Knoten in einem gewichteten Graphen. Im Gegensatz zum Dijkstra-Algorithmus kommt er auch mit negativen Kantengewichten zurecht. Zyklen mit negativen Kantensummen müssen jedoch ausgeschlossen werden, da deren mehrfaches Durchlaufen den Gesamtweg systematisch verkürzen würde.
Der Bellman-Ford-Algorithmus wurde in den Jahren 1956-1958 von Richard Bellman, Lester Ford und Edward F. Moore veröffentlicht. Der asymptotische Zeitaufwand beträgt $\mathcal{O}(\lvert V \rvert \cdot \lvert E \rvert)$. Dieser Algorithmus und darauf aufbauende Verfahren sind prinzipiell für das Routing in Netzwerken geeignet, werden aber heute von anderen Verfahren verdrängt.
Knotenorientiertes Vorgehen
Da es sich um Dynamic Programming handelt, stellt sich die Frage, was die Subprobleme sind. Gesucht ist der kürzeste Weg $weg(v,k)=(s, w_1,..., w_{k-1}, v)$, von $s=w_0$ nach $v=w_{k}$.
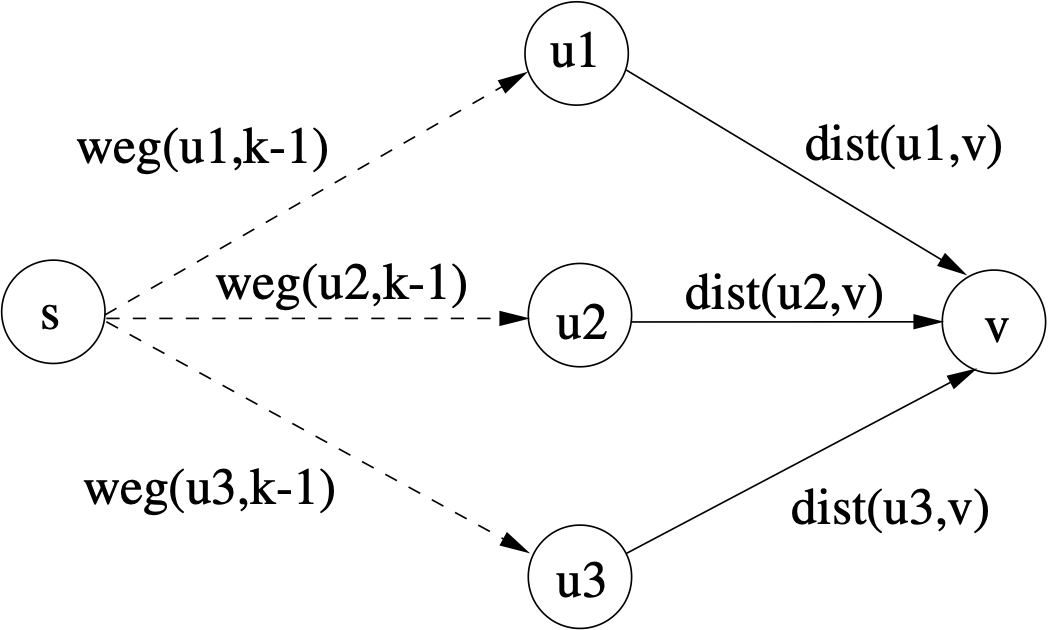
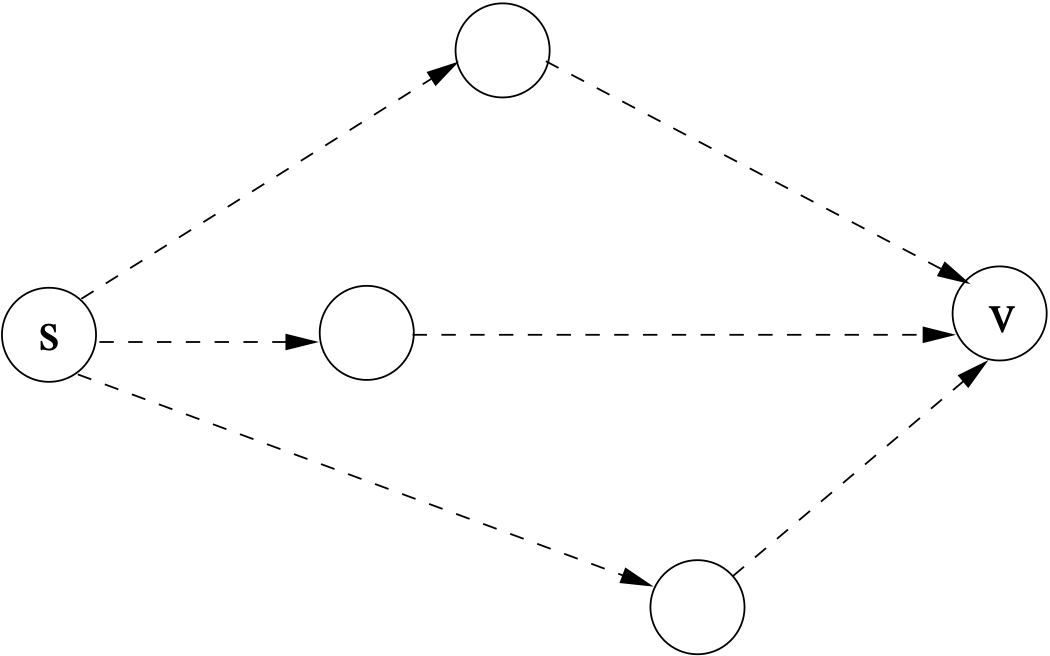
Um diesen zu ermitteln, braucht man den kürzesten Weg $weg(u,k-1)=(s, w_1,..., u)$, von $s=w_0$ nach $u=w_{k-1}$ (in Zeile $k-1$ einer Tabelle). Zur Bestimmung von $weg(v,k)$ (in Zeile $k$ einer Tabelle) ermitteln wir also das Minimum der Summen $weg(u,k-1)+dist(u,v)$ für alle Vorgängerknoten $u$ von $v$:
Die Abb. zeigt beispielhaft drei Vorgängerknoten $u\in v.pre$. Mit dieser Erkenntnis lässt sich die folgende rekursive Gleichung aufstellen. $v$ ist der Knoten, zu dem der kürzeste Weg von $s$ (Startknoten) aus gefunden werden soll. $v.pre$ bezeichnet die Menge der Vorgängerknoten von $v$. (Man könnte auch alle Knoten $u$ herausgreifen, für die $v$ in der Adjazenz-Liste von $u$ enthalten ist.) $k$ ist die Anzahl der maximal zu benutzenden Kanten und $dis(u,v)$ ist das Kantengewicht von $(u,v)$, d.h. die Distanz von $u$ zu $v$. Die obige Abbildung zeigt den beschriebenen Sachverhalt grafisch.
$$bf(v,k)=\begin{cases} 0, & \text{wenn $v=s$}.\\ \infty, & \text{wenn $v \neq s \text{ und } k=0$}.\\ \underset{u\in v.pre}{\text{min}}(bf(u, k-1)+dist(u, v)), & \text{sonst}. \end{cases}$$
Handelt es sich bei $v$ um den Startknoten $s$, so sind die Kosten, um zu $v$ zu gelangen, gleich $0$. Beträgt die Anzahl der maximal zu benutzenden Kanten $0$ und handelt es sich bei $v$ nicht um $s$, so ist $v$ nicht erreichbar und die Funktion gibt $\infty$ zurück. Ansonsten ist die Lösung die kleinste Summe aus dem kürzesten Weg von $s$ zu $u$ unter Verwendung von $k-1$ Kanten, einem Vorgängerknoten von $v$, und dem Gewicht (Distanz) von $u$ zu $v$, also genau einer Kante. Da auf dem kürzesten Weg paarweise verschiedene Knoten liegen, die durch $k-1$ Kanten verbunden sind, gilt $k=|V|$.
Während beim 0/1-Rucksackproblem nicht jeder Gegenstand zwangsläufig in den Rucksack gepackt werden konnte, muss hier in jedem Schritt genau einer der adjazenten Knoten auch wirklich genommen werden.
Beispiel:
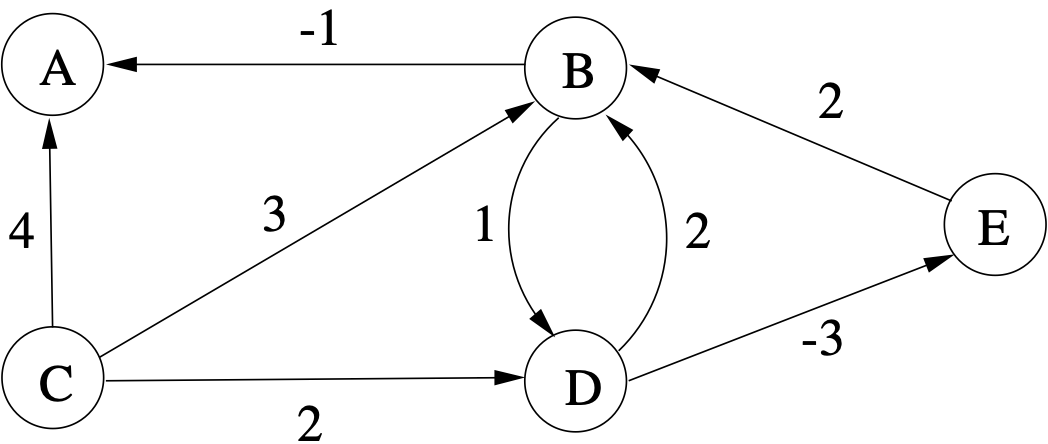
Der kürzeste Weg von $D$ nach $A$ ist $D \stackrel{-3}{\rightarrow} E\stackrel{2}{\rightarrow} B \stackrel{-1}{\rightarrow} A$ und hat eine Länge von $-2$.
| k\V | A | B | C | D | E |
| 0 | $\infty$ | $\infty$ | $\infty$ | 0 | $\infty$ |
| 1 | $\infty$ | 2 | $\infty$ | 0 | -3 |
| 2 | 1 | -1 | $\infty$ | 0 | -3 |
| 3 | -2 | -1 | $\infty$ | 0 | -3 |
| 4 | -2 | -1 | $\infty$ | 0 | -3 |
Diese Tabelle wird zeilenweise ausgefüllt. Dann kann bei der Berechnung eines Feldelements in der $k$-ten Zeile auf die erforderlichen Werte in der $k-1$-Zeile zugriffen werden. (Der Zeilenindex steht hier im zweiten Argument.) Wir zeigen dies am Beispiel von
In folgendem Programm werden diese Beispieldaten verwendet.
Kantenorientiertes Vorgehen
Das Ziel besteht darin, für jede Kante $(u,v)$ des Graphen eine Verringerung der aktuellen Weglänge von $s$ zu $v$ zu erzielen, falls das möglich ist. Für sämtliche mit $\infty$ initialisierten Wege besteht die berechtigte Hoffnung, dass sie sich verkürzen lassen. Eine Idee, wie man diese Weglängenaktualisierung vornehmen kann, entnimmt man der folgenden Abbildung.
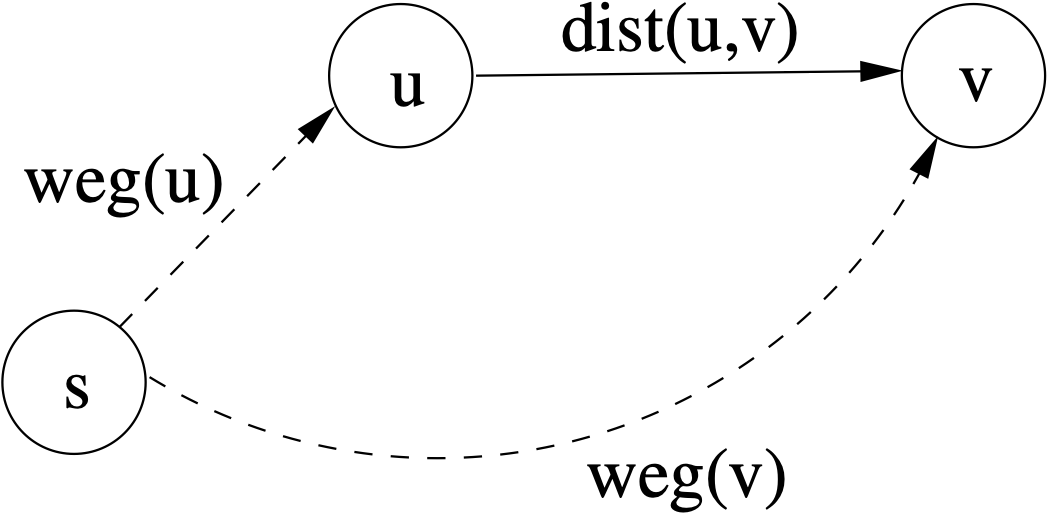
$weg(u)$ bezeichnet den kürzesten Weg vom Startknoten $s$ zum Knoten $u$. $weg(v)$ ist die bisher geringste Weglänge von $s$ zu $v$. Sie wird unterboten, wenn
Wenn diese Ungleichung gilt, aktualisiert man auch den Vorgänger (also $u$) für die spätere Rekonstruktion der Knotenfolge als kürzesten Weges. Anderenfalls belässt man den aktuell vorliegenden Eintrag.
Dieser Vorgang wird $\lvert V \rvert - 1$ mal wiederholt, da der kürzeste Weg zwischen zwei Knoten maximal über $\lvert V \rvert - 1$ Knoten verläuft. (Zyklen sind ausgeschlossen, da sie die Weglänge vergrößern würden.) Sollte sich herausstellen, dass für $\lvert V \rvert$ Iterationen sich kürzere Wege ergeben als nach $\lvert V \rvert - 1$ Iterationen, so muss es einen negativen Kreis (negative weight cycle) innerhalb des Graphen geben. Andernfalls wurden die kürzesten Wege ausgehend vom Startknoten gefunden und es existiert kein negativer Kreis im Graphen.
Der folgende Pseudocode fasst die Überlegungen zusammen:
01 für jedes v aus V 02 weg(v) := unendlich, Vorgänger(v) := keiner 03 weg(s) := 0 04 wiederhole n − 1 mal 05 für jedes (u,v) aus E 06 wenn (weg(u) + dist(u,v)) < weg(v) dann 07 weg(v) := weg(u) + dist(u,v) 08 Vorgänger(v) := u 09 für jedes (u,v) aus E 10 wenn (weg(u) + dist(u,v)) < weg(v) dann 11 STOPP mit Ausgabe „Es gibt einen Zyklus negativen Gewichtes.“ 12 Ausgabe weg, Vorgänger
Wir wenden das Verfahren nun auf das obige Beispiel an, das wir im Folgenden zitieren.
Für die Implementation dieser Variante des Bellman-Ford Algorithmus wird nicht die oben definierte Datenstruktur Node, sondern eine Liste aller Knoten (identifiziert als String) und eine Liste aller Kanten genutzt.
Dieser Ausgabe lässt sich entnehmen, dass der kürzeste Weg von d nach a das Gewicht -2 hat: d (-3) e (2) b (-1) a. -3 + 2 -1 = -2.
Durch die zwei Schleifen ist ersichtlich, dass der Bellman-Ford Algorithmus eine Laufzeit von $\mathcal{O}(\lvert V \rvert \cdot \lvert E \rvert)$ hat. Damit ist er ineffizienter als vergleichbare Algorithmen, wie der Dijkstra Algorithmus, jedoch hat Bellman-Ford den Vorteil, dass er mit negativen Gewichten der Kanten umgehen kann und das korrekte Ergebnis liefert.
Sucht man die kürzesten Wege zwischen allen Knotenpaaren eines Graphen, liegt der Zeitaufwand in $\mathcal{O}(|V|^2\cdot |E|)$. Dann ist ggf. der Floyd-Warshall-Algorithmus vorzuziehen: Er basiert auch auf Dynamischem Programmieren und hat einen Aufwand in $\mathcal{O}(|V|^3)$. Die Idee dieses Verfahrens lässt sich nach dem Vorbild von Bellman-Ford in folgender Abbildung verdeutlichen:
Die Knoten seien mit $k=1,2,3,\ldots,n$ durchnummeriert. Dann kann der kürzeste Weg von $i$ zu $j$ rekursiv definiert werden: $$w[i,j] = \min_k\{w[i,j], w[i,k]+w[k,j]\}.$$ Dies ergibt eine Tabelle mit $k$ Zeilen und $k$ Spalten - typisch für Dynamic Programming.
Rundreiseproblem
Ein ganz ähnliches Problem wie die Kürzeste-Wege-Fragestellung ist die Frage nach der kürzesten Rundreise, die alle vorgegebenen Städte genau einmal besucht. Es ist unter dem Namen Traveling Salesman Problem (TSP) bekannt. Die Planung solcher Touren ist sicher nicht nur für die Auftrittsplanung von Künstlern und für Reiseunternehmen mit logistischem Anspruch von Interesse.
Intuitiv stellt sich die Vermutung ein, dass es sich hierbei um einen Sonderfall des o.g. Problems handelt, für das sich eine Lösung mit den vorgestellten bzw. genannten Algorithmen in $\mathcal{O}(n^3)$ oder sogar $\mathcal{O}(n^2)$ ergibt. $n$ ist die Anzahl der beteiligten Städte. Die Intuition trügt: Bis heute ist kein Verfahren bekannt, dass das Rundreiseproblem mit weniger als exponentiellem Zeitaufwand (exakt) löst. Nur Näherungsverfahren schaffen das.
Leider kann dynamisches Programmieren an dieser Tatsache nichts ändern. Wir prüfen die Anwendbarkeit: In der Tat ist die Optimalitätsbedingung erfüllt. Ein Weg, der o.B.d.A. bei Stadt $i=1$ beginnt (und endet), direkt zu der $e_{i,j}$ entfernten Stadt $j$ führt und danach auf dem Weg zurück zu Stadt $1$ alle Städte aus $\{2,3,4,\ldots,n\}\setminus\{j\}$ genau einmal besucht, ist minimal, wenn eben dieser Weg von $j$ nach $1$ minimal ist.
Auf dieser Basis können wir ein Top-Down-Lösung wie folgt beschreiben. Natürlich gehen wir davon aus, dass eine Adjazenzmatrix mit den entsprechenden Entfernungen $e$ zwischen je zwei Stäten vorliegt. Mit $S=\{2,3,4,\ldots, n\}$ gilt
$$weg(i,S)=\begin{cases} e_{i,1}\ , & \text{wenn $S=\emptyset$}.\\ \min_{j\in S}(e_{i,j} + weg(j, S\setminus\{j\}), & \text{ sonst}.\\ \end{cases}$$
Der Funktionswert $weg(1,S)$ liefert den kürzesten Rundweg.
Für ein iteratives Verfahren einer Bottom-up-Lösung organisiert man eine Tabelle mit $n$ Spalten, nämlich für $2,3,4,\ldots,n,1$, und $2^{n-1}$ Zeilen für alle möglichen Städtemengen, d.h. für die Potenzmenge $\wp(S\setminus\{1\})$. Das ergebnistragende Feld in der Tabelle ist das in Zeile $\{2,3,4,\ldots,n\}$, Spalte $1$. Wenn man zur Berechnung jedes Tabellenfeldes einen linearen Aufwand veranschlagt, ergibt sich insgesamt $\mathcal{O}(n^22^n)$.
Beispiel: Wir betrachten ein asymmetrisches TSP mit folgender Entfernungsmatrix
| e[i,j] | 1 | 2 | 3 | 4 |
|---|---|---|---|---|
| 1 | $\infty$ | 20 | 15 | 10 |
| 2 | 8 | $\infty$ | 9 | 8 |
| 3 | 6 | 12 | $\infty$ | 13 |
| 4 | 5 | 10 | 9 | $\infty$ |
Die Tabelle für Dynamic Programming (Buttom up) hat folgende Struktur. Zu beachten ist, dass sich der erste Parameter von >weg(i,S) aus dem Spaltenindex ergibt.
| $\wp$(S)\i | 2 | 3 | 4 | 1 |
|---|---|---|---|---|
| $\emptyset$ | 8 | 6 | 5 | $\infty$ |
| {2} | $\infty$ | 20 | 18 | 28 |
| {3} | 15 | $\infty$ | 19 | |
| {4} | ||||
| {2,3} | 29 | |||
| {2,4} | ||||
| {3,4} | ||||
| {2,3,4} | 35 |
Die Ausfüllregeln der Tabelle folgen der obigen rekursiven Vorschrift, die für das top-down-Verfahren entwickelt wurde.
Geldwechselproblem
Beim geht es darum, einem Kunden für die Restgeldbetrag-Rückgabe möglichst wenige Münzen heraus zu geben. Es wird also zunächst nach allen möglichen Münzkombinationen, die einen vorgegebenen Betrag ergeben, gefragt. Unter diesen sucht man dann die mit den wenigsten Geldstücken heraus. Dabei ist eine Liste aller verfügbaren (positiven) Münzprägungen (1ct, 2ct, 5ct, 10ct, 50ct, 100ct=1€, 200ct=2€) gegeben. Es wird angenommen, dass alle Münzwerte beliebig oft zur Verfügung stehen.
Für die Lösung des Geldwechselproblems gibt es auch ein Greedy-Verfahren.
Ein entsprechender Dynamic-Programming-Ansatz ergibt sich folgendermaßen: Angenommen, man möchte 54ct wechseln und die verfügbaren Münzprägungen sind: 20ct, 10ct, 5ct und 2ct. Wir betrachten nur die erste dieser vier Münzprägungen, nämlich 20ct. Zunächst könnte man sich entscheiden, kein 20ct-Stück zu benutzen und lediglich die in der sortierten Liste der Münzprägungen nachfolgenden Münzstücke verwenden. Man könnte sich auch entscheiden, genau ein 20ct-Stück zu verwenden. In diesem Fall müssen mit den restlichen Münzen nur noch 34ct gewechselt werden. Genauso könnten genau zwei 20ct-Stücke verwendet werden und entsprechend 14ct mit den restlichen Münzen zusammengelegt werden. Die Möglichkeit, drei 20ct-Stücke zu verwenden, steht nicht zur Verfügung, da dies bereits die 54ct überschreiten würde.
Allgemein gilt: Sei $N$ der zu wechselnde Betrag und $k$ der Wert der zu untersuchenden Münze, so kann die Münze $0$-mal bis $n = \left\lfloor\frac{N}{k}\right\rfloor$-mal verwendet werden.
Hinweis. $f: \mathbb{R} \to \mathbb{Z}$ mit $f(x) = \lfloor x \rfloor$ beschreibt die floor-Funktion, bei der die Zahl auf die nächst kleinere ganze Zahl abgerundet wird.
Jetzt müssen für die rekursive Definition noch die Elementarfälle gebildet werden. Beträgt der zu wechselnde Betrag $N = 0$, so gibt es genau eine Möglichkeit, diesen Betrag zu bilden, nämlich indem man keine Münze verwendet. Ist der zu wechselnde Betrag $N$ negativ, so gibt es keine Möglichkeit diesen Betrag zu bilden, da alle Münzen einen positiven Wert haben.
Weitere Dynamic-Programming-Algorithmen
Es gibt eine Reihe von Verfahren, die nach dem Dynamic-Programming-Prinzip arbeiten. Zwei davon sind:
- CYK-Verfahren zur Feststellung, ob ein Wort der Länge $n$ zur Sprache $L(G)$ gehört oder nicht. $G$ ist eine kontextfreie Grammatik in Chomsky-Normalform. Die Komplexität von CYK beträgt $\mathcal{O}(n^3)$.
- Die Matrix-Kettenmultiplikation gewinnt eine verbesserte Komplexität in Höhe von $\mathcal{O}(n^3)$ durch Veränderung der Auswertungsreihenfolge der Multiplikation der $n$ Matrizen.