Branch and Bound
Aus ProgrammingWiki
Die Idee von Branch and Bound (Verzweige und Begrenze) wurde 1960 von A. H. Land und A. G. Doig formuliert. 1965 gab R. J. Dakin einen einfach zu implementierenden Algorithmus dafür an.
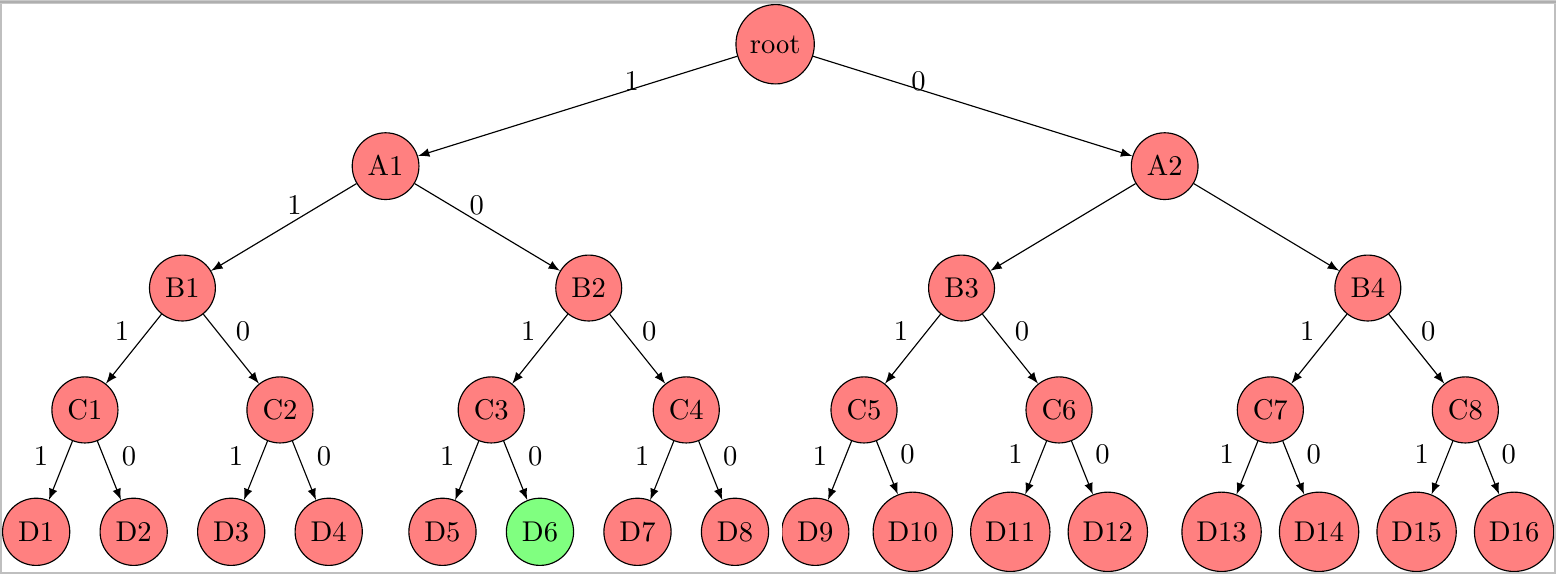
Teile und Herrsche sowie dynamisches Programmieren zerlegen das Gesamtproblem in einfachere Teilprobleme. Im Gegensatz dazu wird bei Branch and Bound die Lösungsmenge geeignet partitioniert. Das bedeutet, dass sich der Lösungsraum baumartig strukturieren lässt. Abb. 1 zeigt das für einen Entscheidungsbaum (gewurzelter, markierter Binärbaum).
Für die kompletten Bäume gilt jedoch, dass sie nur in Exponentialzeit erzeugt und nicht vollständig gespeichert werden können. Man stelle sich z.B. ein 0/1-Rucksackproblem mit nur 50 Gegenständen vor. Bei diesem gibt es über eine Billiarde potentielle Rucksackbelegungen, die nicht alle geprüft werden können. Für ein 0/1-Rucksackproblem mit $4$ Gegenständen könnte Abb. 1 die vollständige Enumeration als kompletten Binärbaum mit Lösung bei (z.B.) $D6$ darstellen.
Das Ziel von Branch and bound ist es, eine vollständige Enumeration bzw. einen vollständigen Durchlauf (Traversierung) des Lösungsraumbaumes zu vermeiden, schon wenn man einigermaßen praktikable Problemgrößen im Auge hat. Dies erreicht man, wenn der Baum nur teilweise, nämlich nur für "aussichtsreiche" Knoten aufgebaut wird.
Durch Verzweigen (Branch-Schritt) entstehen Teilmengen, die jeweils unterschiedliche spezielle Eigenschaften besitzen: Die Gegenstandsmenge beim 0/1-Rucksackproblem kann z.B. in die Teilmenge $A$ alle Rucksackbelegungen, bei denen Gegenstand 1 enthalten ist, und die Teilmenge $B$ alle Rucksackbelegungen, bei denen Gegenstand 1 nicht enthalten ist, zerlegt werden. Diese Mengen können nun wieder "verzweigt" bzw. bezüglich des Enthaltens der anderen Gegenstände in noch speziellere Teilmengen gegliedert werden. So entsteht ein Entscheidungsbaum, wie in Abb. 1. Die jeweils linke und mit $1$ markierte Kante bedeutet "Mitnahme" und die rechte, jeweils mit $0$ markierte Kante verlangt den betrachteten Gegenstand nicht einzupacken. Alternativ zu Entscheidungsverfahren können Tiefensuche oder Breitensuche als Enumerationsverfahren eingesetzt werden, um den gewünschten Baum zu erhalten.
Für die Identifikation "hoffnungsloser Fälle", also Knoten, die (zunächst) nicht weiter expandiert werden, ist eine separate Knotenbewertung (untere und obere Schranke) notwendig (Bound-Schritt). Eine (geeignete) obere Schranke bei einem Maximierungsproblem beziffert den für den betrachteten Knoten größtmöglichen erzielbaren Maximalwert. Der durch einen Knoten repräsentierte, bereits erzielte Maximalwert dient als (globale) untere Schranke für das globale Maximum. Diese Schranke wird im Prozess schrittweise nach oben verschoben wird. Ist die obere Schranke eines Knotens kleiner als dessen untere, wäre die Expansion des betreffenden Knotens sinnlos. (Für Minimierungsprobleme gilt das Ganze analog.)
An die Stelle einer vollständigen Enumeration tritt eine erfolgsorientierte Expansion des Lösungsraumbaumes in jeweils drei Schritten:
- Branch: Partitionierung der Lösungsmenge
- Search: Auswahl des nächsten zu expandierenden Knotens
- Bound: Berechnung der unteren und oberen Schranke für den ausgewählten Knoten und Prüfung, ob dieser weiter betrachtet werden muss
Inhaltsverzeichnis |
0/1-Rucksackproblem
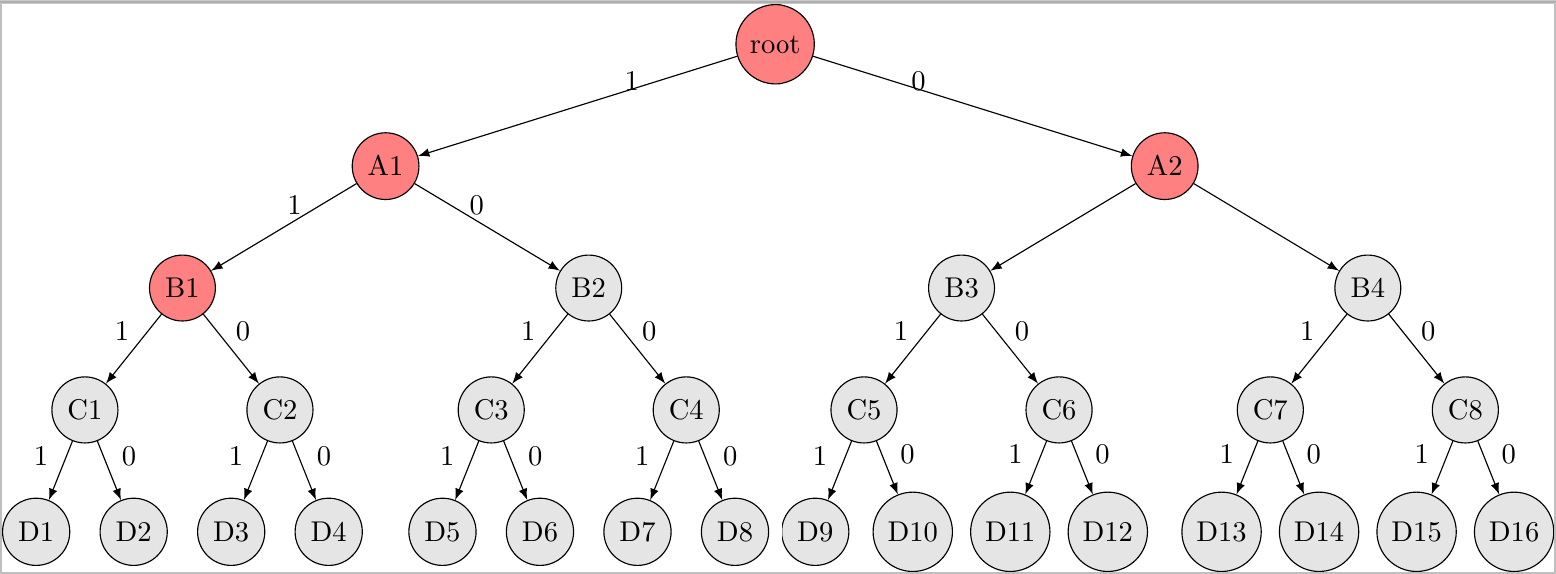
Für ein 0/1-Rucksackproblem mit 4 Gegenständen könnte genau der in Abb. 1 dargestellte vollständige Baum entstehen. Der Baum hat $2^5-1=31$ Knoten. Wie wir weiter unten sehen werden, besitzt der mittels Branch-and-Bound reduzierte Baum nur $4$ Knoten. Die nicht verwendeten Knoten wurden in Abb. 2 grau markiert.
Im Unterschied zu dem weiter unten bearbeiteten Rundreiseproblem wird beim 0/1-Rucksackproblem eine Auswahl von (einzupackenden) Gegenständen vorgenommen, während beim Rundreiseproblem alle Städte in der Lösung vorkommen müssen.
Da die Kapazitätsbeschränkung $K$ des Rucksacks Teil der Aufgabenstellung ist, werden die Knoten, durch die das Gesamtgewicht des Rucksacks über $K$ liegen würde, nicht expandiert.
Die ja/nein- bzw. $1$/$0$-Angaben an den Kanten/Pfeilen beziehen sich auf die Knoten, von denen sie ausgehen. Für den Knoten, der den Gegenstand mit dem Gewicht $5$ in der Wurzel repräsentiert, bedeutet das: $1$/ja/links/einpacken bzw. $0$/nein/rechts/nicht einpacken.
Die Kapazitätsgrenze des Rucksacks ist eine statische Schranke, denn sie ändert sich während der Suche nicht. Sie gehört hier zur Aufgabenstellung. Für das Branch and Bound Verfahren sind dynamische Schranken, die im Verlauf der Suche immer strenger werden, von Interesse. Wurde z.B. bereits irgendeine gültige Rucksackbelegung gefunden, können Knoten unter denen nur schlechtere Belegungen zu finden sind, ignoriert werden. Je besser der aktuell beste Rucksack im Verlauf der Suche wird, umso strenger wird die Schranke und umso stärker fällt die Begrenzung aus. Das Ziel ist also möglichst schnell zu einer guten (noch nicht optimalen) Lösung zu gelangen, um von einer möglichst starken Begrenzung zu profitieren.
Beispiel: Gegeben sind 4 Gegenstände mit den Gewichten $g=(5,3,4,2)$ und den Werten $w=(9,5,6,3)$. $K=8$. Unter den gültigen Bepackungen des Rucksacks soll die mit dem größten Gesamtwert ermittelt werden.
| Gegenstand $i$ | Gewicht $g$ | Wert $w$ | spezifischer Wert $w/g$ |
|---|---|---|---|
| 1 | 5 | 9 | 1,8 |
| 2 | 3 | 5 | 1,7 |
| 3 | 4 | 6 | 1,5 |
| 4 | 2 | 3 | 1,5 |
Gibt es z.B. bereits einen gültigen Rucksack mit einem gewissen Wert, so müsste für einen Knoten (quasi einen noch nicht fertig gefüllten Rucksack) bestimmt werden, ob überhaupt noch ein gültiger Rucksack zusammengestellt werden kann, der wertvoller ist. An jedem Knoten hat der untersuchte Teil-Rucksack einen momentanen Gesamtwert und eine Restkapazität. Um zu bestimmen, welcher zusätzliche Gegenstandswert unter Verbrauch der Restkapazität noch hinzugefügt werden kann, müsste allerdings ein weiteres (kleineres) Rucksackproblem gelöst werden. Das wäre sehr aufwendig. Wir brauchen eine effiziente Bewertungsfunktion. Diese Effizienz kann dadurch verbessert werden, dass eine Schranke geringerer Güte ermittelt wird (Relaxation). Dies kommt dann auch bei der näherungsweisen Lösung von Optimierungsproblemen zum Tragen. Für das 0/1 Rucksackproblem bietet sich z.B. folgende Möglichkeit:
Die $n$ Gegenstände mit den Werten $w_i$ und den Gewichten $g_i$ für $1 \leq i \leq n$ können nach ihrem spezifischen Wert $\frac{w_i}{g_i}$ sortiert entschieden werden. Dieser Quotient sagt aus, welcher Wert pro Gewichtseinheit beim Hinzufügen dieses Gegenstands hinzugewonnen wird. Entscheidungen für Gegenstände mit hohem Wert und geringem Gewicht werden so zuerst getroffen. Es ist sichergestellt, dass $\frac{w_i}{g_i} \geq \frac{w_{i+1}}{g_{i+1}}$. Für einen Knoten (einen Teil-Rucksack) bei dem bereits $k$ Gegenstände entschieden wurden, kann bei gegebener Maximalkapazität $K$ die Restkapazität $r$ und der damit einhergehende maximal erreichbare Rucksackwert $m$ bestimmt werden. Ein (Teil-)Rucksack ist definiert durch den Vektor $\overrightarrow{x}=(x_1, x_2, \dots, x_k) \text{ für } 1 \leq k \leq n \text{ und } x_k \in \{0,1\}$. Der Rucksack $(1,0,1)$ enthält demnach Gegenstand 1 und 3 und nicht Gegenstand 2. $$r = K - \sum_{i=1}^k x_i g_i$$ $$m = r \frac{w_{k+1}}{g_{k+1}} + \sum_{i=1}^k x_i w_i$$ Die Restkapazität $r$ eines Rucksacks ist die Differenz zwischen Maximalkapazität $K$ und aktuellem Rucksackgewicht. Der maximal erreichbare Rucksackwert $m$ (obere Schranke für das tatsächliche Maximum) ist die Summe aus dem aktuellen Rucksackwert und der Restkapazität multipliziert mit dem spezifischen Wert des nächsten noch nicht entschiedenen Gegenstands ($k+1$). Da die spezifischen Werte aller weiteren Gegenstände maximal genauso groß sind, bildet $m$ eine obere Schranke.
Liegen für alle aktuellen Blätter die Wert des jeweils besten Rucksacks (untere Schranke) nicht mehr unter dem höchstens erzielbaren Gesamtwert (oberen Schranke), so ist das globale Maximum gefunden. Weitere Knotenexpansionen wären Zeitverschwendung.
Ablauf
Berechne eine globale untere Schranke (= Gesamtwert des aktuell gepackten Rucksacks), falls sie existiert.
Solange das globale Maximum nicht gefunden wurde:
Falls die obere Schranke in jedem expandierbaren Knoten $\leq$ der unteren Schranke ist,
dann wurde das globale Maximum gefunden und STOPP.
Wähle unter den expandierbaren den Knoten $v$ mit größter oberer Schranke.
Berechne einen Nachfolgerknoten durch Expansion des Knotens $v$.
Aktualisiere die untere Schranke, falls erforderlich.
Wir beginnen mit dem Knoten $A$. Die untere Schranke ist $0$. Dessen obere Schranke ergibt sich aus der kleinen Rechnung in der links angegebenen Abbildung aus $14.4$. Damit hat Knoten $A$ aktuell die größte obere Schranke und wird zu $B$ expandiert, indem Gegenstand $1$ eingepackt wird. Der Gesamtwert ergibt sich aus dem Wert von Gegenstand $1$. Also ist $9$ die neue untere Schranke. Die obere Schranke von $B$ ist $14$. Also wird $A$ mit $14.4$ als nächstes expandiert, diesmal zu $C$. Dieser Knoten repräseniert den leeren Rucksack: Gegenstand $1$ wurde nicht eingepackt. $C$ kann mit $13.333...$ nicht mithalten, sodass im nächsten Schritt $B$ zu $D$ expandiert wird. $D$ repräsentiert den mit genau den Gegenständen $1$ und $2$ gefüllten Rucksack. Dieser beachtet die Gewichtsbeschränkung $8$ und hat einen Wert von $14$. Damit wird die untere Schranke global auf $14$ angehoben. Die links angegebene kleine Berechnung ergibt eine obere Schranke für $D$ i.H.v. $14$. Damit gilt nun, dass die untere und obere Schranke gleich sind. Nachtäglich gilt das auch für $B$ und für $C$ ist die obere sogar etwas kleiner als die untere. Damit ist diese Abbruchbedingung für alle aktuell expandierbaren Knoten erfüllt und das Verfahren stoppt. Exemplarisch wollen wir nun doch noch $B$ zu $E$ expandieren. Dieses Experiment endet mit $13.5$ als obere Schranke ohne Chance auf eine bessere Rucksackbefüllung von $E$ aus. Das Ergebnis lautet $(1,1,0,0)$, d.h. die Gegenstände $1$ und $2$ werden in den Rucksack gepackt, die Gegenstände $3$ und $4$ jedoch nicht. Dies ergibt einen Rücksack mit maximalem Gesamtwert i.H.v. $14$. |
Implementation
Nur selten werden Branch and Bound Algorithmen rekursiv implementiert. Eine sortierte Queue (priority queue) ist zumeist die beste Option, um eine Menge abzuarbeitender Elemente zu verwalten, so wie es hier für die Knoten erforderlich ist. Die meisten höheren Programmiersprachen bieten hierzu entsprechende Datenstrukturen an. Hier wird heapq verwendet, um die zur Expandierung zur Verfügung stehenden Knoten nach ihrem maximal erreichbaren Rucksackwert sortiert bereitzustellen. Die Auswahl des als nächstes zu expandierenden Knotens kann so durch ein einfaches heappop realisiert werden.
Die Expandierung, also das Erzeugen neuer Knoten mit und ohne dem nächsten Gegenstand, erfolgt schlicht durch Anhängen von 1 oder 0 an die Liste welche einen Rucksack repräsentiert. Die expandierten Knoten werden nur dann der Queue hinzugefügt, wenn die Kapazitätsgrenze nicht überschritten wird und der maximal erreichbare Wert den momentan besten Rucksackwert überschreitet.
Gibt es keine zu prüfenden Knoten mehr, also wurden alle Knoten entweder bereits verarbeitet oder ausgeschlossen, steht das Endergebnis fest.
Traveling Salesman Problem (TSP)
Das oft zitierte Problem des Handlungsreisenden oder Rundreiseproblem besteht darin, eine vorgegebene Anzahl von Städten genau einmal zu besuchen und zum Ausgangspunkt zurückzukehren, wobei der zurückgelegte Gesamtweg minimal ist. Die Längen der Wegstrecken zwischen den Städten sind bekannt.
Dieses Problem haben aber nicht nur Handlungsreisende, sondern auch Logistikunternehmen (wie muss das Postauto fahren, sodass die Tour möglichst schnell geht), Platinen-Designer (wie müssen Kontakte verbunden werden, sodass möglichst wenig Edelmetall verbraucht wird) und viele mehr. In jedem Fall geht es darum, irgendwelche "Kosten" zu minimieren. Es handelt sich also um ein Optimierungsproblem.
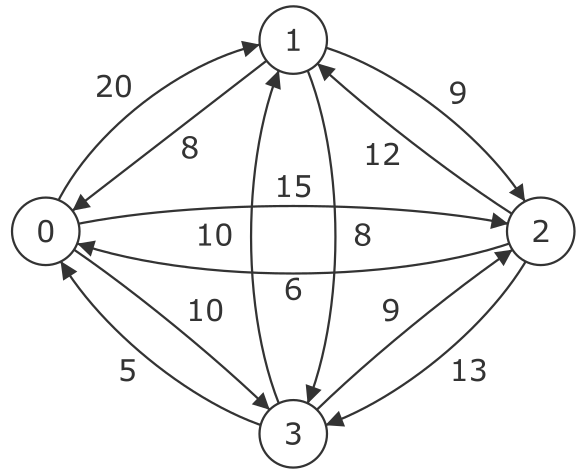
Ein TSP lässt sich sehr einfach in Form von gewichteten Graphen darstellen, s. Abb. 2. Die die Städte repräsentierenden Knoten sind einfach durchnummeriert worden: $0,1,2,3$, $n=4$. Die Gewichte der Kanten entsprechen hier den Kosten für den Übergang von einem Knoten zum anderen (z.B. dem Preis für eine Flugreise von Ort A nach Ort B). Die Kosten zwischen zwei Knoten können dabei auch von der Richtung abhängig sein.
Eine Entfernungsmatrix $E$, wie in Abb. 3, liefert auch eine adäquate Modellierung des gegebenen Sachverhalts. Die $\infty$-Einträge kennzeichnen unmögliche oder verbotene Übergänge.
| $E$ | 0 | 1 | 2 | 3 |
|---|---|---|---|---|
| 0 | $\infty$ | $20$ | $15$ | $10$ |
| 1 | $8$ | $\infty$ | $9$ | $8$ |
| 2 | $6$ | $12$ | $\infty$ | $13$ |
| 3 | $5$ | $10$ | $9$ | $\infty$ |
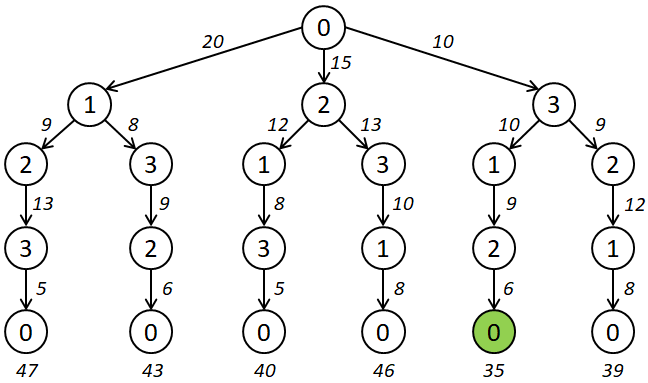
Die Suche nach einem Weg mit minimalen Kosten kann auch hier mittels Entscheidungsbaum visualisiert werden: Die im Baumdiagramm (Abb. 4) jeweils eingetragenen Pfeile geben an, welche Stadt als nächste besucht wird. Da es sich um eine Rundreise handelt, spielt es keine Rolle, welcher Knoten die Wurzel des Baumes (Start und Ende der Rundreise) bildet.
Gibt es $n$ Knoten, so gibt es im ersten Schritt $n-1$ Möglichkeiten die Reise fortzusetzen, im nächsten Schritt nur noch $n-2$ usw. bis nach $n-2$ Schritten nur ein Knoten als mögliches Ziel verbleibt. Mit der Rückkehr zum Ausgangspunkt schließt sich der Kreis und die Länge des Weges steht fest.
Der in Abb. 4 angegebene Baum protokolliert alle möglichen Städtebesuchsfolgen. Für die Suche der kürzesten Rundreise spielt es im Allgmeinen durchaus eine Rolle, auf welchem Weg die betrachtete Stadt erreicht wurde. Von daher brauchen wir für jeden Stadtbesuch im Protokoll (Abb. 4) eine aktualisierte Gesamtschau auf die noch möglichen Fortsetzungen des Weges.
Dies erreichen wir durch Modifikation der jeweils aktuellen Entfernungsmatrix und führen das am Beispiel $0\rightarrow 3$ vor:
- $E[0,j]=\infty$ für $j\neq 3$: Besuche $3$ von $0$ aus, nicht von einer anderen Stadt her.
- $E[3,0]=\infty$: Der Rückweg von $3$ zu $0$ ist verboten, da $0$ bereits besucht wurde.
- $E[i,3]=\infty$ für $i\neq 0$: Nur von $0$ besucht man $3$, von keiner anderen Stadt aus.
Nach dem Übergang von $0$ (Start/Ziel) zu $3$ ergibt sich die in Abb. 5 angegebene modifizierte Entfernungsmatrix.
| $E$ | 0 | 1 | 2 | 3 |
|---|---|---|---|---|
| 0 | $\infty$ | $\infty$ | $\infty$ | $10$ |
| 1 | $8$ | $\infty$ | $9$ | $\infty$ |
| 2 | $6$ | $12$ | $\infty$ | $\infty$ |
| 3 | $\infty$ | $10$ | $9$ | $\infty$ |
Das Verfahren zur Herstellung der (übergangsabhängigen) modifizierten Entfernungsmatrix lässt sich aus obigem Beispiel für $a\rightarrow b$ verallgemeinern, indem wir $0$ durch $a$ und $3$ durch $b$ ersetzen.
- $E[a,j]=\infty$ für $j\neq b$: Besuche $b$ von $a$ aus, nicht von einer anderen Stadt her.
- $E[b,a]=\infty$: Der Rückweg von $b$ zu $a$ ist verboten, da $a$ bereits besucht wurde.
- $E[i,b]=\infty$ für $i\neq a$: Nur von $a$ besucht man $b$, von keiner anderen Stadt aus.
Begrenzung und Ablauf
Um nun dafür zu sorgen, dass der jeweils vielversprechendste Knoten expandiert wird, benötigen wir eine Bewertungsfunktion. Diese soll für die (modifizierte) Entfernungsmatrix eines aktuellen Blattes des sich entwickelnden Baumes eine Schranke bestimmen. Im Falle des TSP muss dies eine untere Schranke für die Länge der kürzesten Rundreise, die auf diesem Weg erzielbar ist, sein. Für die Bewertungen zweier expandierbarer Knoten entscheidet man sich für den mit der besseren Bewertung, um die Expansion mit diesem fortzusetzen. Für diese Entscheidung werden alle aktuell expandierbaren Knoten herangezogen.
Bei der Suche einer geeigneten Bewertungsfunktion machen wir uns folgende Überlegung zunutze: Wenn man die gegebene Entfernungsmatrix $E$ normiert, d.h. alle Zeileneinträge um das jeweilige Zeilenminimum verringert und anschließend alle Spalteneinträge um das jeweilige Spaltenminimum reduziert, ergibt sich eine Matrix $\hat{E}$. Dies entspricht der Idee, eine Stadt auf dem kürzesten Weg zu betreten und auf dem kürzesten Weg zu verlassen. Die kürzeste Rundreise für eine Städteanordnung mit $\hat{E}$ hat mindestens die Länge $0$. Diese Lösung (Städtefolge) stimmt mit der für $E$ überein, nur dass die Rundreiselänge größer ist. Hieraus ergibt sich eine untere Schranke für die kürzeste Rundreise für $E$ aus der Summe aller wie oben gebildeten Zeilen- und Spaltenminima. Abb. w illustriert das beschriebene Vorgehen der Matrixbewertung für den zunächst nur aus der Wurzel $0$ bestehenden Baum in unserem Beispiel. Die kleinen Zahlen ergeben sich aus der Subtraktion des jeweiligen Zeilenminimums vom ursprünglichen Wert in dem betrachteten Feld von $E$. Die kleinen Zahlen verwendet man anschließend zur Bestimmung der Spaltenminima. Im Beispiel beträgt die untere Schranke $35$.
| 0 | 1 | 2 | 3 | Min | |
|---|---|---|---|---|---|
| 0 | $\infty$ | $20_{10}$ | $15_5$ | $10_0$ | $10$ |
| 1 | $8_0$ | $\infty$ | $9_1$ | $8_0$ | $8$ |
| 2 | $6_0$ | $12_6$ | $\infty$ | $13_7$ | $6$ |
| 3 | $5_0$ | $10_5$ | $9_4$ | $\infty$ | $5$ |
| Min | $0$ | $5$ | $1$ | $0$ | $\mathbf{35}$ |
 | Wagenkn_TSP-Schrankenbestimmung.xlsx.zip (0.1 MB) |
Da es nur diesen Wurzelknoten gibt, kann nur dieser im nächsten Schritt expandiert werden. Entscheidet man sich für den Übergang zu Knoten $3$, erhält man die in Abb. 5 angegebene Entfernungsmatrix, die man dem nun aktuellen Blatt zuordnet. Das zugehörige Bound beträgt wiederum $34$, s. Abb. 7.
| 0>>3 | 0 | 1 | 2 | 3 | Min |
|---|---|---|---|---|---|
| 0 | $\infty$ | $\color{red}\infty$ | $\color{red}\infty$ | $10_0$ | $10$ |
| 1 | $8_0$ | $\infty$ | $9_1$ | $\color{red}\infty$ | $8$ |
| 2 | $6_0$ | $12_6$ | $\infty$ | $\color{red}\infty$ | $6$ |
| 3 | $\color{red}\infty$ | $10_{\color{red}1}$ | $9_{\color{red}0}$ | $\infty$ | $\color{red}9$ |
| Min | $0$ | ${\color{red}1}$ | ${\color{red}0}$ | $0$ | $\mathbf{{\color{red}{34}}}$ |
Die $34$ bedeutet, dass es nicht möglich ist, auf diesem Weg eine kürzere Rundreise zu erzielen, als die der Länge $34$. Die tatsächliche minimale Rundreise könnte also durchaus die Länge $40$, jedoch nicht $30$, haben.
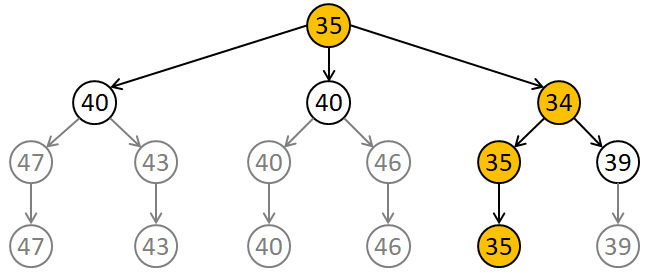
Da der Knoten $0$ durch mögliche Übergänge zu $1$ und $2$ und der Knoten $3$ nach $0\rightarrow 3$ weiterhin expansionsfähig sind, ist ein Bound-Vergleich erforderlich: Wegen $34<35$ wird der Knoten $3$ als nächster expandiert. Geschieht dies mit $3\rightarrow 1$, ergibt sich ein Bound von $35$. Wegen $34<35$ wird wiederum Knoten $3$ expandiert. Hierfür bleibt noch der Übergang $3\rightarrow 2$, was allerdings zu einem Bound von $39$ führt. Da es danach zwei Knoten, nämlich $0$ und $0\rightarrow 3\rightarrow 1$, mit einem Bound von $35$ gibt, ist es gleichgültig, welchen Knoten man als nächstes expandiert. Entscheidet man sich für $0\rightarrow 3\rightarrow 1\rightarrow 2$, ergibt sich wieder ein Bound von $35$. Folglich ist es notwendig, die Wurzel des Baumes, also Knoten $0$ zu expandieren. Sowohl für $0\rightarrow 1$ als auch $0\rightarrow 2$ erhalten wir $40$, sodass wir keine Chance haben, einen kürzeren als den gefundenen Rundweg $0\rightarrow 3\rightarrow 1\rightarrow 2\rightarrow 0$ mit einer Länge von $10+10+9+6=35$ zu finden.
Es ist sehr wichtig, abschließend den Expansionsbaum zur Protokollierung des Ablaufs zu notieren, s. Abb. 8. Die jeweils expansionsfähigen Knoten dieses Baumes sind Wege, die von der Wurzel zu einem der betrachteten Knoten führen, nicht etwa die Knoten selbst. Als Repräsentation der Knoten des Baumes eignen sich die modifizierten Entfernungsmatrizen mit den zugehörigen Bounds.
Der in Abb. 8 dargestellte Baum wird durch Branch and Bound nicht vollständig aufgebaut. Die grau dargestellten Teile entfallen, da die Expansionen chancenlos wären. Durch diese Einsparung kann eine Effizienzverbesserung erzielt werden. Eine Verbesserung der Komplexitätsordnung ist nicht zu erwarten.
Alternative Lösungsraumstruktur: Der Entscheidungsbaum kann auch binär strukturiert werden, sodass man für jeden Knoten entscheidet, ob eine mögliche Kante dem Weg hinzugefügt (linker Ast) oder nicht aufgenommen (rechter Ast) wird. Es lohnt sich, auch diese Form zu bearbeiten.
Implementation
Die Entfernungsmatrix kann sehr einfach als zweidimensionales Array erstellt werden. Zur Repräsentation von Unendlich bieten die meisten höheren Programmiersprachen eine entsprechende Möglichkeit. Mit den Hilfsfunktionen >delta und >modify erfolgt die Berechnung der Schranke und die Anpassung der Entfernungsmatrix bei Festlegung eines Übergangs. Der eigentliche Algorithmus basiert auf einer Priority Queue die stets den erfolgversprechendsten Knoten zur Expandierung bereitstellt (mit unterer Schranke). Sobald ein Endpunkt erreicht ist (alle Knoten sind im Weg enthalten) ist die kürzeste Rundreise gefunden. Anderenfalls erfolgt die Expansion durch Modifizierung der Matrix und Berechnung der zugehörigen Schranke. Die Begrenzung erfolgt in diesem Fall indirekt durch Zurückstellung (nicht Löschung) der Expansion von Knoten mit einer hohen Schranke.