Amortisierte Analyse
Aus ProgrammingWiki
Inhaltsverzeichnis |
Schwächen der Analyse mit dem $\mathcal{O}$-Kalkül
Die asymptotische Aufwandsordnung hat sich als ein sehr gutes objektives Maß für die Leistungsgarantie eines Programms erwiesen. Dies gilt vor allem für worst-case-Aussagen, die sicherstellen, dass der tatsächliche Aufwand die angegebene Schranke für große $n$ keinesfalls übersteigt.
Aus praktischer Sicht kann diese Schranke jedoch zu grob ausfallen. Dies betrifft nicht nur konstante Summanden oder Faktoren in der Funktion für die Aufwandsordnung, sondern diese asymptotische Ordnung selbst. Geht man von einer solchen Analyse aus, sind Fehleinschätzungen für den Einsatz des betrachteten Programms naheliegend.
Für derart pessimistische bzw. unpraktikable Analyseresultate gibt es im Wesentlichen zwei Gründe: 1. Das der Analyse zugrunde liegende Maschinenmodell (Turingmaschine) kann die aktuelle Hardware nicht adäquat widerspiegeln.
- Reale Hardware entfernt sich (durch Pipelining, Parallelismus, Speicherhierarchien usw.) immer mehr von einfachen Maschinenmodellen. Der Einfluss diese Technologien auf den Aufwand der darauf aufsetzenden Berechnungen wird nicht oder nur rudimentär erfasst.
- Andererseits sind ausgeklügelte Algorithmen mitunter nicht implementierbar, obwohl eine theoretische Effizienzaussage vorliegt.
- Umgekehrt werden manchmal innovative Ideen nicht weiterverfolgt, weil sie sich einer vollständigen mathematischen Analyse entziehen.
- Ein weiterer Punkt besteht darin, dass reale Eingaben oft andere als die worst-case-Eingaben der theoretischen Analysen sind.
- Inzwischen hat sich ein noch recht junges Wissenschaftsgebiet etabliert, das sich mit diesen und weiteren Fragen beschäftigt: Algorithm engineering. Die Suche nach neuartigen Analyseverfahren vereint theoretische und experimentelle Ansätze. Damit befassen wir uns hier jedoch nicht.
2. Die Analyse berücksichtigt nicht, wie oft diese aufwandsbewerteten Programmteile im Gesamtprozess zum Einsatz kommen.
- Die klassische $\mathcal{O}$-Kalkül-Analyse ist manchmal viel zu schlecht, nämlich dann, wenn der worst case nur sehr selten eintritt, aber in den meisten Fällen eine wesentlich bessere Laufzeit erzielt wird.
- Die amortisierte Analyse (amortized analysis) betrachtet eine Folge von Operationen, sodass die Aufwände selten/häufig verwendeter Operationen dem entsprechend eingehen. Dadurch erhalten wir eine realistischere Angabe zur Effizienz eines Programms im worst case. Dies gilt besonders dann, wenn die Aufwände der verwendeten Operationen sehr unterschiedlich sind bzw. von vorausgehenden Operationen oder dem Zustand der Datenstruktur abhängen.
Beispiel 1: Binärsuche
Zur Suche eines Elements, das (vermutlich) in einer gegebenen Liste mit $n$ Elementen vorkommt, stehen zahlreiche Verfahren zur Verfügung. Die einfachste Variante besteht wohl darin, jedes Listenelement mit dem gesuchten zu vergleichen. Die Liste wird im worst case solange durchgegangen bis das Element entweder an letzter Position oder überhaupt nicht gefunden wird. Der dafür zu veranschlagende Aufwand beträgt $\mathcal{O}(n)$.
Alternativ kann man die Binärsuche anwenden. Wir haben sie bereits kurz beschrieben.
Statt einen gegebenen Wert in einer unsortierten Liste zu suchen, wird diese zuerst sortiert und anschließend mit dem Binärsuchverfahren ein sehr effizienter Algorithmus angewandt. Als Gesamtaufwand ergibt sich
$$T_{sort}+T_{Binärsuche} = \mathcal{O}(n\log_2n) + \mathcal{O}(\log_2n) = \mathcal{O}(n\log_2n) = \mathcal{O}(n\sqrt n),$$
wenn man zum Sortieren ein schnelles Verfahren in $\mathcal{O}(n\log_2n)$ einsetzt. $\mathcal{O}(n\log_2n)\subset\mathcal{O}(n\sqrt n)$ gilt wegen $1<\log n<\sqrt n<n$. In obigem Ausdruck wurde $\log_2 n$ zur besseren Vergleichbarkeit der beiden Ausdrücke durch $\sqrt n$ ersetzt, wobei $\sqrt n > 1$ für alle $n>1$.
Vergleicht man die beiden Aufwände, nämlich $\mathcal{O}(n)$ (lineare Suche in unsortierter Liste) und den höheren $\mathcal{O}(n\sqrt n)$ (Binärsuche in sortierter Liste) miteinander, so geht die Motivation zur Sortierung der Liste rasch verloren. Jedenfalls auf den ersten Blick.
Geht man hingegen von der realistischen Situation aus, dass die Liste sehr oft ($K$-mal) durchsucht wird, wofür jedoch nur eine einzige Sortierung notwendig ist, ergeben sich amortisierte Kosten in Höhe von
$$1\cdot T_{sort}+K\cdot\mathcal{O}(\log_2 n)=K\cdot\mathcal{O}(\log_2 n)<K\cdot \mathcal{O}(n).$$
Für sehr große $K$ stellt sich der Sortieraufwand $T_{sort}$ wie eine Konstante dar und kann vernachlässigt werden. Damit erhalten wir einen Aufwand, der besser ist als der für die Suche in einer unsortierten Liste.
Beispiel 2: Dynamisches Array
Wir betrachten die Operation des Hinzufügens eines Elements in einem dynamischen Array. Obwohl dies meistens mit einem Aufwand von $\mathcal{O}(1)$ möglich ist, wird davon ausgegangen, dass die Array-Kapazität verdoppelt werden muss, was mit dem Umkopieren der vorhandenen Feldelemente und damit einem Aufwand von $\mathcal{O}(n)$ einher geht. Dadurch liegt die worst-case-Komplexität bei $\mathcal{O}(n)$, was zunächst abschreckend wirkt, denn andere Datenstrukturen können dies (selbst im worst-case) in $\mathcal{O}(1)$.
Offensichtlich erhalten wir ein präziseres Analyseergebnis, wenn wir eine Folge von Operationen (statt nur eine) und ggf. die Reihenfolge von Operationen im worst case betrachten.
Genau dies erreichen wir mit der amortisierten Analyse.
Die amortisierte Analyse berechnet die mittleren Kosten über eine Folge von Operationen, in der viele dieser Operationen billig sind und nur wenige teuer in Bezug auf deren Beitrag zur Gesamtzeit. Sie garantiert die durchschnittliche Performance jeder Operation im worst case (ohne Wahrscheinlichkeiten).
Aggregat-Methode
Wir betrachten eine Folge von $n$ (durchaus verschiedener/verschiedenartiger) Operationen und mitteln deren Gesamtausführungszeit $T(n)$, erhalten also $\frac{T(n)}{n}$. Fakt ist, dass in der betrachteten Folge der schlechteste Fall sehr selten vorkommt. Einige wenige teure Operationen sind erlaubt, während die Durchschnittskosten niedrig gehalten werden.
$$T_{amort}(n) = \frac{\text{Summe der Kosten aller $n$ Operationen der Folge}}{n}=\frac{T(n)}{n}$$
Die Summe der Zeitaufwände aller $n$ Operationen der betrachteten Operationenfolge wird durch $n$ dividiert.
Dynamisches Array
Zur Implementation des ADT Stack können dynamische Felder verwendet werden.
Bei einem dynamischen Feld wird zunächst ein Array der Größe $1$ initialisiert. Immer dann, wenn die Feldgröße erschöpft ist, d.h. push auf letzten freien Platz, wird per resize ein neues Array mit doppelter Länge erstellt. Die Elemente des ursprünglichen Feldes werden in das neue hineinkopiert. Sollte dieses Array nicht mehr ausreichen, so wird es durch ein neues doppelter Länge ersetzt usw.
Die push-Operation "Einfügen eines Elements in ein Array" wird also sehr oft mit $\mathcal{O}(1)$ zu bewerkstelligen sein und nur sehr selten $\mathcal{O}(n)$ für die push- mit resize-Operation erfordern.
Wir betrachten eine Folge von push-Operationen ggf. mit resize auf einer anfangs leeren Datenstruktur. Nach dem ersten push findet eine Verdopplung der Feldgröße auf 2 statt, nach dem zweiten push ebenso. Nun stehen 4 Plätze zur Verfügung, sodass nach der dritten push-Operation kein resize ausgeführt wird, wohl aber nach der vierten. Das jeweils aktuelle $n$ gibt die zugehörige Anzahl der Feldelemente an, so dass die ggf. stattfindende resize-Operation mit $\mathcal{O}(n)$ arbeitet.
| n | push ohne resize | resize | Feldzugriffe | Feldzugriffe (kumulativ) |
|---|---|---|---|---|
| 1 | 1 | 1 | 2 | 2 |
| 2 | 1 | 2 | 3 | 5 |
| 3 | 1 | 0 | 1 | 6 |
| 4 | 1 | 4 | 5 | 11 |
| 5 | 1 | 0 | 1 | 12 |
| 6 | 1 | 0 | 1 | 13 |
| 7 | 1 | 0 | 1 | 14 |
| 8 | 1 | 8 | 9 | 23 |
| 9 | 1 | 0 | 1 | 24 |
| : | 1 | 0 | 1 | : |
| 15 | 1 | 0 | 1 | 30 |
| 16 | 1 | 16 | 17 | 47 |
| : | : | : | : | : |
Aus der Tabelle geht hervor, dass für beliebiges $n$ wenigstens eine push-Operation ohne resize stattfindet. Dafür veranschlagen wir einen Aufwand in Höhe von $n\cdot\mathcal{O}(1)=\mathcal{O}(n).$
Ist $n$ eine Zweierpotenz, kommen $1+2+4+8+16+\ldots+n$ resize-Operationen hinzu. Für $n=16$ bedeutet das (s. Tabelle, 3. Spalte): $1+2+4+8+16=31$ (was dann mit den $16$ push-Operationen $31+16=47$ ergibt) und allgemein: $$\sum_{i=0}^{\log_2n}2^i = 2^{\log_2n+1}-1 = 2\cdot2^{\log_2n}-1 = 2n-1,$$ denn es ist eine endliche geometrische Reihe mit $q=2$.
Dies ergibt insgesamt $T(n)=n+2n-1=3n-1$, was man an den Tabellenwerten (letzte Spalte von links) für Zweierpotenzen sehr gut überprüfen kann.
$$T_{amort}(n) = \frac{T(n)}{n} = \frac{\mathcal{O}(n)}{n} = \mathcal{O}(1)$$
Damit ergeben sich für die Insert-Opertion bei einem dynamischen Array amortisierte Kosten von $\mathcal{O}(1)$.
Binärzähler
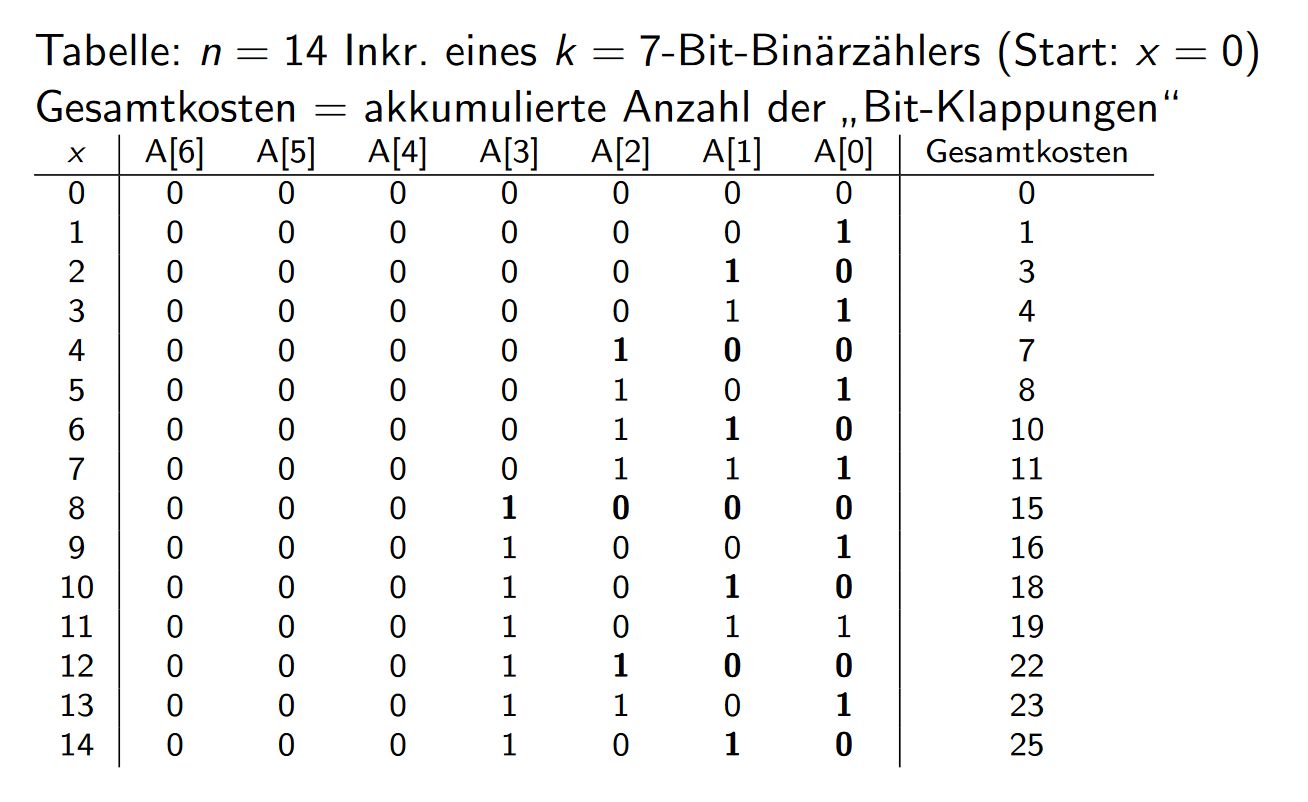
Situation: $n$ Inkrementierungen eines $k$-Bit-Binärzählers ($k=\log_2n$) mit Anfangswert $0$, siehe auch HPI teaching.
Array: $A[0 \dotsc k-1],\ A[i] \in \{0,1\},$
$$x = \sum_{i=0}^{k-1} A[i] \cdot 2^i$$
Aufwand: akkumulierte Anzahl der "Bit-Klappungen"
Worst case: Alle $k$ Bits werden invertiert, da sie von 1 auf 0 wechseln. Dies ist beim Übergang von $2^i - 1$ zu $2^i$ der Fall. Folglich beträgt der Aufwand je Inkrementierungsschritt im schlechtesten Fall $\mathcal{O}(k) = \mathcal{O}(\log_2n)$. Dies ist zwar korrekt, aber zu grob.
Die Tabelle zeigt, wann ein Bit invertiert werden muss. In diesem Fall steht eine 1 an dem entsprechenden Index. Man kann beobachten, dass $A[0]$ $n$-mal invertiert wird, $A[1]$ wird in jedem zweiten Schritt invertiert, also $\frac{n}{2}$-mal, $A[2]$ in jedem vierten Schritt, d.h. $\frac{n}{4}$-mal. Verallgemeinert kann man sagen, dass $A[i]$ $\frac{n}{2^i}$-mal, mit $i\geq 0$, invertiert werden muss. Für die Gesamtkosten ergibt sich also:
$$T_{\text{gesamt}}(n) = \sum_{i=0}^{k-1} \frac{n}{2^i} = n \cdot \sum_{i=0}^{k-1} \frac{1}{2^i} < n \cdot \sum_{i=0}^{\infty} \frac{1}{2^i} = 2n \in \mathcal{O}(n)$$
$$T(n) = \frac{\mathcal{O}(n)}{n} \in \mathcal{O}(1)$$
Es ergibt sich also ein amortisierter Aufwand von $\mathcal{O}(1)$ für die Inkrement-Operation.
Die Aggregat-Methode ist die einfachste Methode zur amortisierten Analyse, jedoch lassen sich komplexere Algorithmen mit ihr nicht analysieren.
Stackoperationen
Wir betrachten die Stackoperationen push(S,x) und pop(S), die ein Element `x` auf den Stapel `S` legt bzw. das oberste Stapelement (top of stack) vom Stapel `S` entfernt und zurückgibt.
Die Kosten je einer `push`- bzw. `pop`-Operation betragen $\mathcal{O}(1)$, für eine Folge mit $n$ dieser Operationen ergeben sich Gesamtkosten i.H.v. $\mathcal{O}(n)$. Dabei ist klar, dass eine `pop`-Operation nur dann ausgeführt werden darf, wenn der Stapel nicht leer ist (`S`$\not=\emptyset$).
Wir fügen eine Operation `multipop(S,k)` hinzu, die die obersten $k$ Elemente des Stapels `S` entfernt. Falls `S` weniger als $k$ Elemente enthält, wird der gesamte Stapelinhalt entfernt.
Zur Implementation von `multipop` benötigen wir `stack-empty?` mit folgender Definition:
$$\textrm{stack-empty?(S)} = \left\{ \begin{array}{ll} w, & \textrm{wenn } S=\emptyset \\ f, & \, \textrm{sonst} \\ \end{array} \right. $$
Dann können wir `multipop` wir folgt angeben:
multipop(S,k) =
while(not(stack-empty?(S)) and k != 0)
do pop(S); k=k-1
Sei $s$ die aktuelle Anzahl der Elemente auf dem Stapel `S`. Dann ist $\min(s,k)$ die Anzahl der `while`-Schleifen. Dies entspricht der Anzahl der `pop`-Operationen mit jeweils $\mathcal{O}(1)$. Der worst-case-Aufwand dafür ergibt sich aus
$$\mathcal{O}(\mathcal{O}(1)\cdot\min(s,k)) = \mathcal{O}(1\cdot\min(s,k)) = \mathcal{O}(s).$$
Wir betrachten nun insgesamt $n$ Operationen `push` und `multipop` auf einem anfangs leeren Stapel. Wenn für jedes $n$ ein `multipop` stattfinden würde, kostet das $\mathcal{O}(n^2)$ im worst case. Da aber nach einem `multipop` der Stapelinhalt verringert wurde und jedes der $n$ Elemente nur genau einmal gepopt ($\mathcal{O}(n)$) werden kann, wenn es vorher gepushed ($\mathcal{O}(n)$) wurde, ergibt sich ein amortisierter Aufwand von $\frac{\mathcal{O}(n)+\mathcal{O}(n)}{n} = \frac{\mathcal{O}(n)}{n}=\mathcal{O}(1)$ als durchschnittliche Kosten je Operation.
Accounting-Methode
Bei der Accounting-Methode gibt es ein Bankkonto, auf welches man Guthaben laden kann. Dieses Guthaben kann man sich als Münzen vorstellen, die eingezahlt werden, wenn eine Operation billig ist, d.h. mit sehr geringem Zeitaufwand ausgeführt wird. Bei Operationen mit hohen Kosten (großer Zeitaufwand) besteht die Möglichkeit, vorhandenes Guthaben vom Konto zu nehmen und damit die Operation zu "bezahlen". Der Betrag auf dem Konto darf dabei nicht negativ werden, man möchte nämlich zeigen, dass die tatsächlichen Kosten $\leqslant$ amortisierte Kosten sind.
Dynamisches Array
Hier wird folgendermaßen vorgegangen:
- wenn eine Insertion-Operation keine Verdopplung verursacht, zahlt man eine Münze mit dem Wert $\mathcal{O}(1)$ in das Konto ein. - wenn eine Insertion-Operation eine Verdopplung verursacht, so wurden seit der letzten Verdopplung $\frac{n}{2}$ Elemente eingefügt. $\frac{n}{2}$ Münzen können nun verwendet werden um die $\mathcal{O}(n)$ Operation zu bezahlen.
- amortisierte Kosten für eine Verdopplung: $\mathcal{O}(n) - c \cdot \frac{n}{2} = 0$ für ein $c$, das groß genug ist. (In dem Fall $c=2$) - da $c$ eine Konstante ist, gilt, dass die amortisierten Kosten für eine Insert-Operation $1 + c \in \mathcal{O}(1)$ sind.
Inkrementieren eines Binärzählers
Mit der Accounting-Methode wird die Anzahl der Bitwechsel bei der Inkrementation eines Binärzählers analysiert. (Quelle: Wikipedia)
Elementare Operationen sind das Setzen von einem Bit von 0 auf 1 bzw. das Setzen von einem Bit von 1 auf 0. Die realen Kosten für beide Operation werden auf eine Einheit gesetzt. Im Gegensatz dazu werden die amortisierten Kosten auf 2 bzw. 0 Einheiten gesetzt. Wenn ein Bit auf 1 gesetzt wird, entstehen zwei Einheiten amortisierte Kosten von denen nur eine verbraucht und der Rest auf das Konto eingezahlt wird. Bei dem Bit-Wechsel von 1 nach 0 muss eine Einheit amortisierte Kosten von dem Konto bezahlt werden.
Da nun bei jeder Inkrementation des Zählers genau ein Bit von 0 auf 1 gesetzt wird, enthält das Konto genug Einheiten um alle möglichen Wechsel von 1 auf 0 zu bezahlen. Also sind die amortisierten Gesamtkosten für $n$ Inkrementierungen in $\mathcal{O}(n)$ und je Operation im Durchschnitt $\mathcal{O}(1)$.
Potenzial-Methode (Potenzialfunktionsmethode)
Bei der Potenzial-Methode, bzw. beim Beweis mit Potenzialfunktion, wird eine Funktion definiert, die von einer Datenstruktur in einem bestimmten Zustand auf eine reelle nicht-negative Zahl abbildet. Diesen Wert bezeichnet man als Potenzial. Dieses Konzept ähnelt der Accounting Methode.
Definition 4.2 Es wird eine Datenstruktur zum Zeitpunkt $i$ als $D_i$ betrachtet. Zu definieren ist also eine Potenzialfunktion $\Phi : D_i \rightarrow \mathbb{R^+_0}$. Die tatsächlichen Kosten einer Operation werden $c_i$ bezeichnet. Für die amortisierten Kosten $\hat{c}_i$ ergibt sich folgende Gleichung:
$$ \hat{c}_i = c_i + \Delta \Phi(D_i) = c_i + \Phi(D_i) - \Phi(D_{i-1}) $$
Die amortisierten Kosten einer Operation sind die Summe aus den tatsächlichen Kosten dieser Operation und der Veränderung der Potenzialfunktion, die durch diese Operation verursacht wird. Die Veränderung der Potenzialfunktion ist gleich der Differenz aus $\Phi$ zum Zeitpunkt $i$ und $\Phi$ zum Zeitpunkt $i-1$.
Intuitiv kann man sagen, dass die Potenzialfunktion angeben soll, wie labil der aktuelle Zustand der Datenstruktur gegenüber teure Operationen ist, d.h. wie nah die nächste teure Operation ist.
Aus der Gleichung für die amortisierten Kosten $\hat{c}_i$ lässt sich eine Gleichung für die amortisierten Kosten aller Operationen von 1 bis $n$ herleiten:
Lemma 4.3 $$ \begin{align*} \sum_{i=1}^n \hat{c}_i &= \sum_{i=1}^n c_i + \sum_{i=1}^n (\Phi(D_i) - \Phi(D_{i-1})) \\ &= \sum_{i=1}^n c_i + (\Phi(D_1) - \Phi(D_0) + \Phi(D_2) - \Phi(D_1) + \dotsc + \Phi(D_n) - \Phi(D_{n-1})) \\ \end{align*} $$
Bei der Teleskopsumme $\sum \Phi(D_i) - \Phi(D_{i-1})$ kürzen sich alle Terme außer $\Phi(D_n)$ und $\Phi(D_0)$. Somit ergibt sich:
Korollar 4.4 $$ \begin{align*} \sum_{i=1}^n \hat{c}_i &= \sum_{i=1}^n c_i + \Phi(D_n) - \Phi(D_0) \\ \sum \text{amortisierte Kosten} &= \sum \text{tatsächliche Kosten} + \Phi(\text{finale Datenstruktur}) - \Phi(\text{initiale Datenstruktur}) \end{align*} $$
Dynamische Arrays
Bei dynamischen Arrays, deren Größe sich verdoppelt, wenn sie voll sind, lässt sich beispielsweise folgende Potenzialfunktion aufstellen:
$$ \Phi(D_i) = 2n-m $$
$n$ ist dabei die Anzahl der eigentlichen Elemente im dynamischen Array und $m$ ist die Anzahl der allozierten Speicherplätze. Direkt nach einer Verdopplungsoperation ist die Hälfte der Speicherplätze mit Elementen gefüllt, also $n = \frac{m}{2}$. Damit ist
$$ \Phi(D_i) = 2n-m = 2 \cdot \frac{m}{2} - m = 0 $$
$\Phi(D_i) = 0$ bedeutet, dass die Datenstruktur weit entfernt von der nächsten tueren Operation ist. Kurz vor der Verdopplungsoperation beträgt $n = m$, also ist
$$ \Phi(D_i) = 2n - m = 2m - m = m $$
Nun kann sowohl für die billige, als auch für die teure Operation bewiesen werden, dass die amortisierten Kosten in beiden Fällen $\mathcal{O}(1)$ betragen.
Pushback Operation ohne Speicherallokation
$$ \begin{align*} \hat{c}_i &= c_i + \Delta \Phi(D_i) \\ &= c_i + \Phi(D_i) - \Phi(D_{i-1}) \\ &= 1 + 2(n+1) - m - (2n - m) \\ &= 1 + 2 \\ &= 3 \\ &\in \mathcal{O}(1) \end{align*} $$
Pushback Operation mit Speicherallokation
In diesem Fall ist das momentane Array voll und es gilt $n = m$:
$$ \begin{align*} \hat{c}_i &= c_i + \Delta \Phi(D_i) \\ &= c_i + \Phi(D_i) - \Phi(D_{i-1}) \\ &= n + 1 + 2(n + 1) - 2m - (2n - m) \\ &= n + 1 + 2 - m \\ &= n + 1 + 2 - n \\ &= 3 \\ &\in \mathcal{O}(1) \end{align*} $$
Binärzähler
Beim Binärzahler könnte man zunächst intuitiv die Anzahl der hinterneinander folgenden Bits, die 1 sind, von hinten, als Potenzialfunktion nehmen. Demnach hätte 01001000 eine kleines Potenzial, ist also weit weg von teuren Operationen, 01111111 hätte demnach ein großes Potenzial, was auch zu stimmen scheint, da die nächste Operation zeitaufwendig sein wird. Betrachtet man aber beispielsweise 11111110, so wäre das Potenzial 0. Eine teure Operation ist also vermeindlich weit entfernt. Jedoch wird die übernächste Operation teuer. Die Anzahl der hinterneinander folgenden 1-Bits von hinten, scheint also keine passende Potenzialfuktion zu sein.
Stattdessen ist die Gesamtzahl der 1-Bits der Binärzahl aussagekräftiger. Man spricht auch vom Hamming-Gewicht (hamming weight) der Binärzahl.
$\text{hamming_weight}(01001000) = 2$, $\text{hamming_weight}(01111111) = 7$, $\text{hamming_weight}(11111110) = 7$.
Definition 4.5 Das Hamming-Gewicht einer Zeichenkette ist die Anzahl der vom Nullzeichen des verwendeten Alphabets verschiedenen Zeichen.
Auch hier kann gezeigt werden, dass die amortisierten Kosten für eine Inkrementoperation $\mathcal{O}(1)$ sind.
$$ \hat{c}_i = c_i + \Delta \Phi(D_i) $$
Bei einem Inkrement einer Binärzahl werden alle aufeinanderfolgenden Bits, die 1 sind, zu 0 invertiert und das erste Bit von rechts, das 0 ist, wird zu 1 invertiert. Damit ergeben sich folgende Kosten $c$ für eine Binärzahl mit $t$ aufeinnanderfolgenden 1-Bits von hinten: $c = t + 1$
$$ \begin{align*} \hat{c}_i &= t + 1 + \Delta \Phi(D_i) \\ &= t + 1 + \Phi(D_i) - \Phi(D_{i-1}) \\ \end{align*} $$
Das Potenzial $\Phi(D_{i-1})$ vor der Inkrementoperation ist $\text{hamming_weight}(b)$. Durch die Inkrementoperation werden $t$ aufeinanderfolgende 1-Bits zu 0, wodurch sich das Hamming-Gewicht um $t$ verkleinert. Das erste 0-Bit von hinten wird zu 1, dadurch vergrößert sich das Hamming-Gewicht um 1. Das Potenzial $\Phi(D_i)$ nach der Inkrementoperation beträgt demnach $\text{hamming_weight}(b) - t + 1$.
$$ \begin{align*} \hat{c}_i &= t + 1 + \Delta \Phi(D_i) \\ &= t + 1 + (\text{hamming_weight}(b) - t + 1) - (\text{hamming_weight}(b)) \\ &= t + 1 - t + 1 \\ &= 2 \\ &\in \mathcal{O}(1) \end{align*} $$