Asymptotische Aufwandsordnungen
Aus ProgrammingWiki
Inhaltsverzeichnis |
Bit-Komplexität
Im Gegensatz zum uniformen Komplexitätsmaß (Registermaschine) betrachten wir im Allgemeinen die Bit-Komplexität (Turingmaschine, siehe Modul "Theoretische Informatik"). In der Berechenbarkeitstheorie werden die zugehörigen Maschinenmodelle behandelt. Bei der Bit-Komplexität werden die Problemgrößen durch die Stelligkeit der verwendeten Eingaben bestimmt.
Wie eine einfache Rechnung zeigt, spielt die Wahl der Zahlenbasis dabei keine Rolle, da sie die Stelligkeit einer natürlichen Zahl lediglich durch einen konstanten Faktor verändert.
Für eine höchstens $m$-stellige natürliche Zahl $n$ im $10$er System, gilt $n\leq 10^{m}-1$. Für eine höchstens $p$-stellige Dualzahl $n$ gilt $n\leq 2^p-1$. Aus $2^p-1=10^m-1$, mit $m,p\in \mathbb{N}$ und $0\leq m,p$, folgt $3m<p<4m$.
Die Stelligkeit von $n$ im Dualsystem ist also durch $4$ mal deren Stelligkeit im Dezimalsystem beschränkt. Ist $n$ höchstens 3-stellig, d.h. $n\leq 999$, so ist $n$ im Dualsystem höchstens $11$-stellig: $n=1111100111$ ($10$-stellig), s. Konverter.
Für die Bit-Komplexität wird die Eingabe im Allgemeinen als Dualzahlwort auf das Band der Turingmaschine geschrieben.
Definition und Notation
Groß-O
Die Groß-O ($\mathcal{O}$) Notation ist eine mathematische Notation, die das Verhalten einer Funktion für größer werdende Argumente beschreibt. Der sog. $\mathcal{O}$-Kalkül gehört zur Gruppe der Notationen, welche durch Paul Bachmann und Edmund Landau eingeführt wurden, und deshalb auch Bachmann-Landau Notationen genannt werden.
In der Informatik wird die Groß-O-Notation genutzt, um Algorithmen bezüglich ihrer Laufzeit und ihres Speicherbedarfs zu klassifizieren.
Anmerkung
In den folgenden Definitionen wird traditionell $f(n)$ auch dann geschrieben, wenn es sich nicht um einen Funktionswert, sondern um eine einstellige Funktion $f$ mit $n\mapsto f(n)$ handelt.
Definition 1.1
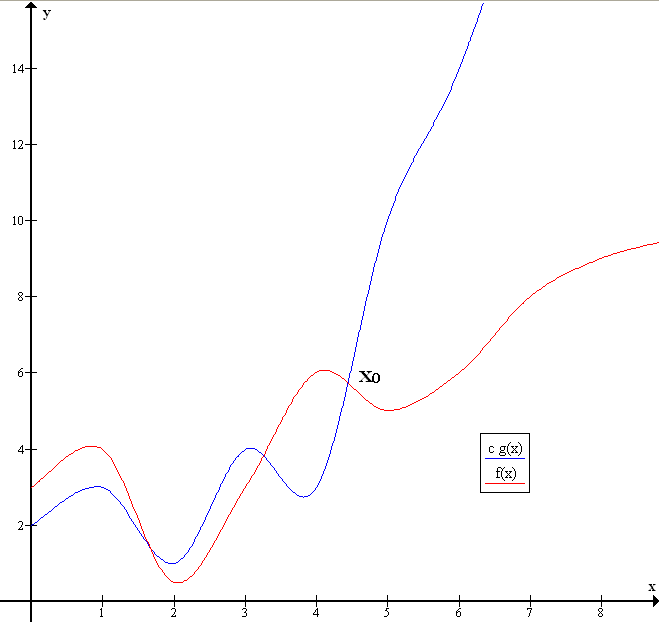
$$f(n) \in \mathcal{O}(g(n)) \text{ mit } n \rightarrow \infty \text{ genau dann, wenn}$$ $$\exists c \in \mathbb{R}^+ : \exists n_0 \in \mathbb{N} : \forall n \geqslant n_0 : f(n) \leqslant c \cdot g(n)$$
Diese Definition sagt aus, dass $f$ genau dann zur Menge $\mathcal{O}(g)$ gehört, wenn es eine positive reelle Zahl $c$ gibt, sodass alle $f(n)$ ab einem gewissen $n_0$ kleiner sind als $c \cdot g(n)$. Die Funktion $g$, welche durch die Landau-Notation angegeben wird, dient also als obere Schranke für die Funktion $f$.
Da es sich um eine obere Schranke handelt, gilt beispielsweise: $\mathcal{O}(n) \subset \mathcal{O}(n^2)$ oder $\mathcal{O}(n^2) \subset \mathcal{O}(n^3)$ oder $\mathcal{O}(n^2) \subset \mathcal{O}(2^n)$. Es ist also auch korrekt anstatt $\mathcal{O}(n)$, $\mathcal{O}(n^2)$ anzugeben, dies wäre jedoch für die Praxis nicht sehr sinnvoll.
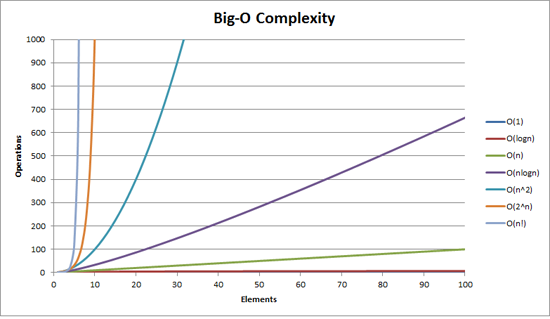
Typische Laufzeiten sind:
| Effizienzklasse | Beschreibung |
|---|---|
| $\mathcal{O}(1)$ | konstante Laufzeit (unabh. von Eingabegröße) |
| $\mathcal{O}(\log n)$ | logarithmische Laufzeit |
| $\mathcal{O}(n)$ | lineare Laufzeit, z.B. unverschachtelte Iteration |
| $\mathcal{O}(n\log n)$ | logarithmisch-lineare Laufzeit |
| $\mathcal{O}(n^c)$ | polynomiale Laufzeit (c=2: quadratisch, c=3: kubisch), z.B. verschachtelte Schleifen |
| $\mathcal{O}(c^n), c>1$ | exponentielle Laufzeit, z.B. mehrfach rekursive Funktionen |
| $\mathcal{O}(n!)$ | exponentielle Laufzeit, Stirlingsche Formel: $n!\approx\sqrt{2\pi n}\left(\frac{n}{e}\right)^n, n\rightarrow\infty$ |
Es gibt viele weitere sog. Komplexitätsklassen. Außerdem muss es sich nicht immer um die Variable $n$ handeln, es können auch mehrere Variablen innerhalb einer Komplexitätsklasse vorkommen. Zum Beispiel ist der Aufwand, um eine Wand der Höhe $h$ und der Breite $b$ zu bemalen, $\mathcal{O}(hb)$. Hier befassen wir uns jedoch nur mit Zeitaufwänden in Abhängigkeit von einer Problemgröße $n$.
Groß-Omega
Die Groß-Omega ($\Omega$) Notation ähnelt Groß-O konzeptionell, beschreibt jedoch eine untere Schranke. Die formale Defintion lautet demnach folgendermaßen:
Definition 1.2 $$f(n) \in \Omega(g(n)) \text{ mit } n \rightarrow \infty \text{ genau dann, wenn }$$ $$\exists c \in \mathbb{R}^+ : \exists n_0 \in \mathbb{N} : \forall n \geqslant n_0 : f(n) \geqslant c \cdot g(n)$$
$f$ gehört genau dann zu $\Omega(g)$, wenn es ein $c$ gibt, für das alle $f(n)$ ab einem bestimmten $n_0$ größer sind als $c \cdot g(n)$.
Groß-Theta
Im Idealfall kann man eine asymptotische Beschränkung nach oben und unten durch ein und dieselbe Funktion mit verschiedenen Faktoren angeben. Grafisch wirkt dies wie ein Band, in dem die Graphen sämtlicher Funktionen aus $\Theta(g)$ verlaufen. $\Theta$ beschreibt damit die exakte Komplexitätsklasse.
Definition 1.3 $$f(n) \in \Theta(g(n)) \text{ mit } n \rightarrow \infty \text{ genau dann, wenn }$$ $$\exists c_1, c_2 \in \mathbb{R}^+ : \exists n_0 \in \mathbb{N} : \forall n \geqslant n_0 : c_1 \cdot g(n) \leqslant f(n) \leqslant c_2 \cdot g(n)$$
bzw.
$$f(n) \in \Theta(g(n)) \text{ mit } n \rightarrow \infty \text{ genau dann, wenn }$$ $$f(n) \in \mathcal{O}(g(n)) \text{ und } f(n) \in \Omega(g(n))$$
Klein-O
Die Klein-O ($\mathcal{o}$) Notation gibt wie die Groß-O Notation eine obere Schranke an. Jedoch handelt es sich hierbei um eine strikte obere Schranke, d.h. für alle Konstanten $c$ ist die Funktion asymptotisch nach oben beschränkt, also ergibt sich folgende Definition:
Definition 1.4 $$f(n) \in \mathcal{o}(g(n)) \text{ mit } n \rightarrow \infty \text{ genau dann, wenn }$$ $$\forall c \in \mathbb{R}^+ : \exists n_0 \in \mathbb{N} : \forall n \geqslant n_0 : f(n) < c \cdot g(n)$$
Dies hat zur Folge, dass $n^2 \notin \mathcal{o}(n^2)$, aber $n^2 \in \mathcal{o}(n^3)$.
Klein-Omega
Analog ist die Klein-Omega ($\omega$) Notation eine striktere Schranke als $\Theta$. Folgende Definition ergibt sich:
Definition 1.5 $$f(n) \in \omega(g(n)) \text{ mit } n \rightarrow \infty \text{ genau dann, wenn }$$ $$\forall c \in \mathbb{R}^+ : \exists n_0 \in \mathbb{N} : \forall n \geqslant n_0 : f(n) > c \cdot g(n)$$
Auch hier muss die Ungleichung für alle $c \in \mathbb{R}^+$ gelten. Dies hat zur Folge, dass $n^2 \notin \omega(n^2)$, aber $n^2 \in \mathcal{o}(n)$ oder $n^2 \in \mathcal{o}(n \log n)$.
Anmerkung
In der Praxis wird meistens die $\mathcal{O}$-Notation verwendet.
Definition über Grenzwerte
Es ist auch möglich den Zusammenhang zweier Funktionen bezüglich der Landau-Notationen über den Grenzwert des Quotienten der beiden Funktionen zu definieren.
Definition 1.6 $$f(n) \in \mathcal{O}(g(n)) \text{ mit } n \rightarrow \infty \text{ genau dann, wenn }$$ $$0 \leqslant \lim_{n \to \infty} \frac{f(n)}{g(n)} < \infty$$
Existiert ein Grenzwert, so steigt $f(n)$ asymptotisch höchstens so stark wie $g(n)$. (Wenn es keinen Grenzwert gibt: $\lim\sup_{n\to\infty}\frac{f(n)}{g(n)}.$)
Definition 1.7 $$f(n) \in \Omega(g(n)) \text{ mit } n \rightarrow \infty \text{ genau dann, wenn }$$ $$0 < \lim_{n \to \infty} \frac{f(n)}{g(n)}$$
Ist der Grenzwert größer als 0, so steigt $f(n)$ asymptotisch mindestens so stark wie $g(n)$.
Definition 1.8 $$f(n) \in \Theta(g(n)) \text{ mit } n \rightarrow \infty \text{ genau dann, wenn }$$ $$0 < \lim_{n \to \infty} \frac{f(n)}{g(n)} < \infty$$
Gibt es einen Grenzwert größer als 0, so steigt $f(n)$ asymptotisch genauso stark wie $g(n)$.
Definition 1.9 $$f(n) \in \mathcal{o}(g(n)) \text{ mit } n \rightarrow \infty \text{ genau dann, wenn }$$ $$\lim_{n \to \infty} \frac{f(n)}{g(n)} = 0$$
Ist der Grenzwert 0, so steigt $f(n)$ asymptotisch weniger stark als $g(n)$.
Definition 1.10 $$f(n) \in \omega(g(n)) \text{ mit } n \rightarrow \infty \text{ genau dann, wenn }$$ $$\lim_{n \to \infty} \frac{f(n)}{g(n)} = \infty$$
Ist $\frac{f(n)}{g(n)}$ divergent ($\infty$) für $n\to\infty$, so steigt $f(n)$ asymptotisch stärker als $g(n)$.
Best Case, Worst Case, Average Case
Die Groß-O ($\mathcal{O}$) Notation wird verwendet, um das Laufzeitverhalten eines Algorithmus zu charakterisieren. Hierfür kommen die folgenden drei Analyseformen in Betracht: worst case, average case und best case.
Sie unterscheiden sich in der Wahl der jeweiligen Laufzeit $f(n)$ aus einer Liste von $k$ Laufzeiten $\underbrace{f(n),f(n),\ldots,f(n)}_{k\ Stück}$ für eine bestimmte Problemgröße $n$: Greift man bei einer solchen empirischen Analyse für jedes $n$ den kleinsten der $k$ Werte für $f(n)$ heraus, führt dies zu einer Best-Case-Analyse. Bildet man das arithmetische Mittel aus den jeweils $k$ Werten für $f(n)$, gelangt man zum Average-Case. Nimmt man die jeweiligen Maximalwerte, ergibt das den Worst-Case. In den genannten drei Analyseformen steht am Ende eine den Zusammenhang zwischen $n$ und Zeitaufwand $T=f(n)$ beschreibende Funktion $f$, deren asymptotische Ordnung das gesuchte Ergebnis beschreibt.
Alle drei Analyseformen sind entweder Kern einer empirischen Analyse (Datenerhebung) oder verwenden Wahrscheinlichkeiten und erfordern den Einsatz statistischer Methoden.
Wir illustrieren die drei Fälle am Beispiel von Monkey sort, auch Bogosort, stupid sort, slowsort, permutaion sort oder shotgun sort genannt. Es handelt sich um eines der ineffektivsten Sortierverfahren, das man sich ausdenken kann.
Nehmen wir an, eine Liste mit $n$ natürlichen Zahlen soll aufsteigend sortiert werden. Dann kann man folgendes Verfahren anwenden:
- Falls die Liste bereits sortiert ist, dann STOPP.
- Anderenfalls bringe die Liste durcheinander und gehe zu 1.
Best Case
Mit der Best-Case-Laufzeit wird die kürzeste Laufzeit angegeben. Sie tritt ein, wenn die zu lösende Instanz des Problems der Größe $n$ im Hinblick auf den Sortier(zeit)aufwand am günstigsten ist. Bei Monkey sort ist dies der Fall, wenn die Liste mit den zu sortierenden Elementen bereits sortiert ist. Hierfür müsste lediglich genau einmal durch das Array traversiert werden, was einen Aufwand in $\mathcal{O}(n)$ erfordert. Da der Best-Case in der Praxis so gut wie nie auftritt, ist dessen Angabe nicht von großem Interesse.
Worst Case
Die Worst-Case-Laufzeit ist hingegen wesentlich bedeutender: Sie gibt an, wie groß die Laufzeit des Algorithmus maximal werden kann, auch wenn die betrachtete Probleminstanz noch so ungünstig ist. Bei Monkey sort tritt der Worst-Case ein, wenn alle $n!$ verschiedenen Anordnungen der Listenelemente mindestens einmal überprüft werden, ob sie aufsteigend sortiert vorliegen. Der Aufwand liegt dann in $\mathcal{O}(n\cdot n!)$, kurz: $\mathcal{O}(n!)$. Dies gilt jedoch nur dann, wenn das Verfahren überhaupt terminiert.
Average Case
Nicht immer ist die Worst-Case-Angabe hilfreich. Was ist, wenn der Worst-Case zwar bezüglich der Laufzeit sehr ungünstig ist, jedoch nur sehr selten eintritt? Hier ist die Angabe der Laufzeit im Average-Case bzw. Expected-Case repräsentativer. Eine Alternative stellt die amortisierte Analyse dar.
Bei Monkey Sort handelt es sich um einen Las-Vegas-Algorithmus, für den man einen Aufwand in $\mathcal{O}(n!)$ berechnen kann. Sowohl im Worst- als auch im Average-Case arbeitet das Verfahren mit exponentiellem Aufwand.
Vernachlässigung von Konstanten
Bei Angabe der Komplexitätsklasse unter Verwendung der $\mathcal{O}$-Notation werden konstante Summanden und konstante Faktoren vernachlässigt. Eine Laufzeit in $\mathcal{O}(2n)$ liegt tatsächlich in $\mathcal{O}(n)$. Zum einen wird dies getan, da nur die Komplexitätsklasse interessiert. Zum anderen wäre eine Angabe als $\mathcal{O}(2n)$ keineswegs genauer, wie folgende Beispiele zeigen:
Man könnte nun auf die Idee kommen, für das erste Beispiel $\mathcal{O}(n)$ und für das zweite Beispiel $\mathcal{O}(2n)$ anzugeben, da es beim ersten Beispiel eine Schleife mit $n$ Iterationen gibt und im zweiten zwei Schleifen mit $n$ Iterationen. Tatsächlich werden aber in beiden Beispielen gleich viele Operationen durchgeführt und eine Unterscheidung der Laufzeit würde hier keinen Sinn ergeben und zu falschen Schlüssen führen.
Beispiel für logarithmische Komplexität
Wir betrachten ein Beispielprogramm zur Umwandlung einer natürlichen Zahl in eine Zeichenkette.
Die Anzahl der Zyklendurchläufe beträgt $k=\log_{10}i$, denn aus $\frac{i}{10^k}=1$ folgt $i=10^k$ und damit $k=\log_{10}i$. Geht man von einem konstanten Aufwand in $\mathcal{O}(1)$ für die Operationen innerhalb der Schleife aus, so ergibt sich für $k$ Durchläufe ein Gesamtaufwand in $\mathcal{O}(\log i)$.
Übungsaufgabe
Bei der Umformung mathematischer Ausdrücke mit $\log$ kann ein Basiswechsel (von $a$ zu $b$) sehr hilfreich sein. Zeigen Sie, dass $$ a^x = b^{x\ \log_ba}.$$
Lösung
Nach der Definition des Logarithmus' ergibt sich $y$ in $p=b^y$ aus $y=\log_b{p}$, sodass $p=b^{\log_b p}$.
Setzt man $p=a^x$, so erhalten wir $a^x=b^{\log_b a^x}=b^{x\ \log_ba}$.
Man kann nun diese Gleichheit einsetzen, um beispielsweise einen Basiswechsel zu $e$ zu erzielen:
$$ \begin{align*} a^x&=b^{x\ \log_b a} \\ x^r &= e^{r \ln x} \end{align*} $$
Genau diese Beziehung für $x^r$ wird in einem Beweis weiter unten benötigt.
Polynomial vs. Exponentiell
Alle Komplexitätsklassen gehören einer der beiden (fundamental unterschiedlichen) Aufwandsordnungen an: solche mit polynomialem und solche mit exponentiellem Aufwand.
Definition
Lässt sich der Aufwand als Polynom in $n$ ausdrücken, so handelt es sich um polynomialen Aufwand. Ein Polynom hat folgende Form:
$$T(n) = \sum_{i=0}^r \left(a_i n^i\right) = a_r n^r + a_{r-1} n^{r-1} + \dotsc + a_1 n + a_0$$
$$\text{mit } r \in \mathbb{N}, a_0, \dotsc, a_r \in \mathbb{R}, a_r \neq 0$$
Es kommt vor, dass Aufwände Wurzelausdrücke enthalten. Der folgende Satz stellt sicher, dass solche pseudopolynomiale Aufwände zu den polynominalen (nicht etwas den exponentiellen) hinzugerechnet werden dürfen. Da Logarithmus- und Wurzel-Funktionen, bzw. Funktionen mit nicht-ganzzahligen Exponenten, durch Polynome nach oben beschränkt werden können, zählen diese Funktionen auch zu den Polynomialfunktionen. Beispielsweise gilt $1<\log n<\sqrt n<n$. Im Übrigen sind diese Ungleichungen bei entsprechenden Abschätzungen sehr hilfreich.
Satz
Für $n\in\mathbb{N}, n>a, a\in\mathbb{N}\text{ gilt: } \log_bn < \sqrt{n}.$
Beweis: Der Beweis erfordert einen Satz, den man als Racetrack principle (Rennbahn-Prinzip) bezeichnet. Es beschreibt das Wachstum zweier Funktionen mit Bezug auf deren Ableitungen. Diesen wichtigen Satz und dessen Beweis schieben wir im Folgenden ein.
Satz: Wenn $f'(n)>g'(n)$ für alle $n>a$ und $f(a)=g(a)$, dann gilt $f(n)>g(n)$ für alle $n>a$.
Die sehr anschauliche Fassung lautet:
“This principle is derived from the fact that if a horse named Frank Fleetfeet always runs faster than a horse named Greg Gooseleg, then if Frank and Greg start a race from the same place and the same time, then Frank will win. More briefly, the horse that starts fast and stays fast wins.” (Quelle: Wikipedia)
Beweis: Sei $h(n)=f(n)-g(n)$. Wegen $f'(x)>g'(x)$ gilt $h'(n)=f'(n)-g'(n)>0$ für alle $n>a$. Wegen $f(a)=g(a)$ gilt außerdem $h(a)=f(a)-g(a)=0$.
Nach dem Mittelwertsatz der Differenzialrechnung gibt es wenigstens ein $x\in[a,n]$ mit $x>a$, so dass $h'(x)=\frac{h(n)-h(a)}{n-a}=\frac{f(n)-g(n)}{n-a}>0$, da $h(a)=0$.
Es gilt $f(n)-g(n)>0$, d.h. $f(n)>g(n)$, für alle $n>a$.
Nun können wir uns um die obere Schranke für die Logarithmusfunktion kümmern.
Beweis:
$f(n)=\sqrt{n}=n^\frac{1}{2}$, $f'(n)=\frac{1}{2}n^{-\frac{1}{2}}=\frac{1}{2\sqrt{n}}$.
$g(n)=\log_bn=\frac{\ln n}{\ln b}$, $g'(n)=\frac{1}{\ln b}\cdot\frac{1}{n}$
z.z.: $f(n)>g(n)\text{ für alle } n>a.$
Um das Racetrack principle anwenden zu können, müssen wir zuerst zeigen, dass es ein $a$ gibt, sodass $f'(n)>g'(n)$ für alle $n>a$:
$\frac{1}{2\sqrt{n}}>\frac{1}{n\ln{b}}$ Das ist der Fall, wenn
$\lim_{n\to\infty}\frac{2\sqrt{n}}{n\ln{b}} = \lim_{n\to\infty}\frac{2}{\ln{b}\sqrt{n}} = 0$, denn der Nenner wird für unbeschränkte wachsende $n$ immer größer.
Ab welchem $a$ ist das der Fall? $$ \begin{align*} f'(a) &= g'(a)\\ \frac{1}{2\sqrt{a}} &= \frac{1}{a\ln{b}}\\ 2\sqrt{a} &= a\ln{b}, \text{ mit } m = \sqrt{a}, a=m^2\\ 0 &= m^2\ln{b}-2m\\ 0 &= m\ln{b}-2 \\ m &= \frac{2}{\ln{b}}\\ a &= \frac{4}{(\ln{b})^2} \end{align*} $$
Für $b=e$: $a=\frac{4}{1}=4$
Für $b=2$: $a=\frac{4}{(\ln{2})^2}=8.325,\text{ d.h. } a=9$
Nun ist noch die zweite Voraussetzung für die Anwendung des Racetrack principles sicherzustellen:
$$ \begin{align*} f(a) &= g(a), \text{ z.B. für } a=9, b=2\\ \sqrt{9} &= \log_2{9}\\ 3 &= 3 \end{align*} $$
Da $f'(n) > g'(n)$ und $f(a)=g(a)$ gilt $f(n) > g(n) \text{ für alle } n>a,\text{ d.h. } \sqrt{n}>\log_b{n}.$
Definition
Lässt sich der Aufwand $T$ nicht als Polynom, sondern in der Gestalt $T(n) = c \cdot z^n$, mit $c, z \in \mathbb{R}$, $c \neq 0$ und $z > 1$, angeben, so spricht man von exponentiellem Aufwand.
Für die Praxis ist diese Einteilung entscheidend, da man Algorithmen mit exponentiellen Aufwand schon für relativ kleine und erst recht für größere $n$ als nicht praktikabel einstufen muss. Bei Algorithmen mit exponentiellem Zeitaufwand steigt die benötigte Zeit mit größer werdenden $n$ so gigantisch an, dass man in der Größenordnung von Jahrmillionen auf das Ergebnis warten müsste, sodass der Algorithmus nutzlos ist.
Um dies zu verdeutlichen, vergleichen wir die Dauer der Berechnungen bei $T_1(n) = 10000 \cdot n^2$ und $T_2(n) = 2^n$, unter der Annahme, dass der Computer $10^9$ Operationen in der Sekunde ausführt.
T1(n) T2(n) 5 0.00025s 0.0s 10 0.001s 0.0s 15 0.00225s 3e-05s 20 0.004s 0.00105s 25 0.00625s 0.03355s 30 0.009s 1.07374s 35 0.01225s 34.35974s 40 0.016s 18.32519min 45 0.02025s 9.77344h 50 0.025s 13d 55 0.03025s 1yrs 60 0.036s 36yrs 65 0.04225s 1,169yrs 70 0.049s 37,436yrs 75 0.05625s 1,197,962yrs 80 0.064s 38,334,786yrs 85 0.07225s 1,226,713,160yrs 90 0.081s 39,254,821,134yrs 95 0.09025s 1,256,154,276,291yrs 100 0.1s 40,196,936,841,331yrs
Während $T2$ für sehr kleine Werte günstigere Laufzeiten liefert als $T1$, was zunächst nicht auf einen großen Anstieg der Laufzeit schließen lässt, wird doch relativ schnell klar, wie langsam ein Algorithmus mit $T2$ ist. Bereits für $n=100$ werden über 40 Billionen Jahre Rechenzeit benötigt.
Satz: Jede Exponentialfunktion, repräsentiert durch $f(x) = e^x$, wächst schneller als jede Polynomfunktion $g(x) = x^r$ mit $x,r \in \mathbb{N}, r>0$ für $x \to \infty$.
Beweis: $$\text{z.z. } \lim_{x\to\infty}\frac{x^r}{e^x}=0\text{ mit } x,r \in \mathbb{N}, r>0$$
$$\lim_{x\to\infty}\frac{x^r}{e^x} = \lim_{x\to\infty}\frac{e^{r\ln x}}{e^x} = \lim_{x\to\infty} e^{r\ln x - x} = \lim_{x\to\infty}\frac{1}{e^{x-r\ln x}} = 0,\text{ unter Verwendung von }x^r = e^{r \ln x},\text{ von oben.}$$
Wegen $\ln x < \sqrt x < x$ gilt $x-r\sqrt x \to\infty$ für große $x$.
Übungsaufgabe
Beweisen Sie folgenden Satz unter Verwendung der Regel von l'Hospital.
Satz: Jede Exponentialfunktion $f(n) = a^n$ mit $a > 1$ für $n \to \infty$ wächst schneller als jede Polynomfunktion $g(n) = b \cdot n^c$ mit $c \in \mathbb{N}$ für $n \to \infty$.
Lösung
Beweis:
$$\text{Behauptung: } a^n \in \omega(b \cdot n^c)$$ $$a^n \in \omega(b \cdot n^c) \implies \lim_{n \to \infty} \frac{a^n}{b \cdot n^c} = \infty$$
$$\lim_{n \to \infty} \frac{a^n}{b \cdot n^c} = \lim_{n \to \infty} \frac{\mathrm{e}^{\ln(a) \cdot n}}{b \cdot n^c} = \lim_{n \to \infty} \frac{\frac{1}{b \cdot n^c}}{\frac{1}{\mathrm{e}^{\ln(a) \cdot n}}}$$
Da hier sowohl Zähler als auch Nenner gegen 0 streben, kann die Regel von l'Hospital angewandt werden:
$$= \lim_{n \to \infty} \frac{\frac{d}{d n} \left(\frac{1}{b \cdot n^c} \right)}{\frac{d}{d n} \left(\frac{1}{\mathrm{e}^{\ln(a) \cdot n}}\right)} = \lim_{n \to \infty} \frac{\frac{1}{\frac{d}{d n}(b \cdot n^c)}}{\frac{1}{\frac{d}{d n}(\mathrm{e}^{\ln(a) \cdot n})}} = \lim_{n \to \infty} \frac{\frac{1}{b \cdot c \cdot n^{c-1}}}{\frac{1}{\ln(a) \cdot a^n}} $$
Da weiterhin sowohl Zähler als auch Nenner gegen 0 streben, muss die Regel von l'Hospital solange angewandt werden, bis dies bei einem der beiden Terme nicht mehr der Fall ist:
$$= \lim_{n \to \infty} \frac{\frac{1}{b \cdot c!}}{\frac{1}{\ln^c(a) \cdot a^n}} = \lim_{n \to \infty} \frac{\ln^c(a) \cdot a^n}{b \cdot c!} = \infty$$
Es ist also von besonderer Bedeutung, wenn es gelingt, für einen Rechenprozess, der mit exponentiellem Zeitaufwand arbeitet, einen alternativen mit polynomialer Effizienz anzugeben.
Beispiel: Fibonacci-Zahlen (rekursiv, ohne Memoizing: $\mathcal{O}(2^n)$ und iterativ: $\mathcal{O}(n)$ im worst und average case)