Array
Aus ProgrammingWiki
Inhaltsverzeichnis |
Array
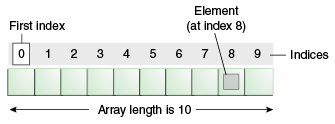
Ein Array (Feld) ist eine in den meisten Programmiersprachen anzutreffene Datenstruktur. Dabei handelt es sich um eine Sammlung von Elementen (beliebiger Typen), welche über Index identifiziert werden.
Die einfachste Form eines Arrays ist ein ein-dimensionales Array. Bei einem ein-dimensionalen Array werden alle Elemente (wenigstens konzeptionell) direkt nacheinander im Arbeitsspeicher abgelegt. Durch diese Festlegung ist es möglich, anhand des Index und der Basisadresse des Arrays (der Adresse des 0. Elements) direkt auf die Speicheradresse des Elements mit entsprechendem Index zuzugreifen.
Bei höher-dimensionalen Arrays spricht man auch von Matrizen. Hier bedarf es spezieller Funktionen, die von einem $n$-Tupel, das den Index angibt (bsp. (1, 2)), auf eine Speicheradresse abbildet. Eine mögliche Implementation für ein 2-dimensionales Array besteht darin, jede Reihe der Matrix hintereinander abzuspeichern und anhand der Länge jeder Reihe auf den entsprechenden 2-dimensionalen Index zugreifen zu können.
Es ist zu beachten, dass die Länge eines Arrays, im Gegensatz zu Listen, nicht variabel ist, da ein Array nicht über den für ihn zugewiesenen Speicherraum im Arbeitsspeicher hinausgehen darf.
Komplexitätsbetrachtung
Lesen (Access)
Da jeder Index einer festen Speicheradresse zugeordnet wird, kann in konstanter Zeit $\mathcal{O}(1)$ über Index auf ein bestimmtes Element zugegriffen werden.
Schreiben (Insert)
Zum Schreiben an gegebener Position (Index) muss zunächst die Speicheradresse gefunden werden. Dies geschieht in konstanter Zeit. Anschließend muss der entsprechende Wert der Arbeitsspeicheradresse geändert werden. Hierfür ergibt sich ebenfalls eine Gesamtlaufzeit von $\mathcal{O}(1)$.
Löschen (Delete)
Wenn die Elemente des Arrays nicht sortiert sind, muss das Feld mit aufsteigendem Index durchsucht werden. Im worst-case befindet sich das gesuchte Element am Ende des Feldes oder nicht im Feld: $\mathcal{O}(n)$. Außerdem muss das letzte Element des Feldes auf die Position des Index des gelöschten Elementes verschoben werden.
Suche eines Elements (Search)
Die Suche eines bestimmten Elements in einem Array entspricht der Frage nach dem Index, unter dem das Element im Feld gespeichert ist. Ein sehr schnelles Verfahren zur Bestimmung dieses Indexes ist die Binäre Suche. Sie setzt voraus, dass die Feldelemente (nach einer ausgewählten totalen Ordnungsrelation aufsteigend) sortiert sind. Hierfür ist einmalig ein Aufwand in $\mathcal{O}(n\log n)$ erforderlich. Nach der Sortierung geht man folgendermaßen vor.
Man vergleicht das gesuchte Element mit dem Element an mittlerer Feldposition. Stimmt es mit diesem Element überein, hat man den gesuchten Index gefunden und ist fertig. Ist das gesuchte Element kleiner als das in Mittelposition, geht die Suche im linken Elementfeld weiter, anderenfalls im rechten. Dies erinnert an die Art und Weise der Suche eines Eintrags in einem Lexikon (als Print-Medium).
Nach dieser Beschreibung erhält man eine rekursive Funktion wie folgt.
Es handelt sich um eine sehr effiziente Prozedur mit einem zeitlichen Aufwand in
$$ \mathcal{O}(\log_2n). $$
Dies ergibt sich aus dem fortgesetzten Halbieren des jeweiligen Feldes. Bei $n$ Elementen gibt es höchstens $\log_2n$ Halbierungen, bis das gesuchte Element - falls vorhanden - gefunden ist. Diesen Suchprozess illustriert ein Binärbaum der Tiefe $\log_2n$.
Zu beachten ist, dass der Aufwand zur Sortierung der Feldelemente hinzu gerechnet werden muss. Dieser ist allerdings nur genau einmal vor Anwendung des beschriebenen Suchverfahrens durchzuführen. Nachdem das Array sortiert vorliegt, kann jedes Elemenent ohne Neusortierung gesucht werden.
Selection Sort
Selection Sort ist einer der einfachsten Algorithmen zum Sortieren von Arrays. Man sucht zunächst nach dem kleinsten Element des Arrays und platziert es an den Anfang, d.h. an Position $0$. Danach sucht man das kleinste Element des Arrays ab einschl. Position $1$ und platziert es auf Position $1$. Dieser Vorgang wird für alle $n$ Positionen ausgeführt, wenn das Array $n$ Elemente enthält. Da es sich um ein In-place-Verfahren handelt, das keinen Zusatzspeicher benötigt, wird das jeweils ggf. gefundene kleinere Element mit dem Vergleichselement an der betrachteten Position vertauscht.
Komplexitätsbetrachtung
Für jedes der $n$ Feldelemente finden $n-1$ Vergleiche und höchstens ebensoviele Positionswechsel (Umspeicherungen) statt. Wenn wir für einen solchen Vergleich mit evtl. Umspeicherung einen konstanten Aufwand von $1$ ansetzen, ergibt sich folgender Gesamtaufwand:
$$T(n) = (n-1)+(n-2)+(n-3)+\ldots + 2 + 1 = \frac{n\cdot(n-1)}{2} \in \mathcal{O} \left(n^2 \right)$$
Damit liegt der Zeitaufwand von Selection Sort in $\mathcal{O}(n^2)$. Da dieser Algorithmus als In-place Algorithmus ausgeführt werden kann, wird kein zusätzlicher Speicher benötigt und der Speicheraufwand liegt in $\mathcal{O}(1)$.
Bubble Sort
Bei diesem Sortierverfahren wird das Array mehrmals durchlaufen. Alle $n-1$ Paare nebeneinander stehender Elemente werden miteinander verglichen. Ist es in falscher Reihenfolge, d.h. es steht ein größerer Wert vor einem kleineren, so tauschen die beiden Elemente ihre Positionen. Damit das komplette Array sortiert wird, muss es so oft durchlaufen werden, bis keine Umspeicherungen mehr nötig sind. Im best case ist lediglich genau ein ($1$) Durchlauf erforderlich und im worst case sind es $n$.
Komplexitätsbetrachtung
$T(n)$ bezeichnet den Zeitaufwand zur Bubble-Sort-Sortierung eines Feldes mit $n$ Elementen im worst case.
$$T(n) = n\cdot (n-1) \in \mathcal{O} \left(n^2 \right)$$
Damit liegt der Zeitaufwand von Bubble Sort in $\mathcal{O}(n^2)$. Da es sich wieder um ein In-place-Verfahren handelt, wird kein zusätzlicher Speicher benötigt sodass der Speicheraufwand in $\mathcal{O}(1)$ liegt.
Das folgende Programm verwendet stets $n$ Durchläufe und berücksichtigt nicht, ob sie wirklich benötigt werden. Das kann man verbessern!