QuickSort
Aus ProgrammingWiki
Inhaltsverzeichnis |
Algorithmus
Die Zweifel an einer guten Zeiteffizienz von MinSort unter den Sortieralgorithmen sind berechtigt.
Wir betrachten deshalb den nachfolgenden Algorithmus und implementieren ihn.
Beschreibung:
- Benutze das erste Element einer (numerischen) Liste als Trennelement.
- Erzeuge zwei Teillisten, deren Elemente kleiner bzw. größer als das Trennelement sind.
- Setze dieses Verfahren für jede nichtleere Teilliste fort und
- füge die sortierten Teillisten zur Gesamtliste zusammen.
Den so beschriebenen Sortieralgorithmus bezeichnet man als QuickSort (schnelles Sortieren). Er wurde 1962 von dem britischen Informatiker Sir Charles Antony Richard Hoare (* 11. Januar 1934) vorgestellt.
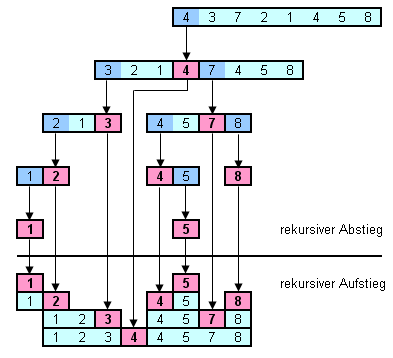
Beispiel:
Implementation:
Quelltext überprüfen:
|
Ungeordnete Zufallszahlen: |
Geordnete Zufallszahlen: |
Effizienz von QuickSort
Experimente zum Zeitaufwand
Wir wollen uns auf die empirische Analyse des Zeitaufwands von QuickSort beschränken und definieren dazu:
Die ersten Tests zeigen: QuickSort scheint deutlich effizienter als MinSort zu sein.
Wir überprüfen diese Vermutung mit den bekannten Prozeduren für Mehrfachexperimente sowie den entsprechenden grafischen Darstellungen:
Achtung! In Erwartung einer besseren Laufzeit wollen wir im Vergleich zu MinSort mit höheren Wiederholraten experimentieren.
Abschließend wollen wir die Effizienz an einer bereits sortierten Liste untersuchen. Der von uns implementierte QuickSort-Algorithmus führt dazu, dass die jeweils linke Teilliste leer bleibt. Damit werden bei gleichen Listenlängen größere Rekursionstiefen notwendig, was auch zu einem größeren Zeitaufwand führen muss.
Wir untersuchen also QuickSort im Worst-case-Fall:
Beachte: Beim Experimentieren mit dem Worst-case-Fall sind keine Wiederholungen notwendig.
Aufgaben
- Belegen Sie durch eigene empirische Untersuchungen, dass für den QuickSort-Algorithmus im Mittel gilt: $T(n) = \mathcal{O}(n \cdot \log_2 n)$
- Bestätigen Sie ebenfalls durch geeignete Untersuchungen, dass QuickSort im Worst-Case-Fall einem quadratischen Zeitaufwand unterliegt.
- Unterbreiten Sie Vorschläge, wie der Worst-Case-Fall in der Praxis weitestgehend vermieden werden kann.
Zusammenfassung
QuickSort ist ein typisches Beispiel für Teile-und-herrsche-Algorithmen (engl.: divide and conquer):
Allgemein wird ein Problem gelöst, indem man es
- in Teilprobleme zerlegt (teile - divide),
- diese Teilprobleme löst (herrsche - conquer) und
- die Teillösungen zur Gesamtlösung zusammensetzt.
Für den Quicksort-Algorithmus lassen sich folgende Abhängigkeiten und Zeitaufwandsklassen angeben:
| best case: | $T(n) = n \cdot \log_2 n$ bzw. |
| $T(n) = \mathcal{O}(n \cdot \log_2 n)$ | |
| average case: | $T(n) = 2 \cdot n \cdot \ln n \approx 1.386 \cdot n \cdot \log_2 n$ bzw. |
| $T(n) = \mathcal{O}(n \cdot \log_2 n)$ | |
| worst case: | $T(n) = \frac{n}{2} \cdot (n+1)$ bzw. |
| $T(n) = \mathcal{O}(n^2)$ |
Im Mittel ist also QuickSort deutlich effizienter als MinSort. Im ungünstigsten Fall kann es aber ebenso ineffizient werden.
Wir wollen die konkreten Funktionen zum Zeitaufwand von QuickSort vergleichend gegenüberstellen:
Zum Weiterarbeiten
MergeSort
Der Sortieralgorithmus MergeSort ist eine effiziente Alternative zum QuickSort, da sein Zeitaufwand in allen drei Fällen (best-, average-, worst-case) $T(n) = \mathcal{O}(n \cdot \log_2 n)$ beträgt. "Merge" bedeutet hier soviel wie "Zusammensetzen". Die Übersetzung mit "Sortieren durch Mischen" ist eher irreführend.
Beschreibung:
- Teile eine (numerische) Liste in zwei etwa gleich große Teillisten.
- Führe diese Teilung bei jeder Teillisten solange fort, bis nur noch einelementige Teillisten bestehen bleiben.
- Setze diese Teillisten in der richtigen Reihenfolge zur sortierten Gesamtliste zusammen.
Implementieren Sie diesen Algorithmus.
Zur Problemlösung.