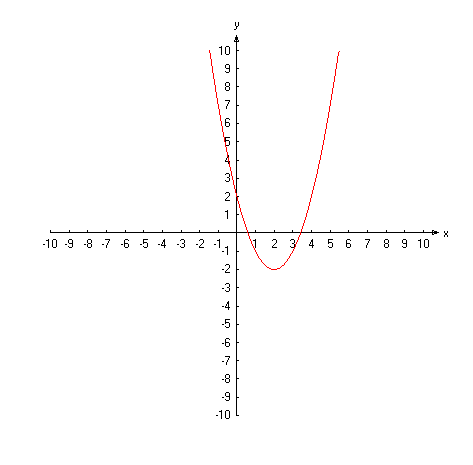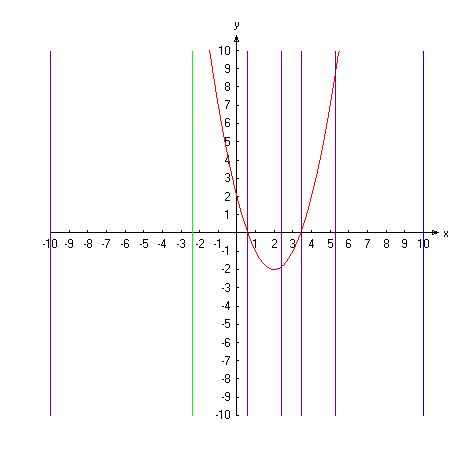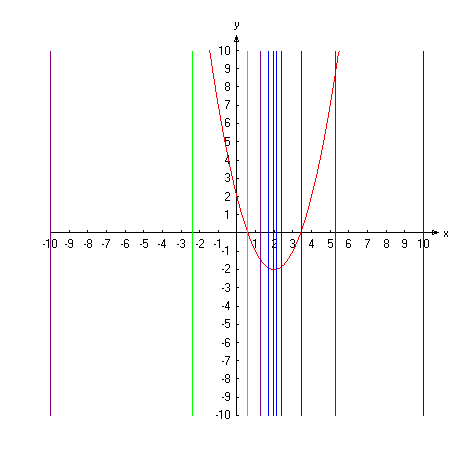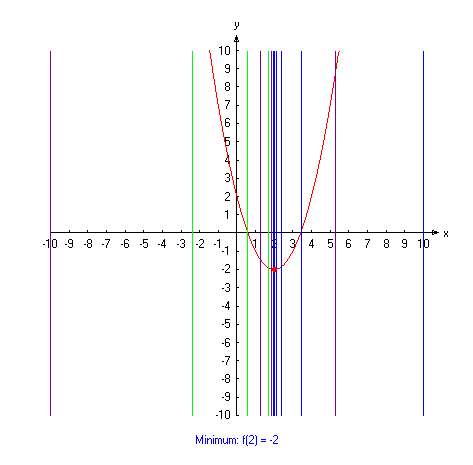Binäre Suche

Aus ProgrammingWiki

(define quotient (lambda (m n) (floor (/ m n)))) (define remainder quotient) (define numeingabe (lambda (max) (let ([eingabe (inputDialog "Deine Zahl:")]) (if (equal? eingabe 'null) #f (let ([anzahl (string->number eingabe)]) (if (or (equal? anzahl +nan.0) (< anzahl 0) (> anzahl max)) (numeingabe max) anzahl)))))) (define spielerraten (lambda (max) (letrec ([zufallszahl (lambda (max) (+ 1 (random max)))] [suche (lambda (z anzahl) (let ([zahl (numeingabe max)]) (cond [(not zahl) 'ok] [(= z zahl) (showMessage (string-append "Du hast die Zahl " (number->string zahl) " mit " (number->string anzahl) " Versuch(en) erraten!")) 'ok] [(< z zahl) (showMessage (string-append "Die Zahl " (number->string zahl) " ist zu groß!")) (suche z (+ 1 anzahl))] [else (showMessage (string-append "Die Zahl " (number->string zahl) " ist zu klein!")) (suche z (+ 1 anzahl))])))]) (suche (zufallszahl max) 1)))) (define computerraten-lsg (lambda (zahl max) (letrec ([suche (lambda (li z re) (let ([mi (floor (/ (+ li re) 2))]) (cond [(= z mi) (list z)] [(< z mi) (cons mi (suche li z mi))] [else (cons mi (suche mi z re))])))]) (suche 1 zahl (+ max 1))))) (define last (lambda (ls) (car (reverse ls)))) (define listequal? (lambda (ls1 ls2) (cond [(and (null? ls1) (null? ls2)) #t] [(or (null? ls1) (null? ls2)) #f] [(and (list? (car ls1)) (list? (car ls1))) (and (listequal? (car ls1) (car ls2)) (listequal? (cdr ls1) (cdr ls2)))] [else (and (equal? (car ls1) (car ls2)) (listequal? (cdr ls1) (cdr ls2)))])))

Inhaltsverzeichnis 1 Raten einer Zahl 2 Computerraten einer Zahl 3 Effizienz beim Raten einer Zahl 3.1 Empirische Effizienzuntersuchungen 3.2 Experimente 4 Aufgaben 5 Zum Weiterarbeiten 5.1 Extremwertsuche nach dem Verfahren des Goldenen Schnitts

Raten einer Zahl

Wir kennen das einfache Spiel zum Raten einer Zahl $z$ im Intervall $1 \le z \le max$:
Aus einem zuvor vereinbarten Intervall denkt sich ein Spieler eine Zahl, die sein Mitspieler erraten muss. Nach jedem Versuch erhält der Mitspieler den Hinweis, ob seine vermutete Zahl kleiner bzw. größer als die erdachte Zahl ist oder sogar mit ihr übereinstimmt. Die erdachte Zahl soll so mit einem Minimum an Versuchen erraten werden.
Zunächst spielen wir gegen den Computer und erraten eine Zufallszahl:

(spielerraten 100)

ausführen

Computerraten einer Zahl

Natürlich ist ein Erraten der Zahl durch sequenzielle Suche möglich. Allerdings wissen wir, dass die Suche durch Intervallhalbierung wesentlich effizienter ist.
Das Raten einer Zahl soll nun der Computer übernehmen. Dazu wollen wir selbstverständlich die effizientere Spielstrategie umsetzen:

(computerraten 47 100) --> (51 26 38 44 47)

Die Prozedur computerraten soll eine Liste mit allen "Versuchszahlen" zurückgeben. Das letzte Listenelement entspricht der zu erratenden Zahl, die Länge der Liste der Anzahl der benötigten Versuche.

(define computerraten (lambda (zahl max) ...))

(computerraten 47 100)

ausführen

Diese Strategie scheint tatsächlich schnell zum Erfolg zu führen, da in jedem weiteren Rekursionsschritt die Suche auf das halbe Suchintervall reduziert wird.
Man bezeichnet einen derartigen Suchalgorithmus als binäre Suche.
Wir testen unseren Algorithmus mit Zufallszahlen:

(define zufallszahl (lambda (max) (+ 1 (random max))))

(computerraten (zufallszahl 100000) 100000)

ausführen

Effizienz beim Raten einer Zahl

Wie viele Versuche sind mit binärer Suche im Mittel in einem vorgegebenen Intervall notwendig?
Auch hier wollen wir in grober Näherung davon ausgehen, dass jeder Versuch genau einem "Zeittakt" entspricht.

Empirische Effizienzuntersuchungen

Nun können wir wieder empirische (empirisch: aus der Erfahung oder Beobachtung) Effizienzuntersuchungen vornehmen.
Dazu definieren wir zweckmäßigerweise eine Prozedur computerraten-mehrfach, die im Gegensatz zu computerraten die Anzahl der benötigten Versuche als arithmetisches Mittel mehrerer Versuche zurückgibt.
Dabei wird jeweils eine Zufallszahl aus dem mit max begrenzten Intervall "erraten":

(define computerraten-mehrfach (lambda (max anzahl) (letrec ([summe (lambda (n) (if (= n 0) 0 (+ (length (computerraten (zufallszahl max) max)) (summe (- n 1)))))]) (/ (summe anzahl) anzahl))))

(computerraten-mehrfach 1000 10)

ausführen

Experimente

Wie bei der sequenziellen Suche automatisieren wir das Raten einer Zahl in mehreren Intervallen:

(define experiment (lambda (min max schrittweite anzahl) (if (> min max) () (append (experiment min (- max schrittweite) schrittweite anzahl) (list (computerraten-mehrfach max anzahl))))))

(experiment 500 10000 500 100)

ausführen

Die Untersuchungsergebnisse werden auch hier in einem Balkendigramm veranschaulicht:

(define rand 50) (define maxbreite (- 400 (* 2 rand))) (define maxhoehe (- 300 (* 2 rand))) (define minmax (lambda (ls) (letrec ([extremsuche (lambda (extrem ls op) (cond [(null? ls) extrem] [(op extrem (car ls)) (extremsuche (car ls) (cdr ls) op)] [else (extremsuche extrem (cdr ls) op)]))]) (cons (extremsuche 0 ls >) (extremsuche 0 ls <))))) (define balken (lambda (hoehe breite) (forward turtle breite) (left turtle 90) (forward turtle hoehe) (left turtle 90) (forward turtle breite) (left turtle 90) (forward turtle hoehe) (left turtle 90) (forward turtle breite))) (define balkendiagramm (lambda (ls) (let* ([breite (/ maxbreite (length ls))] [extremwerte (minmax ls)] [min (car extremwerte)] [max (cdr extremwerte)]) (letrec ([zeichnen (lambda (min max ls) (if (null? ls) 'ok (begin (balken (floor (* (/ (car ls) (- max min)) maxhoehe)) (floor breite)) (zeichnen min max (cdr ls)))))]) (clear canvas) (hide turtle) (move turtle rand (+ rand (* (/ max (- max min)) maxhoehe))) (right turtle 90) (zeichnen min max ls)))))

(balkendiagramm (experiment 200 10000 200 100))

ausführen

Ergebnisse:

• Die binäre Suche führt im Vergleich zur sequenziellen Suche wesentlich schneller zum Erfolg.
• Der Zeitaufwand wächst bei zunehmender Problemgröße (Suchintervall) langsamer an.
  Offensichtlich ist dieser Algorithmus bei umfassender Problemgröße sehr effizient.

Aufgaben

1. Ermitteln Sie für das Raten einer Zahl die mögliche funktionale Abhängigkeit $\mbox{Zeitaufwand} = f(\mbox{Problemgröße)}$.
   Testen Sie dazu geeignete Regressionsmodelle mit der Tabellenkalkulation oder einem grafikfähigen Taschenrechner.
2. Die Nullstellensuche in der Kurvendiskussion ist eine typische Anwendung der binären Suche.
   Verallgemeinern Sie das Raten einer Zahl und die Nullstellensuche zu einer Problemklasse, auf die eine binäre Suche anwendbar ist.

Zum Weiterarbeiten

Extremwertsuche nach dem Verfahren des Goldenen Schnitts

Die binäre Suche muss nicht zwingend zur Intervallhalbierung führen.
Ein interessanter Algorithmus ist die Extremwertsuche nach dem Verfahren des Goldenen Schnitts. Dabei überlappen sich die möglichen Suchintervalle.
Wir betrachten das Verfahren zunächst für die Suche eines lokalen Minimums:

Animation: Minimumsuche nach dem Verfahren des Goldenen Schnitts

Algorithmus (Minimumsuche): Lege ein Suchintervall durch zwei äußere Intervallgrenzen fest. Zerlege dieses Suchintervall durch einen zweimaligen Goldenen Schnitt in 3 Teilintervalle. Berechne die Funktionswerte an beiden Schnittstellen. Das neue Suchintervall wird aus der Schnittstelle mit dem größeren der beiden Funktionswerte und einer der äußeren Intervallgrenzen derart gebildet, dass die Schnittstelle mit dem kleineren Funktionswert eingeschlossen wird. Führe im neuen Suchintervall den Goldener Schnitt durch, der wieder zu 3 Teilintervallen führt. Wiederhole das Verfahren solange, bis das Suchintervall einer hinreichend kleinen ε-Umgebung genügt. Der Funktionswert eines Arguments aus dieser ε-Umgebung entspricht dem gesuchten Minimum.

Implementieren Sie den Algorithmus zur binären Suche lokaler Extremwerte (Minima und Maxima!) einer beliebigen Funktion.
Denken Sie dabei auch an das Konzept der Prozeduren höherer Ordnung!

Zur Problemlösung.