Vorlesung6

Aus ProgrammingWiki

Übungsaufgabe 1, VL S.14

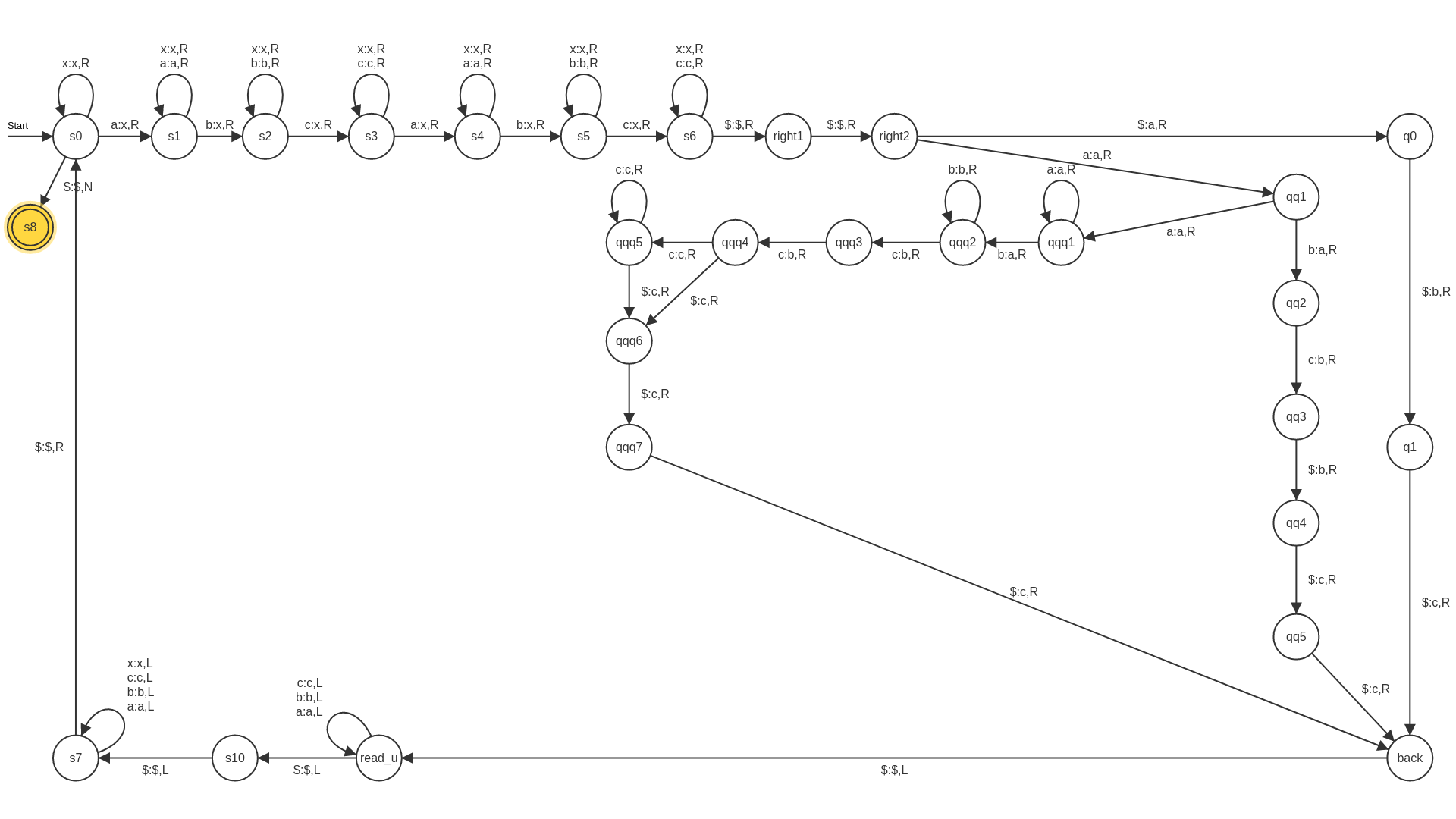
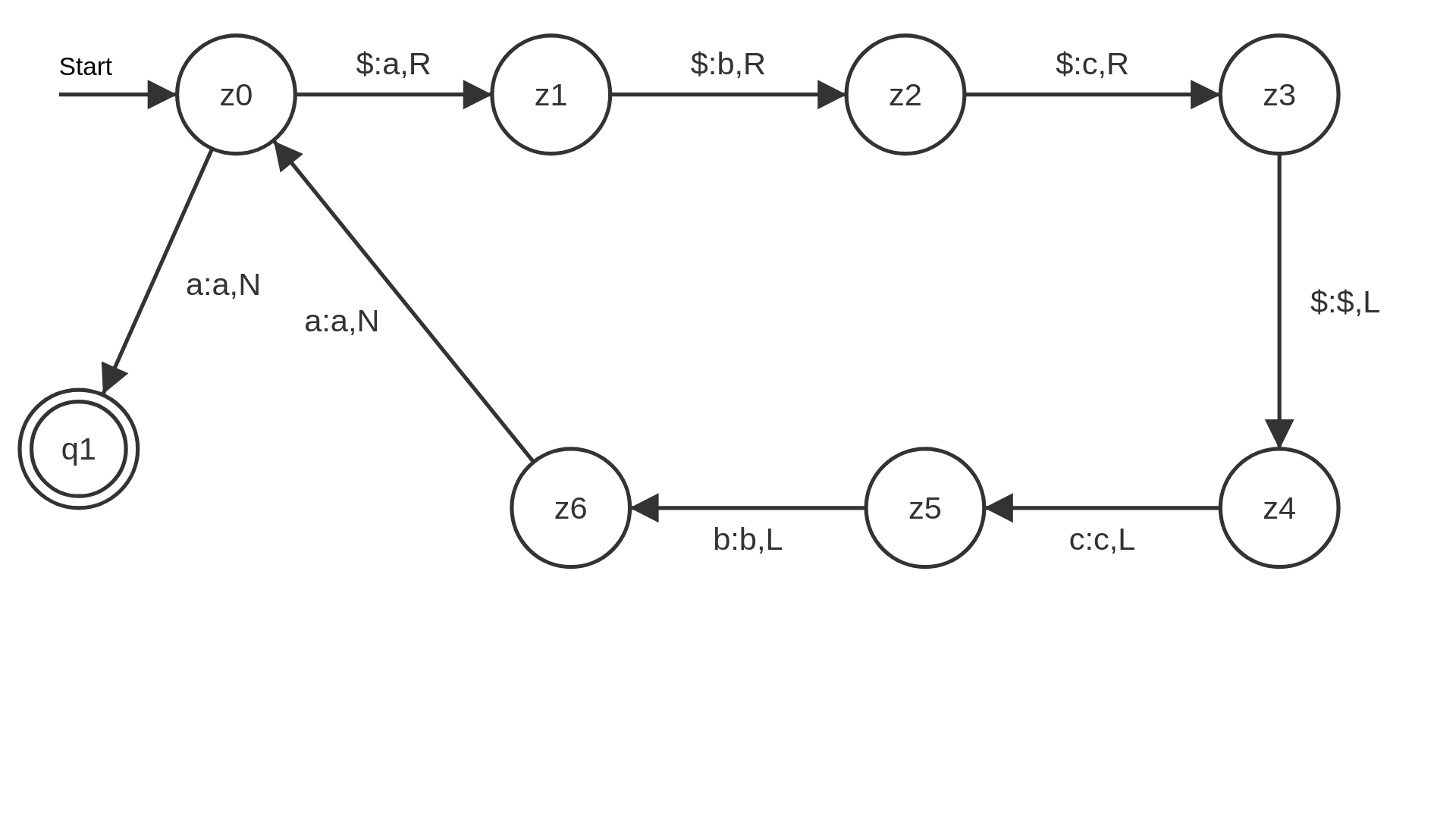
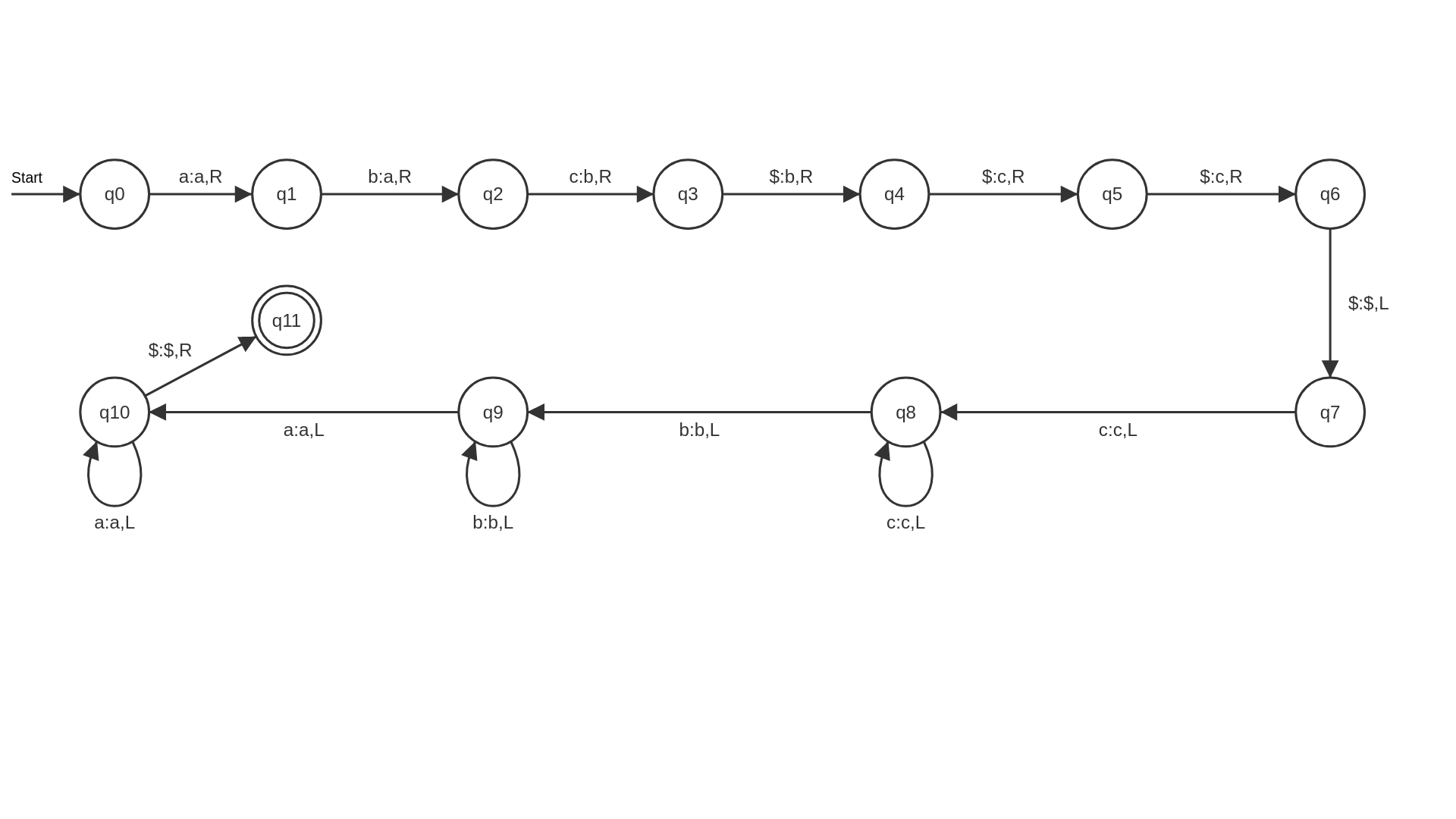
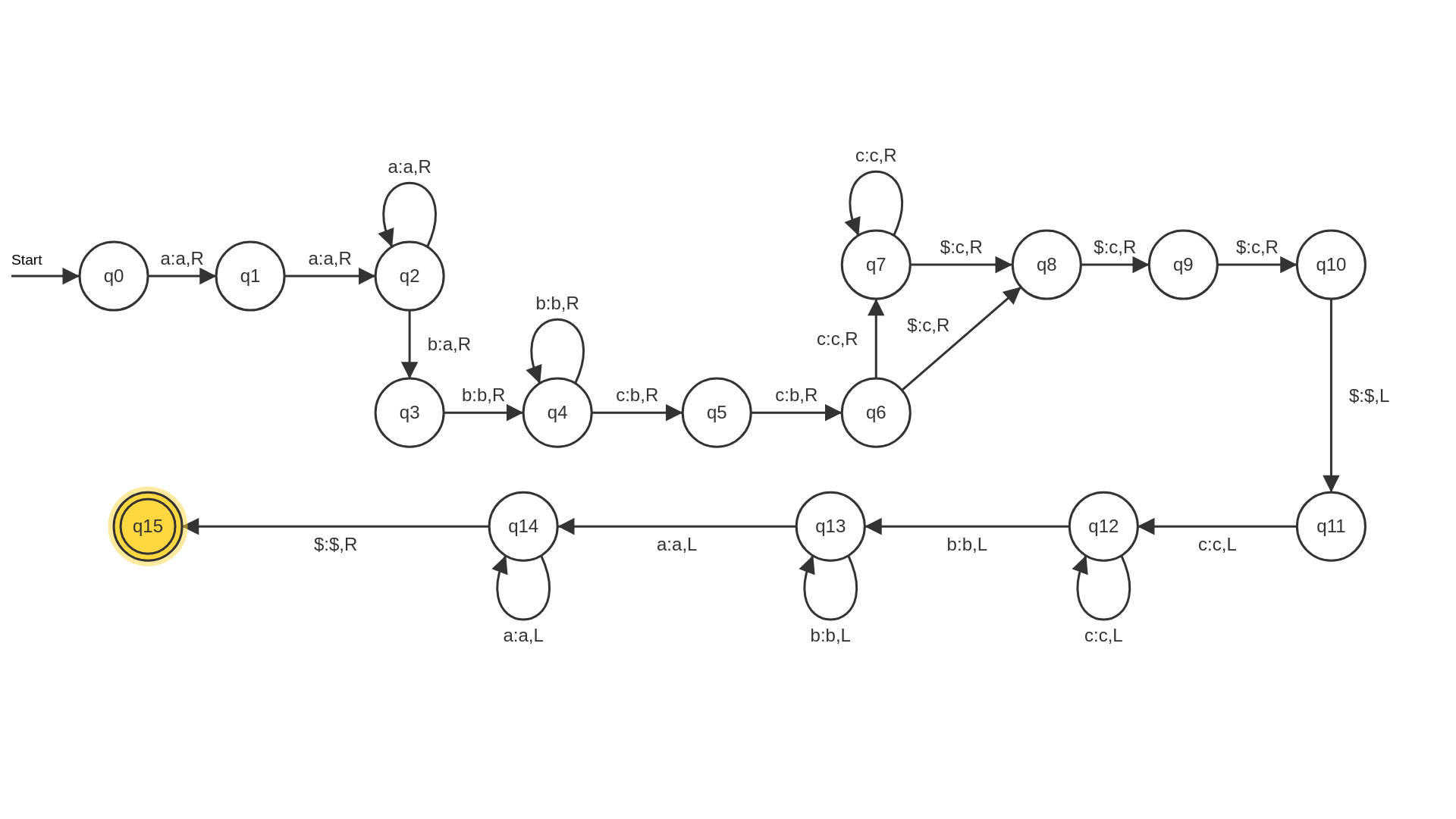
Eine TM soll überprüfen ob $w$ die Form $uu$ besitzt. Für $u$ gilt $a^ib^ic^i$, bei Korrektheit von w soll u auf dem Band hinterlassen werden.

Anmerkung: der Teil der TM, welcher das Wort $w$ auf die Form $uu$ prüft ist schon in den Vorlesungsfolien gegeben. Es geht primär darum u nach akzeptieren von $w$, auf dem Band zu hinterlassen. Hierzu kann man unterschiedlich vorgehen, im Folgenden werden die Lösungsideen vorgestellt.

   1. Die erste Idee besteht darin bei jeder iteration in der die TM $w$ auf die Form $uu$ prüft, die TM an der Stelle zu erweitern und das u entsprechend zu hinterlassen.
   2. Man könnte auch den Ansatz verfolgen wobei die TM erst $w$ akzeptiert, am Ende steht hier ein Wort auf dem Band, der Form xxxxxx auf dem Band. Hier könnte man die Hälfte des
   Wortes löschen und dann beginnen das verbleibende u von vorne und hinten zu füllen.

Erweiterung der TM:

   Die Turing-Maschine wird so erweitert, dass bei jedem Durchlauf des Wortes das vorherige Wort verdoppelt wird.
   

Vorgehen

   Um die Lösung der Turing-Maschine nachvollziehen zu können. Als erstes muss man nach dem abtasten von $w$ ein oder zwei Blankzeichen überspringen und $u$ nun erzeugen.
   Bei dem ersten Durchlauf geht man also zwei Blankzeichen weiter und erzeugt $abc$. Die Überführungsfunktion hierfür ist trivial.  
   Diese ist dargestellt in der folgenden Abbildung.
   

   Bei dem nächsten Durchlauf wird $abc$ zu $aabbcc$. Die folgende Abbildung zeigt die zugehörige TM.
   

   In allen weiteren Fällen wird jeweils genau ein b zu einem a, zwei c zu einem b und es kommen drei c hinzu. Die zugehörige TM ist unten zu sehen.
   

   Zu der endgültigen Lösung kommt man wenn man die Lösungen zusammenführt und an die jeweilige Stelle der TM aus der Vorlesung einsetzt.

Übungsaufgabe 2, VL S.17

Beweisen sie mittels Aussagenlogik $A \wedge B \rightarrow C \Leftrightarrow \neg C \wedge B \rightarrow \neg A$.

Der Beweis kann in Form einer Wahrheitstabelle erbracht werden. Dabei werden die folgenden Variabeln genutzt:

$A: P'$ ist entscheidbar

$B: P$ ist reduzierbar auf $P'$

$C: P$ ist entscheidbar

Als gegeben kann dabei nach Satz 1 betrachtet werden dass:

$A \wedge B \Rightarrow C$

zu beweisen ist:

$\neg C \wedge B \Rightarrow \neg A$

Beweis:

Folgerung: Unter Beachtung von Satz 1 und deren Richtigkeit, kann man aufgrund der Äquivalenz der Wahrheitstabelle folgende Aussage treffen. Wenn $P$ nicht entscheidbar ist und $P$ auf $P'$ reduziert wird dann ist $P'$ nicht entscheidbar.

Übungsaufgabe 3, VL S.24

Zeigen sie die Unentscheidbarkeit von $L_{\Sigma^{*}} := \{ \langle M \rangle | L(M) = \Sigma^{*} \}$ durch Reduktion des Halteproblems.

Beweisfigur:

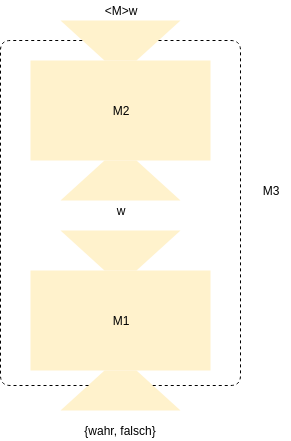
Das Halteproblem soll hierbei auf die Unentscheidbarkeit der Entscheidbarkeit der Allsprache zurückgeführt werden. Allgemein kann man zur Veranschaulichung zur Reduzierbarkeit Beweisfiguren benutzen. Dies ist oben zu sehen. $M_2$ stellt die Turing-Maschine dar, welche das Halteproblem ($L_H$) d.h. $P$ auf die Entscheidbarkeit der Allsprache ($L_{\Sigma^{*}}$) d.h. P' reduziert. $M_2$ bekommt als Eingabe eine Turing-Maschinen-Codierung und ein Wort und erzeugt ein Wort aus $\Sigma^{*}$.

Das erzeugte Wort wird der Turing-Maschine $M_1$ übergeben, diese entscheidet ob ein Wort $w$ zur Allsprache gehört oder nicht. Demzufolge ist die Ergebnismenge von $M_2 = \{ wahr, falsch \}$. $M_2$ liefert wahr, wenn das produzierte Wort $w$ in der Allsprache, der Menge aller Wörter über einem Alphabet, enthalten ist oder kurz: $w \in \Sigma^{*}$ Hierzu ist es notwendig das $\langle M \rangle w$ stoppt. $M_2$ liefert falsch, wenn das Wort $w \notin \Sigma^{*}$, d.h. $\langle M \rangle w$ stoppt nicht.

Somit kann man aus der Unentscheidbarkeit des Halteproblems, die Unentscheidbarkeit der Allsprache begründen