s3mamich
Aus ProgrammingWiki

Übungsaufgaben
Vollständige Induktion - Seite 14
Mathematische Beweismethode, nach der eine Aussage für alle natürlichen Zahlen bewiesen wird. Da es sich um unendlich viele Zahlen handelt, kann ein Beweis nicht für alle Einzelfälle durchgeführt werden. Er wird daher in zwei Etappen durchgeführt: als Induktionsanfang für eine kleinste Zahl, für die man die Aussage zeigen will, (meist 1 oder 0) und als Induktionsschritt, der aus der Aussage für eine variable Zahl die entsprechende Aussage für die nächste Zahl logisch ableitet.
Beweisverfahren:
Induktionsanfang (IA) z.z.: Es gilt $A(0)$.
Induktionsschritt (IS) z.z.: Wenn $A(i)$ gilt (Induktionsvoraussetzung, IV) , dann gilt auch $A(i+1)$ (Induktionsbehauptung, IB)
Übungsaufgabe 1.3 - Seite 15
Beweisen Sie die folgenden Beziehungen für Fibonacci-Zahlen mittels vollständiger Induktion für $ n \in \N$ und $n \geq 1$
Erste Beziehung für Fibonacci-Zahlen
$$ \sum\limits_{k=1}^{n} F_{k} = F_{n+2} - 1$$
Fibonacci-Zahlenfolge:
$F_{1}$ = 1, $F_{2}$ = 1, $F_{3}$ = 2
Induktionsanfang (IA):
z.z. Für $n = 1$ ergibt sich für die linke Seite und rechte Seite:
$F_{k}$ = $F_{n+2} - 1$
$F_{1}$ = $F_{1+2}-1$
$F_{1}$ = $F_{3}-1$
$1 = 2-1$
$1 = 1$ $\Rightarrow$ OK
Induktionsschritt (IS):
Wenn $ \sum\limits_{k=1}^{i} F_{k} = F_{i+2} - 1$ (Induktionsvoraussetzung, IV), dann gilt auch: $ \sum\limits_{k=1}^{i+1} F_{k} = F_{i+3} - 1$ (Induktionsbehauptung, IB).
$ \sum\limits_{k=1}^{i+1} F_{k} = \sum\limits_{k=1}^{i} F_{k} + F_{i+1}$ $\quad \stackrel{IV}{=}$ $ F_{i+2} -1 + F_{i+1}$ $ = F_{i+3} - 1$ (Ergebnis = IB)
Zweite Beziehung für Fibonacci-Zahlen
$$ \sum\limits_{k=1}^{n} F_{2k} = F_{2n+1} - 1$$
Fibonacci-Zahlenfolge:
$F_{1}$ = 1, $F_{2}$ = 1, $F_{3}$ = 2
Induktionsanfang (IA):
z.z. Für $n = 1$ ergibt sich für die linke Seite und rechte Seite:
$ F_{2k} = F_{2n+1} - 1$
$ F_2 = F_{2*1+1} - 1$
$ F_2 = F_{3} - 1$
$ 1 = 2 - 1 $
$ 1 = 1 \Rightarrow OK $
Induktionsschritt (IS):
Wenn $ \sum\limits_{k=1}^{i} F_{2k} = F_{2i+1} - 1$ (Induktionsvoraussetzung, IV), dann gilt auch $ \sum\limits_{k=1}^{i+1} F_{2k} = F_{2(i+1)+1} - 1 = F_{2i+3} -1$ (Induktionsbehauptung, IB).
$ \sum\limits_{k=1}^{i+1} F_{2k} = \sum\limits_{k=1}^{i} F_{2k} + F_{2(i+1)} \quad \stackrel{IV}{=} \quad F_{2i+1} - 1 + F_{2i+2} \quad = \quad F_{2i+3} - 1 $ (Ergebnis = IB)
Dritte Beziehung für Fibonacci-Zahlen
$$ \sum\limits_{k=1}^{n} F_{2k-1} = F_{2n}$$
Fibonacci-Zahlenfolge:
$F_{1}$ = 1, $F_{2}$ = 1, $F_{3}$ = 2
Induktionsanfang (IA):
z.z. Für $n = 1$ ergibt sich für die linke Seite und rechte Seite:
$ \sum\limits_{k=1}^{1} F_{2k-1} = F_{2}$
$ 1 = 1 \Rightarrow OK$
Induktionsschritt (IS):
Wenn $\sum\limits_{k=1}^{n} F_{2k-1} = F_{2n}$ (Induktionsvoraussetzung, IV), dann gilt auch $\sum\limits_{k=1}^{n+1} F_{2k-1} = F_{2(n+1)} = F_{2n+2}$ (Induktionsbehauptung, IB)
$ \sum\limits_{k=1}^{n+1} F_{2k-1} = \sum\limits_{k=1}^{i} F_{2k-1} + F_{2(i+1)-1} \quad \stackrel{IV}{=} \quad F_{2i} + F_{2(i+1)-1} \quad = \quad F_{2i} + F_{2i+2-1} \quad = \quad F_{2i} + F_{2i+1} \quad = \quad F_{2i+2}$ (Ergebnis = IB)
Übungsaufgabe 1.4 - Seite 16
Wiederholen Sie die Eigenschaften von Äquivalenzrelationen und geben Sie ein Beispiel an.
- Reflexivität: $a\sim a$
Jedes Objekt ist zu sich selbst äquivalent.
- Symmetrie: $a\sim b \ \Rightarrow\ b\sim a$
Wenn $a$ zu $b$ äquivalent ist, dann ist auch $b$ äquivalent zu $a$ (und umgekehrt).
- Transitivität: $a\sim b\ \mathrm{und}\ b\sim c\ \Rightarrow\ a\sim c$
Wenn $a$ zu $b$ äquivalent und $b$ zu $c$ äquivalent ist, dann ist $a$ äquivalent zu $c$.
Beispiel:
TODO
Übungsaufgabe 1.5 - Seite 17
Schreiben Sie ein Programm, das q berechnet.
Die im Folg. definierte Funktion $q : \R \mapsto \R$ ist an der Stelle $x=3$ undefiniert. Hierfür verwenden wir das Symbol $\bot$.
$$q(x)=\begin{cases} \dfrac{35}{x-3}, & \text{wenn }x \neq 3\text{;}\\ \bot, & \text{sonst.} \end{cases} $$
Übungsaufgabe 1.6 - Seite 17
Geben Sie sich einige Definitionsbeispiele selbstgewählter Funktionen vor. Achten Sie darauf, dass es sich auch um (echte) partielle Funktionen handeln kann. Außerdem sollten Sie einige abschnittsweise definierte Funktionen, z.B. Briefporto, Zuzahlungen für Medikamente usw., aufnehmen.
Funktion für die Berechnung des Portos von Briefen anhand des Gewichts $x$ in Gramm:
$$p(x)=\begin{cases} 0.62 , & \text{wenn }0 < x \leq 20 \text{;}\\ 0.85 , & \text{wenn }20 < x \leq 50 \text{;}\\ 1.45 , & \text{wenn }50 < x \leq 500 \text{;}\\ 2.40 , & \text{sonst.} \end{cases} $$
Übungsaufgabe 1.7 - Seite 17
Wiederholen Sie die folgenden Eigenschaften von Funktionen: injektiv, surjektiv und bijektiv. Geben Sie aussagekräftige Beispiele an. Skizzieren Sie folgende Funktionen mittels Abbildungspfeilen aus X in Y : injektiv und surjektiv; injektiv, nicht surjektiv; nicht injektiv, surjektiv; nicht injektiv, nicht surjektiv.
| Eigenschaft | Beschreibung | Beispiele |
|---|---|---|
| injektiv | Jedes Element aus Y hat höchstens einen Partner in X | $ \N \Rightarrow \N, x \rightarrow x^2 $ |
| surjektiv | Jedes Element aus Y hat mindestens einen Partner in X | $ \R \Rightarrow \R_{+}, x \rightarrow x^2 $ |
| bijektiv | Jedes Element aus Y hat genau einen Partner in X (muss injektiv und surjektiv sein) | $ \R_{+} \Rightarrow \R_{+}, x \rightarrow x^2 $ |
| Funktion $X \Rightarrow Y$ | Darstellung |
|---|---|
| injektiv,surjektiv | 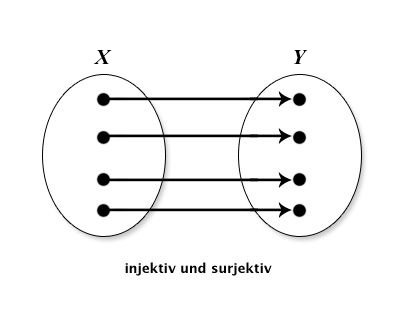
|
| injektiv,nicht surjektiv | 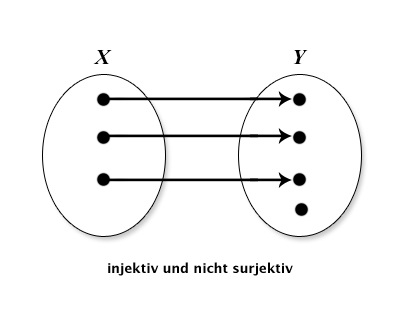
|
| nicht injektiv,surjektiv | 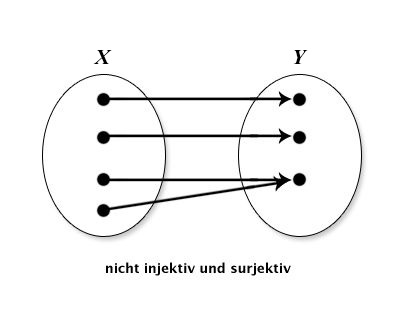
|
| nicht injektiv,nicht surjektiv | 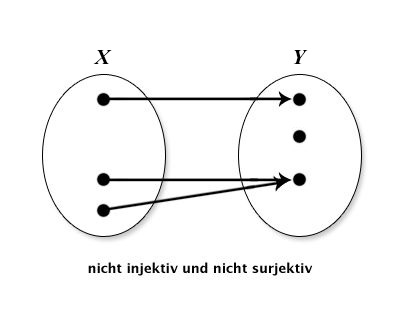
|
Übungsaufgabe Folie 22/25
Zeigen Sie, dass die Menge $\Z$ eine abzählbar unendliche Menge ist und setzen Sie sich mit der Aussage auseinander, wonach doch $\Z$ eigentlich doppelt so viele Elemente besitzt, wie $\N$.
Eine abzählbar unendliche Menge ist dadurch definiert, dass sie die selbe Mächtigkeit wie die Menge der natürlichen Zahlen hat. Man kann also jedes Element der Menge auf ein Element der natürlichen Zahlen bijektiv abbilden. Man definiert $f : \Z \to \N$:
$$f(z)=\begin{cases} −(2z+1), & \text{wenn }z < 0 \text{;}\\ 2z, & \text{wenn } z \geq 0 \end{cases} $$
Übungsaufgabe 1.8 - Seite 20
Entwerfen Sie ein Aufbauschema zur systematischen Erzeugung aller Elemente aus ℘(M) für eine gegebene endliche Menge M und wenden Sie es auf einige selbstgewählte Beispiele an.
- Leere Menge aufnehmen
- Nimm ein Element aus der Menge und füge es jedem Element der vorher gebildeten Menge Hinzu und übernimm die vorher gebildetetn Elemente
Beispiel für $ \wp(\{x,y,z\}) $
$ \wp(\{\})=\{\{\emptyset\}\} $
$ \wp(\{x\})=\{\{\emptyset\},\{x\}\} $
$ \wp(\{x,y\})=\{\{\emptyset\},\{x\},\{y\},\{x,y\}\} $
$ \wp(\{x,y,z\})=\{\{\emptyset\},\{x\},\{y\},\{z\},\{x,y\},\{x,z\},\{y,z\},\{x,y,z\}\} $
Übungsaufgaben 2te Präsentation
Turing-Maschine als Akzeptator
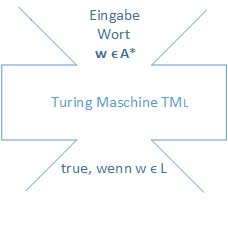
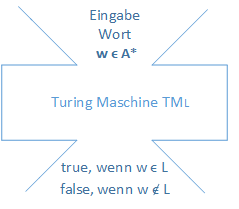
Geben Sie Trichterbilder für den Einsatz einer TM als Akzeptator an:
- für semi-entscheidbare Sprachen:
- für entscheidbare Sprachen:
Turing-Aufzählbarkeit, Turing-Entscheidbarkeit
Definieren Sie die Begriffe Turing-aufzählbar und Turing-entscheidbar analog zur Turing-Berechenbarkeit.
Sei A ein Alphabet, $M \subseteq A^*$.
- M heißt Turing-entscheidbar, wenn die charakteristische Funktion $\chi_M$
$$ \chi_M(w) = \begin{cases} wahr, & \text{wenn} w \in M;\\ falsch, & \text{wenn} w \in A^* \setminus \{M\};\\ \end{cases} $$
Turing-berechenbar ist.
- M heißt Turing-aufzählbar, wenn es eine Funktion $f: \N \rightarrow M$ gibt, die surjektiv und Turing-berechenbar ist.
Eine Funktion $f: A^* \rightarrow A^*$ heißt Turing-berechenbar, wenn es eine Turing Maschine M gibt, so dass für alle \[ w, y \in A^*\] gilt: $f (w) = y$ genau dann, wenn das Eingabewort vom Anfangszustand, nach beliebige viele Schritte stoppt in einem Endzustand mit einer Final Konfiguration.
Unentscheidbarkeitsbeweis
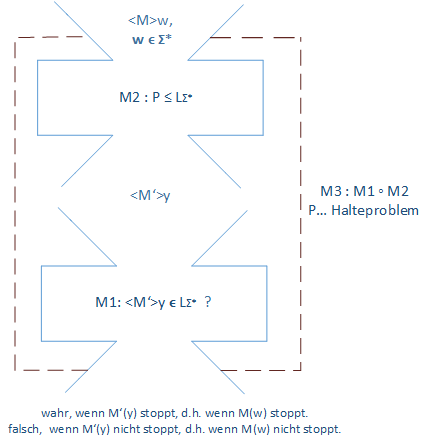
Zeigen Sie die Unentscheidbarkeit (Semi-Entscheidbarkeit) von \[ L_{\Sigma^{*}}:=\{\left\langle M \right\rangle | L(M) = \Sigma^{*} \} \] durch Reduktion der Sprache LΣ^* auf das Halteproblem.
Schreibe für alle Eingabewörter aus $\Sigma^{*}$ die Kodierung der Maschine M, also <M>, sowie w $\in$ $\Sigma^{*}$ auf das Band einer Maschine $M_2$. Die Maschine $M_2$ ist so konstruiert, dass sie aus ihrer Eingabe <M> und w die Kodierung einer Maschine M', d.h. <M'>, mit einem Eingabewort $y$ auf ihr Band als Ausgabe schreibt.
Die Besonderheit von M' ist, dass diese Maschine mit dem Eingabewort $y$ stoppt, wenn M(w) stoppen würde. Dabei ist $y$ nur ein Platzhalter, denn $y$ hat auf die Terminierung von M' keinen Einfluss. Als nächstes wird <M'> und $y$ auf das Band einer UTM $M_1$ geschrieben. $M_1$ führt die Kodierung der Maschine M' mit dem Wort $y$ aus. Dabei verwirft die Maschine M' als erstes ihr Eingabewort $y$, so dass ihr Band leer ist. Wenn die durch $M_1$ ausgeführte Maschine M' mit ihrem leeren Band hält, so heißt das, dass auch die Maschine M mit dem Wort w akzeptieren würde. Wenn die durch die Maschine $M_1$ ausgeführte Maschine M' auf dem anfangs leeren Band nicht in einem Endzustand hält, dann stoppt auch die Maschine M mit dem Wort w nicht in einem Endzustand. <M> ist $\in$ $L_{\Sigma^{*}}$ genau dann, wenn M' termiert.
Da das Halteproblem jedoch nicht lösbar ist, ist auch $L_{\Sigma^{*}}$ unentscheidbar.
Das Halteproblem ist das Problem bei einer gegebenen Programm und einer Eingaben entscheiden zu können, ob das Programm mit dieser Eingabe hält oder nicht, also entscheidet ob ein Problem hält oder nicht. In der theoretische Informatik, ob es möglich algorithmisch festzustellen, ob ein Programm bei einer Eingabe endet oder nicht, also hält. Das Halteproblem ist nicht entscheidbar.
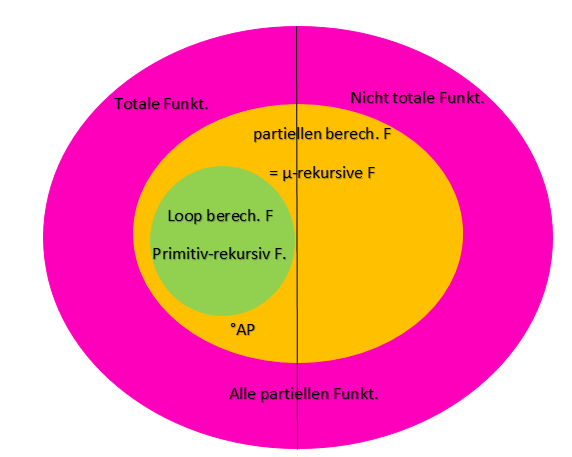
Zusammenhang der Begriffe
Funktionsklassen
- Vorlesung 9, Folie 46/46
- Vorlesung 11, Folie 22/39
- Kreativität