Aus ProgrammingWiki

Kreativaufgaben

Schnittmengen-Aufgabe

Satz:

Die Durchschnittsmenge $M_1 \cap M_2$ zweier aufzählbar unendlicher Mengen $M_1, M_2 \subseteq A^*$ ist eine aufzählbare Menge.

Beweis:

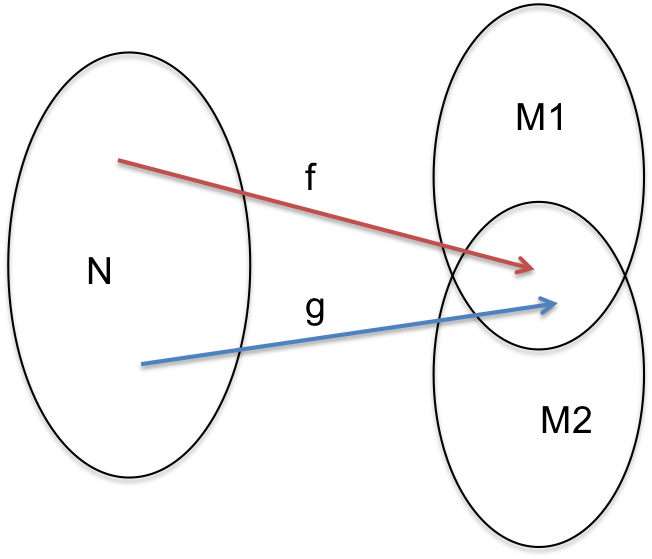
Gegeben sind die Aufzählprozeduren $f$ und $g$ für die surjektiven Funktionen $f: N \mapsto M_1$ und $g: N \mapsto M_2$.

Hierfür kann eine Aufzählfunktion definiert werden: $h: \N \mapsto M_1 \subseteq M_2$ mit

$$ h(i) = \begin{cases} f(\frac{i}{2}), & \text{wenn } i \text{ gerade };\\ g(\frac{i - 1}{2}), & \text{sonst}. \end{cases} $$

$h$ ist berechenbar, da $f$ und $g$ fur alle natürlichzahligen Argumente berechenbar sind.

Problem: Es kann nicht geprüft werden, ob ein Element aus M1 auch in M2 enthalten ist, da die Funktion nie terminieren würde bevor alle Elemente aufgezählt sind.

Idee: Falls die Schnittmenge nicht leer ist, gibt es zwei Listen, wobei nachgeschaut wird ob das jeweilige Element $f(n)$, bzw. $g(n)$ in der anderen Liste enthalten ist.

Prozedur:

;; Selektoren (define stream-car (lambda (s) (car (force s)))) (define stream-cdr (lambda (s) (cdr (force s)))) ;; Konstruktoren (define-syntax stream-cons (syntax-rules () ((_ x str) (delay (cons x str))))) (define make-stream (lambda (seed proc) (letrec ((stream-builder (lambda (n) (delay (cons n (stream-builder (proc n))))))) (stream-builder seed)))) ;; Operationen mit streams (define stream-item (lambda (str k) (if (= k 0) (stream-car str) (stream-item (stream-cdr str) (- k 1))))) (define stream->list (lambda (str n) (if (= n 0) '() (cons (stream-car str) (stream->list (stream-cdr str) (- n 1)))))) (define stream-map (lambda (f str) (delay (cons (f (stream-car str)) (stream-map f (stream-cdr str)))))) (define print-stream (lambda (str items) (if (<= items 0) (begin (display "...")(newline)) (begin (write (stream-car str)) (display ", ") (print-stream (stream-cdr str)(- items 1)))))) (define fib (lambda (n) (if (< n 2) 1 (+ (fib ( - n 1)) (fib ( - n 2))))))

(define nat-stream (make-stream 0 (lambda (i) (+ i 1)))) (define oddstream (stream-map (lambda (i) (+ 1 (* 2 i))) nat-stream)) (define evenstream (stream-map (lambda (x)(* 2 x)) nat-stream)) (define fibstream (stream-map fib nat-stream)) (define stream-intersection (lambda (m1 m2) (letrec ((intersec-f (lambda (m1 m2 list1 list2) (let ((x (stream-car m1))) (if (member x list2) (stream-cons x (intersec-g (stream-cdr m1) m2 list1 list2)) (intersec-g (stream-cdr m1) m2 (cons x list1) list2))))) (intersec-g (lambda (m1 m2 list1 list2) (let ((x (stream-car m2))) (if (member x list2) (stream-cons x (intersec-f m1 (stream-cdr m2) list1 list2)) (intersec-f m1 (stream-cdr m2) list1 (cons x list2))))))) (intersec-f m1 m2 '()'()))))

(print-stream nat-stream 10)

ausführen

(print-stream oddstream 10)

ausführen

(print-stream fibstream 10)

ausführen

(print-stream (stream-intersection nat-stream fibstream) 5)

ausführen

(print-stream (stream-intersection oddstream fibstream) 5)

ausführen