sitosalz
Aus ProgrammingWiki

Inhaltsverzeichnis |
Übung 2
Aufgabe 2
$$ \sum\limits_{k=1}^{n} F_{2k} = F_{2n+1} - 1$$
IA:
Für $n = 1$ ergibt sich:
$ F_2 = F_{2*1+1} - 1$
$ F_2 = F_{3} - 1$
$ 1 = 2 - 1 $
$ 1 = 1 \Rightarrow OK $
IS:
Wenn $ \sum\limits_{k=1}^{i} F_{2k} = F_{2i+1} - 1$ (IV), dann gilt auch:
$ \sum\limits_{k=1}^{i+1} F_{2k} = F_{2(i+1)+1} - 1 = F_{2i+3} -1$ (IB)
$ \sum\limits_{k=1}^{i+1} F_{2k} = \sum\limits_{k=1}^{i} F_{2k} + F_{2(i+1)} \quad \stackrel{IV}{=} \quad F_{2i+1} - 1 + F_{2i+2} \quad = \quad F_{2n+3} - 1 $
Übung 3
Aufgabe 5
Eine Menge $M \subseteq A^*$ ist semi-entscheidbar, wenn die partielle (semi-charakteristische) Funktion $\chi'_M : A^* \mapsto \{wahr\} $ mit $$ \chi'_M(w) = \begin{cases} wahr, & \text{wenn } w \in M;\\ \bot, & sonst. \end{cases} $$ berechenbar ist.
ÜA: Weisen Sie nach, dass die Menge M aller "Wörter aus {a, b}*, die mit a beginnen, semi-entscheidbar ist.
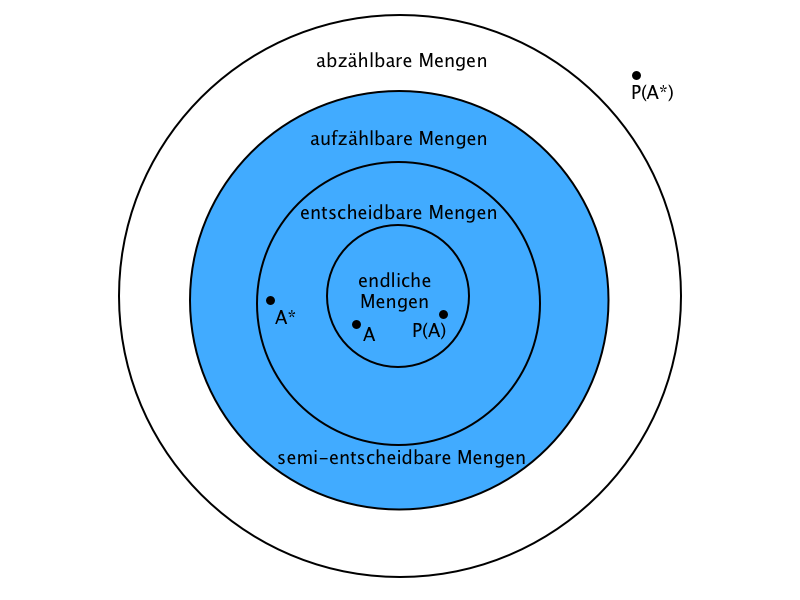
Wie in der Übersicht zu den Mengenklassen ersichtlich, ist eine Menge auch semi-entscheidbar, wenn Sie entscheidbar ist.
In Aufgabe 2 wurde die Entscheidbarkeit dieser Menge gezeigt, daraus folgt das Sie auch semi-entscheidbar sein muss.
Weiterhin kann auch eine partielle semi-charakteristische Funktion angegeben werden:
ÜA: Das Halteproblem ist semi-entscheidbar. Beweisen Sie diese Aussage.
Man kann eine Prozedur haelt? angeben, welche angewand auf eine Prozedur f true zurück gibt falls f terminiert und ansosnten ewig weiter läuft, für diesen Fall also nicht definiert ist.
Das Halteproblem ist somit semi-entscheidbar, weil eine partielle Funktion hierfür angegeben werden kann.
Übung 4
Herleitung der Funktionen für $x$ und $y$ aus $z = (x; y)$
$z =\frac{(x+y)(x+y+1)}{2} +y = t + y;$
$w = x + y;$
$x,y,z \in \N, w,t \in \R_{0}^{+}$
$t = z - y = \frac{w(w+1)}{2} = \frac{w^{2}+w}{2} $
Die Lösung von $w^{2} + w + 2t = 0$
$w=-\frac{p}{2}+\sqrt{\left(\frac{p}{2}\right)^2-q}$
$w=-\frac{1}{2}+\sqrt{\left(\frac{1}{2}\right)^2+2t}$
$w=-\frac{1}{2}+\sqrt{\left(\frac{1}{4}\right)^2+\frac{8t}{4}}$
$w=-\frac{1}{2}+\sqrt{\frac{1+8t}{4}}$
$w=-\frac{1}{2}+\frac{\sqrt{1+8t}}{2}$
für positives $w$ ist $w = \frac{\sqrt{8t+1}-1}{2}$
Außerdem gilt:
$t \leq z $, weil $z=t+y$
$z= t + w - x$
$z \leq t + w \leq t + w + 1 = \frac{w^{2}+w}{2} + w + 1 = \frac{(w+1)^{2} + (w+1)}{2}$
Unter verwendung von $z \leq \frac{(w+1)^{2} + (w+1)}{2}$ können wir $w$ nach oben abschätzen.
$w = \frac{\sqrt{8t+1}-1}{2} \leq \frac{\sqrt{8z+1}-1}{2} \leq w+1 $
Für $z$ wird $\frac{(w+1)^{2} + (w+1)}{2}$ eingesetzt:
$\frac{\sqrt{8\frac{(w+1)^{2} + (w+1)}{2}+1}-1}{2}$
$\frac{\sqrt{8\frac{w^2+3w+2}{2}+1}-1}{2}$
$\frac{\sqrt{\frac{8w^2+24w+16}{2}+1}-1}{2}$
$\frac{\sqrt{4w^2+12w+9}-1}{2}$ = $\frac{\sqrt{(2w+3)^2}-1}{2}$ = $\frac{2w+2}{2}$ = $\frac{2(w+1)}{2}$ = $w+1$
Um die beiden natürlichen Zahlen x und y aus z zu gewinnen, ist
als erstes $w = \lfloor \frac{\sqrt{8z+1}-1}{2} \rfloor $ zu berechnen. Dann ergeben sich
$t = \frac{w(w+1)}{2}$ und $y = z -t$ sowie $x = w - y$
Beispiel: Ermittelung von $x$ und $y$ aus $z=\pi(1,3) = 13$
$y=13-\frac{w(w+1)}{2}$ = $13-\frac{(x+y)(x+y+1)}{2} $ = $13-\frac{(1+3)(1+3+1)}{2} $ $= 13 -10 = 3$
$3=3$
$x=w-y = x + y - y = 1 + 3 - 3 = 1$
$1=1$