Verzweigen und beschränken SS10
Aus ProgrammingWiki

Mark Ziener (simkzien@stud.hs-zigr.de)
Mario Reichel (simareic@stud.hs-zigr.de)
Inhaltsverzeichnis |
Entwickelte Implementierungen und Folien
Rucksackproblem mit Branch and Bound: rucksack.jar
Rundreise mit Permutation: permut.jar
Rundreise mit Branch and Bound: tsp.jar
 | PresentationBranchAndBound.pdf (0.6 MB) |
Bewerten, auswählen und expandieren
Wiederholung Systematische Suche
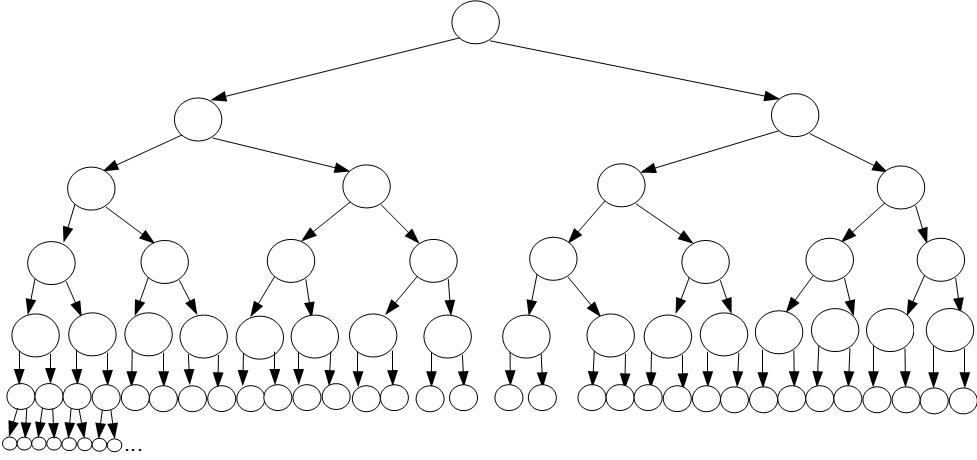
Wie bereits in vorangegangenen Vorlesungen erwähnt, können die Lösungsbäume, ob mittels Tiefe- oder Breitesuchverfahren, sehr groß werden. So kommt es bei der systematisch Vollständigen suche zu einem exponentiellen Zeitaufwand. Bei einem 0/1 Rucksackproblem mit n=6 Entscheidungen, führt dies bereits zu also 64 äußeren Knoten. In einer Baumdarstellung kann dies einen schon fast erschlagen.
Nehmen wir noch als Beispiel ein Problem mit Problemen. Dies kann man Umformen in der Form
.
Wenn man zugrunde legt das ein Rechner eine Milliarde Alternativen pro Sekunde abfragen und verarbeiten kann, so würde man für das gesamte Problem eine zeit von
Sekunden benötigen. Dies würde das geschätzte Alter der Erde von 5 Milliarden Jahre übertreffen.
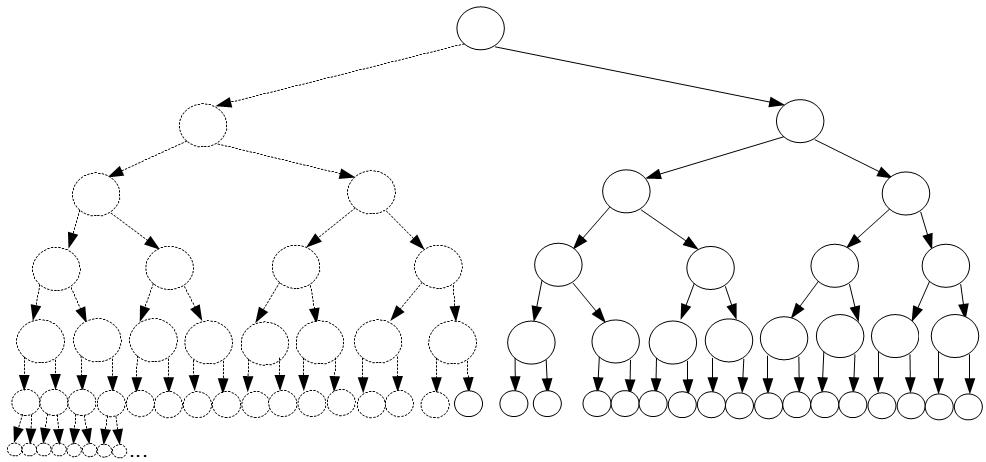
Wie kann man dem nun entgegenwirken? Man könnte versuchen bestimmte Teilbäume auszuschließen, die vermutlich zu keiner Lösung führen. Diese müssen dann nicht mehr weiter expandiert werden (was man auch als „ausästen" bezeichnet). Dieser Ansatz würde den Lösungsprozess drastisch beschleunigen, aber natürlich nichts an exponentiellen Zeitaufwand ändern sondern diesen nur verringern, im Worst-Case-Fall kann es sogar auf den selben Zeitaufwand hinaus laufen.
Diesen Denkansatz nennt man Verzweigen und Beschränken (engl. Branch and Bound). Das Hauptproblem ist das finden der nicht zu expandierenden Knoten durch einen Bewertungsalgorithmus. Je mehr Knoten dadurch aussortiert werden, desto Geringer ist der Zeitaufwand.
Das ganze wird mittels einer Wertschranke (Bound) für jeden Knoten (Branch-Schritt) bewerkstelligt. Diese Garantiert, dass keiner der Folgeknoten eine bessere Bewertung erhält als der Aktuelle.
Die Bewertung der Knoten richtet sich dabei nach der Art des Problems. Nimmt man z.B. das Rucksackproblem so handelt es sich um ein Maximierungsproblem bei dem eine obere Wertschranke gesetzt wird. Durch diese wird immer der Knoten mit der Höchsten Bewertung verfolgt.
Bei der Suche nach dem kürzesten Weg handelt es sich wiederum um ein Minimierungsproblem. Es wird eine untere Schranken angelegt und der Knoten mit der geringsten Bewertung expandiert.
Das finden einer passenden Bewertungsfunktion ist dabei das größte Problem da diese immer per Hand an das zu suchenden Ergebnis angepasst werden muss. Das finden und gegebenenfalls Editieren dieser Funktionen setzt meist eine gewisse Erfahrung voraus.
Die Komplexität des Algorithmus zur Bound Bestimmung spielt natürlich auch eine Rolle. Wenn die Wertschranke durch eine umfassende Berechnung genau bestimmt wird, fallen nahezu alle Knoten weg bis auf die zur optimalen Lösung führenden. Dadurch würde der Aufbau des Baumes zwar einen linearen Aufwand haben, der jedoch, je nach Algorithmus, mit einem enormen Berechnungsaufwand für den Bound zu kombinieren ist.
Wenn hingegen ein Algorithmus verwendet wird, dem nur eine sehr simple Berechnung zu Grunde liegt, ist kaum Aufwand nötig um die Wertschranke zu bestimmen. Doch ist diese sicherlich deutlich ungenauer wodurch man die Knoten nicht unbedingt strickt ausschließen kann, oder im Worst-Case-Fall wieder alle Knoten abarbeiten muss um die optimale Lösung zu finden. So muss man versuchen einen Mittelweg zwischen diesen beiden Extremen zu finden um einen Näherungswert für den Bound zu bilden.
Weiteres Problem ist, das durch den Näherungswert bestimmte Knoten nicht konsequent ausgeschlossen werden können. So ist es durchaus möglich, das ein Ast erweitert wird, bei dem sich später erst heraus stellt das er keine Ideale Lösung ist. Auf Grund dieser Tatsache ist es nötig, alle Knoten, sortiert nach ihrem Bound-Wert, in einer sogenannten Prioritätswarteschlange zu sammeln, um sie später evtl. wieder abrufen zu können. Später dazu mehr.
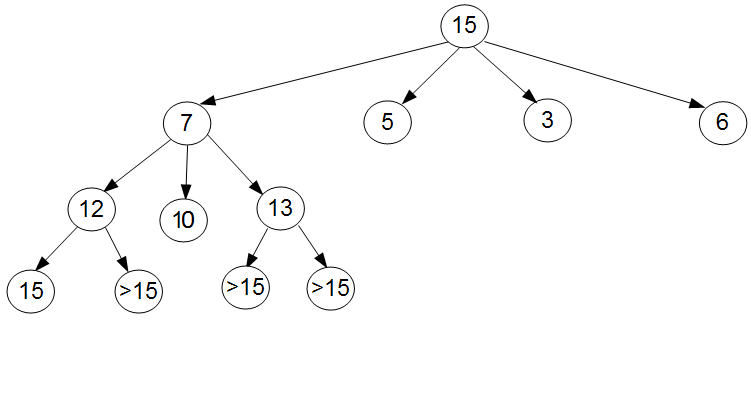
Bei der Visualisierung dieses Problems greifen wir wieder auf das Baumprinzip zurück:
Die hier verwendete Bewertungsfunktion ist eine einfache Addition der Werte, mit der Expansion beginnen wir an der Wurzel. Wir suchen nach einer Kombination aus den Werten 7 5 3 6 die 15 ergeben soll. Wir expandieren also den Knoten mit der Bewertung 7 und im Folgeschritt die 13 dieser führt allerdings nur zu Knoten deren Wert über 15 liegt und somit nicht als Ergebnis in Frage kommen. Nun ist es nötig zum Knoten mit der nächst besten Bewertung wechseln zu können welcher dann auch zum gesuchten Ergebnis 15 führt, aus diesem Grund werden alle Expansionskandidaten in einer Prioritätswarteschlange aufbewahrt. Sollten zwei Werte gleich sein, dann wird einer zufällig ausgewählt.
AVL-Baum (Prioritätswarteschlange)
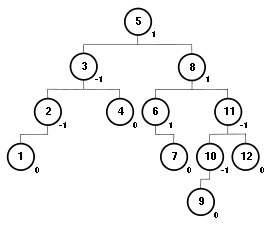
AVL-Bäume sind Datentypen, die zur Implementierung von Ranglisten oder Prioritätslisten verwendet werden können. Sie repräsentieren eine Baumstruktur, die ausbalanciert und geordnet ist.
In diesem AVL-Baum mit Balance-werten ist gut der hierarchische Aufbau zu erkennen. Ausgehend vom Wurzelelement, stehen immer links des jeweiligen Knoten kleinere Werte, rechts nur größere werte. Die Balance geht aus der Tiefe des rechten und linken Teilbaumes hervor. Wenn ein Teilbaum zu groß wird, dreht man die Elemente um eine möglichst gleichmäßiger Tiefe zu haben.
Dieser Baum muss einige Methoden beherrschen:
Einfügen eines Elementes
Der Baum wird so lang verfolgt bis ein leerer Knoten erreicht ist, in dem man den neuen Wert Speichern kann. Dabei wird im Baum Ebene für Ebene abgestiegen. Wenn der vorhandene Wert größer ist als der einzufügende, wird zum linken Ast des Elementes verwiesen. Ist der Ist der Wert kleiner, wird nach rechts verwiesen.
Suchen eines Elementes
Es wird wie bei dem einfügen eines Elementes vorgegangen. Dieser Vorgang wird Ebene für Ebene wiederholt bis entweder das zu suchende Element gefunden wurde oder der letzte Knoten erreicht ist.
Ausbalancieren eines Baumes
Durch das Ausbalancieren der Äste eines Baumes, wird wie schon erwähnt erreicht das alle Äste eine relativ gleichmäßige Länge haben. Dadurch kommt erst der große Vorteil dieser Struktur zu tragen. Wenn man in einer Langen Liste ein Element sucht müsste man die gesamte Liste durch gehen bis das Element gefunden ist. Im Worst-Case-Fall ist dies ein aufwand von . Bei einem ausbalancierten Suchbaum hingegen liegt dieser Aufwand bei
.
Die AVL-Baum ist entartet, sobald der Wert für die Balance an einem Knoten größer 1 oder kleiner -1 ist. In diesem Falle müssen Elemente in diesem Baum gedreht werden. Zur Auswahl stehen dazu die einfach rechts und links Rotation und die doppelte rechts und links Rotation.
Eine Implementierung solch eines AVL-Baumes ist in einer etwas abgewandelten Form im Beispiel "Rundreiseproblem mit Branch and Bound" zu finden.
Anwendung auf das Rucksackproblem
Anwendung auf das Rucksackproblem
Das Rucksackproblem ist ein sehr weit verbreitetes Beispiel-Problem in der Komplexitätstheorie und beschäftigt sich mit der Suche nach der effektivsten Kombination von n Gegenständen mit einem bestimmten Gewicht, sowie einem bestimmten Wert, wobei das Gewicht eine bestimmte Grenze nicht überschreiten darf.
Anwendungsbeispiele hierfür kann man sich viele denken, sei es nun das Packen des Koffers für den Urlaub oder ein Juwelendieb der vor dem Eintreffen der Polizei, mit der maximal möglichen Beute, verschwinden möchte.
Ein naiver Ansatz zur Lösung ist hier schnell gefunden, das Erzeugen aller Möglichkeiten den Rucksack zu packen und die Ausgabe der Kombination mit dem höchsten Wert. Allerdings würden sich für 60 Gegenstände Kombinationen ergeben, deren Berechnung bei vielleicht
Möglichkeiten pro Sekunde um die 30 Jahre dauern würde, bei 61 wären es dann schon über 60 Jahre. Man sieht also dass, einem ein exponentieller Anstieg, im wahrsten Sinne des Wortes schnell über den Kopf wachsen kann.
Mathematischer Formulierung:
Gegen sind:
* n = Anzahl der Objekte * gi = Gewicht von Objekt i * wi = Wert von Objekt i * G = das maximale Gewicht
Es wäre auch kein vielversprechender Ansatz die Gegenständen mit dem Höchsten Wert einzupacken, bis kein Platz mehr ist, da das Verhältnis von zu
eine Rolle spielt.
Deswegen muss ein weiterer Wert definiert werden, der die Effektivität der einzelnen Objekte beschreibt, um Sie anschließend vergleichen zu können. Diesen nennen wir
und Ordnen die Elemente nach diesem sodass sichergestellt wird das dass Element mit der besten Bewertung an erster Stelle steht, da der dazugehörige Knoten die Wurzel bildet.
Der gesuchte Ergebnisvektor ist nun
, mit
, für den gilt:
sowie
Zur Bestimmung des Bounds kann man nun auf dieser Grundlage die folgende Rechnung anwenden:
Vereinfacht kann man sagen, dass die Summe des Gewichtes aller schon im Rucksack vorhandenen Objekte addiert wird zu der Rastkapazität mal dem Quotienten das folgenden Objektes.
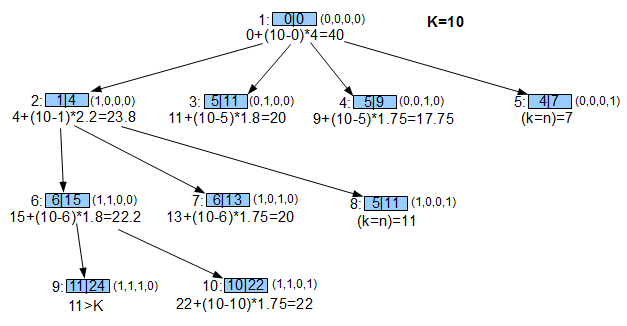
Beispiel
Wir haben 4 Objekte und eine Maximalen Kapazität von 10
Die Bewertungsfunktion ist Objektes
Geordnet ergibt sich dann
Nun bewerten wir den Wurzelknoten und es ergibt sich
Anschließend Berechnen wir für jeden Knoten den Bound und expandieren immer den Knoten mit der besten Bewertung. Dieses Objekt wird dann aus der Liste der Gegenstände entfernt, da es sich ja bereits im Rucksack befindet, so fahren wir fort bis entweder K erreicht ist oder kein Knoten mehr expandierbar ist.
Rundreiseproblem
Problemstellung
Bei dem Rundreiseproblem handelt es sich um die Problematik, der Suche, nach dem kürzesten Weg zwischen -Punkten. Dabei sollte der Ausgangspunkt immer mit dem Endpunkt übereinstimmt und jeder Punkt nur einmal besucht werden soll. Man kann das ganze also auch als Optimierungs- bzw. Minimierungsproblem sehen, in der Fachliteratur wird es auch als traveling-saleman-Problem, kurz TSP bezeichnet.
Anwendung findet diese Problematik in vielen Bereichen, natürlich ist die Logistikbranche offensichtlich aber auch Bereiche wie Maschinensteuerung sind denkbar.
Das ganze lässt sich mathematisch mit Graphen darstellen wobei die Knoten die Punkte repräsentieren und die Kanten die Verbindungen zwischen diesen.
Wir beschäftigen uns hier mit dem Symmetrischen TSP dieses zeichnet sich dadurch aus das der hin und Rückweg von Punkt zu
gleich ist, in der Realität der Autofahrer ist das natürlich nicht gegeben da sich der Hin- und Rückweg durch Einbahnstraßen usw. stark vergrößern oder verkleinern kann.
Die Entfernungen werden dabei in einer Matrix dargestellt wobei unzulässige Verbindungen mit ∞ gekennzeichnet werden.
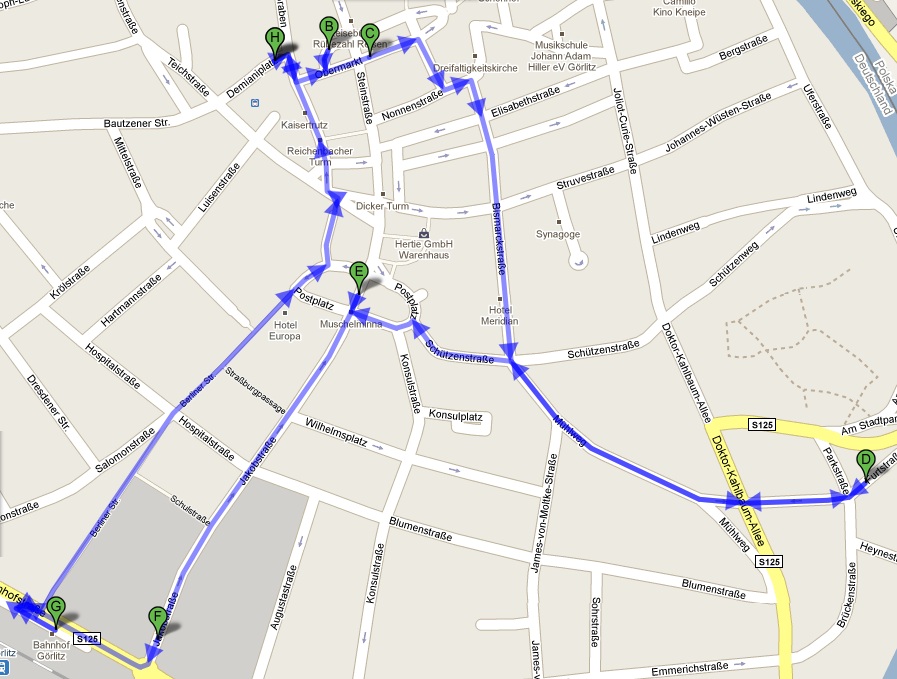
Beispiel
Ein Student muss bestimmte Dinge in der Stadt erledigen:
- Einkaufen,
- zur Post gehen,
- zur Hochschule (GIII),
- ein Buch in der Hochschulbibliothek abholen,
- etwas bei einem Mitstudenten abgeben und
- ein Bahnticket kaufen.
Dabei startet er in seiner Wohnung und hat diese auch als Ziel. Bei einem durchschnittlichen Informatikstudenten ist es dabei nahe liegend, das er darauf Wert legt, den kürzesten Weg zu wählen und möglich wenig zeit im Freien zu verbringen. Wie kann man dieses Problem mittels eines Algorithmus lösen?
| Von | Zuhause | Post | GIII | Bibliothek | Kommilitone | Bahnhof | Supermarkt |
| Zuhause | ∞ | 500 | 140 | 1500 | 1000 | 1100 | 210 |
| Post | 500 | ∞ | 400 | 1100 | 550 | 850 | 470 |
| GIII | 140 | 400 | ∞ | 1500 | 1000 | 1400 | 100 |
| Bibliothek | 1500 | 1100 | 1500 | ∞ | 1800 | 1900 | 1400 |
| Kommilitone | 1000 | 550 | 1000 | 1800 | ∞ | 400 | 900 |
| Bahnhof | 1100 | 850 | 1400 | 1900 | 400 | ∞ | 1200 |
| Supermarkt | 210 | 470 | 100 | 1400 | 900 | 1200 | ∞ |
Die Daten hierfür wurden mittels Googlemaps berechnet weswegen wie schon erwähnt der Hin und Rückweg übereinstimmen was aber in unserem Fall keinen Einfluss hat.
Naiver Algorithmus
Die einfachste Möglichkeit ist es natürlich alle möglichen Kombinationen der Punkte zu generieren, die Entfernungsmatix auf diese anzuwenden und die Ergebnisse zu vergleichen um den kürzesten Weg zu ermitteln. Den Vorgang aus Elementen
Kombinationen zu erzeugen bezeichnet man üblicherweise auch als Permutation.
Der Aufwand für den Naiven Algorithmus lässt sich recht einfach mit der Formel Berechnen und genau hier sieht man die Problematik, denn mittels der STIRLINGschen-Formel ergibt sich ein exponentieller Aufwand.
In der folgenden Tabelle kann man für ein Paar noch recht geringe Werte die möglichen Kombinationen ablesen auf die anschließend noch die Entfernungsmatix angewendet werden muss.
| Punkte | Kombinationen |
| 3 | 2 |
| 5 | 24 |
| 10 | 362880 |
| 20 | (1,216451e+17) |
| 50 | (6,082818e+62) |
| 100 | (9,332621e+155) |
Rundreiseproblem mit Branch and Bound
Wie wir bei dem naiven Algorithmus sahen, kann die Menge der verschiedenen Rundreisen sehr groß werden. So kann für eine Reise durch ein paar Städte durch den exponentiellen Aufwand schon eine unpraktikable Zeit beansprucht werden. Diese Problemstellung kann man allerdings durch das beschränken einiger Teilbäume sehr vereinfachen. Wie beim Rucksackproblem wird der Weg in einem Baum entwickelt und über Wertschranken beurteilt welcher Weg weiter verfolgt wird.
Die Frage ist nun, welche Bewertungsfunktion zur Beschränkung geeignet ist. Diese muss zum einen ja relativ einfach sein, zum anderen eine möglichst genaue Auswahl ermöglichen.
Nahe liegend wäre natürlich, einfach die Entfernung zum nächsten, noch nicht besuchten, Punkt als Bound zu verwenden. Die kann sich aber sehr schnell als Trugschluss erweisen da von diesem näheren Punkt aus evtl. nur sehr weite Wege zu den anderen noch ausstehenden Punkten führen.
Es gibt durchaus noch einige andere Algorithmen zur Bestimmung einer Näherungswertes. Einen guten Mittelwert zwischen Aufwand und Genauigkeit findet man wohl in der reduzierten Entfernungsmatrix. Dieser wird auch in einer viel Zahl von Literaturen verwendet.
Reduzierte Entfernungsmatrix
Bei der reduzierten Entfernungsmatrix geht es darum erst ein Zeilenminimum zu finden und daraus die zeilenreduzierte Entfernungsmatrix zu bilden. Aus dieser werden wiederum die Spaltenminima gebildet. Alle minimierten Werte werden anschließend Addiert um die potenziell kürzeste Strecke zu erhalten.
Abarbeitung des Algorithmus
Angelehnt an die Branch and Bound Lösung des Rucksackproblems, muss hier zuerst einmal für alle Knoten die Entfernungsmatrix editiert werden. Zuerst müssen dabei alle Werte in der Zeile der letzten Station auf unendlich gesetzt werden, ausgenommen der nächsten Station. Des Weiteren muss man alle Werte in der Zeile der nächsten Station auf unendlich setzten, wiederum ausgenommen der letzten Station. Zuletzt kann man den Wert auf unendlich setzten, der den umgekehrten Weg von der nächsten zur vorherigen Station beschreiben würde. Anschließend werden die Bound-Werte berechnet mit der beschriebenen reduzierten Entfernungsmatrix. Wenn man sich für einen Knoten entschieden hat, wird der Vorgang wiederum auf den ausgewählten Knoten angewendet. Dies wiederholt sich bis alle Stationen abgearbeitet sind. Im Falle das der Bound-Wert aller folgenden Knoten drastisch ansteigt, kann davon ausgegangen werden, das der verfolgte Pfad evtl. nicht die beste Lösung ist. Für diesen Fall müssen alle Knoten die noch nicht erweitert wurden, in einer (wie oben beschreiben) Prioritätswarteschlange gespeichert werde. So können diese Wege nach Bedarf wieder abgerufen und weiterverfolgt werden.
Für das Beispiel des Studenten lässt sich folgender Weg mit einer Strecke von 4790 m bestimmen.
Quellen
- [1] Wagenknecht, Christian
- Algorithmen und Komplexität.- Fachbuchverlag Leipzig, 2003.- ISBN 3-446-22314-2
- [2] Saake, Gunter; Sattler, Kai-Uwe
- Algorithmen und Datenstruckturen - dpunkt.lehrbuch, 2004.- ISBN 3-89864-255-0
- [3] http://de.wikipedia.org/wiki/AVL-Baum
- [4] http://de.wikipedia.org/wiki/Branch_and_bound
- [5] Google-Maps
Übung
- Gegeben sind die 4 Gegenstände, finden sie die optimale Gegenstandskombination.
Einmal mittels Breitensuche und anschließend mit Branch and Bound
K=8
Gewicht Wert 3 8 5 10 4 8 3 4 Die Bewertungsformel ist bei „Anwendung auf das Rucksackproblem-Mathematische Formulierung“ oder im Buch auf Seite. 89 zu finden
- Experimentieren sie mit dem Interaktiven Rundreiseprogramm „tsp.jar“ und überprüfen sie ob die Strecke von 4790 Metern tatsächlich die kürzeste ist.
- Reduzieren sie folgende Matrix wie im Buch beschrieben und ermitteln sie den Bound.