Systematische Suche WS13-14
Aus ProgrammingWiki

- Autoren
- Hannes Kretschmer
- Julian Hilsberg
Inhaltsverzeichnis |
Rucksackprobleme
Aus einer Menge von Gegenständen die einen Wert $w$ und ein Gewicht $g$ besitzen, gilt es einen Rucksack zu füllen bei dem der Gesamtwert der eingepackten Gegenstände maximal ist, ohne die Kapizitätsgrenze $K$ des Rucksacks zu überschreiten.
Allgemein beschreiben Rucksackprobleme: Beladungsprobleme, Verschnittprobleme oder Probleme der Budgetkontrolle.
Beispiel
Thomas will sein Geld anlegen und versucht ein Investment-Portfolio zu erstellen, aus dem er sich maximalen Gewinn erhofft. Er hat 10000€ ($K$) zur Verfügung und will diese in unterschiedliche Aktien verteilen, welche eine Bewertung ($w$) und einen festen zu investierenden Wert ($g$) besitzen. Nun geht es darum ein Portfolio zusammenzustellen (Rucksack), in welchem die Gesamtbewertung aller gekauften Aktien maximal ist, dabei darf sein Budget nicht überzogen werden.
Zur Verfügung stehende Aktien:
| Aktie | Wert (in €) | Bewertung (0-10, höher ist besser) |
| Mapple | 2500 | 8 |
| Minisoft | 3000 | 4 |
| Le-Nogo | 5000 | 5 |
| Wogitech | 6000 | 3 |
Varianten
Es gibt viele unterschiedliche Formen des Rucksackproblems:
- 0/1 Rucksackproblem:
Hier wird ein Gegenstand entweder vollständig (1) oder gar nicht (0) eingepackt. Außerdem darf der selbe Gegenstand nur einmal eingepackt werden. - Bruchteil-Rucksackproblem:
Man kann einen beliebigen Teil $t$, mit $0\% \le t \le 100\%$, eines Gegenstandes einpacken. - Unbeschränktes Rucksackproblem:
Bei dieser Variante des Problems gibt es keine Kapazitätsobergrenze, d.h. $K = \infty$. - Teilmengen-Summen-Problem (subset-sum problem):
In diesem speziellen Fall geht es darum die Gewichtskapazität des Rucksacks optimal auszunutzen, da der Wert mit dem Gewicht übereinstimmt, d.h. $g_i = w_i$ für alle $i$.
In diesem Artikel wird ausschließlich das 0/1 Rucksackproblem betrachtet. Bruchteil-Rucksackprobleme werden im Artikel der Greedy-Algorithmen behandelt.
Lösungsverfahren
Intuitives Verfahren
Ohne viel zu denken könnte man den Rucksack zufällig mit Gegenständen füllen, bis die Kapazitätsgrenze erreicht ist. Durch Austausch von jeweils 2 Objekten kann man den Gesamtwert nachträglich erhöhen. Ein im Rucksack befindlicher Gegenstand wird herausgenommen und durch einen höherwertigen, zuerst nicht eingepackten ersetzt, jedoch ohne die Kapazitätsgrenze zu überschreiten.
Dieses Verfahren ist aber nicht optimal. Erstens kann man bei diesem nicht systematischen Verfahren nie sicher sein das Wertmaximum zu erreichen.
Ein weiteres Problem tritt auf, wenn wir das obige Beispiel betrachten. Wenn man noch nachträglich die Aktien tauscht um eine bessere Bewertung des Portfolios zu erreichen, bezahlt man Gebühren für jede Transaktion und verpasst somit die Chance einer besseren Gesamtbewertung.
Tiefensuche
Das Tiefe-zuerst-Suchverfahren (engl. depth first search) oder kurz: die Tiefensuche stellt ein Lösungsverfahren für das 0/1 Rucksackproblem dar.
Ablauf
Voraussetzungen
- $w_i := g_i$
- Liste mit Gegenständen im Rucksack $s-ls$ (zunächst leer)
- Liste der Gegenstände, die in den Rucksack gepackt werden können: $g-ls$
Vorgehensweise
- mit jedem Schritt wird entschieden, ob ein Gegenstand in den Rucksack gelegt werden soll, oder nicht
- der Prozess endet (spätestens) sobald die Liste der Gegenstände außerhalb des Rucksacks leer ist
Erstellung eines Suchbaums
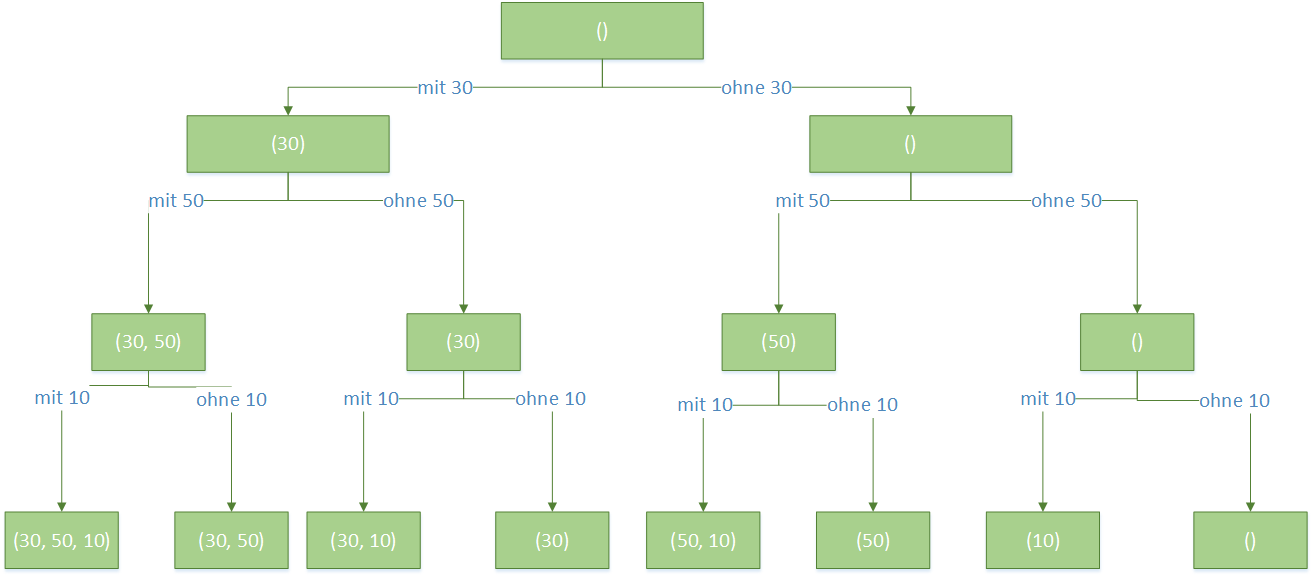
Der Entscheidungsbaum entwickelt sich dynamisch. Das heißt er wird bei der Suche von links her als ein Art Protokoll generiert. Praktisch betrachtet wird Gegenstand für Gegenstand in den Rucksack gepackt, wobei der letzte Gegenstand wieder ausgepackt, und die jeweils andere Entscheidung als zuvor getroffen wird. Hierbei spricht man von Backtracking.
Der Entscheidungsbaum im Bild rechts besitzt 8 Blätter. Es ergeben sich allgemein $2^n$ Blätter, wobei $n$ = Anzahl der Gegenstände.
Graphendurchlauf
Die Vorgehensweise bei der Tiefensuche ist identisch mit einem systematischen Baumdurchlauf (engl. tree traversal). Die Knoten werden in derselben Reihenfolge erstmalig besucht. Man spricht vom prewalk. Notiert man hingegen die Knoten erst beim zweiten, bzw. dritten Besuch spricht man vom centralwalk, bzw. postwalk.
Bewertung
Die Blätter (Blattmarkierungen) bilden die Potenzmenge der Gegenstandsmenge. Die Potenzmenge einer endlichen Menge $M$, mit $|M| = n$ besitzt $2^n$ Elemente. Für die Erzeugung des gesamten Baumes ergibt sich ein exponentieller Aufwand in .
Der Speicherplatzbedarf ist linear.
Codebeispiel
Breitensuche
Ablauf
Die Breitensuche (Breite-zuerst-Suche, engl. breadth-first search) durchläuft die Knoten eines Graphen nach der Entfernung vom Startknoten geordnet. Die direkt vom Startknoten mit einer Kante erreichbaren, werden zuerst bearbeitet, dann die mit zwei, danach die mit drei usw.
Erstellung eines Suchbaumes
Eine Alternative zur Lösung des Rucksackproblems, besteht darin den Suchbaum schichtenweise zu erstellen.
Man ist nicht gezwungen einen binären Suchbaum zu verwenden, sondern es geht darum den Suchraum durch Breitensuche eine baumartige Struktur zu geben.
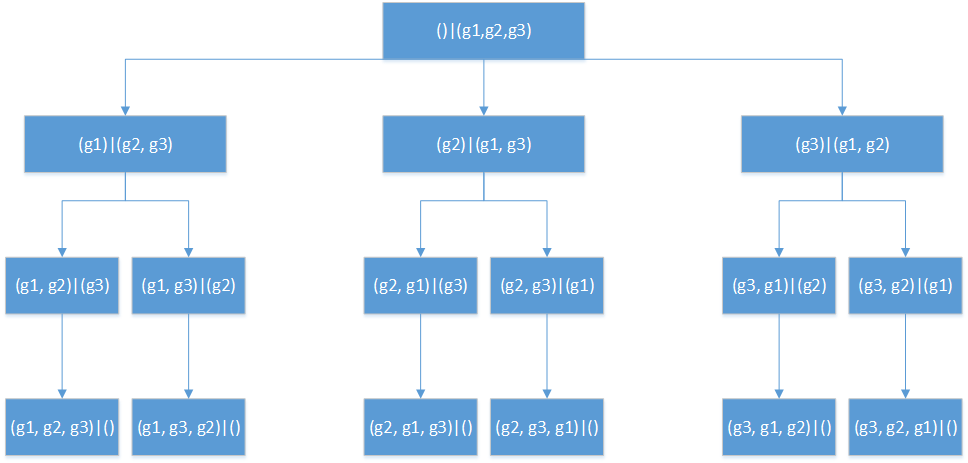
Wie auf dem rechten Bild zu sehen besitzt der Baum, für das Rucksackproblem mit drei Gegenständen genau 16 Knoten. Die Anzahl der Knoten kann berechnet werden:
Einige der Knoten sind aber überflüssig, da die Reihenfolge der eingepackten Sachen keine Rolle spielt. In dieser Form ist das Verfahren zur Lösung des Rucksackproblems ungeeignet.
Breitensuche mit verbrauchend gelesener Basismenge
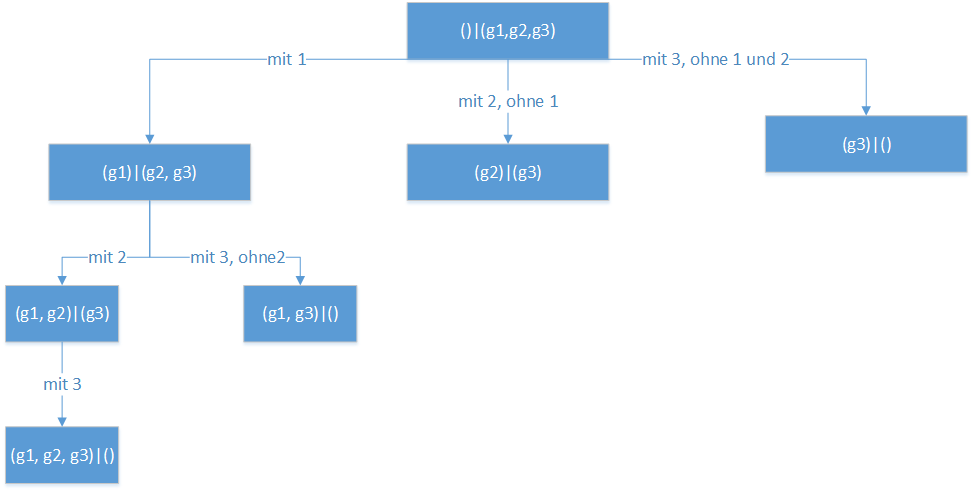
Um einen brauchbaren Suchbaum zu erhalten, muss man die Gegenstandsliste in jedem Schritt stärker minimieren, als nur durch entfernen des einzupackenden Gegenstandes.
Einen Baum auf den dieses Verfahren angewandt wurde, zeigt das Bild rechts. Schon vorgekommene Zustände werden ausgeschlossen. Die 8 Blätter zeigen sämtliche Packzustände des Rucksacks.
Laufzeit
Im Worst-Case müssen alle Knoten des Breitensuchbaumes betrachtet werden. Daher ist der Aufwand ebenfalls:
Speicherplatzverbrauch
Da alle bisher gesehenen Knoten gespeichert werden, ist der Speicherplatzverbrauch außerordentlich groß. Damit ist die Breitensuche für sehr große Probleme ungeeignet.
Beschränkung des Suchbaumes
Tiefensuche mit Beschränkung
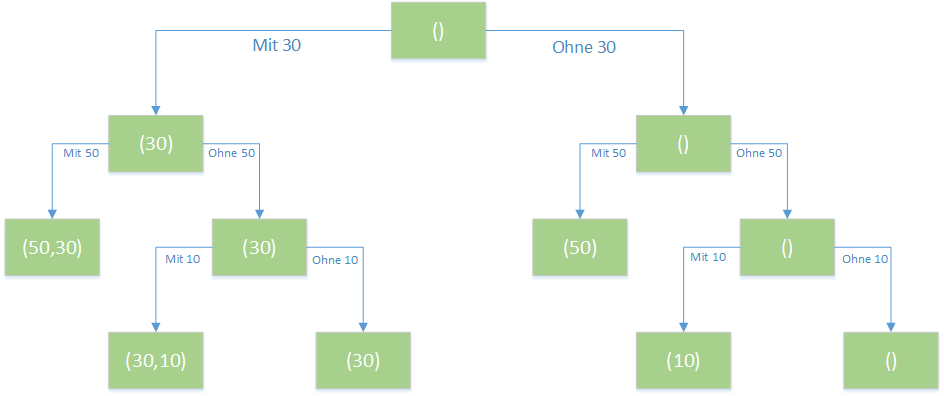
Bei der beschränkten Tiefensuche wird nun auch die Kapazitätsbeschränkung ($K$) beim "Packen des Rucksacks" mit einbezogen. Im folgenden Beispiel ist eine Prozedur zur Erstellung eines Berechnungsprotokolles zur Lösung des Problems unter Berücksichtigung von $K$ in Scheme dargestellt:
Am reduzierten Suchbaum zu erkennen ist, das lediglich die Blätter (10,30), (30), (10) und () die gewählte Kapazitätsbeschränkung erfüllen. Gesucht ist allerdings der größtmögliche Wert, d.h. bei $w_i = g_i$ wird gefordert. Da rucksack2 mit dem Aufruf (30 50 10) lediglich eine leere Liste zurückgibt, muss die Prozedur modifiziert werden. Die Prozedur rucksack3 liefert das "Blatt" des Suchbaumes mit dem größtmöglichen Wert des Rucksackinhaltes.
Nichtdeterminismus
Beim Rucksackproblem wird der Suchprozess bei der Tiefen- und Breitensuche als Baum dargestellt. Dieser Baum existiert aber nicht wirklich, d.h. er wird nicht als Datenstruktur repräsentiert.
Der Programmierer denkt in Bäumen, wenn er versucht das Verfahren in seiner Programmiersprache implementiert. Bietet die gewählte Programmiersprache das Mittel Rekursion, kann das die Arbeit weiter vereinfachen. Denn so kann die rekursive Baumstruktur direkt in eine rekursive Programmstruktur abgebildet werden. Trotzdem muss der Programmierer noch viel geistige Energie in die Organisation des Suchprozesses stecken, um einen erfolgreichen Algorithmus zu schreiben.
Um das zu realisieren eignen sich nichtdeterministische Algorithmen besonders gut.
Ein nichtdeterministischer Algorithmus "erahnt" den richtigen Pfad von der Wurzel bis zum Resultat-Blatt, falls eins existiert.
Nichtdeterminismus beschreibt eine übernatürliche Fähigkeit, das Richtige vorherzusehen.
Nun könnte man denken, durch den Einsatz des Nichtdeterminismus kann man auch die Effizienz des Algorithmus steigern, dass gelingt aber nur in den seltensten Fällen. Der Nichtdeterminismus wird durch deterministische Sprachmittel simuliert, im Hintergrund findet eine Tiefensuche statt, die bei vollständigem Durchlauf einen exponentiellen Aufwand erfordert.
Der große Vorteil vom Einsatz des Nichtdeterminismus ist die Verbesserung der kognitiven Effizienz, die hilft komplexere Probleme zu lösen.
Nichtdeterminismus in Scheme
Um den Nichtdeterminismus in Scheme zu nutzen benötigt man einige Befehle, die man zusätzlich implementieren muss.
choice: Nimmt eine Liste und gibt "das richtige Element" daraus zurück. Wenn der Befehl eingebettet ist, wird der Wert zurück gegeben, der zum "Erfolg des Gesamtausdrucks" führt.
bag-of: Nimmt eine Liste und gibt eine Liste mit den "richtigen" Elementen zurück.
multichoice: Nimmt eine Liste $ls$ und eine natürliche Zahl $n$ und gibt die $n$ "richtigen" Elemente aus $ls$ zurück.
randomchoice: Nimmt eine natürliche Zahl $n$ und berechnet das richtige Element aus der Liste (1 2 3 ... $n$).
initialize-amb-fail: Diese nullstellige Prozedur (thunk), dient zur Initialisierung des Ambiguous-Systems.
Anwendung auf das Rucksackproblem
Nun nutzen wir die nichtdeterministischen Sprachmittel um unser Rucksackproblem zu lösen.
Jetzt wird in diese Prozedur noch die Forderung nach der maximalen Gewichtssumme der eingepackten Gegenstände eingebaut.
Literatur
- Christian Wagenknecht
- Algorithmen und Komplexität - Fachbuchverlag Leipzig, 2003. - ISBN 3-446-22314-2
- Thomas H. Cormen, Charles E. Leiserson, Ronald Rivest, Clifford Stein
- Algorithmen - Eine Einführung, Oldenbourg Verlag, 2. Auflage, 2007. - ISBN 978-3-486-58262-8
- Thomas Ottmann, Peter Widmayer
- Algorithmen und Datenstrukturen, Spektrum Akademischer Verlag, 5. Auflage, 2012. - ISBN 978-3-8274-2803-5
- Markus von Rimscha
- Algorithmen kompakt und verständlich, Vieweg + Teubner Verlag, 2008. - ISBN 978-3-8348-0569-0