Greedy-Algorithmen WS13-14
Aus ProgrammingWiki
Autoren: Daniel Franke, Jens Klinger
Inhaltsverzeichnis |
Einführung
Wir haben gelernt, dass es Algorithmen gibt, die die optimale Lösung eines Problems ermitteln. Allerdings steht hier meistens ein exponentieller Aufwand dahinter.
Ist das für alle Probleme notwendig?
Greedy-Algorithmen arbeiten nach dem Motto "Nimm immer den besten Happen, den du kriegen kannst". Sie suchen den besten Weg, der an jedem Punkt vorliegt. Diese Entscheidung erfolgt auf Basis von lokalen (zu dieser Zeit vorliegenden) Informationen. Ein Zurückgehen wie bei der Tiefensuche mit Backtracking erfolgt nicht.
Auf den ersten Blick erscheint das Verfahren gut, denn der Aufwand, den man dafür benötigt, wird wohl nicht exponentiell sein.
Die Basis eines Greedy-Algorithmus ist eine bereits (absteigend) vorsortierte Liste. Wird diese erweitert, werden die entsprechenden Elemente direkt an die richtige Stelle einsortiert.
Rucksackprobleme
0/1-Rucksackproblem
Versuchen wir einen Greedy-Algorithmus auf das 0/1-Rucksackproblem anzuwenden. Dafür soll folgendes Beispiel dienen:
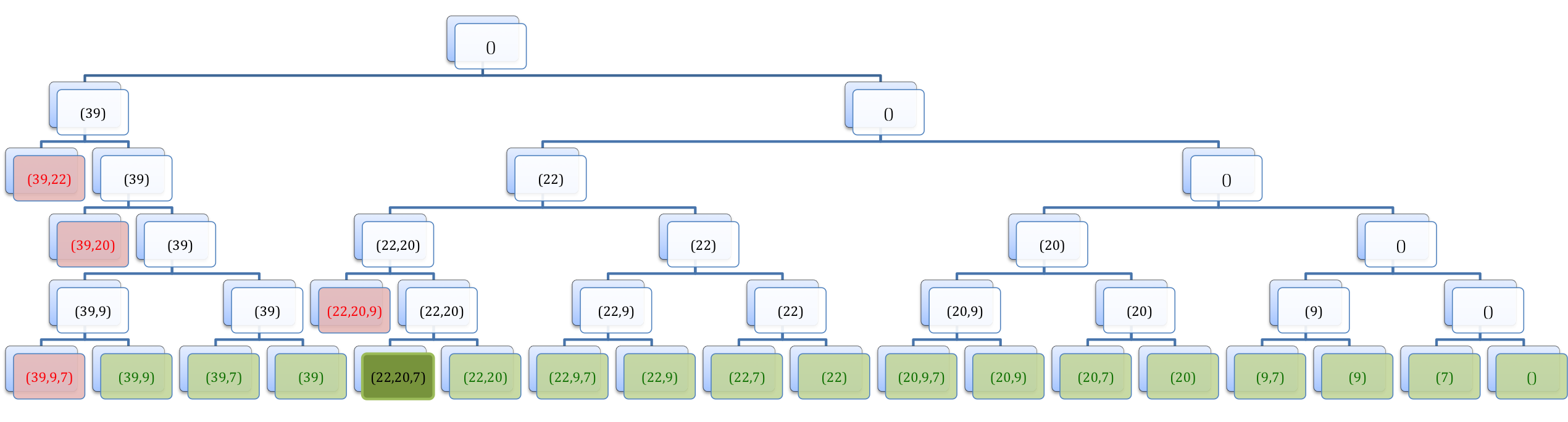
Wir haben einen Rucksack mit einem Fassungsvermögen von 50. Als mögliche Kandidaten steht die sortierte Liste (39,22,20,9,7) zur Verfügung.
Der Greedy-Algorithmus wählt nun immer das bestmögliche Teilergebnis aus. Daraus ergibt sich folgender Ablauf:
| Element | in den Rucksack | Rucksackfüllung |
|---|---|---|
| 39 | passt rein | 39 |
| 22 | passt nicht rein | 39 |
| 20 | passt nicht rein | 39 |
| 9 | passt rein | 48 |
| 7 | passt nicht rein | 48 |
Damit ergibt sich nach dem Greedy-Algorithmus eine maximale Rucksackfüllung von 48.
Betrachten wir das Problem mit einem Tiefensuchbaum, so ergibt sich jedoch eine maximale Rucksackfüllung von 49!
Bruchteilrucksack
Wie wir gesehen haben, ist ein Greedy-Algorithmus bei der Anwendung auf ein 0/1-Rucksackproblem nicht immer optimal, denn er findet nur eine Lösung.
Um diesen Missstand zu beheben, erweitern wir das 0/1-Rucksackproblem. Beim Bruchteilrucksack können auch nur Teile eines Gegenstands eingepackt werden. Dabei gehen wir davon aus, dass ein Gegenstand, der zu 70 % eingepackt wurde, auch tatsächlich einen Wert von 70 % seines Gesamtwertes besitzt. Weiterhin legen wir fest, dass das Gewicht des $i$-ten Gegenstandes einer Kandidatenliste mit $g_i$ und dessen Wert mit $w_i$ bezeichnet wird. Damit der Greedy-Algorithmus arbeiten kann, werden die $n$ Gegenstände nach ihrem spezifischen Wert, d. h. dem Quotienten aus $w_i$ und $g_i$, absteigend sortiert.
\[ \frac{w_1}{g_1} \geq \frac{w_2}{g_2} \geq \frac{w_3}{g_3} \geq \dots \geq \frac{w_n}{g_n} \]
Die Kapazität (das Maximalgewicht) des Bruchteilrucksacks sei als $K$ definiert. Es leuchtet ein, dass $K$ immer genau erreicht wird, wenn $K$ die Summe der einzelnen Gewichte $g_i$ ist. Wählt man $K$ kleiner als die Summe der einzelnen $g_i$, so kommt der Bruchteilrucksack des Greedy-Algorithmus zum Einsatz:
Es werden die ersten $j$ Gegenstände in den Rucksack gesteckt. Dabei erhalten wir $j$, indem $j+1$ das erste Element ist, das nicht mehr vollständig in den Rucksack passt. Die (eventuell noch) vorhandene Restkapazität kann nun mit einem Teil $t$ (mit $0 \leq t < 1$) des Gewichtes des $j+1$-ten Gegenstands gefüllt werden.
\[ K - \left(g_1 + g_2 + g_3 + \dots + g_j\right) = t \cdot g_{j+1} \]
Der Gesamtwert des auf diese Weise gefüllten Rucksacks beträgt nun:
\[ W = w_1 + w_2 + w_3 + \dots + w_j + t \cdot w_{j+1} \]
Aber können wir uns wirklich sicher sein, dass der Rucksack nun tatsächlich bestmöglich gefüllt ist? Man könnte ja auch auf die Idee kommen, dass man ein Element $e$ (mit $1 \leq e \leq j$) auswählt, das nun (statt komplett) nur zum Teil $y$ (mit $0 < y < 1$) eingepackt wird. Zum Auffüllen kommt dann ein weiteres (bisher vernachlässigtes) Element $r$ (mit $j < r \leq n$) mit einem geringeren spezifischen Wert zum Einsatz, das nun zu einem Teil $z$ ($0 < z \leq 1$) eingepackt wird. Dies ergibt dann den folgenden Gesamtwert
\[ W' = w_1 + w_2 + \dots + w_e + \dots + w_j + t \cdot w_{j+1} - \left( 1 - y\right) \cdot w_e + z \cdot w_r \]
Das Gewicht des $z$-ten Teil des $r$-ten Elements stimmt mit dem Restgewicht $\left( 1 - y\right) \cdot g_e$ des $e$-ten Elements überein.
\[ z \cdot g_r = \left( 1 - y\right) \cdot g_e \] \[ z = \frac{\left( 1 - y\right) \cdot g_e}{g_r} \]
Setzen wir nun dieses $z$ in die Gleichung für den Gesamtwert $W'$ ein, erhalten wir:
\[ W' = w_1 + w_2 + \dots + w_e + \dots + w_j + t \cdot w_{j+1} - \left( 1 - y\right) \cdot w_e + \frac{\left( 1 - y\right) \cdot g_e \cdot w_r}{g_r} \]
\[ W' = W - \frac{\left( 1 - y\right) \cdot g_e \cdot w_e}{g_e} + \frac{\left( 1 - y\right) \cdot g_e \cdot w_r}{g_r} \]
Wie oben festgelegt wurde, gilt $\left( 1 - y\right) \cdot g_e > 0$ und damit ergibt sich:
\[ W' = W + \underbrace{\left( 1 - y\right) \cdot g_e}_{> 0} \cdot \underbrace{\left( \frac{w_r}{g_r} - \frac{w_e}{g_e}\right)}_{< 0} \]
Hier wird deutlich, dass kein Wertzuwachs erfolgt, sondern stattdessen sogar $W' < W$ gilt. Dies zeigt also, dass der Greedy-Algorithmus das Bruchteilrucksack-Problem effizient löst.
Aufbau eines Greedy-Algorithmus
Ein Greedy-Algorithmus kann im Allgemeinen durch folgende Bestandteile beschrieben werden:
- Listen
- Kandidatenliste
- Resultatsliste
- Funktionen
- loesung? prüft, ob die ermittelte Resultatliste eine mögliche Lösung des Problems darstellt
- okay? prüft, ob aktueller Kandidat in Resultatliste aufgenommen werden kann
- naechster wählt nächsten Kandidaten aus
- modify+ erweitert die Kandidatenliste
- modify- streicht einen nicht verwendbaren Kandidaten aus der Kandidatenliste
- ziel gibt die Resultatliste aus
Allgemeine Form
Diese Bestandteile können wir mit Scheme bzw. Racket in Form einer Prozedur angeben, die allgemein gültig ist:
Diese hier geschriebene Prozedur (Quelle: [1], S. 115) kann man als Template für alle Greedy-Algorithmen übernehmen. Nur im oberen Bereich müssen die Punkte (...) durch entsprechende Funktionen angepasst werden.
Beispiel
Eine genaue Funktionsweise der oben dargestellten Prozedur wird anhand eines Geldwechsel-Beispiels verdeutlicht.
Problemstellung: Ein beliebiger Wechselgeldbetrag in Euro soll mit so wenig wie möglichen Münzen zurück gegeben werden. Damit können wir unsere Kandidatenliste in Form von Cent-Beträgen absteigend sortieren:
(200 100 50 20 10 5 2 1)
Die Funktion loesung? liefert #t, wenn die Summe der ausgewählten Münzen genau den gesuchten Betrag ergibt.
In der Funktion okay? wird geprüft, ob die Summe der gewählten Münzen höchstens dem gesuchten Betrag entspricht. Sobald das nicht mehr der Fall ist, wird mithilfe der Funktion modify- der gegenwärtige Kandidat aus der Liste der potentiellen Kandidaten gestrichen. Da wir hier von einer idealen Kasse ausgehen, die unendlich viele Münzen beinhaltet, lässt die Funktion modify+ die Liste der Kandidaten in diesem Fall unverändert.
Die Funktion naechster gibt immer den ersten Wert aus der Kandidatenliste zurück - ganz gleich, ob damit der Gesamtwert überschritten wird, oder nicht. Die Summe wird dann von okay? geprüft. Aufgrund der absteigend vorsortierten Liste können wir immer davon ausgehen, dass der höchstmögliche Kandidat geprüft wird.
Die verbleibende Funktion ziel gibt bei einem erfolgreichen Wechselvorgang die Liste der Einzelmünzen und die Anzahl der gefundenen Münzen aus.
Verschiedene Algorithmen
Exkurs: Allgemeines zur Graphentheorie
Das folgende Problem ist der Betrachtung von Graphen zuzuordnen. Graphen sind eine mathematische Struktur, die aus Knoten und Kanten bestehen. Eine Kante verbindet dabei genau zwei Knoten. Knoten können mit mehreren anderen Knoten verbunden werden. Es ist aber nicht erforderlich, dass alle Knoten miteinander verbunden sind.
Eigenschaften von Graphen:
- gerichtet - Die Richtung, in die die Kante gilt, ist durch einen Pfeil angegeben.
- ungerichtet - Die Kante gilt in beide Richtungen.
- gewichtet - Der Kante ist ein Wert (z. B. eine Entfernung) zugeordnet.
- ungewichtet - Die Kante hat keinen Wert.
- zusammenhängend - Alle Knoten sind miteinander verbunden.
Zur Speicherung von Graphen werden oft Matrices - insbesondere Adjazenzmatrices - verwendet. Ist es ein gewichteter Graph, so werden zu jedem Knotenpaar die Werte der Kanten angegeben. Existiert eine Kante nicht, so wird dies meist mit $0$ oder $\infty$ beschrieben.
Dijkstra-Algorithmus
Kürzeste Wege in Graphen
Das Rundreiseproblem haben wir bereits behandelt. Die bisher hierfür bekannten Lösungsmöglichkeiten bieten nur einen exponentiellen Aufwand.
Bei dem hier betrachteten Problem gehen wir noch ein Stück weiter: Bei der Reise von Stadt $A$ nach Stadt $B$ ist für jede der unterwegs besuchten $n$ Städte wiederum eine Entfernungsmatrix gegeben, die die Entfernung zu allen umliegenden Städten beinhaltet. Dies scheint auf den ersten Blick noch mehr Aufwand zu bedeuten.
Der Algorithmus des Informatikers Edsger Dijkstra benötigt einen Aufwand, der in $\mathcal{O}\left( n^2\right)$ liegt. Die Informatiker Robert Floyd und Stephen Warshall erweiterten diesen Algorithmus noch weiter, so dass hier die kürzesten Entfernungen zwischen allen Städten ermittelt werden. Dieser Algorithmus hingegen arbeitet dann in $\mathcal{O}\left( n^3\right)$.
Der Algorithmus lässt sich mit folgendem Pseudocode beschreiben:
/*
* S: Lösungsmenge
* s: Startknoten
* V: Menge aller Knoten des Graphen
* z: Zielknoten
*/
S := {s};
Distanz(s) := 0;
for all $v \in V\backslash \lbrace s\rbrace$ do {
Distanz(v) := Kante(s, v);
Vorgänger(v) := s;
}
while $z \not\in S$ do {
Finde $u \in V\backslash S$ mit Distanz(u) = min{Distanz(v) | $v \in V\backslash S$};
S := $S \cup \lbrace u\rbrace$;
for all $v \in V\backslash S$ do {
if Distanz(u) + Kante(u, v) < Distanz(v)
then {
Distanz(v) := Distanz(u) + Kante(u, v);
Vorgänger(v) := u;
}
}
}
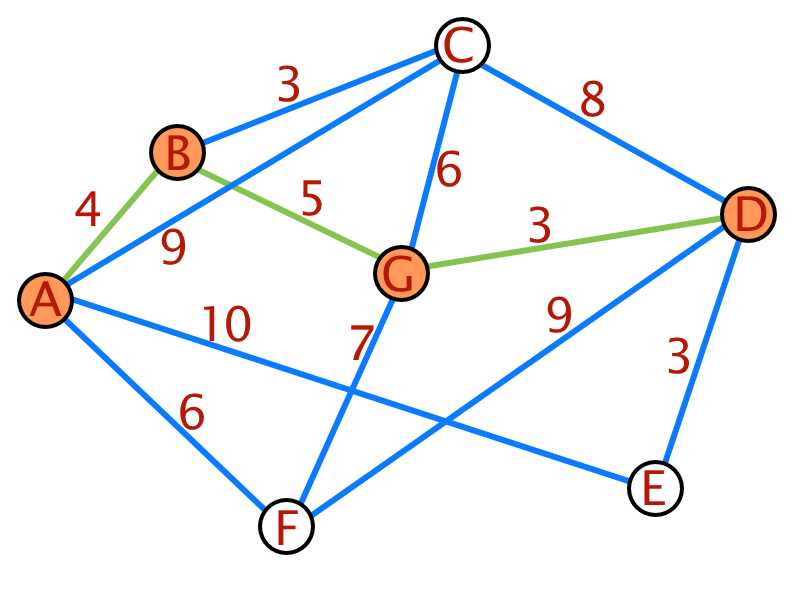
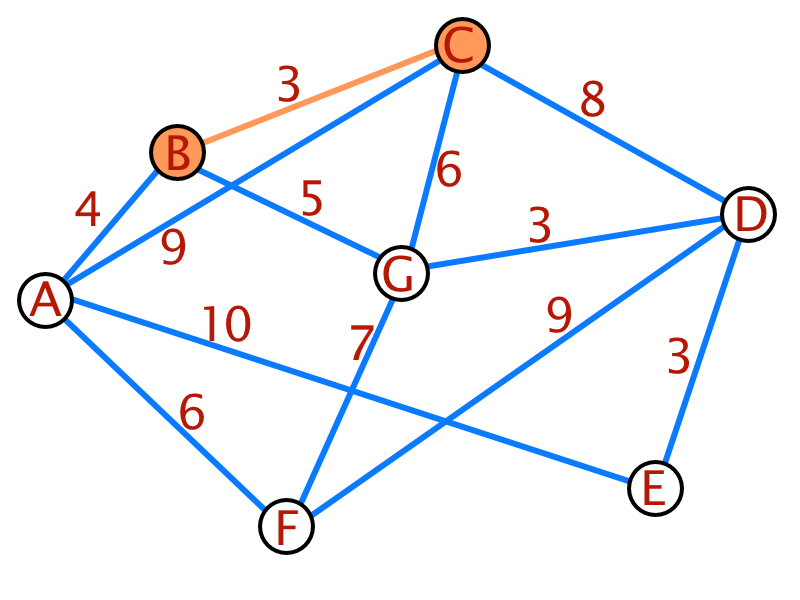
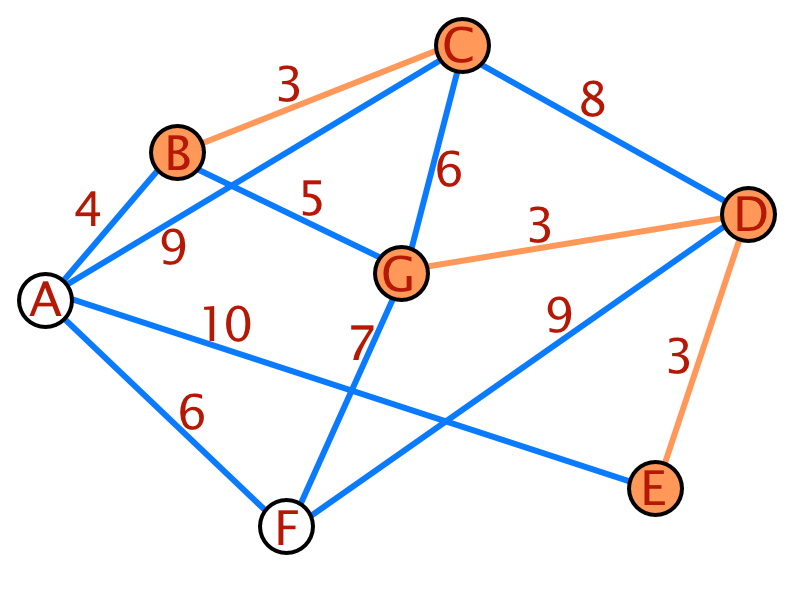
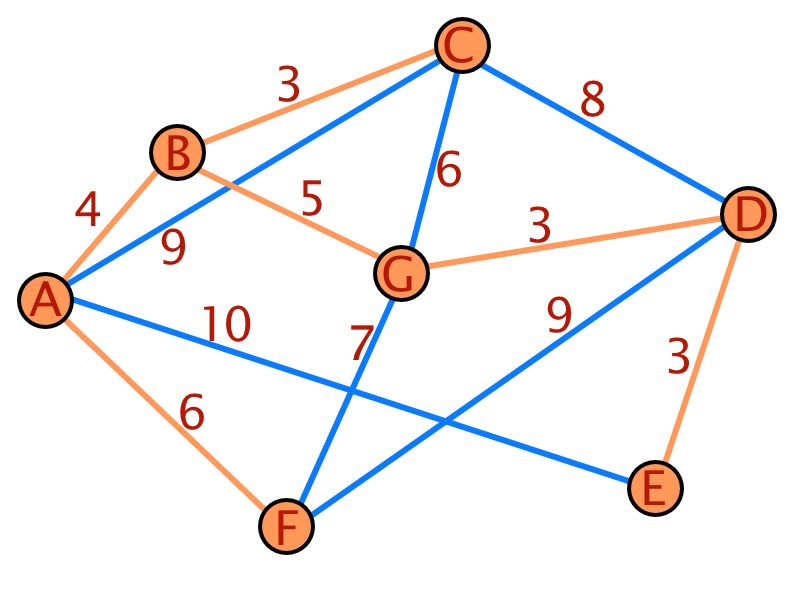
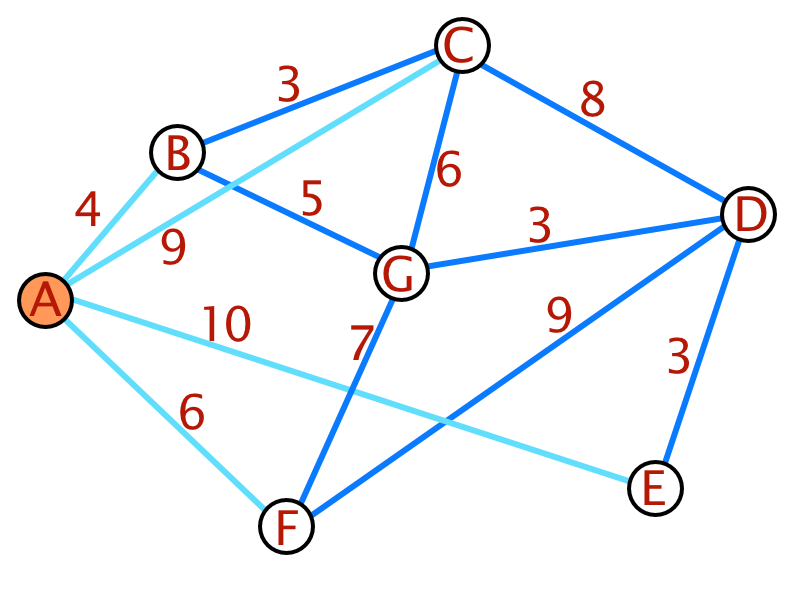
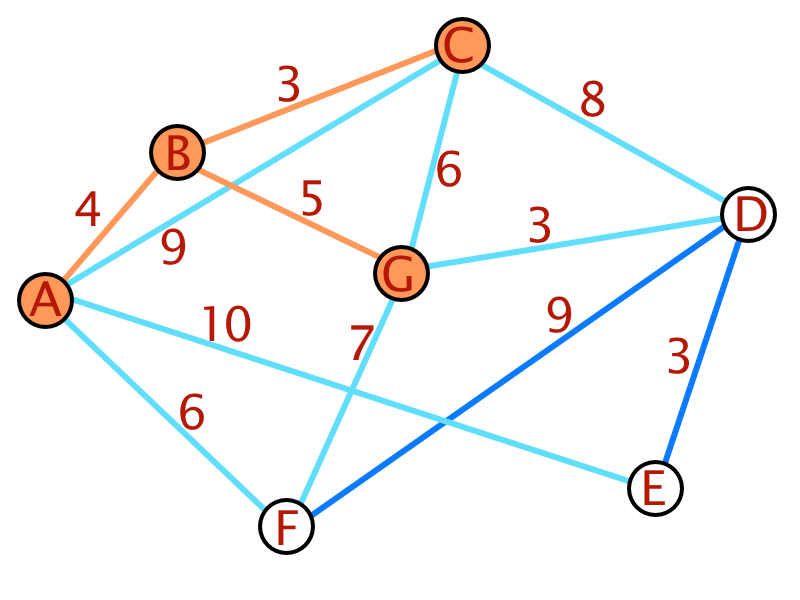
Zur besseren Verständlichkeit des Dijkstra-Algorithmus folgt ein Beispiel:
 |
|
| Schritt | A | B | C | D | E | F | G |
|---|---|---|---|---|---|---|---|
| 1 | 0 | $\infty$ | $\infty$ | $\infty$ | $\infty$ | $\infty$ | $\infty$ |
| 2 | 0 | 4 | 9 | $\infty$ | 10 | 6 | $\infty$ |
| 2 | 0 | 4 | 7 | $\infty$ | 10 | 6 | 9 |
| 3 | 0 | 4 | 7 | 15 | 10 | 6 | 9 |
| 4 | 0 | 4 | 7 | 15 | 10 | 6 | 9 |
| 5 | 0 | 4 | 7 | 12 | 10 | 6 | 9 |
 Nach dem Anwenden des Algorithmus ergibt sich dieses Bild. Die Wege zu C und F sind überflüssig. |
 Dies ist der optimierte Weg von A nach D. |
Bei sorgfältiger Implementierung kann der Aufwand für den Dijkstra-Algorithmus durchaus in $\mathcal{O}\left( \left( m+n\right) \log n\right)$ liegen, wobei $n$ die Zahl der Knoten und $m$ die Zahl der Kanten darstellen.
Minimaler Spannbaum
Die Graphentheorie nennt ungerichtete, zusammenhängende und zyklenfreie Graphen mit mindestens einem Knoten einen Baum. Verbindet ein Teilgraph eines Graphen alle Knoten miteinander als Baum, so spricht man von einem Spannbaum.
Kruskal-Algorithmus
Der Mathematiker Joseph Kruskal entwickelte einen Algorithmus zur Suche nach einem minimalen Spannbaum. Durch seine Effizienz arbeitet der Algorithmus in $\mathcal{O}\left( m \log n\right)$, wobei $m$ die Anzahl der Kanten und $n$ die Anzahl der Knoten darstellen. Sollte $m \leq n$ gelten, so arbeitet der Algorithmus in $\mathcal{O}\left( n \log n\right)$, für sehr wenige $m$, d. h. $m \leq \frac{n}{2}\left( n-1\right)$, in $\mathcal{O}\left( n^2 \log n\right)$.
Der Algorithmus lässt sich wie folgt beschreiben:
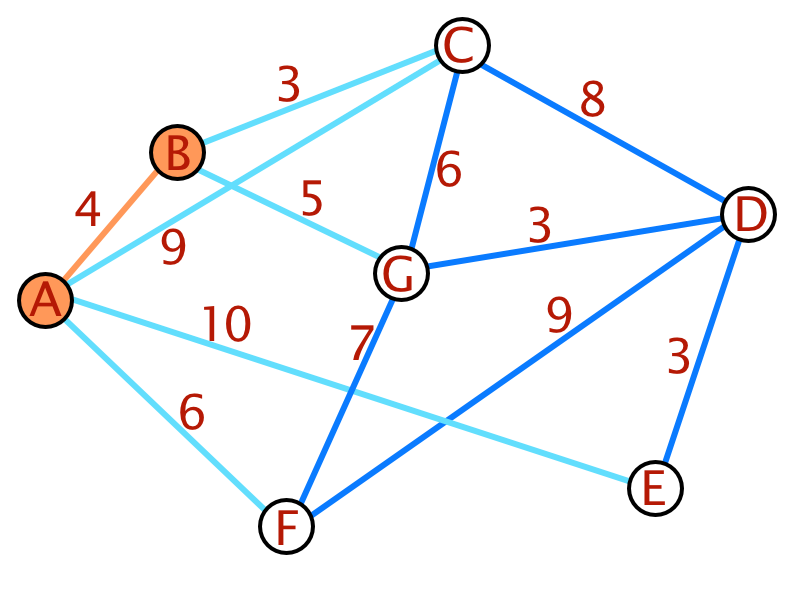
- Alle Kanten werden in aufsteigender Länge in einer Liste sortiert.
- Die erste Kante bildet mit ihren anschließenden Knoten den Startgraphen. Existeren mehrere Kanten gleicher Länge, werden alle verwendet.
- Solange noch nicht alle Knoten verbunden sind, wird dieses Verfahren wiederholt.
- Würde durch die Hinzunahme einer Kante ein Kreis entstehen, wird diese Kante aus der Liste gestrichen und mit der nächsten fortgefahren.
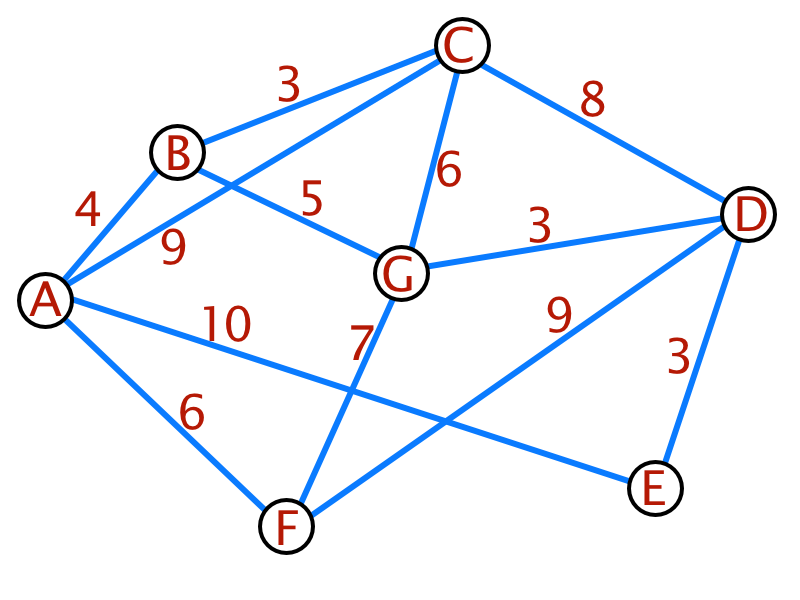
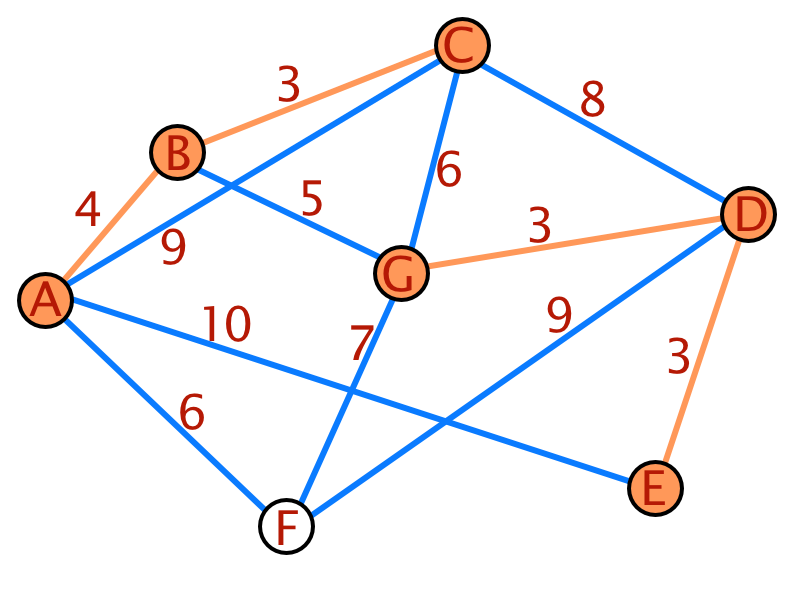
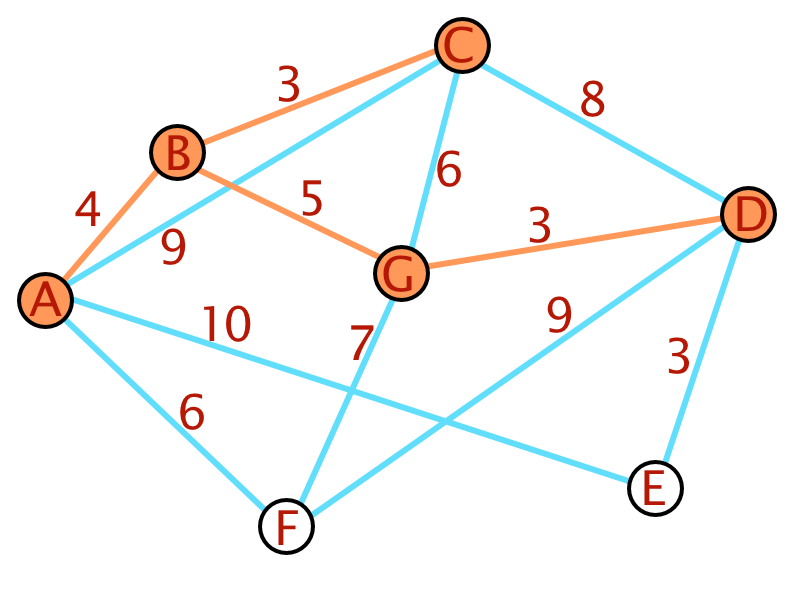
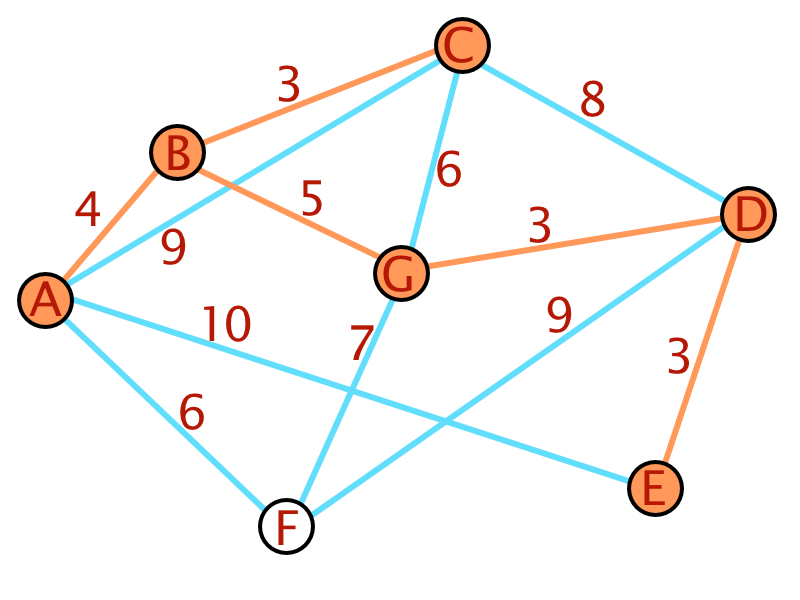
Am Beispiel wird der Algorithmus deutlich. Als Basis dient wieder der bereits weiter oben verwendete Graph.
Wir suchen uns die Kanten mit den geringsten Werten. Dies wären $\overline{BC}$, $\overline{DE}$ und $\overline{DG}$. Welche wir wählen, ist egal. |
 Wir wählen die Kante $\overline{BC}$ mit ihren zugehörigen Knoten als Startgraph. |
 Die beiden anderen Favoriten kommen ebenfalls hinzu. |
 Die nun kürzeste Strecke ist die Strecke $\overline{AB}$, die nun an den Graphen "angeschlossen" wird. |
 Mit der Strecke $\overline{BG}$ sind nun fast alle Knoten verbunden. |
 Als letzte noch fehlende Strecke kommt die Strecke $\overline{AF}$ hinzu und vervollständigt den minimalen Spannbaum. |
Prim-Algorithmus
Ein weiterer Algorithmus zur Ermittlung des minimalen Spannbaums wurde 1930 vom Mathematiker Vojtěch Jarník entwickelt, 1957 von Robert Prim und 1959 von Edsger Dijkstra wiederentdeckt. Auf Basis des Dijkstra-Algorithmus arbeitet dieser Algorithmus in $\mathcal{O}\left( n^2\right)$.
Die Funktionsweise des Algorithmus lässt sich wie folgt beschreiben:
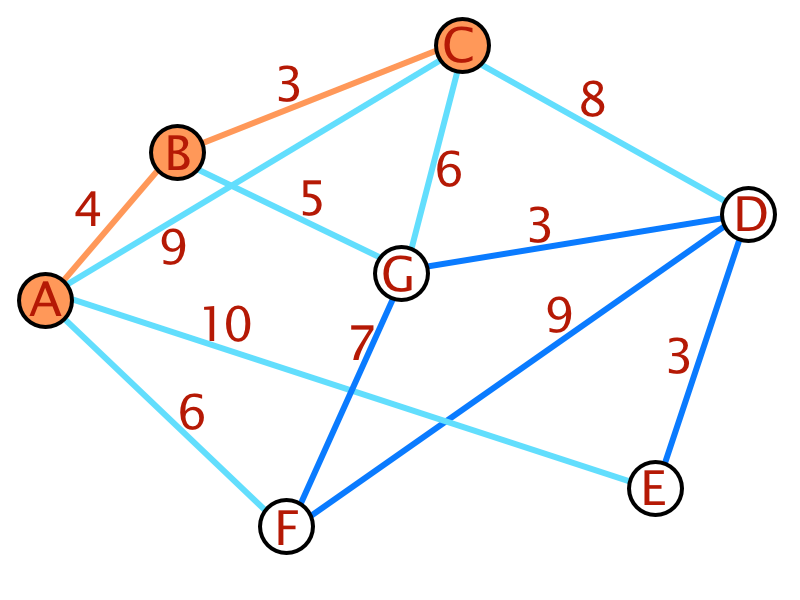
- Ein beliebiger Knoten eines Graphen wird gewählt.
- Nun wird die angrenzende Kante mit dem geringsten Wert gewählt und der angrenzende Knoten verbunden.
- Dieses Verfahren wird so lange wiederholt, bis alle Knoten verbunden sind. Es werden nun aber alle Kanten an allen verbundenen Knoten betrachtet.
- Würde durch die Hinzunahme einer Kante ein Kreis entstehen, wird diese Kante aus der Liste gestrichen und mit der nächsten fortgefahren.
Die Erweiterung der Dijkstra-Algorithmus ergibt sich dann wie folgt:
/*
* S: Lösungsmenge
* s: Startknoten
* V: Menge aller Knoten des Graphen
*/
S := {s};
Distanz(s) := 0;
for all $v \in V\backslash \lbrace s\rbrace$ do {
Distanz(v) := Kante(s, v);
Vorgänger(v) := s;
}
while $S \neq V$ do {
Finde $u \in V\backslash S$ mit Distanz(u) = min{Distanz(v) | $v \in V\backslash S$};
S := $S \cup \lbrace u\rbrace$;
for all $v \in V\backslash S$ do {
if Kante(u, v) < Distanz(v)
then {
Distanz(v) := Kante(u, v);
Vorgänger(v) := u;
}
}
}
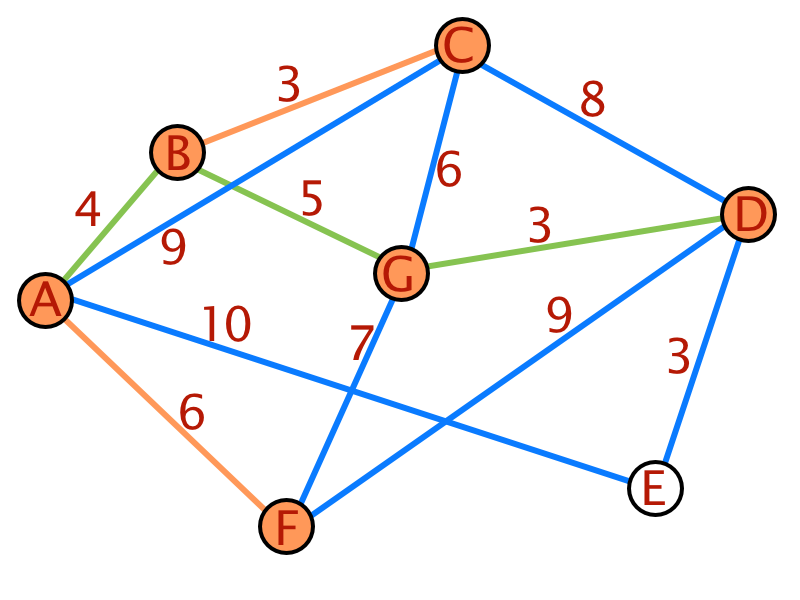
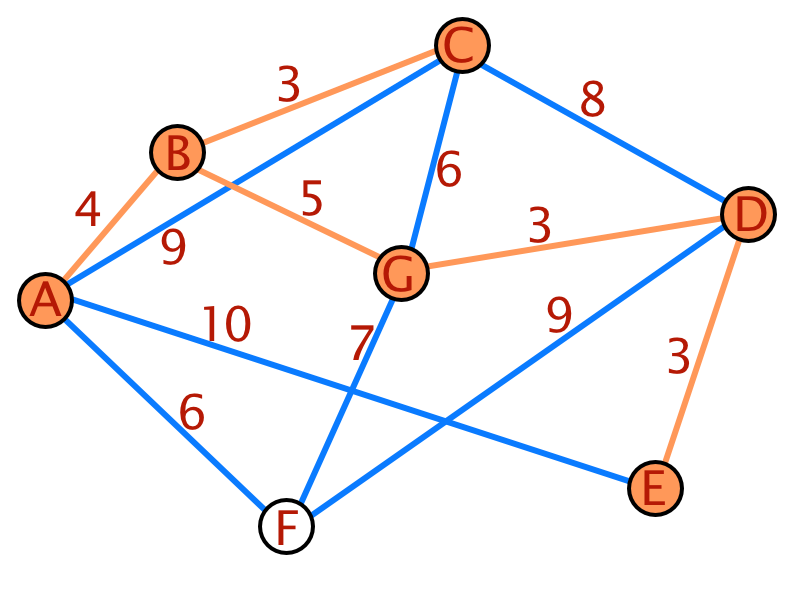
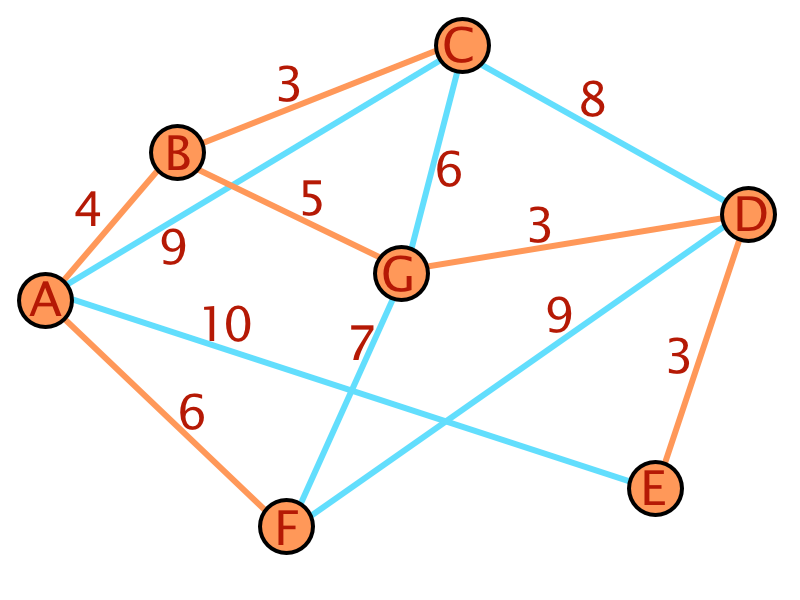
Auch hier soll wieder ein Beispiel des Algorithmus verdeutlichen.
Wir starten wieder mit dem bereits oben verwendeten Graphen und suchen einen Startknoten. |
 In diesem Beispiel wählen wir den Knoten A als Startknoten und betrachten die an A angrenzenden Kanten. |
 Die Strecke $\overline{AB}$ ist die kürzeste und folglich wird B in den Graphen eingebunden. Zur Menge der nun in Frage kommenden Strecken kommen die an B angrenzenden Strecken hinzu. |
 Aus der Menge der an A oder B angrenzenden (noch nicht verwendeten) Kanten ist die Strecke $\overline{BC}$ am kürzesten und wird hinzugefügt. Ebenso sind nun die an C angrenzenden Kanten zu mit betrachten. |
 Die nun kürzeste Strecke ist die Strecke $\overline{BG}$ und folglich wird G hinzugefügt. |
 Die nächste kürzeste angrenzende Strecke ist $\overline{GD}$ und wird hinzugefügt. |
 Fast vollständig ist der Spannbaum, wenn die jetzt kürzeste Strecke $\overline{DE}$ hinzugefügt wird. |
 Als letzte noch fehlende Strecke kommt die Strecke $\overline{AF}$ hinzu und vervollständigt den minimalen Spannbaum. |
Übungen
 | Greedy-Übungen.pdf (0.1 MB) |
| Greedy-Lösungen.pdf (0.2 MB) |
Literatur
- [1] Christian Wagenknecht: Algorithmen und Komplexität - Fachbuchverlag Leipzig, 2003 - ISBN 3-446-22314-2
- [2] Thomas H. Cormen, Charles E. Leiserson, Ronald Rivest, Clifford Stein: Algorithmen - Eine Einführung, Oldenbourg Verlag, 2. Auflage, 2007 - ISBN 978-3-486-58262-8
