Näherungsverfahren 1 SS10
Aus ProgrammingWiki

- Patrick Breite (sipabrei@stud.hs-zigr.de)
- Marcel Mücke (simamuec@stud.hs-zigr.de)
Inhaltsverzeichnis |
Einführung
Das Thema der Effizienten Näherungsalgorithmen baut zum teil auf andere Themenkomplexe auf,die sehr zu empfehlen sind:
Greedy-Algorithmen
Probabilistische Algorithmen
P-NP-Problem
Heuristiken
Begriff
Der Begriff Heuristik ist aus dem altgriechischen Wort "heuriskien" abgeleitet und bedeutet so viel wie "(auf)-finden" bzw. "entdecken".
Im 4. Jahrhundert entwickelte der griech. Mathematiker Pappos von Alexandria bestimmte Methoden die den heutigen Heuristiken stark ähneln:
- Betrachte das Problem als gelöst
- Lösungssuche durch Rückwärtsschreiten (Analyse)
- Beweis durch Vorwärtsschreiten (Synthese)
Das Gegenteil zu den Heuristiken ist die sogenannte Brute-Force-Methode, bei der alle möglichen Kombinationen durchgegangen werden. Dieses Verfahren wird hauptsächlich zum "Knacken" von Passwörtern verwendet.
Motivation
Von den NP-vollständigen Problemen gibt es eine Reihe bei der die Lösung von großem Interesse sind. Da aber keine Algorithmen zum vollständigen Lösen existieren, bedient man sich in der Praxis bestimmter Heuristiken, die zumindestens approximative (näherungsweise) Lösungen bieten.
Anwendungsgebiete
Wirtschaftswissenschaften
Im Bereich der Unternehmensforschung werden Heuristiken verwendet wenn der Rechenaufwand durch die enorme Anzahl der Möglichkeiten zu enorm ist. Beispiele dafür sind z.b. das beladen von Cotainerschiffen oder auch das bekannte Problem des Handlungsreisenden (TSP).
Philosophie
In der Philosophie spricht man von Heuristiken wenn etwas aufgrund großer Ähnlichkeit mit etwas anderem verglichen wird um das Verständnis dafür zu vertiefen. Beispiele dafür sind Gleichnisse, Metaphern und Fabeln.
Psychologie
In komplexen Situationen, in denen nur wenige Informationen zur Verfügung stehen, wird durch evolutionäre und erlernte Verfahren
einfache Regeln angewendet und versucht Probleme zu lösen bzw. die Lage zu beurteilen.
Im Bereich der Wahrnehmung findet man bestimmte Heuristiken die durch das Gehirn bestimmte Bilder rekonstruieren. Der Bereich der künstlichen Intelligenz zeigt die enorme Leistungsfähigkeit dieser.
Mathematik
In der Mathematik werden heuristische Verfahren einerseits zur Lösung von teilweise recht einfachen, jedoch zeitintensiven Problemen wie dem berechnen der Nullstellen von Polynomfunktionen und andererseits werden sie verwendet als sogenannte Eröffnungsverfahren um für bestimmte Probleme in möglichst kurzer Zeit und bei geringem Rechenaufwand eine Basislösung zu erhalten, welche durch Modifikationen und mehrfaches Ausführen präzisiert werden kann und zwar dennoch keine Optimallösung darstellt, jedoch dies auch bei einigen Problemen aufgrund des extrem hohen Zeitaufwandes nicht praktikabel ist und daher gern auf Heuristiken zurückgegriffen wird. Ein Beispiel für die Anwendung einer solchen Heursitik ist zum Beispiel das Matrixminimumverfahren, welches zur Lösung des TSP genutzt werden kann.
Informatik
Heuristiken werden in der Informatik hauptsächlich genutzt um mit möglichst geringem Rechenaufwand ein meist recht komplexes Problem zu lösen und eine zwar nicht optimale, aber dennoch zulässige Lösung zu erhalten. Es wird also im gegensatz zu anderen Algorithmen nicht garantiert, dass eine optimale Lösung errechnet wird, wodurch sich der Rechenaufwand und die somit benötigte Zeit meistens stark reduzieren und manchmal sogar fast minimieren. Bekannte Heuristiken sind zum Beispiel Simulated annealing und Greedy-Heuristiken, wie zum Beispiel die Nearest neighbour heuristic oder die Farthest insertion heuristic.
Springerproblem
Erläuterung des Springerproblems
Vor mehr als 200 Jahren formulierte der Schweizer Mathematiker Leonhard Euler erstmals das Problem des Rösselsprungs, auch Springerproblem genannt:
"Gibts es für einen Springer einen Weg, der jedes Feld eines n x n-Schachbrettes genau einmal besucht?"
Um diese Problem lösen zu können, muss bekannt sein, dass ein Springer eine Schachfigur ist, welche von ihrem aktuellem Feld zu einem Feld
bewegt werden kann, wobei zu beachten ist das entweder
und
oder
und
für die Bewegungen des Springers gelten muss.
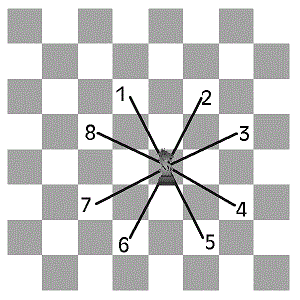
Auf dem folgenden Bild sind die möglichen Züge eines Springers zu erkennen.
.
Lösung mit Backtracking
Lange Zeit war für die Lösung des sogenannten Rösselsprungs nur der Naive Algorithmus mit Backtracking bekannt, wodurch ein Exponentieller Aufwand Zeitaufwand entsteht. Der Versuch mit diesem Algorithmus eine Lösung für ein n x n-Schachbrett mit zu finden ist nur mit enormem Zeitaufwand zu lösen, da bei einem 8 x 8-Schachbrett bereits über 3 Milliarden Züge überprüft werden müssten um mit einem reinen Backtracking Algorithmus zum Ziel zu gelangen.
Ein Applet welches mit einem Backtracking Algorithmus und verschiedenen anderen Algorithmen arbeitet um den Zeitaufwand zu verringern finden sie hier. Es ist zu beachten dass in diesem Algorithmus bestimmte Sackgassen schon vor dem Programmstart ausgeschlossen werden, um die Lösung dieses 8 x 8-Schachbretts in einer möglichst kurzen Zeit zu gewährleisten.
Warnsdorff Heuristik
Die Warnsdorff Heuristik wurde 1823 von H.C. Wanrsdorff entwickelt und der Grundgedanke ist, dass Felder mit wenigen Folgefeldern schnell isoliert werden und so nicht mehr besucht werden können.
Warnsdorff entwickelte desshalb folgende Regeln:
1. Ziehe auf das Feld mit der geringsten Zahl an noch zu erreichenden unbesuchten Folgefelder.
2. Wenn 2 oder mehr Felder die selbe Anzahl an noch zu erreichenden unbesuchten Folgefelder aufweisen ziehe auf das Feld, welches zuletzt (oder zuerst) betrachtet wurde.
Wenn man Beispielsweise die 1. Regel auf ein anwendet auf ein noch leeres Schachbrett sieht dies folgendermaßen aus:
Die Heuristik von Warnsdorff garantiert jedoch nur eine näherungsweise Lösung des Springerproblems, da bei größeren Schachbrettern nicht alle Sackgassen gemieden werden, was für Warnsdorff unmöglich zu untersuchen war, da er noch keine Computer zur Verfügung gehabt hat, welche diese Springertour auf beispielsweise einem 80x80 großem Schachbrett errechnen.
Weiterhin kann man zeigen, dass es für Schachbretter der Größe keine Lösungen existieren, da der Springer immer in einer Sackgasse landet, egal von wo er startet. Sie können dies auch in dem unten verlinktem Java Programm austesten.
Einen kurzen Algorithmus, zur Lösung des Springerpoblems mit der Warnsdorff Heuristik, finden Sie in diesem Java Programm und ebenfalls ist dieses Applet zu empfehlen, wenn man selbst einen Weg für das Springerproblem finden möchte und um den Weg des Springers vielleicht besser nachvollziehen zu können.
Modifikationen der Warnsdorff Heuristik
Es ist möglich eine Heuristic zu modifizieren um eventuell eine Verbessserung zu erreichen, jedoch kann man bei Heuristiken nur sehr schwer nachweisen in wieweit die Heuristik sich verbessert hat, da sehr umständliche und komplizierte Tests durchgeführt werden müssen.
Nun einige Modifikationen der Warnsdorff Heuristik:
1. Wähle nicht das zuletzt/zuerst betrachtete Feld mit dem geringsten Feldwert, sondern das zuerst/zuletzt betrachtete Feld.
2. Wähle bei gleichwertigen Feldwerten die Felder mit den geringsten Feldwerten und bei einer Dopplung wähle eines zufällig aus.
3. Wähle das Feld, das die größte Summe aller Feldwerte der möcglichen Foldefelder hat.
4. Wähle das Feld, das am weitesten vom Brettrand entfernt ist, also in Zentrumsnähe liegt.
Algorithmus von Axel Conrad
1992 entwickelte eine Schülergruppe im Rahmen des Bundeswettstreits für Informatik, einen Algorithmus für die Lösung des Springerproblems in .
Der Conrad-Algorithmus ist nach einem seiner Erfinder Axel Conrad benannt und stützt sich auf das Prinzig von Teile und Herrsche auf. Der Conrad-Algorithmus
schafft es ein Schachbrett beliebiger Größe exakt zu lösen und zwar indem man ein 5x5 große Teile zerlegt. Wenn die Seitenlänge des Schachbretts kein Vielfaches von 5 ist, entstehen L-förmige Teilbretter am Rand und in der Mitte ergibt sich ein 6x6 oder 9x9 großes Feld. Da es möglich ist von einem dieser kleineren Teile in einen anliegenden zu springen kann man so alle einzelnen kleineren Schachbretter durchqueren und eine Springertour finden. Bei der Entwicklung dieses Algorithmus von Axel Conrad und seinen Mitschülern entstand ein Algorithmus mit dem sich sogar für ein Schachbrett der Größe 100.000.000 x 123.456.789 innerhalb einer Sekunde eine Spingertour berechnen lässt. Axel Conrad gibt auf seiner Website unter anderem auch eine Lösung für nicht quadratische Schachbretter an. Axel Conrad und Diana Schmied gelang es sogar im Jahr 1998 einen Algorithmus zu entwickeln, welcher in der Lage ist ein dimensionales Schachbrett zu lösen.
Ein sehr schönes Programm von Daniel Flex und Steffen Lehmann aus der IIB07, das alles nocheinmal schön zusammenfasst finden Sie unter diesem Link.
Lokale Suche
Verzweigen und Begrenzen
Der ihnen schon bekannte branch and bound Algorithmus (siehe Verzweigen und beschränken SS10) wird folgendermaßen abgewandelt:
1. Anstatt die eigentliche Schrankenfunktion zu berechnen wird diese durch eine mehr oder weniger grobe Schätzfunktion ersetzt
2. Die Bound-Berechnung entfällt -> man akzeptiert also, dass nicht wirklich eine Schranke berechnet wurde
Das Ergebnis ist ein Näherungsalgorithmus, dessen Ergebnis zwar vom Optimum abweichen wird, jedoch kann man in den meisten Fällen sagen, dass die Ergebnisse zufriedenstellend bis gut sind, also in der Regel eine kaum nennenswerte Abweichung vom Optimums aufzeigen.
Greedy-Heuristiken
Der Unterschied zwischen einer Greedy-Heuristik und einem Greedy-Verfahren ist hauptsächlich die Qualität der Lösungen, da ein Greedy-Verfahren eine exakte Lösung und eine Greedy-Heuristik nur eine Näherungslösung, welche jedoch in den meisten Fällen recht nah an der exakten Lösung liegt, liefert. Ein Greedy-Verfahren benötigt, anders als eine Greedy-Heuristik, zur Angabe einer exakten Lösung ein Matroid als zugrunde liegende algebraische Struktur. Es ist beispielsweise beim Bruchteil-Rucksackproblem der Fall, dass die zugrunde liegende algebraische Struktur ein Matroid ist, jedoch nicht beim 0/1-Rucksackproblem. Wendet man trotz dem nicht vorhandenem Matroid beim 0/1-Rucksackproblem ein Greedy-Verfahren an, so erhält man eine Näherungslösung und man spricht dann von einer Greedy-Heuristik.
Greedy-Heuristiken zeichnen sich dadruch aus, dass sie immer nach einem lokalem Optimum suchen und weder bereit sind eine Entscheidung zu revidieren noch eine lokale Verschlechterung zu ermöglichen.
Wenn man zum Beispiel eine Greedy-Heuristik zur Lösung des TSP verwenden möchte so wird man versuchen gerade den Knoten einzubinden, der den größten Gewinn, also hier die kürzeste Rundreise beschert. Beispielsweise könnte man auf die Idee kommen immer den Knoten einzubinden, welcher dem gerade betrachteten am nächsten liegt. Diese Strategie nennt man nearest neighbor heuristic. Sie ist jedoch in den meisten Fällen nicht wirklich hilfreich, da die Ergebnisse meist unbrauchbar sind oder zumindest ziemlich weit vom Optimum abweichen. Bessere Resultate erhält man zum Beispiel mit der farthest insertion. Bei der farthest insertion beginnt man die Knoten mit dem geringstem Abstand zu verbinden oder man erstellt einen Konvexe Hülle (eine Erläuterung findet man hier) und erweitert die Tour dann um den Knoten, dessen Minimalabstand zu einem bereits auf der Rundreise liegendem Knoten maximal ist. Diese Technik führt zu ebenso guten Ergebnissen wie die random insertion, bei der ein unbenutzter Knoten zufällig ausgewählt wird und so integriert wird, dass die daraus resultierende Länge der Rundreise minimal wird. Ein weiteres Greedy-Verfahren ist die nearest insertionoder auch cheapest insertion genannt. Bei diesem Verfahren wird der Knoten eingebunden, der die geringste Verlängerung der daraus resultierenden Teilroute zur Folge hat.
Es wurde mitlerweile bewiesen, dass größere Schritte besser sind als kleine, desshalb werden also anstelle kleine Veränderungen beim TSP zu betrachten möglichst große gewählt. Dies führt zu einem weiteren Greedy-Verfahren, der best insertion. Bei diesem Verfahren geht man vor wie bei einem Bombenabwurf, es werden in einem kreisförmigen Gebiet alle Städte zerstört und dann nacheinander wieder aufgebaut, wobei man sie mittels der Farthest-Insertion-Methode in den Rundweg integriert, was best insertion genannt wird. Nach diesem Verfahren aus dem Ruin-and-recreate-Bereich ist die entstandene Länge des Rundweges im allgemeinen kürzer als vorher.
Zwei schöne Applets für Greedy Heuristiken finden sie auf dieser Seite von Stephan Mertens.
Hill climbing
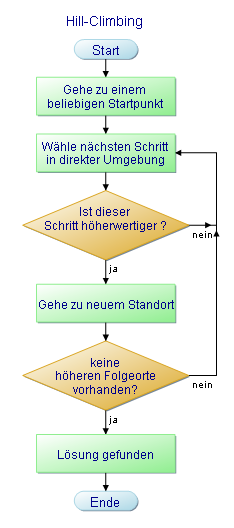
Beim Hill-Climbing, auch Bergsteigeralgorithmus genannt, wird von einer beliebigen Startlösung aus versucht aus den in der nähe befindlichen Lösungen die bessere auszuwählen, bis keine Verbesserung mehr möglich ist.
Am Beispiel eines Bergsteigers bedeutet dies, das ein Bergsteiger auf einer beliebigen Postion in der Landschaft immer Versucht eine höhere Position zu erreichen. Dabei wird auch schnell der Schwachpunkt des Hill-Climbing-Algorithmus ersichtlich, denn er endet oft in einem lokalen Maximum. Bezogen auf den Bergsteiger bedeutet dies, wenn zwischen seiner aktuell höchsten (lokalen) Position und einer höheren (globalen) Position ein Tal liegt, hat er somit keine Möglichkeit diese zu erreichen.
Das Problem kann aber mit verschiedenen Ansätzen minimiert werden:
- mehrmaliges Ausführen der Methode
- mehrere Bergsteiger mit verschiedenen Startpunkten
- zufällige große Sprünge und danach erneutes Anwenden der Methode
Threshold accepting
1990 veröffentlichten Dueck und Scheuer ihr Buch über die Schwellenakzeptanz (Threshold accepting: a general purpose optimization algorithm appearing superior to simulated annealing). Der Threshold accepting Algorithmus befasst sich hauptsächlich damit einen gewisse Tolleranzgrenze einzurichten um mögliche zwischenzeitliche Verschlechterungen zu ermöglichen, was zu besseren Näherungslösungen führen kann. Man würde also überprüfen, ob eine lokale Veränderung nach einer Bewertung um mehr als
von der vorhergehenden Lösung abweicht und sie verwerfen insofern dies der Fall ist. Es wird somit zu anfang ein
gewählt welches möglichst groß ist, wobei auch ein
gewält werden kann durch welches anfangs kaum Beschränkungen entstehen, da wenn über längere Zeit keine Verbesserungen eintretetn
langsam auf null gesenkt wird. Der Nachteil ist, dass wenn zum Beispiel der Bergsteiger aus dem zuvor beschriebenem Problem beim hill-climbing einen Nebengipfel erreicht hat und
bereits gesenkt wurde, so gibt es keine Möglichkeit für den Bergsteiger den höchsten Gipfel zu erreichen.
Der Unterschied zum simulated annealing besteht in der Behandlung der Verschlechterungen bei den neuen gegenüber den alten Lösungen.
Während beim simulated annealing mit einer bestimmten berechneten Wahrscheinlichkeit entschieden wird ob eine Verschlechterung akzeptiert wird oder nicht, wird beim threshold accepting jede Verschlechterung akzeptiert solange sie nicht überschreitet.
Durch das wegfallen einer komplexen Berechnung für die Zufallszahl und die Exponentialfunktion ergibt sich ein besseres Laufzeitverhalten in Bezug auf die Geschwindigkeit. Beim threshold accepting können in der gleichen Zeit mehr Lösungen durchprobiert werden und gleichzeitig liefert er meist qualitativ bessere Lösungen.
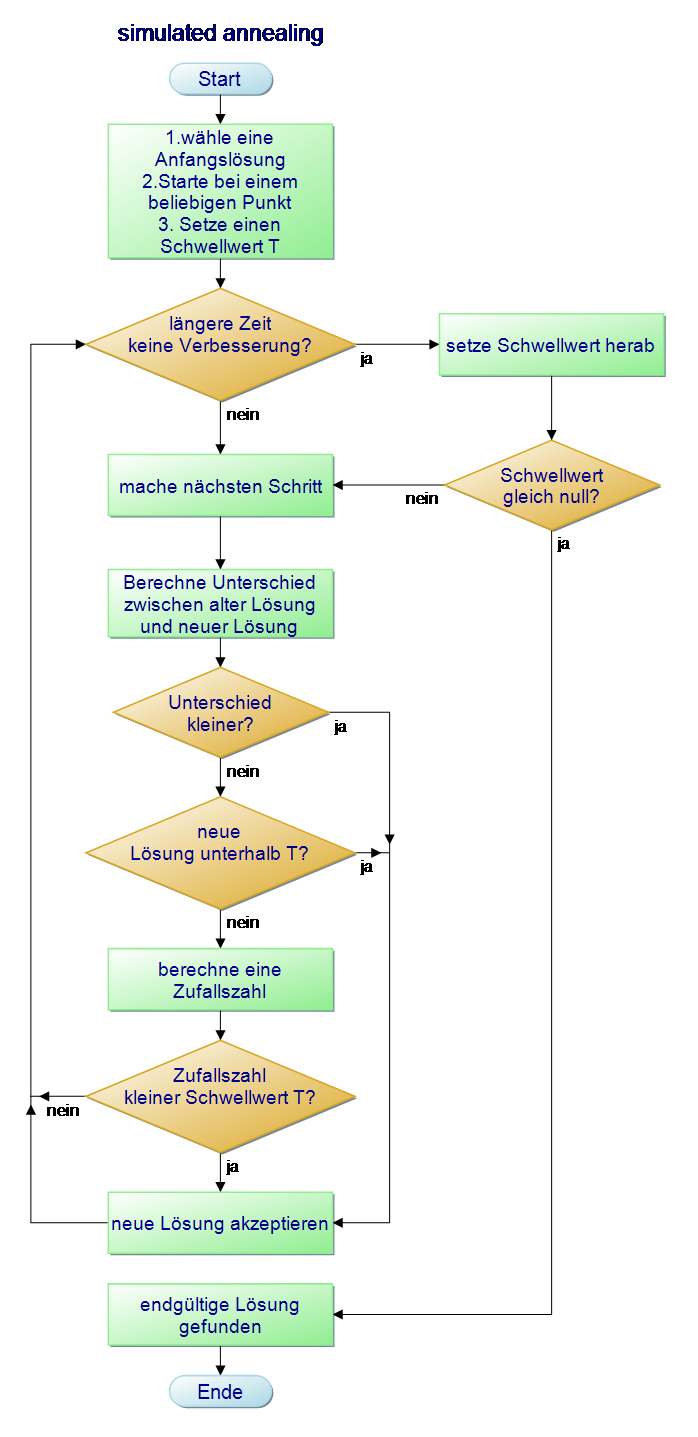
Simulated annealing
Die Herren Scott Kirkpatrick, Charles D. Gelatt und Mario P. Vecchi vom IBM-Forschungszentrum Yorktown Heights entwickelten 1983 das sogenannte simulated annealing, was übersetzt simuliertes langsames Abkühlen bedeutet.
Dieses Verfahren wird hauptsächlich in der Werkstofftechnik eingesetzt. Bei diesem Verfahren werden Metalle erhitzt und dabei werden die atomaren Teilchen aus ihrer festen Gitterstruktur gelöst. Beim langsamen abkühlen verbinden sich die Teilchen wieder zu einer festeren und geordneteren Gitterstruktur. Dadurch erhält man Metalle mit verbesserten Eigenschaften(weniger Unregelmäßigkeiten in der Struktur). Zur Herstellung von Mikroprozessoren und Speicherbausteinen werden z.B. Materiallien wie Silizium benötigt welche keine Unregelmäßigkeiten besitzten.
Der Algorithmus baut auf dem sogenannten Metropolisalgorithmus auf, der 1953 von Nicholas Metropolis et al. publiziert wurde. Der Metropolisalgotithmus ist eine Monte-Carlo-Methode (siehe Probabilistische Algorithmen) zur Erzeugung von Zuständen eines Systems basierend auf der Boltzmann-Verteilung. Im Gegensatz zum treshold accepting wird trotz Überschreiten der festen Toleranzschwelle mit einer bestimmten Wahrscheinlichkeit, mittels Zufallszahl und Exponetialfunktion, zufällig entschieden, den Lösungsvorschlag doch zuzulassen. Diese Wahrscheinlichkeit richtet sich nach der Größe der Überschreitung von
. Sehr große Überschreitungen werden dabei deutlich seltener zugelassen als kleinere.
Beim simulated annealing wird nun zusätzlich noch immer weiter abgesenkt. Dieses Verfahren wir hauptsächlich dazu benutzt ein globales Minimum zu finden. Bezogen auf das beispiel des Bergsteigers bedeutet dies, das er nun versucht in das tiefste Tal hinabzusteigen. Dabei kann es passieren das der Bergsteiger sich in einem lokalen Minimum (Tal) verfängt und erst wieder durch eine große Überschreitung von
frei kommt.
Das untere Video verdeutlicht nochmal die Arbeitsweise des Algorithmus.
Tabu-Suche
Der Algorithmus der Tabu-Suche wurde von Fred Glover entwickelt und erfährt seitdem immer wieder Verbesserungen.
Die zugrunde liegende Idee basiert darauf, dass es bei den oben genannten Algorithmen (treshold accepting und simulated annealing) vorkommen kann das ein oder mehrere Schritte rückgängig gemacht werden. Um dies zu vermeiden werden die vorangegangen Lösungen bzw. Schritte in einer sogenannten Tabu-Liste gespeichert, die mehrere Warteschlangen implementieren kann. Stimmt ein neuer Schritt mit einer Lösung in der Tabu-Liste überein, wird er verworfen und es muss eine neue Lösung gefunden werden, die noch nicht in der Tabu-Liste vorhanden ist.
Ein passendes Java-Applet zum besseren Verständnis befindet sich hier.
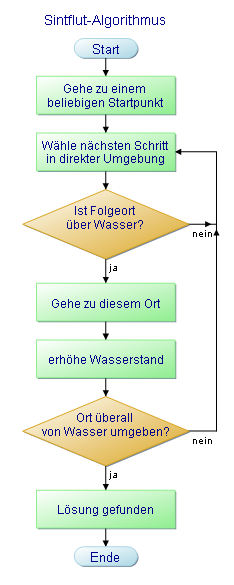
Sintflut-Algorithmus
Der Sintflutalgorithmus wurde 1993 von Gunter Dueck und Tobias Scheuer bei der Firma IBM in Heidelberg entwickelt.
Er ist eine Weiterentwicklung bzw. Vereinfachung des weiter oben beschriebenen "Simulated Annealing"-Algorithmus und hat im Gegensatz zu den Treshold-accepting-Verfahren keinen Schwellwert der für jeden Schritt vorgegeben ist sondern eine globale untere Schranke die sich langsam aber stetig erhöht. Dabei spielt es keine Rolle, ob der nächste Schritt näher oder weiter entfernt von der Lösung gegenüber dem vorigen Schritt liegt, solange die globale Schranke nicht unterschritten wird. Im laufe des Prozesses wird dadurch die Anzahl der möglichen Schritte immer weiter eingeschränkt, bis keine Schritte mehr möglich sind und das gesuchte Optimum der Lösung gefunden ist.
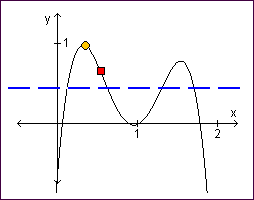
Am besten lässt sich dies am Beispiel des Bergsteigers erklären, der sich versucht während einer steigenden Flut auf den in seiner Umgebung befindlichen höchsten Punkt zu retten. Der höchste Punkt bzw. Gipfel ist dabei das gesuchte Optimum. Während der Wasserstand immer weiter steigt ist der Wanderer ständig in Bewegung. Er merkt er sich dabei den höchsten Punkt den er bisher erreicht hat. Es ist ihm möglich jeden Gipfel und jedes Tal zu beschreiten, solange er sich über der Wasserlinie bewegt. Ist er komplett von den Wassermassen umgeben und kein Schritt mehr möglich, hat er den höchsten lokalen Punkt erreicht.
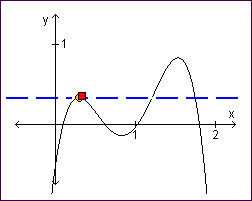
Die untere Abbildung zeigt die Anwendung im 2-dimensionalen Raum, wobei der rote Punkt den Wanderer, der gelbe Punkt den bisher höchsten lokalen Punkt und die blaue Linie den aktuellen Wasserstand darstellen.
Ein passende Java-Applet befindet sich hier.
Der Sintflut-Algorithmus arbeitet, wie auch treshold accepting, im Gegensatz zum simulated annealing deterministisch.
Bei geschickter Implementierung arbeiet er etwas schneller als die beiden anderen Verfahren, wobei er in der Qualität seiner Lösungen nicht ganz so stabil ist. Dieser vermeintliche Nachteil ist einfach zu erklären.
Wird die Schrittgröße des Wanderers zu groß gewählt, kann es passieren das er mit einem einzigen Schritt den Gipfel überspringt. Ist die Schrittgröße stattdessen zu klein, steigt das Wasser zu schnell um möglichst viele verschiedene Punkte zu beschreiten. Das bedeutet das der Algorithmus stark von der Schrittgröße abhängig ist. Des Weiteren kann es passieren das der Wanderer auf einem niedrigeren Gipfel(lokales Maximum) von den Wassermassen eingeschlossen wird und damit keine Möglichkeit mehr hat auf den höheren Gipfel(globales Maximum) zu gelangen.
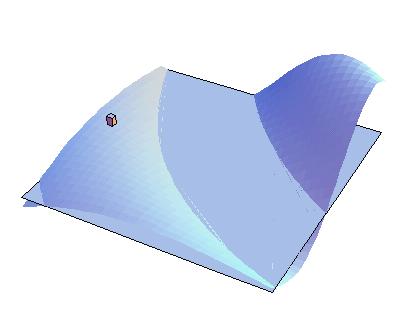
Dieser Nachteil wird mit steigender Anzahl der Dimensionen verkleinert. Schon bei der Anwendung im 3-dimensionalen Raum ergeben sich für den Wanderer mehr Möglichkeiten sich zu bewegen. Anstatt nur nach rechts oder links zu gehen kann er sich nun ebenfalls nach vorn und nach hinten bewegen, wobei auch hier die Wahrscheinlichkleit nur ein lokales Maximum zu erreichen vergleichsweise hoch ist. Die eigentliche Anwendung des Sintflut-Algorithmus liegt aber sowieso hauptsächlich im hochdimensionalen Raum mit 100 Dimensionen und mehr z.b. beim TSP.
Zum Abschluss nun noch die Möglichkeit ein sehenswertes Video von Tobias Scheuer, das den Sintflut-Algorithmus einfach und verständlich erklärt anzuschauen. Dieser Link ist aber irgendwo auf dieser Seite versteckt (kleiner Hinweis: Am besten immer direkt auf den Punkt kommen.) Viel Spass beim entdecken, es lohnt sich.
Fazit
Man kann sagen, dass Heuristiken in den meisten Fällen zwar keine Optimalen Lösungen zurückgeben, aber da meistens die Lösungen nur sehr geringfügig von einem Optimum abweichen und desshalb sehr nützliche Hilfsmittel sind um bei extrem komplexen Problemen mit möglichst kleinem Aufwand eine gute bis fast Optimale Lösung zu erhalten.
Übungsaufgaben
1. Entwerfen Sie für den treshold-accepting-algorithmus einen Programmablaufplan mithilfe des kostenlosen Programmes PapDesigner(Bitte nur die gepackte exe herunterladen, da nur diese auf den Hochschulrechner ohne Admin-Rechte funktioniert).
2. Überlegen Sie wie man es erreichen kann, dass beim verwenden der Warnsdorff-Heuristik bei der gleichen Startposition unterschiedliche Wege für den Springer entstehen und verändern Sie die Methode "findeBestenWeg" in diesem Programm.(Also bitte die 2. Modifikation im Java Programm impelementieren)
 | Sipabrei_AuK_Übung_norm.zip (0.1 MB) |
3. Experimentieren Sie mit den verlinkten Applets über die Greedy-Heuristiken und das Springerproblem
Quellen
Literatur
- [1] Christian Wagenknecht
- Algorithmen und Komplexität,- Fachbuchverlag Leipzig, 2003.- ISBN 3-446-22314-2
- [2] Doina Logofatu
- Grundlegende Algorithmen mit Java - Vom Algorithmus zum fertigen Programm: Lern- und Arbeitsbuch für Informatiker und Mathematiker ,- Verlag Vieweg+Teubner, 2007.- ISBN 3834803693
Weblinks
[1] Wikipedia Heuristik
[2] Wikipedia Tabu-Suche
[3] Wikipedia hill climbing
[4] Construction Heuristics
[5] fh-friedberg Sintflut
[6] www.omnisophie.com
[7] www.siebn.de
[8] Axel Conrad