Dynamisches Programmieren SS09

Aus ProgrammingWiki

Autoren:
Markus Ullrich - simaullr@stud.hs-zigr.de
Norbert Baum   - sinobaum@stud.hs-zigr.de

Inhaltsverzeichnis

1 Eigenschaften
2 Iterative Berechnung
3 Rekursive Berechnung
4 Optimale Teilstruktur
5 Beispiele
- 5.1 Fibonacci-Zahl
  - 5.1.1 ohne memoizing
  - 5.1.2 mit memoizing
- 5.2 Rundreiseproblem
6 Aufgaben
7 Files
- 7.1 Vortragsfolien
- 7.2 Lösungen zu den Aufgaben
8 Links
9 Literatur

Eigenschaften

Eine Sache vorweg:

Der Begriff "Programmierung" bezieht sich in diesem Kontext nicht auf das schreiben von Code , sondern vielmehr auf eine tabellarische Methode zum Lösen von Optimierungsproblemen. Demnach sollte die Methode besser "Dynamisches Optimieren" heißen, was jedoch die traditionelle Bezeichnung nicht mehr verdrängen kann.

Im folgenden werden nun zunächst die Eigenschaften dynamischer Programmierung erläutert.

Bottom-up

Genau wie die Teile-und-Herrsche-Verfahren, löst auch die Dynamische Programmierung Probleme, durch die Kombination der Lösungen von Teilproblemen. Allerdings nutzt die dynamische Programmierung einen Bottom-up-Ansatz, bei dem alle Teillösungen "von unten her" berechnet werden. Die bereits berechneten Teillösungen werden in einer Tabelle gespeichert, womit deren erneute Berechnung entfällt. Dabei wird erwartet, dass eine optimale Gesamtlösung aus optimalen Teillösungen aufgebaut werden kann. Eine solche Lösung sollte bewusst nicht als die optimale Lösung bezeichnet werden, da es verschiedene Lösungen geben kann, die den optimalen Wert besitzen.

Schwierigkeiten

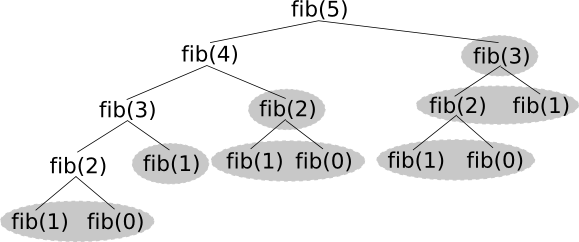
Wenn nun aus der rekursiven Beschreibung eine optimale Lösung ebenfalls rekursiv erstellt werden soll, stoßen wir auf das Problem, dass wir selten unabhängige und überlappungsfreie Teilprobleme erhalten. Das wird schon deutlich wenn wir uns die Berechnung von $fib(5)$ ansehen. Dabei müssen bei einer rekursiven Lösung erheblich viele Teilprobleme mehrfach berechnet werden. Im Bild sind diese Probleme grau hervorgehoben, ebenso wie $fib(1)$ und $fib(0)$ , da diese bekannte Werte sind die ohnehin nicht 'berechnet' werden müssen.

Weiterhin kann es passieren das die zu lösenden Teillprobleme unausgewogen sind. Das bedeutet, dass ein besonders schwierig zu lösendes Teilproblem den Erfolg der ganzen Methode zunichte macht. Ein populäres Beispiel vom Schach ist das Springerproblem oder auch Rösselsprung genannt. Dabei geht es darum, dass ein Springer jedes Feld auf einem beliebig großen Schachbrett genau einmal besucht. Eine mögliche Lösung unterteilt das Schachbrett in kleinere Teilrechtecke, für die spezielle Lösungen existieren. Dabei können aber verbleibende Rechtecke erheblich schwerer zu lösende Teilprobleme darstellen, zudem gewisse Anschlussbedingungen zwischen den Rechtecken realisiert werden müssen. Wer sich näher für das Problem interessiert, dem wird folgende Seite empfohlen: Springerproblem.

Da bei dynamischer Programmierung alle Teilprobleme berechnet werden kann eine sehr große Anzahl dieser ebenfalls zum Problem werden. Zudem ist nicht bei jedem Problem garantiert, dass aus der Kombination der optimalen Teillösungen eine optimale Gesamtlösung entsteht.

Überlappende Teilprobleme

Wie bereits bekannt finden wir selten Probleme, die aus unabhängigen Teilproblemen bestehen und somit eine rekursive Lösung einen erheblichen Mehraufwand betreiben würde. Die Anwendung Dynamischer Programmierung macht jedoch vor allem in solchen Fällen Sinn, also wenn Teilprobleme ihrerseits gemeinsame Teilprobleme nutzen. Dabei entfällt die erneute Berechnung von Teilproblemen, da deren Lösungen ja in einer Tabelle gespeichert werden. Wenn man sich das Beispiel der Berechnung von $fib(5)$ ansieht, kann man sehr gut erkennen, dass somit die Berechnung von fib(n-2) komplett entfallen kann, da der Wert bereits durch die Berechnung von $fib(n-1)$ bekannt ist.

Der damit eingesparte Zeitaufwand sollte dabei natürlich über dem zeitlichen Mehraufwand durch die Berechnung aller nicht benötigten Teilprobleme liegen. Das ist beim Beispiel der Berechnung der Fibonacci-Zahlen immer der Fall, da sämtliche Teilprobleme zur Berechnung benötigt werden.

Iterativ oder rekursiv?

Unseren Überlegungen zufolge wäre es also nicht von Vorteil einen rekursiven Lösungsansatz zu verwenden, da eine rekursive Lösung ineffizienter ist und somit der rekursive Lösungsansatz erst in eine iterative Lösung übertragen werden muss. Dabei ist ein erheblich hoher Denkaufwand zu leisten der somit auch in hohem Maße fehleranfällig ist.

Aber gibt es eine Möglichkeit die Effizienz einer rekursiven Lösung zu steigern, und zwar: memoizing.

Dabei werden die rekursiv berechneten Teilprobleme, wie bei einem iterativen Ansatz in einer Tabelle zwischengespeichert. Vor der Berechnung eines Teilproblems wird nun zunächst in dieser Tabelle nachgeschlagen ob bereits eine Lösung vorhanden ist. Ist dies der Fall kann die erneute Berechnung entfallen. Wenn nicht, so wird der gesuchte Wert berechnet und danach in die Tabelle eingetragen.

Somit können wir also doch einen rekursiven Lösungsansatz verwenden. Da dafür erheblich weniger Denkaufwand zu leisten ist, ist somit unsere Lösung weniger fehleranfällig.

Im folgenden werden nun iterative und rekursive Lösungen am Beispiel des bereits bekannten Rucksackproblems verglichen.

Iterative Berechnung

Von iterativer Berechnung spricht man dann, wenn ein schrittweiser Zugriff/Ablauf/Berechnung zum Einsatz kommt. Durch den Top-Down-Ansatz werden auch Teilberechnungen/Teilprobleme berechnet, die eventuell nicht benötigt werden. Aber es kommt zu keiner Mehrfachberechnung.

Beim Rucksackproblem werden die Zellen der Tabelle schrittweise ausgerechnet und befüllt, deswegen sprechen wir auch bei der ersten Lösung von der Iterativen Lösung des Rucksackproblems.

Rückkehr des Rucksackproblems

Das Rucksackproblem wurde zwar in den verschiedenen Kapiteln schon einmal angesprochen, aber wir werden es trotzdem noch einmal kurz erklären. Es ist auch unter dem Namen Knapsack problem, Transportproblem oder einfach nur Rucksack bekannt. Dabei handelt es sich um ein bekanntes Optimierungsproblem der Kombinatorik.

Der Name Transportproblem ist schon sehr gut gewählt. Das Ziel ist es, $n$ Gegenstände einzupacken/zu transportieren, wobei jeder Gegenstand ein Gewicht/Volumen und einen Wert hat. Dabei sollen die $n$ Gegenstände so kombiniert werden, dass der Wert aller eingepackten Gegenstände maximal ist, jedoch darf das Gewicht/Volumen nicht überschritten werden.

Dieser Algorithmus oder dieses Optimierungsverfahren findet Anwendung in der Beladung von LKWs, Schiffen - überall dort, wo man einen maximalen finanziellen Gewinn erwirtschaften will.

Bei der Dynamischen Lösung des Problems sollen nun die Probleme der rekursiven Lösung behoben werden. Wie schon erwähnt, werden Teilprobleme/Teilberechnungen eventuell doppelt durchgeführt. Mithilfe der Dynamischen Optimierung/Programmierung tritt dies nun nicht mehr auf. Vor der Lösung eines Teilproblems wird erst einmal geschaut, ob dies schon geschehen ist. Wenn 'Ja', dann wird die Lösung einfach abgerufen, wenn 'Nein', dann wird der neue Wert berechnet und dann in die Tabelle eingetragen.

Die folgende Formel zeigt erst einmal die rekursive Beschreibung der Lösung: $wert(i,g) = \begin{cases} 0, & wenn \ i =0 \\ wert(i-1, g), & wenn \ i > 0 \ und \ g-g_{i} < 0\\ max(wert(i-1,g), wert(i-1, g-g_{i})+w_{i}), & sonst \\ \end{cases}$

Dimension der Tabelle

Wie schon oben erwähnt, werden die Daten in einer Tabelle gespeichert. Ohne diese ist es nicht möglich eine iterative Berechnung durchzuführen, da die aktuelle Berechnung immer Werte von vorher gegenden Berechnungen benötigt. Diese baut sich aus den Gegenständen (= Anzahl der Zeilen) und der Kapazität (= Anzahl der Spalten) auf. Dabei ist zu beachten, dass die erste Spalte und auch die erste Zeile für die Initialisierung benötigt werden.

Obwohl in der heutigen Zeit genug Speicher zur Verfügung steht, beschränken wir uns darauf, nur 2 Zeilen, nämlich die aktuelle und die vorherige Zeile zwischen zu speichern. Das liegt Nahe, da auch nur die vorhergehende Zeile zur Berechnung der aktuellen benötigt wird.

Implementation

Die Umwandlung der rekursiven in eine iterative Berechnung ist nicht so trivial wie man eventuell denkt. Zum Ausfüllen der gesamten Tabelle müssen wir die rekursive Formel in zwei verschachtelte for-Anweisungen verpacken.

Prozedur: gesamtwertIterativ
Zweck: Rucksack Algorithmus zur Berechnung des maximalen Werts
Parameter: int kapazitaet
int-Array zeileAlt
int-Array zeileNeu
FOR i := 1 TO Anzahl der gegenstaende STEP 1 DO
 Kopiere die zeileNeu auf zeileAlt
 gi := das Gewicht vom dem aktuellen Gegenstand(i)
 FOR g := 0 TO kapazitaet STEP 1 Do
  wenn g < gi dann 
   zeileNeu[g] := zeileAlt[g] //zeileNeu erhält den Wert von zeileAlt an der Postition g
  sonst
   temp := zeileAlt[g-gi] + Wert von gegenstaend[i]
   zeileNeu[g] := Max(temp, zeileAlt[g]) //zeileNeu bekommt den max-Wert entweder temp oder den alten
  wenn_ende
 next
next

Ergebnis: zeileNeu[kapazitaet] // letzte Spalte im Array steht der Maximale Wert

Da wir keine eigenen Klassen verwenden können, haben wir uns zum Darstellen der Gegenstände für Objekte vom Typ 'Point' entschieden. Dabei stellt der X-Wert das Gewicht und der Y-Wert den Wert des Gegenstandes dar. Für den schnellen Zugriff verwenden wir eine Hashmap der Form HashMap<Integer,Point>.

Es stellt sich auch die Frage, woher man weiß, mit welchen Gegenständen man den maximalen Wert erreicht hat und demnach welche man nun einpacken muss. Dies haben wir durch eine 2. Tabelle gelöst. Diese ist genauso groß wie die erste. Jedoch werden dort nicht die Werte gespeichert, sondern die Reihenfolge der Gegenstände, die eingepackt wurden. In unserem Fall werden die Gegenstandsnummern in der Tabellen-Zelle gespeichert und durch ein ';' getrennt.

private java.util.HashMap gegenstaende = new java.util.HashMap(); gegenstaende.put(1, new java.awt.Point(13,19)); gegenstaende.put(2, new java.awt.Point(11,20)); gegenstaende.put(3, new java.awt.Point(17,23)); gegenstaende.put(4, new java.awt.Point(15,21)); gegenstaende.put(5, new java.awt.Point(16,27)); gegenstaende.put(6, new java.awt.Point(14,25)); gegenstaende.put(7, new java.awt.Point(18,25)); gegenstaende.put(8, new java.awt.Point(10,18)); gegenstaende.put(9, new java.awt.Point(19,24)); gegenstaende.put(10, new java.awt.Point(12,17)); public int[] iterativ(int kapazitaet) { int[] zeileAlt = new int[kapazitaet+1]; int[] zeileNeu = new int[kapazitaet+1]; String[] zeileAltG = new String[kapazitaet+1]; String[] zeileNeuG = new String[kapazitaet+1]; for(int z = 1; z <= gegenstaende.size();z++) { System.arraycopy(zeileNeu, 0, zeileAlt, 0, zeileNeu.length); System.arraycopy(zeileNeuG, 0, zeileAltG, 0, zeileNeuG.length); int gewicht = (int)gegenstaende.get(z).getX(); for(int s = 0; s <= kapazitaet; s++) { if(s >= gewicht) { int temp = zeileAlt[s-gewicht] + (int)gegenstaende.get(z).getY(); if(temp>zeileAlt[s]) { zeileNeu[s] = temp; if(zeileAltG[s-gewicht] == null) { zeileNeuG[s] = z+""; } else { zeileNeuG[s] = zeileAltG[s-gewicht] + ";" + z; } } } } } if(zeileNeuG[kapazitaet] != null) { String[] g = zeileNeuG[kapazitaet].split(";"); int[] back = new int[g.length]; for(int i=0; i<g.length; i++) { back[i] = Integer.parseInt(g[i]); } return back; } return null; }

public void printIterativ(int kapazitaet) { int[] inRucksack = iterativ(kapazitaet); int gesamt = 0; int wert = 0; for(int i = 0; i<inRucksack.length; i++) { int z = inRucksack[i]; int g = (int)gegenstaende.get(z).getX(); int w = gegenstaende.get(z).y; gesamt += g; wert += w; System.out.println("Gegenstand " + z + " ist im Rucksack"); } System.out.println("--------------------------"); System.out.println("Wert im Rucksack: " + wert); System.out.println("Gesamtgewicht: " + gesamt + " von " + kapazitaet); if(gesamt < kapazitaet) { System.out.println("Da ist ja noch Platz für n Stulle und was zutrinken ;)"); } }

printIterativ(120);

private void initCanvas(int kapazitaet) { canvas.clear(); canvas.line(20,0,20,200); canvas.line(0,20,1100,20); for(int i = 0 ; i <= kapazitaet ; i++) { canvas.text(30+i*25,15,""+i); } for(int i = 0 ; i <= kapazitaet ; i++) { canvas.text(30+i*25,35,"0"); } for(int i = 0 ; i <= gegenstaende.size() ; i++) { canvas.text(2,20+(i+1)*15,""+i); } } private void ansichtCanvas(int kapazitaet) { initCanvas(kapazitaet); int[] zeileAlt = new int[kapazitaet+1]; int[] zeileNeu = new int[kapazitaet+1]; for(int z = 1; z <= gegenstaende.size();z++) { System.arraycopy(zeileNeu, 0, zeileAlt, 0, zeileNeu.length); int gewicht = (int)gegenstaende.get(z).getX(); for(int s = 0; s <= kapazitaet; s++) { if(s < gewicht) { zeileNeu[s] = zeileAlt[s]; canvas.setColor(255,0,0); canvas.text(30+s*25,5+(z+1)*15,""+zeileAlt[s]); canvas.setColor(0,0,0); canvas.text(30+s*25,20+(z+1)*15,""+zeileNeu[s]); canvas.text(30+s*25,5+(z+1)*15,""+zeileAlt[s]); } else { int temp = zeileAlt[s-gewicht] + (int)gegenstaende.get(z).getY(); if(temp>zeileAlt[s]) { zeileNeu[s] = temp; canvas.setColor(255,0,0); canvas.text(30+s*25,20+(z+1)*15,""+zeileNeu[s]); canvas.text(30+(s-gewicht)*25,5+(z+1)*15,""+zeileAlt[s-gewicht]); canvas.setColor(0,0,0); canvas.text(30+s*25,20+(z+1)*15,""+zeileNeu[s]); canvas.text(30+(s-gewicht)*25,5+(z+1)*15,""+zeileAlt[s-gewicht]); } else { zeileNeu[s] = zeileAlt[s]; canvas.setColor(255,0,0); canvas.text(30+s*25,5+(z+1)*15,""+zeileAlt[s]); canvas.setColor(0,0,0); canvas.text(30+s*25,20+(z+1)*15,""+zeileNeu[s]); canvas.text(30+s*25,5+(z+1)*15,""+zeileAlt[s]); } } } } }

Die folgende Canvas soll noch einmal die iterative Abarbeitung grafisch veranschaulichen. Man erkennt sehr gut, wie die Berechnung zeilenweise passiert und immer die vorhergehende Zeile nur Berechnung der neuen mit einbezieht. Dies ist durch das Einfärben der benutzten Werte kenntlich gemacht (leider etwas schwer ersichtlich). Das Ergebnis steht dann wie formal schon bekannt ganz unten rechts in der Tabelle. Auch in der Grafik ist dies der Fall.

Aufgrund von verschiedenen Desktopauflösungen haben wir uns auf 1024 x egal entschieden und somit wird maximal eine Kapazität von 30 gezeichnet.

ansichtCanvas(30);

Aufwandsbetrachtung

Durch die iterative Abarbeitung kann man sehr schnell erkennen, dass sich der Aufwand aus der Anzahl der Zeilen und Spalten zusammensetzt. $\mathcal{O}(n*K) * \mathcal{O}(1) = \mathcal{O}(nK)$

Fasst man $K$ als Konstante auf, so erreicht man eine uniforme Komplexität, was einen linearen Aufwand von $\mathcal{O}(n)$ ergeben würde. Dies ist jedoch nicht der Fall, da aus praktischer Relevanz $n$ und $K$ zusammenhängen müssen und sich im Allgemeinen sogar ein exponentieller Aufwand ergibt.

Das ist darauf begründet, dass es sich bei dem Algorithmus zur Lösung des 0/1 Rucksackproblems um einen pseudopolynomialen Algorithmus handelt. Hier ist das uniforme Komplexitätsmaß nicht anwendbar, sondern wir benötigen zur Aufwandsbetrachtung die Bit-Komplexität, welche die Länge der Eingabewerte berücksichtigt.

Dazu müssen wir natürlich die Eingabelänge erst einmal feststellen. Dabei besteht die Eingabe aus $2n+1$ natürlichen Zahlen, nämlich sämtlichen Gewicht-Werte-Paaren $g_{1},g_{2},...,g_{n},w_{1},w_{2},...w_{n}$ und der Kapazität $K$ in Binärdarstellung. Auf dem Band einer Turingmaschine (dem dazugehörenden theoretischen Modell) kann dabei auf einem Feld nur ein Zeichen des Eingabealphabetes stehen, also genau ein Bit.

Nun definieren wir $\widehat{w} = max\{w_{1},w_{2},...,w_{n}\}$ und beschränken die Eingabelänge nach oben durch $\mathcal{O}(n*(log_{2}K+log_{2}\widehat{w})+log_{2}K) = \mathcal{O}(n*(log_{2}K+log_{2}\widehat{w}))$ . Lässt sich $K$ nun in der Form $K = 2^{n}$ darstellen und somit $\widehat{w} \leq 2^{n}$ , so erhalten wir für die Eingabelänge $\mathcal{O}(n^{2})$ und es ergibt sich eine exponentielle Rechenzeit des Algorithmus mit $\mathcal{O}(n * 2^{n})$ .

Polynomiale Rechenzeit lässt sich nur erreichen, wenn $K$ durch ein Polynom beschränkt wird, wie zum Beispiel $K \leq n^{10}$ , womit sich eine Rechenzeit in $\mathcal{O}(n^{11})$ ergibt. Das ist jedoch, wie eingangs bereits erwähnt, im Allgemeinen nicht der Fall. Darum spricht man von einem pseudopolynomialen Algorithmus.

Rekursive Berechnung

ohne memoizing

Zunächst wollen wir einen rekursiven Algorithmus ohne memoizing implementieren. Anhand der rekursiven Beschreibung bereitet uns das auch keine Schwierigkeiten und somit kommen wir zu folgender Funktion:

private int rekursiveAufrufe; private int gesamtwertRekursiv(int kapazitaet) { rekursiveAufrufe = 0; return gesamtWert(gegenstaende.size(),kapazitaet); } private int gesamtWert(int pos,int kapazitaet) { rekursiveAufrufe++; if(pos==0) { return 0; } else { if(gegenstaende.get(pos).getX()>kapazitaet) { return gesamtWert(pos-1,kapazitaet); } else { int var1 = gesamtWert(pos-1,kapazitaet); int var2 = gesamtWert(pos-1,kapazitaet-(int)gegenstaende.get(pos).getX()) + (int)gegenstaende.get(pos).getY(); return java.lang.Math.max(var1,var2); } } }

System.out.println("Ergebnis rekursiv ohne memoizing: " + gesamtwertRekursiv(120)); System.out.println("Rekursive Aufrufe: " + rekursiveAufrufe);

Wie man sehen kann, stimmt das Ergebnis mit dem der iterativen Lösung überein. Jedoch wurden offenbar einige Elemente mehrfach berechnet, da die Zahl der rekursiven Aufrufe deutlich größer ist, als die Anzahl aller Teilprobleme.

mit memoizing

Nun wollen wir den Algorithmus durch memoizing erweitern. Für die Tabelle verwenden wir in Java eine verschachtelte Hashmap der Form HashMap<Integer,HashMap<Integer,Integer>> um schnelle Zugriffe zu gewährleisten. Damit wird die Rechenzeit nicht wesentlich durch das Abfragen der Elemente beeinflusst.

private HashMap memoliste = new java.util.HashMap(); private int gesamtwertRekursivMemo(int kapazitaet) { rekursiveAufrufe = 0; return gesamtWert1(gegenstaende.size(),kapazitaet); } private int gesamtWert1(int pos,int kapazitaet) { rekursiveAufrufe++; if(pos==0) { return 0; } else { if(gegenstaende.get(pos).getX()>kapazitaet) { return gesamtWertMemo(pos-1,kapazitaet); } else { int var1 = gesamtWertMemo(pos-1,kapazitaet); int var2 = gesamtWertMemo(pos-1,kapazitaet-(int)gegenstaende.get(pos).getX()) + (int)gegenstaende.get(pos).getY(); return java.lang.Math.max(var1,var2); } } } private int gesamtWertMemo(int pos, int kapazitaet) { if(memoliste.containsKey(pos)) { if(memoliste.get(pos).containsKey(kapazitaet)) { return memoliste.get(pos).get(kapazitaet); } else { int resultat = gesamtWert1(pos,kapazitaet); memoliste.get(pos).put(kapazitaet, resultat); return resultat; } } else { int resultat = gesamtWert1(pos,kapazitaet); HashMap temp = new HashMap(); temp.put(kapazitaet, resultat); memoliste.put(pos, temp); return resultat; } } private int getLengthMemoListe() { int size = 0; for(int i= 0 ; i < memoliste.size();i++) { size+=memoliste.get(i).size(); } return size; }

System.out.println("Ergebnis rekursiv mit memoizing: " + gesamtwertRekursivMemo(120)); System.out.println("Rekursive Aufrufe: " + rekursiveAufrufe); System.out.println("Länge der Memoliste: " + getLengthMemoListe()); System.out.println("----------------------"); System.out.println("Ergebnis rekursiv mit memoizing: " + gesamtwertRekursivMemo(120)); System.out.println("Rekursive Aufrufe: " + rekursiveAufrufe); System.out.println("Länge der Memoliste: " + getLengthMemoListe());

Man kann erkennen, dass wir auch mit memoizing den selben Wert erhalten wie bereits zuvor. Jedoch ist die Zahl der rekursiven Aufrufe deutlich geringer als ohne memoizing und es werden sogar weniger Teilprobleme gelöst als bei der iterativen Variante. Dort mussten ja sämtliche Tabellenelemente, also insgesamt 1331 Teilprobleme berechnet werden. Außerdem sieht man, dass die Länge der memoliste mit der Anzahl der rekursiven Aufrufe nahezu übereinstimmt. Hinzu kommt, dass bei einem erneuten Aufruf, der Algorithmus aus der bereits gefüllten Memoliste einen Vorteil ziehen kann. Da unser Ergebnis ja bereits berechnet wurde, können wir einfach darauf zugreifen und benötigen somit nur einen rekursiven Aufruf, nämlich den ersten.

Fazit

Rekursive Berechnung mit memoizing ist also mindestens genauso schnell wie iterative Berechnung. Lediglich wenn alle Teilprobleme mindestens einmal berechnet werden müssen, ist die iterative Variante gewöhnlich um einen konstanten Faktor schneller wie die rekursive Variante. Dies spielt jedoch kaum eine Rolle, da man diese konstanten Faktoren bei der Aufwandsbetrachtung auch vernachlässigen kann. Zudem werden haufig nicht alle Teilprobleme benötigt und somit sollte die rekursive Variante, die nur die benötigten Teilprobleme berechnet, natürlich bevorzugt werden. Auch schon aus dem Grund, dass diese direkt aus der rekursiven Vorschrift abgeleitet werden kann. Dadurch wird eine fehleranfällige Transformation unnötig.

Optimale Teilstruktur

Möchte man ein Problem mithilfe dynamischer Programmierung lösen, wirft sich schnell eine entscheidende Frage auf: "Wie stelle ich die optimale Teilstruktur fest, bzw. existiert diese überhaupt?"

Wie wir uns erinnern, war dies ja die Vorraussetzung dafür, dass ein Problem überhaupt mit dynamischer Programmierung lösbar ist, da die Teilprobleme ihrerseits wieder eine optimale Lösung besitzen müssen. Wir müssen also absichern, dass der Bereich der von uns betrachteten Teilprobleme die von der optimalen Lösung verwendeten einschließt. Wir haben bereits beim Rucksackproblem die optimale Teilstruktur entdeckt, indem wir von der Annahme ausgegangen sind, dass ein optimal gepackter Rucksack aus einem bis dahin optimal gepacktem 'Teil-Rucksack' und einem weiteren hinzugefügten Gegenstand besteht. Diese Annahme lässt sich sehr leicht beweisen. Wenn der 'Teil-Rucksack' mit einer bestimmten 'Teil-Kapazität' vor dem Einpacken des nächsten Gegenstandes $G_{i}$ (der zur optimalen Lösung gehört) nämlich nicht optimal gepackt wäre, würde eine andere Lösung durch hinzufügen desselben Gegenstandes $G_{i}$ eine bessere Lösung ergeben als die optimale. Dies ist ganz klar ein Widerspruch und somit ist unsere vorherige Annahme damit auch bewiesen.

Vorgehensweise beim Aufdecken

So wie beim Aufdecken der optimalen Teilstruktur beim Rucksackproblem, können wir auch bei anderen Problemen einem allgemeinem Muster folgen:

1. Zunächst gilt es zu zeigen, dass ein Problem gelöst wird, indem man eine Wahl trifft, wie das Finden des optimal gepackten 'Teil-Rucksacks' ("Gegenstand dazupacken oder die anderen alle drin lassen?"). Nach Treffen dieser Wahl erhält man wiederum eines oder mehrere noch zu lösende Teilprobleme.

2. Weiterhin ist anzunehmen, dass die Wahl, die zu einer optimalen Lösung führt, zu einem gegebenen Problem bekannt ist. Wie diese Wahl getroffen wird, muss noch nicht bekannt sein.

3. Daraufhin ist nun zu bestimmen, welche Teilprobleme sich ergeben, wobei der resultierende Raum der Teilprobleme am bestmöglichsten beschrieben werden muss und möglichst klein sein sollte.

4. Nun ist noch zu zeigen, dass die Teilprobleme, die innerhalb einer optimalen Lösung verwendet werden, selbst optimal sein müssen. Dazu greift man auf ein "Cut & Paste-Verfahren" zurück, bei dem man annimmt, dass keine der Lösungen eines Teilproblems optimal ist und diese Annahme dann zum Widerspruch führt. Um das zu erreichen wird gezeigt, dass man eine bessere Lösung erhalten würde, wenn man die nicht optimale Lösung ausschneidet und eine optimale dafür einfügt.

Raum der Teilprobleme charakterisieren

Wie gesagt ist es bei der Charakterisierung des Raumes der Teilprobleme vorteilhaft, diesen zunächst so klein wie möglich zu halten. Später kann man diesen auch noch erweitern, falls dies notwendig ist.

Beim Rucksackproblem bestand der Raum der Teilprobleme aus optimal gepackten 'Teil-Rucksäcken' die eine geringere Kapazität besaßen, als der für die Gesamtlösung betrachtete Rucksack. Da diese Lösung gut funktionierte bestand keine Notwendigkeit den Raum der Teilprobleme weiter zu verallgemeinern.

Wie man an späteren Beispielen aber noch sehen wird, ist es nicht immer so leicht eine optimale Teilstruktur festzulegen. Diese variiert in den verschiedenen Problemgebieten zum Einen in der Anzahl der Teilprobleme die innerhalb der optimalen Lösung des Ausgangsproblems verwendet werden, zum Anderen aber auch in der Zahl der Auswahlmöglichkeiten bei der Entscheidung, welche Teilprobleme in einer optimalen Lösung verwendet werden. Dabei wird der Aufwand zur Lösung eines Problems, durch die Multiplikation dieser beiden Faktoren ermittelt.

Betrachten wir dazu noch einmal das Rucksackproblem, erkennen wir, dass sich dadurch unsere Aufwandsbetrachtung der Iterativen Berechnung bestätigt. Dabei entspricht die Kapazität $K$ des Rucksacks der Anzahl der Teilprobleme und die Anzahl der Gegenstände $n$ den Auswahlmöglichkeiten, die beim befüllen eines Rucksackes mit einer bestimmten Kapazität zu treffen sind. Das führt uns wie bereits bekannt zu einem Aufwand von $\mathcal{O}(Kn)$ . Dabei ist zu berücksichtigen, dass sich der Aufwand durch rekursive Berechnung mit memoizing im Allgemeinen verringert, da nur die Teilprobleme berechnet werden, die auch wirklich zur Lösung benötigt werden und Mehrfachberechnungen entfallen.

Ungewichteter einfacher Pfad

Das nachfolgende Beispiel zum ungewichteten, einfachen Pfad, soll verdeutlichen, dass es nicht vorteilhaft ist eine optimale Teilstruktur anzunehmen, wenn diese nicht vorhanden ist. Dabei betrachten wir das Problem des ungewichteten, kürzesten Pfades und das des ungewichteten, längsten, einfachen Pfades. Bei beiden ist ein gerichteter Graph $G = (V,E)$ und Knoten $u,v \in V$ gegeben.

Bei dem Problem des ungewichteten, kürzesten Pfades suchen wir einen Pfad von $u$ nach $v$ mit der minimalen Anzahl von Kanten. Dabei können wir auch $u \neq v$ vorraussetzen. Weiterhin muss jeder Pfad $p$ von $u$ nach $v$ auch einen dazwischenliegenden Knoten $w$ enthalten, der selbstverständlich auch $u$ oder $v$ sein kann. Mit dieser Feststellung können wir den Pfad $p = u \leadsto v$ in die Teilpfade $p_{1} = u \leadsto w$ und $p_{2} = w \leadsto v$ zerlegen. Dabei muss die Summe der Anzahl der Kanten in $p_{1}$ und $p_{2}$ gleich der Anzahl der Kanten in $p$ sein. Nun nehmen wir an, dass wenn $p$ ein optimaler Pfad von $u$ nach $v$ ist, dann ist $p_{1}$ auch ein optimaler Pfad von $u$ nach $w$ . Dies lässt sich wiederum sehr einfach mit der 'Cut & Paste - Methode' beweisen. Das heißt wenn wir $p_{1}$ ausschneiden und einen anderen Pfad $p_{1}'$ dafür einfügen könnten, um einen Pfad $p'$ mit weniger Kanten als $p$ zu erhalten, würde dass der optimalen Eigenschaft von $p$ wiedersprechen. Dasselbe gilt natürlich analog für $p_{2}$ .

Im konkreten Beispiel kann man natürlich am besten erkennen, dass ein optimaler Pfad $p$ von $a$ nach $d$ in $G$ aus den Teilpfaden $p_{1} = a \rightarrow b$ und $p_{2} = b \rightarrow d$ besteht und dass diese ebenfalls optimal sein müssen.

Betrachten wir nun das Problem des ungewichteten, längsten, einfachen Pfades. Was beim Problem des kürzesten Pfades fast offensichtlich ist, nämlich, dass es sich um einfache Pfade handeln muss, da jeder Zyklus nicht zu einer optimalen Lösung gehören kann; muss hier als zusätzliche Einschränkung dienen, da der längste Pfad sonst unendlich viele Zyklen enthalten würde. Natürlich ist es verlockend anzunehmen, dass dieses Problem ebenfalls optimale Teilstruktur aufweist. Dies ist jedoch gerade nicht der Fall. Unterteilt man den Pfad $p = u \leadsto v$ Analog zum vorhergehenden Problem in die Teilprobleme $p_{1} = u \leadsto w$ und $p_{2} = w \leadsto v$ , so muss man feststellen, dass die Teilprobleme ihrerseits nicht optimal sind.

Als Beispiel betrachten wir wieder den Pfad von $a$ nach $d$ in $G$ . Man kann erkennen, dass ein längster, einfacher Pfad $p = a \leadsto d$ , unterteilt werden kann in die Teilprobleme $p_{1} = a \rightarrow b$ und $p_{2} = b \rightarrow d$ . Dabei sind die Teilprobleme jedoch keinesfalls optimal, da der längste, einfache Pfad von $a$ nach $b$ nicht $a \rightarrow b$ ist, sondern $a \rightarrow c \rightarrow d \rightarrow b$ . Tatsächlich lässt sich für dieses Problem auch keine optimale Teilstruktur finden. Somit wurde gezeigt, dass es besser ist keine optimale Teilstruktur anzunehmen, wenn diese nicht vorhanden ist.

Beispiele

Fibonacci-Zahl

ohne memoizing

int fib(int n) { if (n < 2) { return 1; } else { return fib(n - 1) + fib(n - 2); } }

System.out.println(fib(15));

mit memoizing

private java.util.HashMap fibs = new java.util.HashMap(); fibs.put(0, java.math.BigInteger.ONE); fibs.put(1, java.math.BigInteger.ONE); private java.math.BigInteger fib_mem(Integer n) { if(fibs.containsKey(n)) { return fibs.get(n); } else { java.math.BigInteger fib1 = fib_mem(n - 1); fibs.put(n-1, fib1); java.math.BigInteger fib2 = fib_mem(n - 2); return (fib1.add(fib2)); } }

System.out.println(fib_mem(30));

Rundreiseproblem

Optimalitätsbedingung

Auch für das Rundreiseproblem lässt sich sehr schnell eine Lösung mit Hilfe dynamischer Programmierung finden. Dabei wollen wir zunächst die Optimalitätsbedingung prüfen.

Wir stellen fest, dass eine Rundreise die in der Stadt $i = 1$ beginnt, alle anderen Städte genau einmal besucht und dann wieder in $1$ endet, unterteilt werden kann in den direkten Weg von $i = 1$ nach einer Stadt $j$ und der weiteren Rundreise durch alle Städte aus $S = \{2,3,\cdots ,n\}\backslash \{j\}$ die wieder in $1$ endet. Dabei ist anzunehmen, dass bei einer optimalen Gesamtlösung, der Weg von $j$ nach $1$ wieder optimal sein muss. Das lässt sich wieder sehr einfach mit dem bereits bekannten Widerspruchsbeweis bestätigen.

Rekursive Beschreibung der Lösung

Mit unseren Überlegungen erhalten wir somit schnell eine rekursive Beschreibung des minimalen Gesamtwegs $weg(1,\{2,3,4,\cdots ,n\})$ :

Sind alle Städte besucht, geht man von der aktuellen Stadt $i$ zurück nach $1$ , sonst suchen wir den kürzesten verbleibenden Rundweg.

Oder in mathematischer Notation: $weg(i,S) = \begin{cases} e_{i,1}, & wenn \ S = \emptyset \\ \min\limits_{j\in S}(e_{i,j} + weg(j,S\backslash \{j\})), & sonst \end{cases}$

Aufwandsbetrachtung

Die Tabelle zum speichern der Zwischenlösungen, die beim iterativen Vorgehen entsteht, besitzt die Dimensionen $n$ Spalten ( $2,3,4,\cdots ,n,1$ ) für die Städte und $2^{n-1}$ Zeilen für alle möglichen Städtemengen (also die Potenzmenge $\wp(\{2,3,4,\cdots ,n\})$ ). Bei der Minimumbildung ist die Anzahl der Summen wiederum durch $j$ bestimmt und benötigt somit einen Aufwand von $\mathcal{O}(n)$ .

Somit ergibt sich mit der Anzahl der Tabellenfelder $n\cdot 2^{n-1}$ ein Aufwand von $\mathcal{O}(n^22^n)$ .

Implementierung

Als Beispiel verwenden wir die Entfernungsmatrix E2 aus Verzweigen und Beschränken (siehe Abschnitt 6.3 im Buch [ $\downarrow$ Ch. Wagenknecht: Algorithmen und Komplexität]).

$\begin{array}{c|c|c|c|c} & \multicolumn{4}{c}{\text{nach}} \\ \text{von} & \text{1} & \text{2} & \text{3} & \text{4} \\ \hline \text{1} & \infty & 20 & 15 & 10 \\ \text{2} & 8 & \infty & 9 & 8 \\ \text{3} & 6 & 12 & \infty & 13 \\ \text{4} & 5 & 10 & 9 & \infty \end{array}$

int[][] e2 = new int[4][]; e2[0] = new int[]{Integer.MAX_VALUE,20,15,10}; e2[1] = new int[]{8,Integer.MAX_VALUE,9,8}; e2[2] = new int[]{6,12,Integer.MAX_VALUE,13}; e2[3] = new int[]{5,10,9,Integer.MAX_VALUE};

Die rekursive Implementierung mit Java fällt nun nicht sonderlich schwer, da sie sich direkt aus der rekursiven Vorschrift ableiten lässt.

//Liste aller Städte außer der ersten mit Index 0 java.util.LinkedList s = new java.util.LinkedList(); s.add(1); s.add(2); s.add(3); private int weg(int i,java.util.LinkedList s) { if(s.isEmpty()) { return e2[i][0]; } else { int back = Integer.MAX_VALUE; for(int z = 0; z < s.size() ; z++) { int j = s.get(z); //klonen der Liste, da bei jedem Schleifendurchlauf sonst die Liste immer kleiner wird java.util.LinkedList l = (java.util.LinkedList)s.clone(); l.remove(z); int temp = e2[i][j] + weg(j,l); back = java.lang.Math.min(back,temp); } return back; } }

weg(0,s);

Der obige Aufruf der Prozedur mit den Parametern $0$ (die erste Stadt) und $s$ (die Liste der anderen Städte) liefert uns das erwartete Ergebnis $35$ .

Aufgaben

Die Lösungen zu den Aufgaben sind teilweise schon im Wiki enthalten, wurden teilweise in der Vorlesung erzählt und/oder sind als Download bei den Files zu erhalten.

Desweiteren können die Aufgaben auch live im Wiki bearbeitet werden, dabei werden die Lösungen für den eingeloggten Benutzer gespeichert (nach dem Klick auf Ausführen).

Dabei ist es empfehlenswert, die Aufgaben zunächst lokal mit Hilfe einer IDE wie Netbeans oder Eclipse zu testen, bevor man diese ins Wiki übernimmt. Es kann auch vorkommen, dass gerade bei den Fibonacci-Zahlen in bestimmten Browsern Probleme auftreten, da nicht genug Speicher für die Java-Umgebung bereitgestellt wird. In diesem Fall sollten die Aufgaben auch lieber lokal getestet werden.

Fibonacci

Implementieren Sie verschiedene Versionen von der Fibonacci-Funktion.

$fib(n) = \begin{cases} 1, & wenn \ n < 2 \\ fib(n-1)+fib(n-2),& sonst \\ \end{cases}$

Mithilfe dieser Funktion kann man sehr schnell erkennen wie dynamische Programmierung/Optimierung funktioniert und auch welchen Gewinn man davon hat.

ohne Memo rekursiv

Implementieren Sie diese Funktion anhand der oben gegeben mathematischen Gleichung ohne Memoizing.

int myFib(int n) { // Fib berechnen return 0; }

Quelltext überprüfen:

System.out.println(myFib(11));

mit Memo rekursiv

Die 'Standart-Funktion' wird je nach Rechnenleistung bei fib(>70) praktisch unlösbar.

Deswegen sollen Sie nun die Funktion so erweiteren, das man noch fib von 200 berechnen kann. Als kleiner Tipp, nutzen Sie Memoizing und sein sie sich gegenüber ehrlich und probieren es erst, bevor Sie nach schauen. ;)

Da bei der Berechnung großer Fibonacci-Zahlen extrem große Werte entstehen, verwenden wir hier die Java Klasse java.math.BigInteger, die nach oben nicht beschränkt ist (maximal durch den Speicher), was die Größe der Zahlen betrifft. Deshalb ist es sinnvoll sich zunächst, zumindest mit den grundlegenden Operationen dieser Klasse vertraut zu machen. Dazu wird die Java-API empfohlen, zu finden unter: API:BigInteger. Zudem kann es vorteilhaft sein, sich noch einmal mit den Methoden der java.util.HashMap vertraut zu machen, damit die Methodennamen keine Schwierigkeiten bereiten. Die API dazu findet ihr hier: API:HashMap.

java.util.HashMap myFibs = new java.util.HashMap(); java.math.BigInteger myFibMemo(int n) { // Fib mit Memo berechnen return new java.math.BigInteger("0"); }

Quelltext überprüfen:

System.out.println(myFibMemo(251));

Iterative Lösung von Fib

Wir haben bis jetzt schon viel über Fibonacci geredet, jedoch immer nur über die rekursive Lösung. Warum nicht einmal Iterativ lösen?

Deswegen mal die Aufgabe zur Iterativen Lösung von Fib.

Was können Sie über das Speicherverhalten, Stackverhalten und auch den Aufwand sagen?

java.math.BigInteger myFibIterativ(int n) { // Fib Iterativ lösen return new java.math.BigInteger("0"); }

Quelltext überprüfen:

System.out.println(myFibIterativ(251));

Zusatz: mit Memo und fast konstantem Speicheraufwand

Optimieren Sie nun die vorhergehende Version so, das nun auch noch Fib von 5000 berechnet werden kann. Sollten Sie dieses Problem schnell behoben haben, bauen Sie diese Funktion noch so um, dass nun auch fib von 50000 berechnet werden kann.

Warum tritt in Java der StackOverflowError auf?

Was können Sie über das Speicherverhalten von Fib sagen?

Diese Aufgaben könnte man in kleinen Diskussionsrunden klären.

java.util.HashMap myFibsOpt = new java.util.HashMap(); java.math.BigInteger myFibMemoOpt(int n) { // Optimierte Fib mit Memo berechnen // Fib mit Memo berechnen return new java.math.BigInteger("0"); }

Quelltext überprüfen:

System.out.println(myFibMemoOpt(10000));

Matritzen-Kettenmultiplikation

Schreiben Sie eine Funktion, die die optimale Klammerung der Matritzen-Kettenmultiplikation vornimmt, mit dem Ziel, dass die geringsten Operationen bei der Multiplikation entstehen. Sie können dazu die unten angegeben Methode verwenden zum erzeugen von Matrizen mit Zufallswerten.

Beispiel: der Aufruf generateMatrix(4, 5, 10); liefert eine Matrix mit 4 Zeilen, 5 Spalten und Werten zwischen 0 und 9, repräsentiert als int[zeilen][spalten].

private void printMatrix(int[][] mat) { for(int i = 0; i < mat.length;i++) { String out = "("; for(int j = 0; j < mat[0].length;j++) { out+=mat[i][j]+" "; } System.out.println(out+")"); } }

private int[][] generateMatrix(int rows, int columns, int numbersize) { java.util.Random random = new java.util.Random(); int[][] back = new int[rows][columns]; for(int i = 0 ; i < rows ; i++) { for(int j = 0; j < columns ; j++) { back[i][j] = random.nextInt(numbersize); } } return back; }

printMatrix(generateMatrix(4,5,10));

Als Hilfestellung sind die Liste zum speichern der Matrizen und die Memoliste schon vorgegeben. Diese ist vom Typ HashMap<Integer,HashMap<Integer,Integer>>. Ebenso kann man die HashMap kListe verwenden zum speichern der Position, an der die Kette bei einer optimalen Klammerung aufgespalten wird.

Hier nochmal die rekursive Formulierung des Algorithmus in mathematischer Notation:

$m[i,j] = \begin{cases} 0, & falls \ i = j \\ \min\limits_{i\leq k<j} \{ m[i,j] = m[i,k] + m[k+1,j]+p_{i-1}\cdot p_k\cdot p_j \}, & falls \ i<j \end{cases}$

private java.util.List matrizen = new java.util.LinkedList(); private java.util.HashMap memoListe = new java.util.HashMap(); private java.util.HashMap kListe = new java.util.HashMap(); matrizen.add(generateMatrix(4,5,10)); matrizen.add(generateMatrix(5,2,10)); matrizen.add(generateMatrix(2,7,10)); matrizen.add(generateMatrix(7,3,10)); matrizen.add(generateMatrix(3,9,10)); //hier können weitere Matrizen hinzugefügt werden //dabei bitte auf Kompatibilität achten for(int i = 0; i < matrizen.size(); i++) { memoListe.put(i, new HashMap()); kListe.put(i, new HashMap()); for(int j = 0; j < matrizen.size();j++) { memoListe.get(i).put(j, Integer.MAX_VALUE); //initialisieren der MemoListe mit sehr großen Werten } } private int minMult(int i,int j) { return 0; }

private int minMult1(int i,int j) { if(memoListe.get(i).get(j)<Integer.MAX_VALUE) { return memoListe.get(i).get(j); } rekursiveAufrufe++; if(i==j) { return 0; } else { int back = Integer.MAX_VALUE; for(int k = i ; k < j ; k++) { int temp = minMult1(i,k) + minMult1(k+1,j) + (matrizen.get(i).length * matrizen.get(j)[0].length * matrizen.get(k)[0].length); back = java.lang.Math.min(back, temp); if(back<memoListe.get(i).get(j)) { memoListe.get(i).remove(j); memoListe.get(i).put(j, back); kListe.get(i).put(j, k); } } return back; } }

Quelltext überprüfen:

minMult(0,matrizen.size()-1);

Versuchen Sie auch die optimale Klammerung für eine Kette $(4\times 5),(5\times 2),(2\times 7),(7\times 3)$ per Hand mithilfe der naiven Methode zu finden.

Sie werden feststellen, dass es bereits bei 4 Matrizen schon einen erheblichen Aufwand bedeutet.

Zusatz: Ausgabe der optimalen Klammerung

Verwenden Sie die kListe und schreiben sie eine Methode, die die optimale Klammerung ausgibt.

private String optimaleKlammerung(int i,int j)//Ausgabe der optimalen Klammerung als String { return ""; }

minMult(0,matrizen.size()-1); System.out.println(optimaleKlammerung(0,matrizen.size()-1));

Beispiele aus der Vorlesung

Desweiteren können Sie gerne die Aufgaben aus der Vorlesung noch lösen, auch dazu können Sie uns fragen.

Hilfe?

Fragen Sie einfach die Übungsleiter Ullrich oder Baum.

Files

Vortragsfolien

Vortrag-AuK.pdf (0.7 MB)

Lösungen zu den Aufgaben

DynProgrammierung_Loesung.zip (0.1 MB)

Lösungen im Wiki: Lösungen_Dynamisches_Programmieren

Links

MSDN F#

F# Compiler Download (auch für Mono)

Einführung F#

Literatur

Th. H. Cormen, Ch. E. Leiserson, R. Rivest, C. Stein: Algorithmen - Eine Einführung, 2.Auflage, Oldenbourg Wissenschaftsverlag GmbH 2007, ISBN 978-3-486-58262-8

Gessner, Wacker: Dynamische Optimierung - Einführung-Modelle-Computerprogramme, 1.Auflage, Carl Hanser Verlag 1972, ISBN 3-446-11539-0

Ch. Wagenknecht: Algorithmen und Komplexität, 1.Auflage, Carl Hanser Verlag 2003, ISBN 3-446-22314-2

A. Iwainsky: Dynamische Optimierung - Gegenstand-Methoden-Möglichkeiten, 1.Auflage, VEB Verlag Technik Berlin 1984

J. Hinrichsen: Branch- and Bound-Verfahren zur Lösung des Rundreiseproblems, Vandenhoeck & Ruprecht Göttingen 1975, ISBN 3-525-12432-5

S. Wolfgang, U. Gerhard: Dissertation Duale Entartung in der lineare Optimierung, Transportproblem mit zusätzlichen Nebenbedingungen und Rundreiseproblem TU Dresden und Bergakademie Freiberg, 21.02.1975

Dynamisches Programmieren SS09

Aus ProgrammingWiki

Inhaltsverzeichnis

Eigenschaften

Bottom-up

Schwierigkeiten

Überlappende Teilprobleme

Iterativ oder rekursiv?

Iterative Berechnung

Rückkehr des Rucksackproblems

Dimension der Tabelle

Implementation

Aufwandsbetrachtung

Rekursive Berechnung

ohne memoizing

mit memoizing

Fazit

Optimale Teilstruktur

Vorgehensweise beim Aufdecken

Raum der Teilprobleme charakterisieren

Ungewichteter einfacher Pfad

Beispiele

Fibonacci-Zahl

ohne memoizing

mit memoizing

Rundreiseproblem

Optimalitätsbedingung

Rekursive Beschreibung der Lösung

Aufwandsbetrachtung

Implementierung

Aufgaben

Fibonacci

ohne Memo rekursiv

mit Memo rekursiv

Iterative Lösung von Fib

Zusatz: mit Memo und fast konstantem Speicheraufwand

Matritzen-Kettenmultiplikation

Zusatz: Ausgabe der optimalen Klammerung

Beispiele aus der Vorlesung

Hilfe?

Files

Vortragsfolien

Lösungen zu den Aufgaben

Links

Literatur

Ansichten

Persönliche Werkzeuge

Navigation

Suche

Werkzeuge