Approximationsalgorithmen
Aus ProgrammingWiki
Bereits von probabilistischen Algorithmen ist bekannt, dass diese in manchen Fällen nicht die optimale Lösung bestimmen. Aber sie sind effizient und in vielen Fällen die einzige Möglichkeit praktisch überhaupt ein brauchbares Ergebnis zu erzielen. Ganz ähnlich verhält es sich mit Approximationsalgorithmen. Der Hauptunterschied besteht jedoch darin, dass nicht der Zufall allein bestimmt, wie gut das Ergebnis wird, sondern dass durch analytisches Vorgehen eine Lösung angenähert wird.
Eine Approximation verfolgt immer eine bestimmte Idee (eine Heuristik) von der man glaubt, dass sie (zumindest im Mittel) einen direkteren Weg hin zur Lösung bietet. Eine Approximation wird damit zu einer gezielten Suche, bei der jeder Schritt (direkt oder indirekt) etwas näher zum Ergebnis führt.
Inhaltsverzeichnis |
Lokale Suche
Eine sehr einfache Heuristik ist die ganz allgemeine Idee, von den momentan zur Verfügung stehenden Schritten, einfach den auszuwählen, der vermeintlich am ehesten zur Lösung führt. Die Lokalität der Suche bezieht sich hierbei nicht auf einen bestimmten Ort, sondern eine begrenzte Menge von momentan verfügbaren Informationen. Anhand dieser lokalen Informationen wird die Entscheidung getroffen, in welche Richtung weiter gesucht wird.
Hill Climbing
Der Name steht für das anschauliche Beispiel der Suche nach dem Gipfel eines Berges, wobei an jeder Kreuzung stets der Weg eingeschlagen wird, der am steilsten nach oben führt (Gradientenaufstieg). Ohne Zweifel wird man auf diesem Weg den nächstgelegenen Gipfel erreichen. Bei dieser sehr einfachen Art der lokalen Suche wird versucht, basierend auf der aktuellen Situation, diese zu verbessern. Dazu wird die aktuelle Lösung leicht verändert und untersucht, ob sich eine Verbesserung ergeben hat. Wenn dem so ist, wird eben diese Lösung zur aktuellen Lösung und weitere Veränderungen können folgen.
Wir betrachten als Beispiel das $n$-Damen-Problem, das nach konfliktfreien Aufstellungen von möglichst vielen Damen auf einem $n$x$n$-Schachbrett fragt. (Aufgrund der gegebenen Spielregeln ist sofort einzusehen, dass es höchstens $n$ Damen sein können.) Würde man dieses Problem systematisch mittels Backtracking (Tiefensuche) lösen, würde das einen exponentiellen Aufwand nach sich ziehen.
Die Hill-Climbing-Strategie beginnt mit einer beliebigen Anfangsaufstellung von Damen, die dann solange verändert wird, bis sich keine Verbesserung mehr ergibt. Um ein Verbesserung feststellen zu können, muss eine Bewertung der aktuellen Damen-Positionen vorgenommen werden. Dies kann sehr einfach bewerkstelligt werden, indem die Anzahl der Konflikte ermittelt wird, also die Anzahl der Möglichkeiten in denen sich zwei Damen wechselseitig bedrohen, d.h. schlagen, können.
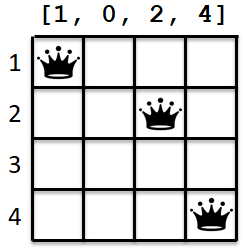
Im folgenden Programm wird eine Damenbelegung als Liste der Länge $n$ repräsentiert. Jedes Element der Liste steht für eine Linie (Spalte) des Schachbretts und kann die Werte $0$ bis $n$ annehmen. $0$ steht dafür, dass in der entsprechenden Linie gar keine Dame steht. Die übrigen Zahlen $1$ bis $n$ stehen für die Reihe (Zeile) in der die Dame steht.
In der folgenden Abb. sind drei Damen auf einem $4$x$4$-Schachbrett aufgestellt. Obwohl die sie sich zwar nicht bedrohen, stellt diese Aufstellung keine (exakte) Lösung dar, denn es können $4$ (allg. $n$) Damen konfliktfrei untergebracht werden.
Die Ergebnisse zeigen, dass auch für große Schachbretter ein Ergebnis in relativ kurzer Zeit erzielt wird. Es ist aber auch erkennbar, dass selbst bei kleinen Schachbrettern (z.B. $n=6$ und $n=8$) nicht immer die Lösung, sondern nur eine Näherung mit sehr wenigen Konflikten gefunden wird.
Hill Climbing ist in dieser Form ein deterministisches Verfahren und selbst bei mehrfacher Wiederholung ändern sich die Ergebnisse nicht. Die einzige Möglichkeit, das Ergebnis zu beeinflussen, besteht hier darin, die Ausgangssituation, also die initialen Damenpositionen, zu verändern. Allgemein gilt: Die Güte der Ergebnisse von Hill Climbing Algorithmen ist in hohem Maße davon abhängig, wie die Initialsituation beschaffen ist.
Plateau Search
Das Hill Climbing wird immer nur solange fortgesetzt, bis von der aktuellen Situation aus keine bessere Situation mehr erreicht werden kann. Eine solche Situation wird lokales Optimum genannt. Im Allgemeinen ist man aber am globalen Optimium interessiert. Ein erster Schritt um nicht bei einem lokalen Optimum stecken zu bleiben ist die Plateau-Suche. Hier werden nicht nur bessere Teillösungen weiterverfolgt, sondern auch die, die genauso gut sind. Eine einfache Ersetzung von < durch <= reicht allerdings nicht aus für eine stabile Plateau-Suche. Die 6-Damen Ausgangssituation [1,2,3,4,5,6] würde dann z.B. mit o.a. Programm zu einer Endlosschleife führen.
Das Problem ist, dass es bei der Plateau-Suche nun möglich ist, durch Veränderung der Damen-Positionen eine Situation herbeizuführen, die bereits in einem vorherigen Schritt Ausgangssituation war. Beim einfachen Hill Climbing sind solche Zyklen nicht möglich. Um diese zu vermeiden, dürfen bereits geprüfte Situationen nicht erneut geprüft werden. Eine Tabu-Liste ist erforderlich. So führt auch o.g. Damen-Situation zu einem Ergebnis und die Chance ein globales Optimum zu ermitteln, ist um einiges gestiegen.
Hinweis: Bei komplexeren Problemen, kann die Tabu-Liste sehr groß werden. Sie nimmt damit sehr viel Speicherplatz ein und die Bestimmung ob ein Element enthalten ist dauert zunehmend länger. Um das zu vermeiden, wird meist in regelmäßigen Abständen die Größe der Liste geprüft und bei Überschreiten eines Limits Elemente aus dieser entfernt. Am sinnvollsten ist die Entfernung genau der Elemente, die sich am längsten in der Liste befinden.
Threshold Accepting
Bei der Plateau-Suche werden alle Teillösungen weiterverfolgt, die mindestens genauso gut sind wie die vorherige. Durch Threshold Accepting wird die Menge der weiterzuverfolgenden Teillösungen noch einmal erweitert. Hier werden auch schlechtere Teillösungen weiterverfolgt, solange sie nicht viel schlechter sind als die vorherigen. Dieses viel schlechter muss natürlich im Einzelfall konkret definiert werden. Beim oben beschriebenen $n$-Damen-Problem könnte z.B. die Differenz zwischen den Anzahlen der Konflikte zweier Situationen herangezogen werden. Lösungen, die z.B. nur einen Konflikt mehr haben als die Ausgangssituation, dürften dann weiterverfolgt werden. Auch hier ist eine Tabu-Liste erforderlich, um Zyklen zu vermeiden. Für das $6$-Damen-Problem mit der Ausgangssituation [1,2,3,4,5,6] wird durch Akzeptieren von Kandidaten, die um einen Konflikt schlechter sind, nun eine Lösung gefunden.
Hinweis: In diesem Programm ist better nach einem Durchlauf nicht zwangsläufig eine Verbesserung gegenüber best da auch schlechtere Teillösungen akzeptabel sind. Im Folgedurchlauf ist best damit nicht unbedingt das beste bereits gefundene Ergebnis. Gibt es z.B. eine zeitliche Begrenzung, dann sollte man sich das wirklich beste gefundene Ergebnis an anderer Stelle merken, um bei Ablauf des Zeitlimits dieses liefern zu können.
Viele weitere Variationen sind ebenfalls denkbar. So könnte der nächste Nachbar zufällig gewählt werden (nicht wie hier der bestmögliche) oder bei der Überprüfung auf Verbesserung könnte mit dem bisher besten Ergebnis verglichen werden (nicht wie hier mit dem zuletzt gefundenen) oder der übergebene Schwellwert t könnte im Verlauf gesenkt werden.
Simulated Annealing
Bei dieser Variation der lokalen Suche wird das Zulassen einer zwischenzeitlichen Verschlechterung einer gewissen Wahrscheinlichkeit unterworfen. Eine Verschlechterung ist also im Verlauf der Suche nur mit einer immer niedriger werdenden Wahrscheinlichkeit wirklich akzeptabel. Dieses Niedrigerwerden (diese Verringerung) wird in der Literatur oft mit dem Abkühlen eines geschmolzenen Materials verglichen. Praktisch ist es nur die stetige Verringerung eines Faktors, der bei der Entscheidung über die Akzeptanz der Verschlechterung mit einbezogen wird. Die Größe dieses Faktors und die Art und Weise wie dieser verringert wird, ist vom Problem abhängig und muss immer individuell festgelegt werden.
Im folgenden Programm ist ersichtlich, dass die Laufzeit, neben dem vorzeitigen Abbruch, wenn die Lösung gefunden wurde, nur durch die Verringerung des Faktors temp bestimmt wird. Das ist äußerst praktisch, da die maximale Dauer auf diese Weise weitestgehend unabhängig von der Größe des Problems ist.
Sollte der Browser während der Ausführung ein langsames Script melden, wählen Sie die Option „Warten“.
Hinweis: Eine Tabu-Liste ist hier nicht erforderlich, da die weiter zu verfolgenden Kandidaten zufällig ausgewählt werden. Zyklen sind so zwar immer noch möglich, aber es gibt die Möglichkeit diese auch wieder zu verlassen. Wird der nächste Kandidat systematisch ausgewählt (so wie in den Beispielen zu Plateau-Search und Threshold Accepting), gibt es diese Möglichkeit nicht.
Evolutionäre Algorithmen
Diese Art von Algorithmen beruht auf dem Prinzip der natürlichen Evolution bzw. der Genetik (genetische Algorithmen). Es geht also darum, Dinge miteinander auf zufällige Art zu kreuzen, um so Änderungen hervorzurufen, die möglicherweise zu Verbesserungen führen. Durch geziehlte Kreuzung ("Züchtung") kann Einfluss auf die Ergebnisse der Evolution genommen werden. Anders als bei der lokalen Suche, wo immer ausgehend von einem Momentanzustand ein Folgezustand ermittelt wird, wird hier mit Populationen gearbeitet, also einer ganzen Menge von Momentan- und Folgezuständen.
Aufbauend auf einer Basispopulation (einer Menge von Initialzuständen) werden folgende Schritte immer wieder durchlaufen:
- Auswahl einer Teilmenge aus der Basispopulation (Selektion für Rekombination)
- Kreuzungen innerhalb dieser Teilmenge erweitern die Basispopulation (Rekombination)
- Entfernen einer Teilmenge aus der Basispopulation (Selektion für Aussortierung: Fitness-Funktion)
Beim $n$-Damen-Problem könnten diese Schritte z.B. ausgehend von einer Population von 20 zufällig generierter Damen-Situationen folgendermaßen modelliert werden.
- Auswahl der 3 Damen-Situationen mit der geringsten Anzahl von Konflikten
- 4-fache Kreuzung der 3 Situationen führt zu 12 neuen Situationen
- Entfernung der 12 Situationen mit der höchsten Anzahl von Konflikten
Nicht für jedes Problem sind genetische Algorithmen geeignet. Auch beim $n$-Damen-Problem ist es, vor allem bei größeren $n$, äußerst unwahrscheinlich durch Rekombination eine Lösung zu finden. Neben der hier verwendeten Permutations-Rekombination gibt es viele weitere Varianten z.B. k-point-crossover, um Probleminstanzen zu neuen Instanzen zu kombinieren. Meist wird in genetischen Algorithmen auch Mutation zugelassen. Bei dieser werden neben der Änderung durch zufällige Kreuzung noch weitere zufällige spontane Änderungen mit einer gewissen Wahrscheinlichkeit zugelassen. Generell zeigen evolutionäre Ansätze eine Vielzahl von Parametern mit denen die Vorgänge gesteuert werden können. Hier die passenden Parameterwerte für ein konkretes Problem zu ermitteln, stellt eine nicht zu unterschätzende Schwierigkeit dar.