Randomisierte Algorithmen
Aus ProgrammingWiki
Algorithmen, in denen der Zufall eine Rolle spielt, werden randomisiert, probabilistisch oder stochastisch genannt. Dem Einsteiger stellt sich dabei zunächst die Frage, wie der Zufall effektiv bei der Lösung eines Problems helfen kann. Der "Zufallsregen" zeigt das sehr eindrucksvoll.
Inhaltsverzeichnis |
Numerische probabilistische Simulation
Wir betrachten diese Klasse von Monte-Carlo-Verfahren am Beispiel der Bestimmung einer Näherung für $\pi$.
Die Kreiszahl $\pi$ ist eine mathematische Konstante und definiert das Verhältnis zwischen Umfang $u$ und Durchmesser $d$ eines Kreises.
$$ \pi = \frac{u}{d} $$
Die Fläche $A$ eines Kreises ist definiert durch
$$ A = \frac{\pi}{4} d^2 $$
wobei $d^2$ nichts anderes als die Fläche des den Kreis umgebenden Quadrats ist. Die Zahl $\pi$ kann also berechnet werden durch
$$ \pi = 4 \frac{A}{d^2} $$
wobei $\frac{A}{d^2}$ einfach das Verhältnis zwischen den Flächeninhalten von Kreis und Quadrat ist.
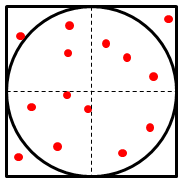
Zur Bestimmung dieses Verhältnisses kann man es nun zufällig Punkte (Koordinaten) auf das Quadrat (inkl. Kreis) regnen lassen. In Abb. 1 sind z.B. von den insgesamt 14 Tropfen zufällig 11 innerhalb des Kreises gelandet. Da die Flächen im Verhältnis $\frac{\pi}{4}$ stehen, müssen zufällig positionierte Koordinaten auch in eben diesem Verhältnis auf den Flächen verteilt sein. Für das Beispiel ergibt sich:
$$4\cdot\frac{\text{Anzahl der Tropfen im Kreis}}{\text{Anzahl der Tropfen im Quadrat}} = 4\cdot\frac{11}{14} = 3,142857143... \approx \pi = 3,141592654... $$
Mit einer größeren Anzahl von Zufallstropfen sollte sich dieses Verhältnis stabilisieren und eine bessere $\pi$-Näherung ergeben.
Implementation
Im Folgenden werden nur ein Viertel des Einheitskreises und dessen umgebendes Quadrat betrachtet. Da beide Flächen um den gleichen Prozentsatz verkleinert werden, hat das keinen Einfluss auf das Verhältnis der Flächen zueinander. Da für x und y nur Gleitkommazahlen im Intervall $[0,1]$ generiert werden, liegen alle Koordinaten innerhalb des Quadrats. Für jede Koordinate $(x,y)$ innerhalb des Kreises gilt $x^2+y^2 \leq 1$ . So kann sehr einfach ermittelt werden, ob sich ein zufälliger Tropfen innerhalb des Viertelkreises befindet.
Bei genauer Betrachtung wird man feststellen, dass dieses Programm auch für eine große Anzahl von Simulationen die $\pi$-Approximation nicht verbessern kann. Zum einen ist das darauf zurückzuführen, dass die Gleitkommazahlen mit denen hier gerechnet wird, nur eine begrenzte Genauigkeit aufweisen. Bei der Berechnung müssen intern also Rundungen durchgeführt werden, die zu einer Verfälschung des Ergebnisses führen. Zum anderen liegt die Ursache in der Berechnung der Zufallszahlen selbst.
Nicht-/Determinismus und Nicht-/Determiniertheit
Algorithmen, wie der "Zufallsregen", sind nichtdeterminiert, da sie bei gleichen Eingaben unterschiedliche Ergebnisse liefern können. Sie sind auch nichtdeterministisch.
Nichtdeterministische Algorithmen sind solche, die in jedem Schritt aus einem Zustand in genau einen aus mehreren möglichen Folgezuständen übergehen, s. NEA, NKA, NTM. Dies ist auch an verschiedenen möglichen Zwischenwerten erkennbar. Bei deterministischen Algorithmen gibt es nur jeweils genau einen bestimmten Folgezustand.
Zufallszahlengeneratoren, die im folgenden Abschnitt betrachtet werden, sind (überraschenderweise) determiniert und deterministisch.
Es gibt folgende Zusammenhänge zwischen Nicht-/Determinismus und Nicht-/Determiniertheit:
- Ein deterministischer Algorithmus ist stets determiniert. Die Umkehrung gilt nicht.
- Ein nichtdeterministischer Algorithmus kann sowohl determiniert als auch nichtdeterminiert sein.
Zufallszahlen
Das Ergebnis unter Einbeziehung des Zufallsregens beruht im wesentlichen darauf, dass die generierten Zufallszahlen auch wirklich zufällig sind. In korrekt arbeitenden Computersystemen gibt es aber generell keinen echten Zufall (eine Ausnahme bilden System die physikalische Werte messen). Zurecht darf also die Frage gestellt werden, was das Ergebnis des Aufrufs von > random() dann eigentlich ist.
Genau genommen sind diese Zahlen nämlich keine zufälligen Zahlen, denn sie werden durch einen deterministischen Algorithmus berechnet. Im Allgemeinen spricht man hier von Pseudozufallszahlen. Eine sehr einfacher Zufallszahlengenerator ist der lineare Kongruenzgenerator. Er wurde 1948 von Derrick Henry Lehmer entwickelt.
$$ z_n = (a \cdot z_{n-1}+b)\bmod c \text{ für } n\geq 1 $$
Die natürlichen Zahlen $a \in \{1,\dots, c-1\}$, $b \in \{0,\dots, c-1\}$ und $c \geq 2$ sind Konstanten, die die Güte des Generators beeinflussen. Die rekursive Notation weist darauf hin, dass die berechnete Zahl $z_n$ von der vorher berechneten Zahl $z_{n-1}$ abhängig ist. Ausgehend von einem beliebigen seed (Saat) $z_0 \in \mathbb{N}$ kann hier also eine Folge berechnet werden, deren einzelne Glieder bei geeigneter Konstantenwahl in der Tat zufällig aussehen.
Die Wahl der Konstanten $a$, $b$ und $c$ ist entscheidend für die Güte des Zufallsgenerators. Die Konstante $c$ gibt an wieviele verschiedene Zufallszahlen überhaupt möglich sind. Die möglichen Zufallszahlen sind $[0,c[$. Ein weiteres Gütemerkmal ist die Periodenlänge, also die Anzahl der Folgenglieder bis sich eine Zahl wiederholt. Diese kann maximiert werden indem ein $b$ gewählt wird, das zu $c$ teilerfremd ist, jeder Primfaktor von $c$ ein Teiler von $a-1$ ist und wenn $c$ durch 4 teilbar ist, auch $a-1$ durch 4 teilbar ist. Für die im Programmierbeispiel verwendeten Konstanten ist das der Fall.
Wiederholtes Ausführen mit gleichem $z_0$ wird stets die gleiche Folge von Zahlen generieren. Aus diesem Grund wird bei Zufallsgeneratoren in regelmäßigen Abständen oder auch manuell ein neues $z_o$ festgelegt. In Python gibt es dafür das Sprachelement random.seed(). Eine bewährte Praxis ist es, als seed (Startwert) die Systemzeit zu verwenden.
Las Vegas, Monte Carlo und Atlantic City
Die für das Glückspiel (der Zufall lässt grüßen) bekannten Städte sind Namensgeber für ein paar bestimmte Typen von probabilistischen Algorithmen.
Las Vegas Algorithmen liefern niemals falsche Ergebnisse und tun das mit einer gewissen Wahrscheinlichkeit auch schnell. Manchmal geraten sie allerdings in Sackgassen und liefern kein Resultat.
Im Gegenzug sind Monte Carlo Algorithmen immer schnell. Deren Ergebnisse sind aber möglicherweise falsch.
Atlantic City Algorithmen sind ein Kompromiss dieser beiden Typen. Sie sind fast immer schnell und liefern fast immer ein korrektes Ergebnis. Da der Entwurf von Atlantic City Algorithmen sehr schwierig ist, gibt es nur wenige.
Quicksort
Ein typisches Beispiel für einen Las Vegas Algorithmus erhält man durch Anpassung des Quicksort-Algorithmus. Normalerweise wird hier als Pivot-Element einfach das erste Element der zu sortierenden Liste verwendet. Ist die Liste aber bereits sortiert, führt dieses Verhalten zwangsläufig zur Worst-Case-Laufzeit von $\mathcal{O}(n^2)$, denn der Baum ist vollkommen schieflastig als Gegenteil zu balanciert. Im mittleren Fall wird $\mathcal{O}(n\log n)$ erzielt.
Wird das Pivot-Element dagegen zufällig ausgewählt, ändert sich etwas. Die Wahrscheinlichkeit ist gering, dass dabei immer das kleinste Element ausgewählt wird. In der Praxis kommen sortierte oder teilsortiere Listen öfter vor, sodass die o.g. Auswahlwahrscheinlichkeit gegenüber der Sortiertwahrscheinlichkeit eher gering ausfällt.
Somit ist das Las-Vegas-Quicksort mit einer hohen Wahrscheinlichkeit schneller als das Standard-Quicksort, d.h. im Allgemeinen wird sich $\mathcal{O}(n\log n)$ ergeben.
Das probabilistische Quicksort ist nichtdeterministisch aber determiniert, da es stets die gleiche sortierte Liste als Ergebnis liefert. Durch die freie Wahl des Trennelements entstehen verschiedene Zwischenwerte, die den jeweils ausgewählten Folgezustand ausmachen.
Äquivalenz zweier Multimengen
Wir betrachten Multimengen (Listen ohne Beachtung der Elementreihenfolge) $M_A$ und $M_B$, die $n$ natürliche Zahlen enthalten. Für zwei Multimengen kann man feststellen, ob sie äquivalent sind, d.h. genau die gleichen Elemente enthalten, indem diese zunächst sortiert und dann elementweise verglichen werden. Im Mittel benötigt eine solche Sortierung eine Laufzeit von $\mathcal{O}(n\log n)$. Für die vollständige Prüfung ergibt das im average case $\mathcal{O}(n+2n\log n)$: $\mathcal{O}(2n\log n)$ entfällt auf die Sortierung der beiden Multimengen und $\mathcal{O}(n)$ wird für die sich anschließende Zählschleife (zum elementweisen Vergleich) benötigt. Der Gesamtaufwand beträgt also $\mathcal{O}(n\log n)$.
Ein Monte Carlo Algorithmus kann das sehr viel effizienter, jedoch mit der Einschränkung, dass er sich manchmal irrt, d.h. das Ergebnis mit einer gewissen Wahrscheinlichkeit nicht stimmt.
Wir bilden für die beiden Multimengen $M_A=\{a_1,a_2,\ldots,a_n\}$ und $M_B=\{b_1,b_2,\ldots,b_n\}$ die folgenden Polynome:
$$ p_A(x) = (x-a_1)\cdot(x-a_2)\cdot\ldots\cdot(x-a_n) $$ $$ p_B(x) = (x-b_1)\cdot(x-b_2)\cdot\ldots\cdot(x-b_n) $$
Diese Darstellung ist für jede ganzrationale Zahl eindeutig. Die Multimengenelemente sind gerade die (evtl. mehrfachen) Nullstellen des jeweiligen Polynoms, sodass $p_A(x)=p_B(x)=0$ für $x=a_1,a_2,\ldots,a_n,b_1,b_2,\ldots,b_n$ gilt. Außerdem kann es Werte für $x$ geben, die die Forderung $p_A(x)=p_B(x)\neq 0$ erfüllen, obwohl die zugehörigen Multimengen nicht äquivalent sind.
$$ p_A(x) = (x-1)(x-2)(x-4)(x-5) $$ $$ p_B(x) = (x-7)(x-2)(x-4)(x-2) $$ $$ p_A(2) = 0 = p_B(2) $$ $$ p_A(3) = 4 = p_B(3) $$
Für die Prüfung auf Äquivalenz reichen einzelne $x$-Treffer also nicht aus. Es gilt
Satz:
$M_A\equiv M_B\text{ gdw. }p_A(x)=p_B(x)\text{ für alle } x\in\mathcal{N}$.
Auf dieser Basis soll nun ein MC-Algorithmus entworfen werden: Sobald für eines der zufällig gewählen $x$ gilt $p_A(x)\neq p_B(x)$, sind die beiden Multimengen mit Sicherheit nicht äquivalent. Anderenfalls sind sie vielleicht äquivalent.
Man kann aber die Treffsicherheit des Verfahrens erhöhen, indem der Algorithmus mit verschiedenen $x$ mehrfach ausgeführt wird. Es wird empfohlen mit relativ kleinem $|S|$, d.h. $x$ zufällig aus $S=\{1,2,3,\ldots,2n\}$, zu arbeiten und dafür die Zahl der Wiederholungen (etwas) zu vergrößern. In folgendem Beispiel reichen $5$ Wiederholungen aus, um festzustellen, dass die beiden Multimengen nicht äquivalent sind.
Damit arbeitet das Verfahren mit linearem Aufwand, d.h. in $\mathcal{O}(n)$, zum Preis, dass es sich manchmal irrt.
Das oben vorgestellte Verfahren wird beispielsweise in der Kriminalistik zum Vergleich von Fingerabdrücken angewandt.
FERMAT-scher Primzahltest
Auf der Basis des "kleinen Satzes von FERMAT" lässt sich ein sehr praktikables Monte-Carlo-Verfahren (kurz: MC-Verfahren) zur Primzahlbestimmung entwickeln.
Satz (FERMAT):
Für jede Primzahl $p$ und jede natürliche Zahl $a$ mit $1<a<p$ ist die Kongruenz $a^{p-1}\equiv 1\bmod p$ erfüllt.
Beweis:
als ÜA
Satz in Wenn-Dann-Form
Wenn $n$ eine Primzahl ist, dann gilt $a^{n-1}\equiv 1\bmod n$ für jede natürliche Zahl $a$ mit $1<a<n$.
In der Wenn-Dann-Form kann man die Implikation gut erkennen. Eine Äquivalenz (gdw) ist es nicht. Das bedeutet, dass es natürliche Zahlen geben kann, die den sog. FERMAT-Test bestehen und trotzdem keine Primzahlen sind. Man nennt sie Carmichael Zahlen. Bis $10000$ gibt es nur sieben solcher "Pseudoprimzahlen": $561, 1105, 1729, 2465, 2821, 6601, 8911$.
Wir arbeiten nun mit dem obigen Satz in Wenn-Dann-Form weiter und wenden prädikatenlogische Umformungsregeln an:
$$ A\rightarrow B \Leftrightarrow \lnot B\rightarrow \lnot A $$ $$ \lnot(\forall x: C(x)) \Leftrightarrow \exists x: \lnot C(x) $$
Satz:
Wenn es (mind.) eine natürliche Zahl $a$ mit $1<a<n$ gibt, die $a^{n-1}\not\equiv 1\bmod n$ erfüllt, dann ist $n$ eine zusammengesetzte Zahl (keine Primzahl).
Bemerkung: Definitionsgemäß sind $a$ mit $1<a<n$ und $n$ teilerfremd, wenn $n$ eine Primzahl ist. Primzahlen haben keine Teiler außer sich selbst und $1$.
Beweis:
Aus dem kleinen Satz von FERMAT unter Anwendung der o.g. Umformungsregeln aus der Prädikatenlogik:
$A$: $n$ ist Primzahl
$B$: jede natürliche Zahl $a$ mit $1<a<p$ erfüllt $a^{n-1}\equiv 1\bmod n$
$\lnot A$: $n$ ist keine Primzahl
$\lnot B$: Es gibt eine natürliche Zahl $a$ mit $1<a<n$, die $a^{n-1}\equiv 1\bmod n$ nicht erfüllt.
Wir können nun einen MC-Algorithmus für die Primzahlbestimmung formulieren. Die Eingaben sind $n$ und eine Anzahl von Wiederholungen, die die Treffsicherheit des MC-Algorithmus' erhöhen sollen.
- Wenn $n=2$, dann handelt es sich lt. Def. um eine Primzahl, d.h. das Ergebnis ist True.
- Wenn $n$ gerade, ist $n$ keine Primzahl, d.h. das Ergebnis lautet False.
- Wähle (zufällig) ein $a$ mit $1<a<n$.
Wenn dieses $a$ und $n$ nicht teilerfremd sind,
dann kann $n$ keine Primzahl sein und das Ergebnis heißt False,
sonst wenn $a^{n-1}\not\equiv 1\bmod n$, dann heißt das Ergebnis False.
Schritt 3 mehrfach ausführen! - Das Ergebnis heißt (vermutlich) True.
Schon $8$ Wiederholungen reichen aus, damit sich dieses Programm für die Carmichael-Zahl $8911$ fast nicht irrt und (meist) das korrekte Ergebnis, nämlich >False, berechnet.
Primzahltest von Solovay und Strassen
Ein weiteres MC-Verfahren zum Test von Primzahlen beruht ebenfalls auf dem kleinen Satz von FERMAT und verwendet das Jacobi-Symbol (aus der Zahlentheorie).
Satz:
Wenn $n$ eine Primzahl ist, dann gilt für alle natürlichen Zahlen $a$ mit $1<a<n$ und $ggt(a,n)=1$ die Kongruenz $\mathcal{J}(a,n)\equiv a^\frac{n-1}{2}\bmod n$.
$\mathcal{J}(a,n)$ kann nur die Werte $+1$ und $-1$ annehmen.
15 is composite 13 is prime
Den oben angegebenen Code kann man verkürzen, wenn man die in sympy definierte jacobi_symbol-Funktion verwendet.
-1 1
Monte-Carlo-Algorithmen sind also nichtdeterministisch und nichtdeterminiert.