Vorlesung 1 Lemke

Aus ProgrammingWiki

Inhaltsverzeichnis 1 Beweis Widerlegungsgesetz 2 Indirekter Beweis S. 27 3 Beispiel vollständige Induktion - nachgerechnet 4 Übungsaufgaben zur vollständigen Induktion 5 Interpreter für aussagenlogische Ausdrücke (FLACI) 6 Partielle Funktionen - Programmatisch umgesetztes Beispiel 7 Selbstgewähltes Beispiel für eine partielle Funktion 8 Injektiv, Surjektiv, Bijektiv 9 Injektiv 10 Surjektiv 11 Bijektiv 12 Injektiv und surjektiv 13 Injektiv, nicht surjektiv 14 Surjektiv, nicht injektiv 15 Weder surjektiv, noch injektiv

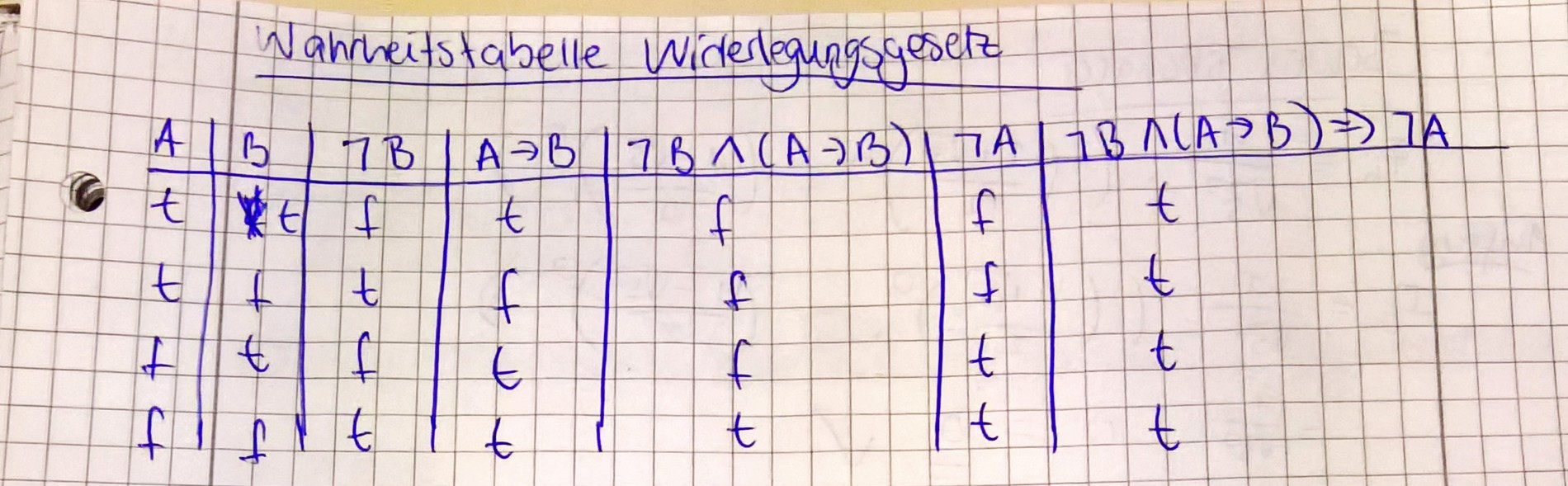
Beweis Widerlegungsgesetz

.

Indirekter Beweis S. 27

Beispiel vollständige Induktion - nachgerechnet

Übungsaufgaben zur vollständigen Induktion

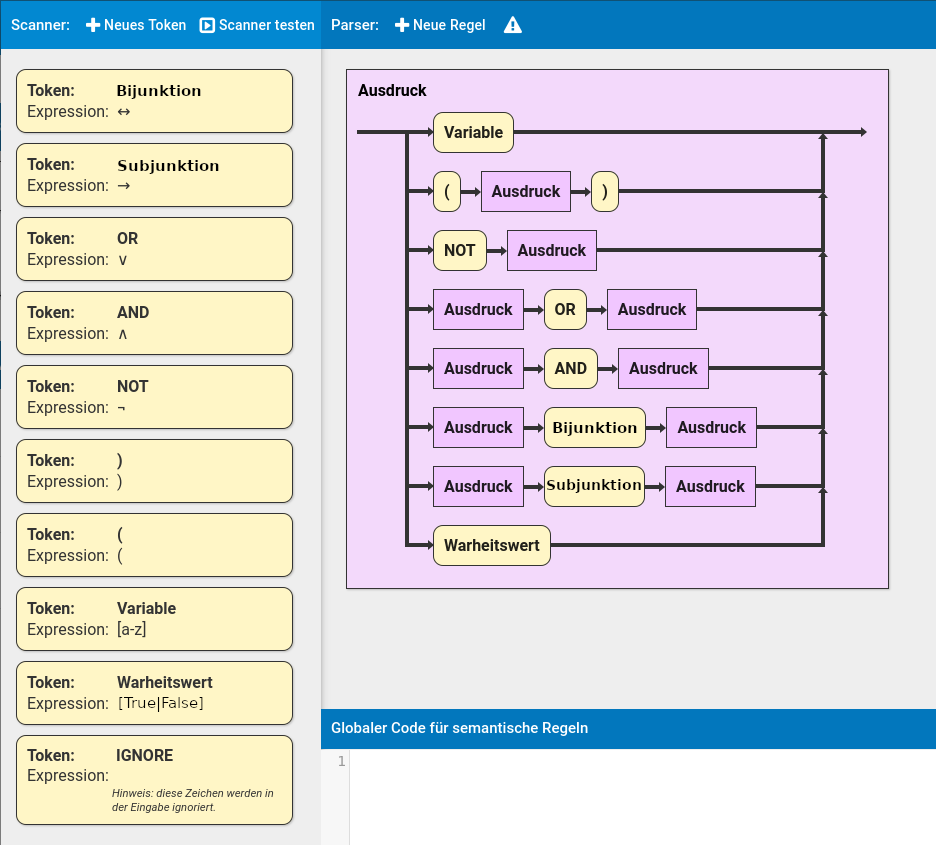
Interpreter für aussagenlogische Ausdrücke (FLACI)

Partielle Funktionen - Programmatisch umgesetztes Beispiel

import time x = float(input("Please type real number: ")) if x == 3: while True: time.sleep(1) else: print(35/(x-3))

ausführen

Selbstgewähltes Beispiel für eine partielle Funktion

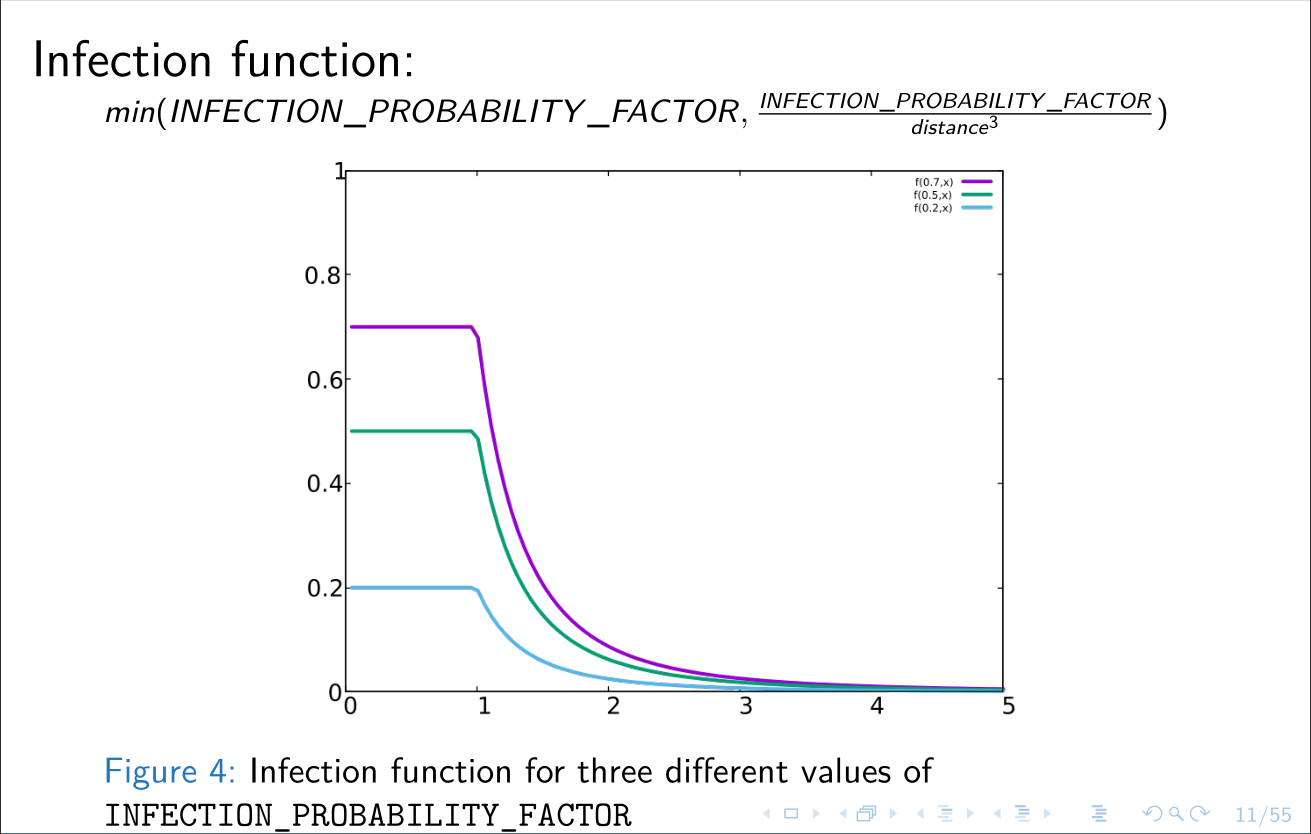
Infektionsfunktion, bei der die Infektionswahrscheinlichkeit von dem inversen Würfel (inverse cube) der Distanz zwischen den Individuen abhängt. Diese Funktion ist nur für positive x definiert, da es keine negative Distanz geben kann. Auch der Wertebereich ist hier beschränkt, die Infektionswahrscheinlichkeit darf einen Maximalwert nicht überschreiten, hier der INFECTION_PROBABILITY_FACTOR. In jedem Fall kann sie als Wahrscheinlichkeit nicht größer als 1 sein.

Abbildung aus Projektpräsentation einer Epidemiesimulation (von Uta Lemke und William Stock)

x-Achse: Distanz zwischen den Individuen

y-Achse: Infektionswahrscheinlichkeit in Prozent

Injektiv, Surjektiv, Bijektiv

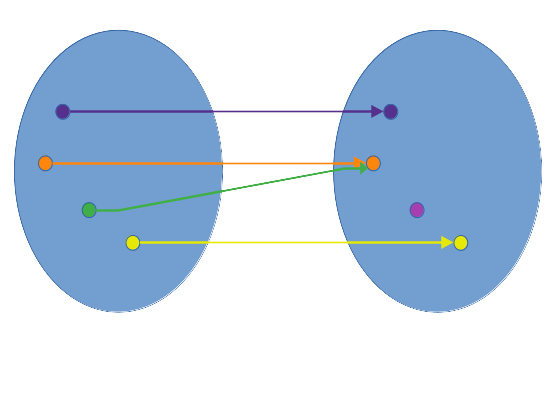
Injektiv

• für eine Funktion f: X → Y existiert für jedes y aus Y maximal ein Funktionswert x aus X
• 1 → 0..1 Relation

Beispiel:

IDs. Keine ID darf doppelt sein, sonst wäre es keine Identifikationsnummer. Es kann aber aus den möglichen ID-Kombinationen IDs geben, die nicht zugeordnet sind.

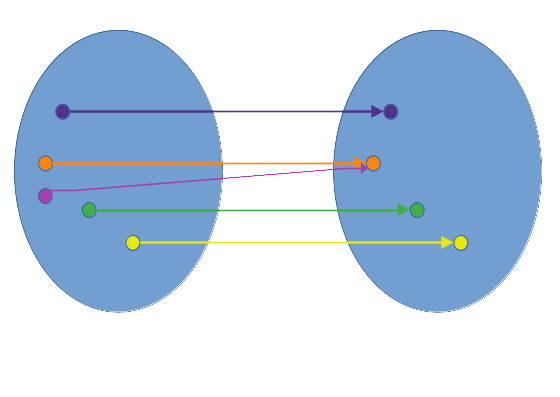
Surjektiv

• für eine Funktion f: X → Y existiert für jedes y aus Y mindestens ein Funktionswert x aus X
• 1 → 1..n Relation

Beispiel:

Bücher werden an Kinder verteilt. Manche Kinder müssen sich ein Buch teilen, da es nicht genug Bücher gibt. Also hat jedes Buch mindestens ein Kind, das es besitzt, manche werden aber auch von mehreren Kindern besessen.

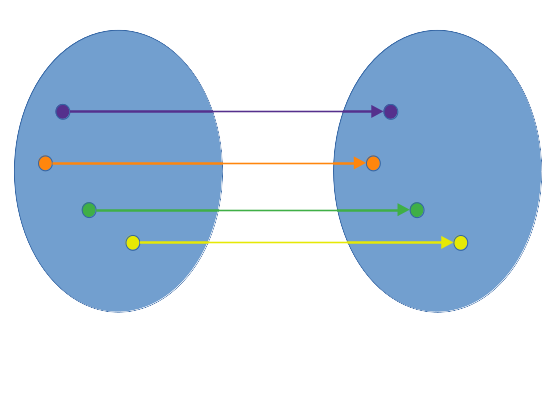
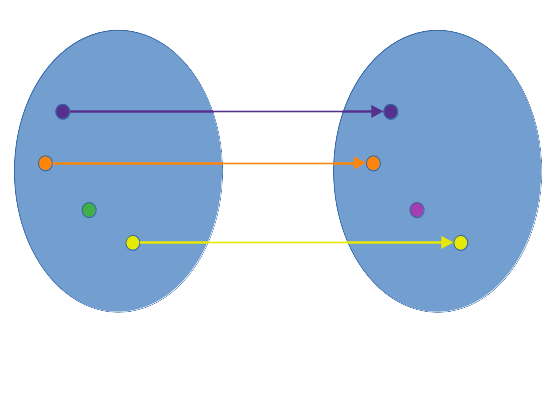
Bijektiv

• für eine Funktion f: X → Y existiert für jedes y aus Y genau ein x aus X
• 1 → 1 Relation

Beispiel:

Eine Match-Making-App, die jede Person, die an dem Programm teilnimmt, mit genau einer anderen matcht.

Injektiv und surjektiv

Injektiv, nicht surjektiv

Surjektiv, nicht injektiv

Bitte überprüfen!

Weder surjektiv, noch injektiv