Teile und Herrsche

Aus ProgrammingWiki

Wechseln zu: Navigation, Suche

Loading

Inhaltsverzeichnis

Teile und Herrsche (Divide and Conquer)

Definition

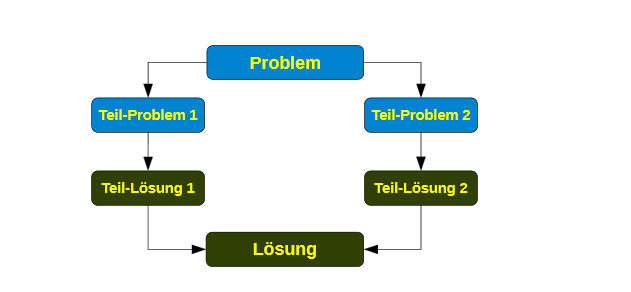
  • Das Entwurfsverfahren Teile und Herrsche dient dem Entwurf rekursiver Algorithmen.
  • Die Idee ist es, ein Problem der Größen in mehrere gleichartige, aber kleinere Teilprobleme zu zerlegen ( divide).
  • Aus rekursiv gewonnenen Lösungen der Teilprobleme ( conquer) gilt es dann, eine Gesamtlösung für das ursprüngliche Problem zusammenzusetzen .
  • Ziel dieser Methode ist es eine Effizienzverbesserung zu erreichen.


S3anbrem Anw.PNG

Entwurfsmethode für Algorithmen

1. Teile das Problem in kleinere Unterprobleme (Divide)
2. Löse rekursiv die entstehenden Unterprobleme (Conquer)
3. Setze die Lösungen zusammen.

Eigenschaften

  • kann bei konzeptionell schwierigen Problemen hilfreich sein
  • kann effiziente Lösungen realisieren
  • für Parallelverarbeitung geeignet

Effizienzbetrachtung

Die folgende Rechnung dient als Beweis, dass eine Effizienzverbesserung auftritt:
Wir nehmen an, dass ein bestimmter Algorithmus $\mathit{A}$ ein Problem mit $\mathcal{O}\left(n^{2}\right)$, also $\mathit{T}_{\mathcal{A}} \leq c \cdot n^{2} $ , löst. Für ein Algorithmus $\mathit{B}$, der drei dieser Probleme der Größe $\left( \frac{n}{2}\right)$ mit $\mathit{A}$ bearbeitet und mit $\mathcal{O}\left(n\right)$ zusammenfügt gilt:

\begin{align} \begin{array}{rcl} T_{B} \left( n \right) & = & 3 \cdot T_{A} \cdot\left( \left\lceil \frac{n}{2} \right\rceil \right) + d \cdot n\\\\ & \leq & 3 \cdot c \cdot \left( \frac{n+1}{2}\right) ^{2} + d \cdot n\\\\ & \leq & 3 \cdot c \cdot \left( \frac{n+1}{2}\right) \left( \frac{n+1}{2}\right) + d \cdot n\\\\ & \leq & 3 \cdot c \cdot \left( \frac{n^{2} + 2n + 1}{4}\right) + d \cdot n\\\\ & \leq & 3 \cdot c \cdot \left( \frac{n^{2}}{4} + \frac{2n}{4} + \frac{1}{4}\right) + d \cdot n\\\\ & \leq & \frac{3cn^{2}}{4} + \frac{6cn}{4} + \frac{3c}{4} + d \cdot n\\\\ & \leq & \frac{3}{4}cn^{2} + \frac{3}{2}cn + \frac{3}{4}c + d \cdot n\\\\ & \leq & \frac{3}{4}cn^{2} + \left(\frac{3}{2}c + d\right) \cdot n + \frac{3}{4} c\\\\ \end{array} \end{align} Man erkennt an den führenden Summanden, dass sich tatsächlich eine Effizienzsteigerung von ca. 25% ergibt. Allerdings liegt noch immer ein quadratischer Aufwand mit $\mathcal{O}\left(n^{2}\right)$ vor. Daher betrachten wir nun einen Algorithmus $\mathit{C}$ , welcher das Problem auf rekursive Art löst.

\begin{align} \mathit{T}_{\mathcal{C}}\left(n\right) = \begin{cases} \mathit{T}_{\mathcal{A}}\left(n\right), \mbox{$wenn$}\ n\leq n_{0} \\ \mathit{3\ T}_{\mathcal{C}}\left(\dfrac{n}{2}\right), \mbox{$sonst$}\end{cases} \\\\\ \mathit{T}_{\mathcal{C}}\left(n\right) = \mathit{3\ T}_{\mathcal{C}}\left(\dfrac{n}{2}\right) = \mathcal{O}\left(n^{log_{2}{3}}\right) = \mathcal{O}\left(n^{1.59}\right) \end{align} Nach dem Lösen dieser Formel kommen wir zu dem Ergebnis $\mathit{T}_{\mathcal{C}}\left(n\right)=\mathcal{O}\left(n^{1.59}\right)$.

Beispiel: Die Türme von Hanoi

Wenn die Anzahl der Scheiben 1 beträgt, ist die Lösung des Problems trivial.
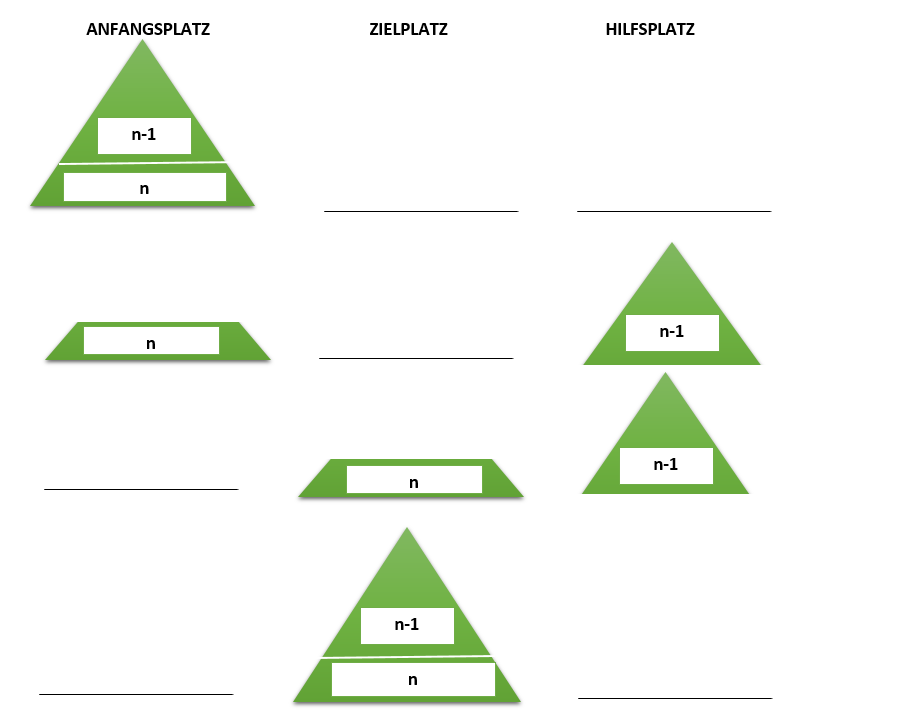
Bei mehr als einer Scheibe lässt sich das Gesamtproblem in drei Teilprobleme zerlegen:

  • Transportiere n-1 Scheiben vom Anfangsplatz auf den Hilfsplatz.
  • Transportiere die letzte Scheibe vom Anfangsplatz auf den Zielplatz.
  • Transportiere n-1 Scheiben vom Hilfsplatz auf den Zielplatz.

S3anbrem Azh.PNG

Übung: Die Türme von Hanoi

  • Transportiere n Scheiben vom Anfangsplatz auf den Zielplatz, unter Verwendung eines Hilfsplatzes.


S3anbrem U1.png

Spiel http://www.gf-webdesign.de/tuerme-von-hanoi/tuerme-von-hanoi.htm

Quicksort

Das Verfahren

Quicksort ist ein schneller Sortieralgorithmus auf der Basis rekursiver Vergleiche von Elementen, welcher von C.A.O Hoare im Jahre 1960 entwickelt wurde.

Das Prinzip ist eine gegebene Gesamtliste $G$ so in zwei Teillisten $L$ und $R$ aufzuteilen (divide), dass alle Elemente von $L$ kleiner (oder gleich) als ein Vergleichselement (Pivotelement) $v \in G$

und alle Elemente von $R$ größer (oder gleich) als $v$ sind.


Es existieren zwei Basisfälle:
1. : $G$ ist leer
2. : $G$ enthält nur ein einziges Element

Wird nun der Quicksort-Algorithmus auf jede der enstandenen Teillisten angewandt, ergibt sich dadurch die rekursive Verarbeitung. Es wird dann, nach endlich vielen Zerlegungen, einer der beiden Basisfälle erreicht.
Das bedeutet die Teillisten liegen dann sortiert vor (conquer). Letztlich setzt man die einzelnen Teillisten zu der sortierten Gesamtliste $G$$sortiert$ zusammmen (combine) und zwar genau in der Form: $G$$sortiert$ = $L$$sortiert$ $v$ $R$$sortiert$

Funktionaler Aufbau



Durch diese Prozedur entstehen die zwei Teillisten $L$ und $R$, die für die Unterscheidung der Relation in Bezug auf das Pivotelement benötigt werden.

Um nun den Algorithmus richtig anwenden zu können, bedarf es einer weiteren Prozedur, die die Vorhergehende immer wieder rekursiv aufruft und dabei jeweils auf $L$ und $R$ quicksort anwendet um diese zu sortieren.



Interne Suchverfahren

Quicksort kann in die Kategorie der internen Suchverfahren eingeordnet werden. Das sind Algorithmen die in-place arbeiten, was bedeutet sie benötigen keinen zusätzlichen Speicherplatz, da sie die Eingaben intern verarbeiten und diese dann mit den Ausgaben überschreiben.
Bei der vorherigen Implementierung wurde dies zu Gunsten der Veranschaulichung vernachlässigt. So wurden die Elemente von $G$, die die jeweilige Relation (>= $v$ oder <= $v$) erfüllen, in eine der beiden erzeugten Listen eingetragen. Im Erzeugen von $L$ und $R$ liegt also hier das Problem.

Um die Bedingung des Quicksort-Algorithmus ($l <= v <= r$) erfüllen zu können und den genannten Nachteil zu eliminieren, nutzt man die Idee, die die folgende Implementierung verfolgt. Zunächst um der Speicherplatzbildung entgegenzuwirken muss die Bildung der Teillisten in $G$ erfolgen. Um auf jedes Element zugreifen zu können, wird in der folgenden Implementierung ein Vektor $a$ verwendet.
Das Pivot erhält die erste Poition, also $a[0]$. Zusätzlich werden zwei Zeiger $l$ und $r$ initiiert, wobei $l = a[1]$ und $r = a[n-1]$.

In Einerschritten wird:

1. $l$ solange nach rechts verschoben bis $a[l] > v$ und
   $r$ solange nach links verschoben bis $a[r] < v$
2. wenn jeweils ein Element gefunden wurde, wird $a[l]$ mit $a[r]$ getauscht und die Zeigerbewegung fortgesetzt
3. ansonsten wird $a[r]$ mit $a[0]$ vertauscht und $a$ ausgegeben 
4. insofern die Elemente links bzw. rechts vom Pivotelement aus noch unsortiert sind, wiederhole Schritt 1

Visualisierung

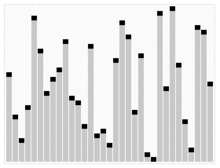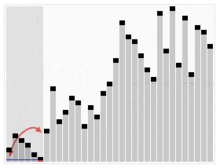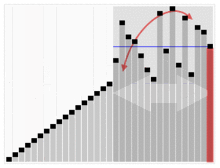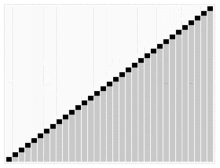
Die folgende Animation zeigt den verbildlichten Ablauf des Algorithmus:

roter Balken = Pivotelement p der jeweiligen Teilliste
blaue Linie = Wert von p

Quicksort animation.gif

Beispiel

Sortieren von (natürlichen) Zahlen:

In diesem Beispiel soll eine Liste $G$ =[6,13,3,7,9,7,2,1,15,10,5,6] mit Quicksort sortiert werden.
Es folgt eine ausführliche Lösung zum Erhalt der sortierten Liste:

Quicksort beispiel1a.png
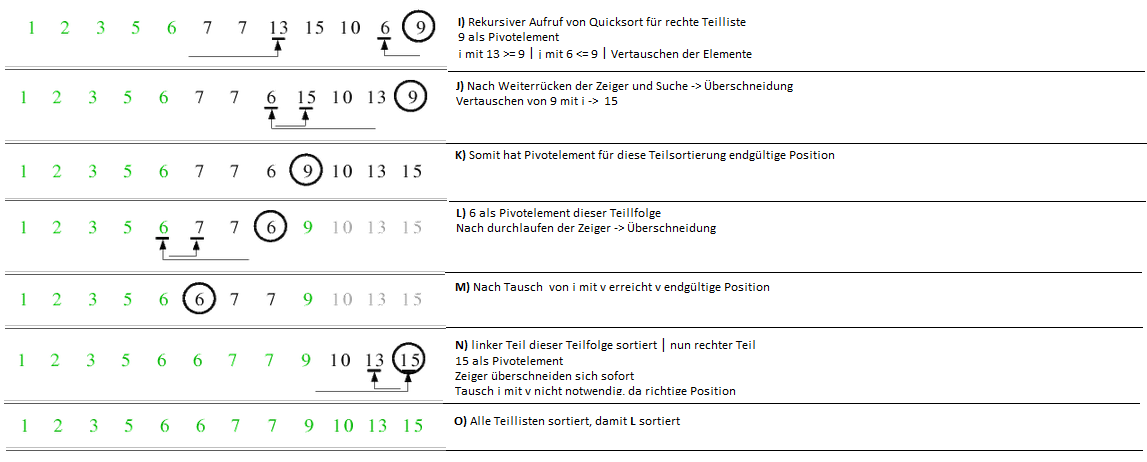
Quicksort beispiel1 2.png
Hinweis: Falls $j$ den Zeiger $i$ erreicht, kann dies schon zum Tausch von a[i] mit $v$ führen. Z.B. wenn a[0]>= $v$

Effizienz von Quicksort

Wegen Gründen der Vereinfachung zwecks Erklärung, wurde im Beispiel das letzte Element als Pivotelement gewählt, aber bei der Anwendung des Algorithmus sollte man auf die Wahl achten.
Wie effizient der Quicksort-Algorithmus ist, hängt nämlich in erster Linie von der Wahl des Pivotelementes ab.

Best-Case

Im besten Fall wird das Pivotelement so gewählt, dass dieses in der sortierten Liste genau in der Mitte liegt und somit die Gesamtliste $G$ aus (etwa) zwei gleich großen Listen besteht.

\begin{align} \mathit{T}\left(0\right) &= 0\notag\\ \mathit{T}\left(n\right) &= 2 \cdot \mathit{T}\left(\frac{n}{2}\right) + c \cdot n\notag \end{align}

Nach Auflösung mit der Meistermethode ergibt das einen Aufwand $T(n) = \mathcal{O}(n \ \log_{2} \ n)$ .


Average-Case

Im Durchnitt nimmt man an, dass die Wahrscheinlichkeit aller $n$ Teillistenlängen gleich ist. Somit ist die Wahl des Pivotelementes für jedes Element der Liste $G$ gleich wahrscheinlich.

\begin{align} \begin{array}{rcl} T(i) = T\left(n-i-1\right) = \frac {1}{n} \cdot \sum\limits_{j=0}^{n-1} T\left( j\right)\\\\ T(n) = \underbrace{T\left(i\right)}_{linke\ Teilliste} + \underbrace{T\left(n-i-1\right)}_{rechte\ Teilliste} + \underbrace{c \cdot n}_{Teillistenbildung}\\\\ \end{array} \end{align}

Nach Einsetzen ergibt sich folgendes:

\begin{align} \begin{array}{rcl} T\left(n\right) &=& \frac {2}{n} \sum\limits_{j=0}^{n-1} \ T\ \left(j\right) + c \cdot n\\\\ \end{array} \end{align}

Um die Summe zu beseitigen, werden folgende Differenzen gebildet:

\begin{align} \begin{array}{rcl} nT\left(n\right) &=& 2 \ \sum\limits_{j=0}^{n-1} \ T\ \left(j\right) + c \cdot n^{2} \\\\ \left(n-1\right)T\left(n-1\right) &=& 2 \sum\limits_{j=0}^{n-2}\ T\ \left(j\right) + c \cdot \left(n-1\right)^2 \mid \text{für} \ n:=n - 1; -\\\\ \\\\ nT\left(n\right) - \left(n-1\right)T\ \left(n-1\right) &=& 2T\ \left(n-1\right) + 2cn - c \mid -c\ \text{entfällt für}\ n \rightarrow \infty\\\\ \frac{T\left(n\right)}{n+1} &=& \frac{T\left(n-1\right)}{n} + \frac{2c}{n+1}\\\\ \frac {T\left(n-1\right)}{n} &=& \frac{T\left(n-2\right)}{n-1} + \frac{2c}{n}\\\\ \vdots & & \vdots\\\\ \frac{T\left(2\right)}{3} &=& \frac{T\left(1\right)}{2} + \frac{2c}{3}\\\\ \\\\ \frac{T\left(n\right)}{n+1} &=& \underbrace{\frac{T\left(1\right)}{2}}_{=0, da\ T\left(1\right) =0} + 2 \sum\limits_{i=3}^{n+1} \frac{1}{i}\\\\ \end{array} \end{align}

Bei der Benutzung der bekannten Schranken $\frac {\lfloor log_{2} \ n \rfloor +1}{2} < \mathit{H}_{n} \leq \lfloor log_{2} \ n \rfloor +1$ für die harmonischen Zahlen $\mathit{H}_{n} = \sum\limits_{k=1}^{n} \frac{1}{k}$ ergibt sich:

\begin{align} \frac {T\left(n\right)}{n+1} = \mathcal{O} \left(log_{2} \ n\right)\curvearrowright T\left(n\right) = \mathcal {O} \left(n \cdot log_{2} \ n\right) \end{align}


Worst-Case

Im schlechtesten Fall wird das Pivotelement so gewählt, dass dieses in der sortierten Liste entweder am Anfang oder am Ende liegt und somit auf der einen Seite das Pivotelement $v$ und auf der anderen Seite der Rest von $G$ liegt.
Dies ist z.B. der Fall, wenn $G$ vor der Anwendung von Quicksort bereits sortiert ist, das zu einem sehr langsamen Quicksort führt, was wiederrum zum einen aus Definitionssicht wiedersprüchlich erscheint und zum anderen aus Anwendersicht für Konfusion sorgt.

\begin{align} \mathit{T}\left(0\right) &= 0\notag\\ \mathit{T}\left(0\right) &= \underbrace{\mathit{T}\left(0\right)}_\text{= 0} + \mathit{T}\left(n - 1\right) + c \cdot n\notag \end{align}

Das kann mit der Iterationsmethode gelöst werden:

\begin{align} \mathit{T}\left(n - 1\right) &= \mathit{T}\left(n - 2\right) + c \left(n - 1\right)\notag\\ \mathit{T}\left(n - 2\right) &= \mathit{T}\left(n - 3\right) + c \left(n - 2\right)\notag\\\\ \vdots \\\\ \mathit{T}\underbrace{\left(\ n - k \ \right)}_{\text{ = 1 $\curvearrowright$ k = n - 1}} &= \mathit{T}\left(0\right) + c \left(n - k\right)\notag\\ \end{align}

Nach Einsetzten jedes Ausdrucks in die darüberliegende Zeile ergibt das:

\begin{align} \begin{array}{rcl} T(n) &=& c \cdot \sum\limits_{k=0}^{n-1} \left(n-k\right)\\\\ &=& c\cdot\left(\sum\limits_{k=0}^{n-1} n - \sum\limits_{k=0}^{n-1} k\right)\\\\ &=& c\cdot\left(n^2 - \frac {n-1}{2}\left(\left(n-1\right)+1\right)\right)\\\\ &=& c\cdot\left(n^2 - \frac {n^2 -n}{2}\right)\\\\ &=& c\cdot\left(\frac {n^2} {2} + \frac {n} {2}\right) \\\\\\ T(n) &=& \mathcal{O}\left(n^2\right)\\\\ \end{array}\notag \end{align}



Die Effizienz von Quicksort ist abhängig von der Anzahl der Elemente, da je länger die zu sortierende Liste wird, auch die Distanz steigt, aus der die Elemente miteinander vertauscht werden. Je kürzer also die zu sortierende Liste wird, desto ineffizienter arbeitet Quicksort, da es sich der Komplexität $\mathcal{O}(n^2)$ annähert.

Anpassung

Die bereits erwähnte Abhängigkeit des Algorithmus von der Wahl des Pivotelementes führt zu den eben berechneten Laufzeiten.
Dabei kann man die Wahl von $v$ durchaus beeinflussen, sodass z.B. die Wahrscheinlichkeit des Auftretens des Worst Cases verringert werden kann.
Außer Acht wird hierbei die Wahl des ersten oder letzten Elementes der Liste gelassen, da dies aus praktischer Sicht unzuverlässig ist.

Möglichkeit 1: $v$ als das mittlerste Element der Liste wählen
Möglichkeit 2: $v$ als ein zufällig gewähltes Element setzen
Möglichkeit 3: das erste, das mittlerste und das letzte Element der Liste nehmen und den Median dieser Drei als $v$ bestimmen.

Liste $L$ = [10,3,25,6,8,17,1,2,18,5]

Median aus den drei: [10,8,5] -> [5,8,10] ->8

Mergesort

Definition

  • Das Sortier­verfahren Mergesort erzeugt eine sortierte Folge durch Verschmelzen sortierter Teilstücke.
  • Das Verfahren beruht auf dem Divide-and-Conquer-Prinzip .
  • Die zu sortierende Folge
$L = \left(Le_{0}, Le_{1}, Le_{2}, \dots , Le_{n}, Re_{0}, Re_{1}, Re_{2}, \dots , Re_{m}\right)$

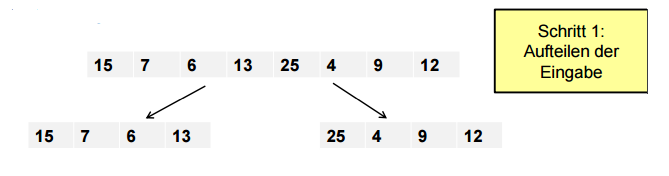
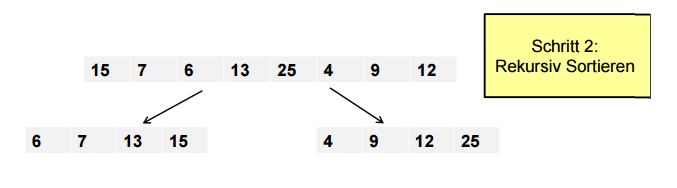
     wird zunächst in zwei Hälften aufgeteilt (divide), die jeweils für sich sortiert werden (conquer).

$TL = \left(Le_{0}, Le_{1}, Le_{2}, \dots , Le_{n}\right)$ und $TR= \left(Re_{0}, Re_{1}, Re_{2}, \dots , Re_{m}\right)$
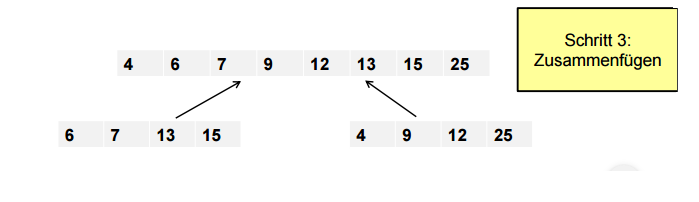
  • Dann werden die sortierten Hälften zu einer insgesamt sortierten Folge verschmolzen (combine).
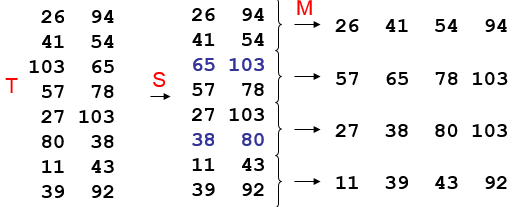
  • Die jeweiligen führenden Teilelemente $Le_{i}$ und $Re_{j}$ gelangen an ein "Tor". Wenn $Le_{i} < Re_{j}$ gilt, wird $Le_{i}$ durchgelassen und nimmt die nächste freie Position in der Gesamtliste ein. $Re_{j}$ wird anschließend mit $Le_{i+1}$ verglichen. Ansonsten natürlich umgekehrt.
  • Dieses Verfahren bietet die Möglichkeit einer iterativen Implementierung.

Vorteile

  • Geschickter Einsatz der Teile-und-Herrsche Technik.
  • Gutes Laufzeitverhalten für große Eingabegrößen
  • Die Stabilität

        Die relative Ordnung zweier Elemente , welche gleich sind , wird beibehalten.

  • sequenzielle Abarbeitung der Daten

Nachteile

  • der zusätzlich benötigte Speicher

Anwendung

  • Der Mergesort wird vor allem dann verwendet, wenn man eine große sortierte Datenmenge verwalten möchte.

Effizienzbetrachtung von Mergesort

  • Im Gegensatz zur Effizienzanalyse von Quicksort, gibt es bei Mergesort keine Unterscheidung zwischen Worst-, Best- und Average-Case, da hierbei nicht mit einem Pivot-Element gearbeitet wird, sondern die Listen immer in der Mitte geteilt werden.Der Algorithmus arbeitet immer gleich, egal ob eine Liste bereits sortiert ist oder nicht.
  • Je nach Implementierung erhält man für die Komplexität von Mergesort folgende Rekursionsgleichung:

                Sei $\mathit{T}\left(n\right)$ die Laufzeit von Mergesort.
                Das Aufteilen braucht $\mathcal{O}\left(1\right)$ Schritte.
                Die rekursiven Aufrufe brauchen $ 2\cdot \mathit{T}\left(\frac{n}{2}\right) $ Schritte.(ein Problem halbiert wird und man dadurch zwei halbe Probleme hat.)
                Das Mischen braucht $\mathcal{O}\left(n\right)$ Schritte.
                Um Mergesort zu analysieren, ist die Rekursionsgleichung : $\mathit{T}\left(n\right) = 2\cdot \mathit{T}\left(\frac{n}{2}\right) + \mathcal{O}\left(n\right)$, wenn n > 1 , mit $\mathcal{T(0)=0}$ und $\mathcal{T(1)=0}$ zu lösen.

  • Wir nehmen vereinfachend an, dass die Anzahl der Elemente $\mathit{n}$ eine Zweierpotenz ist.

\begin{align} &\mathit{T}\left(n\right) \leq 2 \cdot \mathit{T} \frac{n}{2} + n \\\\ &\leq 2 \cdot ( 2 \cdot \mathit{T} \frac{n}{4} + \frac{n}{2} ) + n = 4 \cdot \mathit{T} (\frac{n}{4}) + 2 n \\\\ &\leq 2^{log( \mathit{n})} \cdot \mathit{T} (\frac{n}{2^{k}}) + k \cdot n\\\\ & \leq 2^{log( \mathit{n})} \cdot \mathit{T} (1) + n \cdot log(\mathit{n}) \\\\ & = 0 + n \cdot log(\mathit{n})\\\\ & = n \cdot log(\mathit{n}) \\\\ \end{align}

Durch Anwendung des zweiten Falles der Meistermethode ergibt sich folgende Lösung:
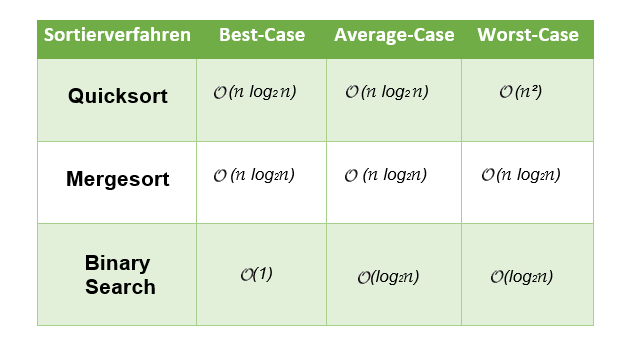
                Best-Case: $\mathit{T}\left(n\right) = \mathcal{O}\left(n\log_{2} n\right)$
                Average-Case: $\mathit{T}\left(n\right) = \mathcal{O}\left(n \log_{2} n\right)$
                Worst-Case: $\mathit{T}\left(n\right) = \mathcal{O}\left(n \log_{2} n\right)$

Visualisierung , Simulation, Animation

S3anbrem Mergesort-o.gif

[1] [2]


Pseudocode

  • Der folgende Pseudocode illustriert die Arbeitsweise des Algorithmus, wobei Liste die zu sortierenden Elemente enthält.

Schemeumsetzung Mergesort

Beispiele

Beispiel 1

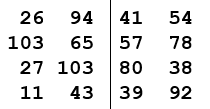
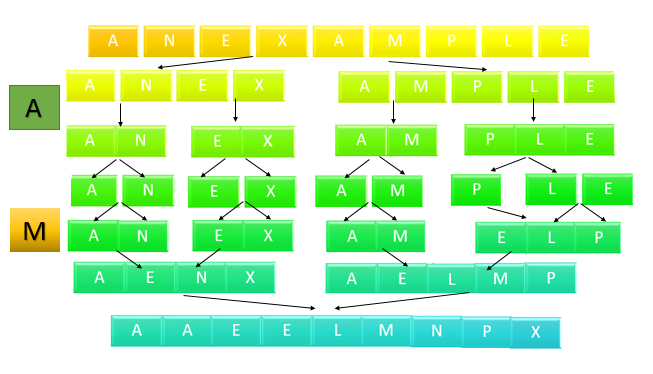
Im folgenden soll ein Array mit Mergesort sortiert werden:

S3anbrem Merge-sort-bsp1.PNG

Beispiel 2

S3anbrem Anexamplea.png

Suchalgorithmen

Sequenzielle Suche

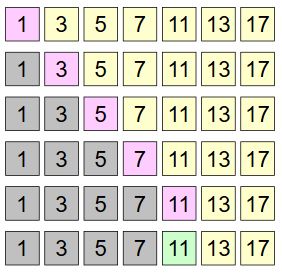
Die sequenzielle Suche oder auch als lineare Suche ist die Einfachste aller Suchmethoden. Bei dieser Methode wird von Anfang bis Ende jeder einzelne Eintrag nacheinander mit dem gesuchten Element $e$ verglichen. Sobald ein Listenelement mit $e$ übereinstimmt, endet der Algorithmus, sonst wird solange weitergesucht bis das Ende der Liste erreicht ist.
$e=11$ Kerich LineareSuche.JPG

Im Worst Case hat der Algorithmus hierbei ein Aufwand $T(n)=\mathcal{O}(n)$, da er jedes Element der Liste durchgehen muss.

Im Best Case beträgt der Aufwand $\mathcal{O}(1)$, da bereits das erste Element mit $e$ übereinstimmen kann.


Binäre Suche

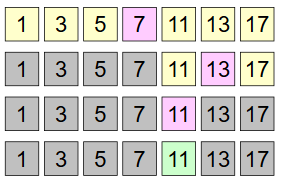
Das Binäre Suchen ist ein Teile-und-Herrsche-Verfahren. Dieses Verfahren ähnelt der linearen Suche, jedoch benötigt das binäre Suchen eine aufsteigend geordnete Liste.

Ablauf


1. Teile die Liste $G$ in der Mitte, sodass 2 gleichgroße Teillisten $L=[a_1,a_2,...,a_t]$ und $ R=[a_{t+1},...,a_n]$ entstehen.
    Für $t$ gilt $t=\frac{n}{2}$, wobei $t$ ganzzahlig ist. Wenn $t$ nicht ganzzahlig ist, wird der Wert abgerundet.
2. Vergleiche das erste Element der Teilliste $R$ mit $e$.

Falls $e = a_{t+1}$, dann wurde das Element gefunden.
Falls $e < a_{t+1}$, dann prüfe ob $L = null$, wenn ja dann wurde das Element $e$ nicht gefunden, sonst gehe zu Schritt 1 und verwende $L$ als neue Liste $G$.
Falls $e > a_{t+1}$, dann prüfe ob $R = null$, wenn ja dann wurde das Element $e$ nicht gefunden, sonst gehe zu Schritt 1 und verwende den Rest der Liste $R$ als neue Liste $G$.

Suchen des Elementes $e=11$:
Kerich BinarySearch.PNG

Effizienz

Best-Case

Der Best-Case endet wie beim sequenziellen Suchen mit dem ersten verglichenen Eintrag in der Liste. Somit haben diese beide Algorithmen den gleichen Aufwand im Best-Case von $T(n)=\mathcal{O}(1)$.

Average-/Worst-Case

Die Listen werden immer in der Hälfte geteilt, somit können immer die Hälfte der Werte ausgeschlossen werden. Geht man dabei vereinfacht von einer Anzahl von $n^2$ Elementen aus, so ist der Aufwand durch die permanente Teilung der Listen $T(n)=\mathcal{O}(log_2 n)$. Dies gilt sowohl für den Worst-, als auch für den Average-Case.

Implementierung in Scheme

Die Funktion teillisten spaltet die Liste $G$ in 2 Teillisten. binSuche ist für die binäre Suche zuständig.

Zusammenfassung

  • Teile und Herrsche - Zerlegung größerer Aufgaben oder Probleme in kleinere Aufgaben oder Probleme, die einfacher zu bewältigen oder leichter gelöst werden können.

  • Quicksort - schneller und rekursiver Sortieralgorithmus.
    • Es wird ein Pivotelement gewählt, sowie zwei Zeiger gesetzt, die sich aufeinander zubewegen. Dabei findet ein Austausch nach Überprüfung der Bedingung statt.
    • Obwohl der Algorithmus einen schlechten Worst-Case hat, dessen Wahrscheinlichkeit verringert werden kann, nutzt man ihn aufgrund des relativ guten Durchschnitts häufiger in der Praxis als andere Algorithmen.

  • Mergesort - ein schnelles (und rekursives) Sortierverfahren.
    • Ein Feld wird in zwei Teilfelder aufgeteilt, die dann rekursiv sortiert werden. Anschließend werden diese sortierten Teilfelder wieder zu einem Feld zusammengefügt. Dabei macht man sich zu Nutze, dass die beiden Teilfelder bereits sortiert sind.
    • Mit einer Zeit­komplexität von Θ(n log(n)) ist das Verfahren immer optimal.

  • Binäres Suchen - schnelles, rekursives Suchverfahren
    • Es muss eine sortierte Liste vorhanden sein, die immer wieder in der Mitte gespalten wird und mit dem ersten Element der rechten Liste verglichen.
    • Im Gegensatz zur sequenziellen Suche, die einen Aufwand von \mathcal{O}(n) hat, besitzt die binäre Suche selbst im Worst-Case einen Aufwand von $\mathcal{O}(log_2 n)$


S3anbrem Sortierung-mqb.png

Übungen

Übung 1 : Hanoi Java-Code

Pseudo - Code

Java-Code

  • Schreiben Sie Java-Code für Hanoi, auf der Grundlage dieses Pseudocodes .
  • Denken Sie auch an die Klasse Main, welche die Methode turm benutzt.


Lösung

Übung 2

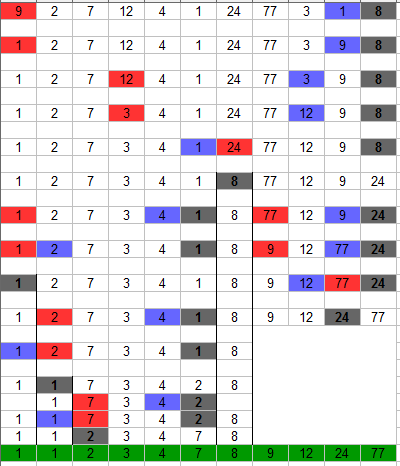
  • Sortieren Sie folgende Listen mit dem Quicksort-Algorithmus:

a) [9,2,7,12,4,1,24,77,3,1,8]

b) [2,5,3,7,1,9,8]


Übung 3

  • Sortieren Sie ein Array indem zwei Teilarrays sortiert und dann gemischt werden.

S3anbrem B1a1.PNG

Übung 4

Sortieren Sie die Buchstaben in der Zeichenkette aus Ihrem zusammengeschriebenen Vor- und Nachnamen mit Mergesort.

Übung 5

  • Schreiben Sie Java-Code für Merge Sort.


Lösung

Übung 6

Wenden Sie die binäre Suche auf das Resultat aus Aufgabe 2a) mit den folgenden Suchelementen an:
a) 7

b) 11

c) 3

Übung 7

Das Element $e=T$ soll in folgender Liste gesucht werden:

[A,C,E,G,J,L,M,N,P,Q,R,T,U,V,W,Z]
  • http://www.sorting-algorithms.com/

    Quellen

    Wagenknecht, 2003, Algorithmen und Komplexität
    Cormen, Leierson, Rivest und Stein, 2004, Algorithmen - Eine Einführung
    http://www.inf-schule.de/
    http://www.awb1.ch/
    http://www.ki.informatik.uni-frankfurt.de/
    http://ddi.cs.uni-potsdam.de/
    http://thm.de/
    http://de.wikiversity.org/
    http://www.roland-illig.de/
    https://de.wikipedia.org/wiki/Quicksort
    http://www.linux-related.de/index.html?/coding/sort/sort_quick.htm
    http://en.literateprograms.org
    http://www.sorting-algorithms.com/

    Von „https://programmingwiki.de/Teile_und_Herrsche“
    • Persönliche Werkzeuge