Sortieren

Aus ProgrammingWiki

Inhaltsverzeichnis 1 Vorbemerkungen 2 Grundlagen 3 Sortieren durch Auswählen (Minimumsuche) 4 Sortieren durch Einfügen 5 Sortieren durch Austauschen (Bubblesort) 6 Quicksort 7 weitere Sortierverfahren 8 Literatur

Vorbemerkungen

* Wir "sortieren" uns erst mal vor der Tür :-) ...

* Dann spielen wir Schiffe versenken

Grundlagen

Das Sortieren (und Suchen) ist in der Informatik umfassend untersucht worden, weil Sortieralgorithmen in zahlreichen Anwendungen verwendet werden
(Datenbanken, Compiler, Betriebssysteme etc.).

Grundsätzlich gibt es drei Methoden zum Sortieren:

• Auswählen

• Einfügen

• Austauschen

Wir besprechen diese Verfahren an Hand des Sortierens von Spielkarten: Beim Auswählen breitet man die Karten auf dem Tisch aus und wählt die niedrigste Karte. Anschließend wird die nächste Karte gewählt und hinter die niedrigste gereiht, usw. Beim Sortieren durch Einfügen hält man die Karten in der Hand, nimmt jeweils die nächste und fügt sie in einen am Tisch liegenden Stapel so ein, dass sie jeweils an der richtigen Stelle zu liegen kommt. Die Karten sind sortiert, sobald man keine Karte mehr in der Hand hält. Um die Karten durch Austauschen zu sortieren, breitet man die Karten in beliebiger Reihenfolge auf dem Tisch aus und tauscht dann die falsch liegenden Karten solange aus, bis der Satz geordnet ist.

Für die "Güte" eines Sortieralgorithmus sind folgende Kriterien ausschlaggebend:

  1.	Wie schnell sortiert der Algorithmus durchschnittlich Informationen? 
  2.	Wie schnell ist er im günstigsten und ungünstigsten Fall? 
  3.	Verhält sich der Algorithmus natürlich (d.h. hat er bei gut sortierten Listen 
        wenig und bei ziemlich ungeordneten Listen viel zu tun)? 
  4.	Ordnet er Elemente mit gleichen Schlüsseln um? 

Sortieralgorithmen bieten sich als grundlegendes Thema für die Analyse von Algorithmen an.

Sortieren durch Auswählen (Minimumsuche)

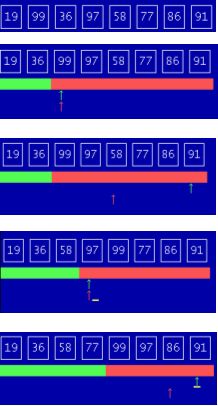
Die Idee einer der einfachsten Sortieralgorithmen ist die folgende: Finde zunächst das kleinste Element im Datenfeld und tausche dieses gegen das an der ersten Stelle befindliche Element aus. Anschließend finde das zweitkleinste Element, tausche es gegen das zweite Element aus ... usw.

Diese Sortiermethode ist für kleine Dateien sehr gut brauchbar. Zu beachten ist, dass jedes Element tatsächlich nur einmal getauscht wird.

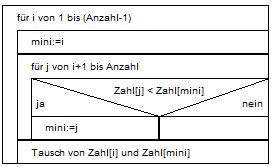
       Prinzip: Aus einer Menge wird das kleinste Element ausgewählt und mit dem ersten Element vertauscht.
       Diese Vorgänge werden wiederholt ,wobei die Anzahl der Elemente bei jeder Wiederholung von 
       vorn um eins verringert wird.
       Zuletzt werden nur noch zwei Elemente überprüft und gegebenenfalls vertauscht.

unsortiertes Feld 36 mit 99 vertauscht, anschließend kleinstes Element des Restfeldes (roter Pfeil) mit 99 vertauscht 77 mit 99 vertauscht, anschließend kleinstes Element des Restfeldes mit 99 vertauscht...

Implementiert könnte dies so aussehen:

procedure minimum(n:integer); var z:array[0..7] of integer; var i,j,k,h:integer; begin for i:=0 to 7 do begin z[i]:=random(20)+1; write(inttostr(z[i])+' '); end; for i:=0 to 7 do begin k:=i; for j:=i to 7 do if z[j]<z[k] then k:=j; h:=z[i]; z[i]:=z[k]; z[k]:=h; end; writeln(''); writeln(''); for i:=0 to 7 do write(inttostr(z[i])+' '); end;

minimum(8);

ausführen

Experimentieren Sie:
Ändern Sie den Bereich der Zufallszahlen
Verändern Sie die Größe des Feldes
Sortieren Sie eine beliebig große Menge - was muss alles verändert werden?

weitere anschauliche Hinweise auch zu Aufwand und Komplexität unter[[1]] (Achtung: Programmiersprache hier ist Scheme).

Sortieren durch Einfügen

       Prinzip: Man wählt ein Element (nacheinander vom zweiten bis zum letzten) und fügt es jeweils an die richtige 
       Stelle der davorstehenden geordneten Teilmenge ein. 

unsortiertes Feld; zweites Element herausgenommen und vor dem Ersten eingefügt sechstes Element genommen und als viertes eingefügt, dabei werden viertes und fünftes (alt) neues fünftes und sechstes Element Letztes Element an die richtige Stelle, Feld vollständig sortiert

Implementieren Sie das Sortieren durch Einfügen analog zum Sortieren durch Auswählen!

ausführen

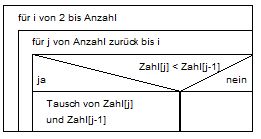
Sortieren durch Austauschen (Bubblesort)

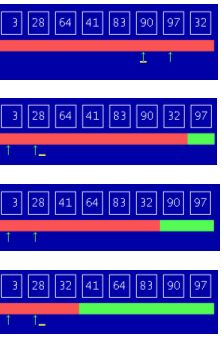
Dieses Sortierverfahren wird häufig erklärt, obwohl es wahrscheinlich das ungünstigste Sortierverfahren darstellt, das jemals realisiert worden ist: Durchlaufe immer wieder das Feld und vertausche jedesmal, wenn es notwendig ist, benachbarte Elemente. Die Datei ist sortiert, wenn kein Austausch mehr notwendig ist. Der Algorithmus erhält seinen Namen von der Tatsache, dass die Elemente - ähnlich wie Blasen im einem Glas Mineralwasser - aufsteigen, bis sie an der richtigen Stelle sind.

       Prinzip: Vom letzten Element einer Menge an werden jeweils zwei benachbarte Elemente verglichen und ausgetauscht, wenn
       sie falsch sortiert sein sollten. Dabei wandert da kleinste Element an die erste Stelle.
       Das Vergleichen und Austauschen wird mit Ausnahme dieses bereits richtig postierten Elements wiederholt.
       Das Sortieren kann aufsteigend (links nach rechts) oder absteigend (umgekehrt) erfolgen.

unsortiertes Ausgangsfeld, die 83 ist falsch sortiert und wird bis zum Feldindex, der einen Wert größer als 83 enthält, verschoben, anschließend wird die 97 und die 32 vertauscht, wonach die 97 als größte Zahl des Feldes als erste an der richtigen Stelle steht. Das Vergleichen beginnt wiederum von vorn, wobei die Zahlen 64 und 41 sowie 90 und 32 vertauscht werden. Die 90 steht damit als zweite Zahl an der richtigen Stelle. Anschließend wird die 32 nach links durchgereicht und das Feld ist vollständig sortiert.

Implementieren Sie Bubblesort analog zum Sortieren durch Auswählen!

ausführen

Quicksort

Das Sortieren durch Minimumsuche (MinSort) ist nicht sehr effizient.
Wir betrachten deshalb den nachfolgenden Algorithmus.

Beschreibung:

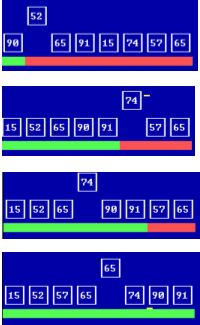
• Benutze das erste Element einer (numerischen) Liste als Trennelement.
• Erzeuge zwei Teillisten, deren Elemente kleiner bzw. größer als das Trennelement sind.
• Setze dieses Verfahren für jede nichtleere Teilliste fort und
• füge die sortierten Teillisten zur Gesamtliste zusammen.

Den so beschriebenen Sortieralgorithmus bezeichnet man als QuickSort (schnelles Sortieren). Er wurde 1962 von dem britischen Informatiker Sir Charles Antony Richard Hoare (* 11. Januar 1934) vorgestellt.

Prinzip	Quelltext in Pascal
		C.A.R. Hoare

procedure QUICK_SORT(lowerBound, upperBound: Integer); var i, j, KEY, X, Y:Integer; B: boolean; k: array[1..1000] of integer; begin B := true; If (lowerBound < upperBound) Then begin i := lowerBound; j := upperBound + 1; KEY := K[lowerBound]; while B do begin i := i + 1; while (K[i] < KEY) AND (i>upperBound) do i := i + 1; j := j - 1; while K[j] > KEY do j := j - 1; If i < j then begin X := K[i]; K[i] := K[j]; K[j] := X; end else B := false; end; Y := K[lowerBound]; K[lowerBound] := K[j]; K[j] := Y; QUICK_SORT(lowerBound,j - 1); QUICK_SORT(j + 1, upperBound); end; end;

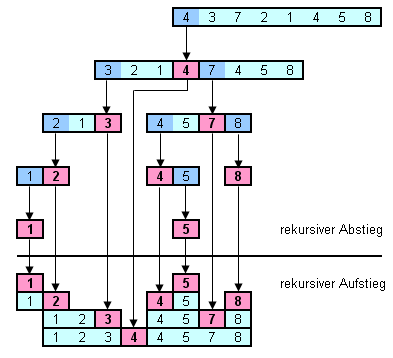Der Algorithmus arbeitet nach dem Prinzip Teile und Herrsche.
weitere Informationen unter: [2]

sowie sehr anschaulich zur Komplexität auch unter [[3]] (Achtung: Programmiersprache hier ist Scheme).

weitere Sortierverfahren

Mergesort [[4]]

Gnomesort [[5]]

Literatur

• Fahldieck, Karl-Heinz: Algorithmen, Frankfurt am Main: Verlag Moritz Diesterweg, 1993
• Sedgewick, Robert: Algorithmen, Bonn:Addison-Wesley Publishing Company, 1992
• Hermann, Dietmar: Algorithmen Arbeitsbuch, Bonn; München; Paris, Addison-Wesley Publishing Company, 1992
• Junger, Hans u.a.: Informatik, Frankfurt am Main; Aarau, Verlag Moritz Diesterweg; Verlag Sauerländer AG, 1988