Hamilton Kreise Übung

Aus ProgrammingWiki

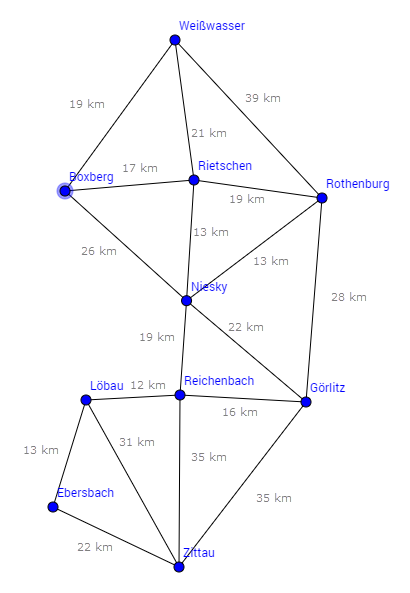
Übung Teil 1: Hamilton Graphen und Travelling Salesman Problem

Wir haben folgenden Graphen:

Aufgaben:

1. Stellen sie einen 2. Graphen auf, der die Fahrzeit beinhaltet. Die Durchschnittsgeschwindigkeit beträgt 70 km/h. (Mögliches Mittel: GeoGebra, Umrechner [1])
2. Erstellen Sie einen Hamiltonweg und einen Hamiltonkreis für den Graphen mit der Fahrzeit und der Strecke. Ihr Startpunkt wird Ihnen zugeteilt [2]. Geben Sie zum Vergleich die Länge bzw. die Gesamtfahrzeit des Kreises bzw. Graphen an. Tragen Sie diese Ergebnisse in die Datei [3] ein.
3. Markieren Sie eine Dreiecksungleichung.
4. Nehmen sie den Teilgraphen der aus folgenden Knoten besteht (Löbau, Ebersbach, Zittau, Görlitz, Reichenbach) und erweitern ihn zu einem vollständigen Graphen.
5. Wenden sie auf diesen Graphen die nearest neighbor Heuristik an und Geben sie alle möglichen Touren an und die Kosten der jeweiligen Tour.
6. Nehmen sie als Referenz die optimale Tour. Berechnen sie anhand der schlechtesten Lösung wie weit diese vom Optimum abweicht, die Angabe soll in Prozent erfolgen.

Hilfe für Aufgabe 4

Gawantka.falko_Entfernungen.pdf (0.1 MB)

Zusatzaufgabe:

1. Entwickeln sie einen Pseudocode für die erschöpfende Suche.

2. Nutzen sie die Implementation der nearest neighbor Heuristik aus der Vorlesung und die Methode buildTestMatrix und gegebenenfalls weitere Methoden um ein lauffähiges Programm zu erstellen, mit welchen sie eine empirische Effizienz Analyse für die nearest neighbor Heuristik durchführen können. Wählen sie die Problemgrößen selbst und führen die Analyse für je 10 Probleminstanzen durch.

public static int[][] buildTestMatrix(int index) { String[] out = {"Test"}; int n = index; Random r = new Random(); int[][] matrix = new int[n][n]; String output = ""; int compareInt = 0; for (int i = 0; i < matrix.length; i++) { for (int j = 0; j < matrix[i].length; j++) { matrix[i][j] = r.nextInt(1000)+1; } } for (int i = 0; i < matrix.length; i++) { for (int j = 0; j < matrix[i].length; j++) { if (i == j) { matrix[i][j] = 0; } } } for (int i = 0; i < matrix.length; i++) { for (int j = i+1; j < matrix[i].length; j++) { compareInt = matrix[i][j]; if (matrix[j][i] == compareInt) { } else { matrix[j][i] = compareInt; } } } return matrix; }