Zeitaufwand und asymptotische Ordnung
Aus ProgrammingWiki
Wir haben bisher den Zeitaufwand der sequenziellen und binären Suche empirisch untersucht.
Nun wollen wir durch allgemeine Überlegungen die Funktionen $T:\mathbb{N} \rightarrow \mathbb{R}^+$ bestimmen, die den Zeitaufwand der Algorithmen analytisch beschreiben. Vergleichbare Aufwandsfunktionen sollen zu einer Aufwandsklasse zusammengefasst werden.
Inhaltsverzeichnis |
Zeitaufwand bei der sequenziellen Suche
Die empirischen Untersuchungen unserer sequenziellen Suche ergaben: $T(n) \approx 0,64 \cdot n$.
Wir beachten dabei, dass die gesuchte Zufallszahl nicht in jedem Fall Element der Zufallsliste gewesen sein muss.
Bei der Suche eines Elements, das stets im Suchraum enthalten ist, gilt: $T(n) = \tfrac{n}{2}$.
Für sehr große $n$ wird es aber nebensächlich, wie groß der Faktor $k$ in der Funktion $T(n) = k \cdot n$ ist. In beiden Fällen wächst der Zeitaufwand linear mit der Problemgröße.
Da wir bei Komplexitätsuntersuchungen an Aussagen wie:
"Wenn $n$ ver-$x$-facht wird, dann ver-$y$-facht sich der Zeitaufwand."
interessiert sind, sollen deshalb konstante Faktoren und Summanden keine Rolle spielen.
Asymptotische Ordnung
Definition:
Die asymptotische Ordnung $\mathcal{O} (f)$ einer Funktion $f:\mathbb{N} \rightarrow \mathbb{R}^+$ beschreibt die Menge aller Funktionen $t:\mathbb{N} \rightarrow \mathbb{R}^+$, für die bei hinreichend großem $n$ gilt:
$t(n) \le c \cdot f(n), \hspace{0.3em} c \in \mathbb{R}^+$.
Mit der so genannten $\mathcal{O}$-Notation lassen sich also Algorithmen hinsichtlich ihres Zeitaufwandes klassifizieren. $\mathcal{O}$ heißt Landau-Symbol, benannt nach dem deutschen Zahlentheoretiker Edmund Georg Hermann Landau (* 14. Februar 1877; † 19. Februar 1938).
Beispiel:
Für die sequenzielle Suche schreibt man: $T(n) = \mathcal{O}(n)$.
Zeitaufwand bei der binären Suche
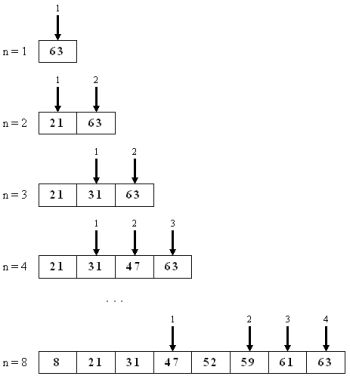
Bei der binären Suche vermuten wir einen logarithmischen Zeitaufwand. Um auch hier eine anschauliche Erklärung zu finden, konzentrieren wir uns zunächst auf die maximale Anzahl der notwendigen Teilungen (Worst-case-Fall):
Bereits nach wenigen Beispielen lässt sich für den Worst-case-Fall vermuten: $2^{T-1}=n$.
Wir wollen diese Vermutung mit der Prozedur binsuche-worst-case untermauern. Diese Prozedur zählt die in einer vorgegebenen Intervallgröße möglichen Halbierungenschritte bis zur elementaren Intervallgröße $1$.
Mit der variabelstelligen Prozedur tabausgabe wird das entsprechende Werkzeug zur Bildschirmausgabe bereit gestellt:
Für den Worst-case-Fall können wir unsere Vermutung bestätigen. Es gilt offensichtlich:
$2^{T-1}=n$ und damit:
$T(n) = \log_2 n + 1$
Doch wie verhält sich die binäre Suche im Mittel (Average-case-Fall)?
Wir definieren dazu Prozeduren, die nur noch die Anzahl der benötigten Versuche beim Raten einer Zahl bestimmen bzw. auswerten sollen:
Ergänzen Sie die Prozedur computerraten-worst-case, die im Intervall $[1;max]$ bei einer vorgegebenen Anzahl von Simulationen die höchste Anzahl der benötigten Versuche zum Raten einer Zahl ermittelt.
Quelltext überprüfen:
Im Average-Case-Fall benötigt die binäre Suche bei hinreichend großem $n$ wenigstens einen Versuch weniger als im Worst-Case-Fall.
Wir können also verallgemeinern:
$T(n) = \log_2 n$ bzw.:
$T(n) = \mathcal{O}(\log_2 n)$
Zusammenfassung
Für Suchalgorithmen haben wir zwei Aufwandsklassen kennen gelernt:
| sequenzielle Suche: | $T(n) = \mathcal{O}(n)$ |
| binäre Suche: | $T(n) = \mathcal{O}(\log_2 n)$ |
Wir wollen uns die funktionalen Zusammenhänge deutlich machen: