Prozeduren

Aus ProgrammingWiki

Wechseln zu: Navigation, Suche

Inhaltsverzeichnis

Definition von Prozeduren

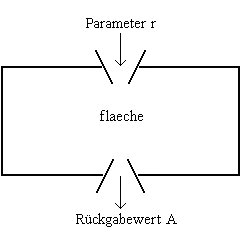
Um Kreisflächen beliebiger Radien zu bestimmen, war bisher immer die Neudefinition des Radiuses notwendig.
Wie kann der Radius als Argument übergeben werden?

Lösungsidee:

Definiere eine Prozedur, die ähnlich einer mathematischen Funktion einen Funktionswert zurückgibt.

Mathematik:

$flaeche: r \longrightarrow \pi \cdot r^2$
oder:
$flaeche(r) = \pi \cdot r^2$
 
Funktionsorientierte Programmierung:

Flaechenberechnung.gif

Implementation:

Wir überzeugen uns zunächst davon, dass wir tatsächlich eine Prozedur definiert haben:

Nun können wir Berechnungen mit beliebigen Radien vornehmen:

Interpretation:

  • Die Prozedur (lambda (r) (* pi r r)) wird an den Namen flaeche gebunden.
  • Der Parameter r heißt gebundene Variable.
  • Die Variablen * und pi sind dagegen ungebunden oder frei.

Beachte:
Die Bindung einer Prozedur an einen Namen heißt Prozedurabstraktion. Sie ist aber nicht notwendig!
In Scheme können auch unbenannte Prozeduren verwendet werden:

Zusammenfassung

  • Benutzerdefinierte Prozeduren werden mit λ-Ausdrücken definiert.
  • Allgemeine Syntax: (lambda (<Parameter>) <Body>).
  • Die Anzahl der Parameter kennzeichnet die Stelligkeit einer Prozedur. Ist die Parameterliste leer, spricht man von nullstelligen Prozeduren,
  • Die Parameter sind gebundene Variablen, die beliebig bezeichnet werden können, sofern sie nicht mit freien Variablen im Körper übereinstimmen.
  • λ-Ausdrücke können an Prozedurnamen gebunden werden (Prozedurabstraktion).

Aufgaben

  1. Sinnvolles Runden

    Für alle nachfolgenden Berechnungen ist es sinnvoll, über eine Prozedur zu verfügen, die auf eine beliebige Anzahl von Nachkommastellen rundet.
    Beispiele: 

    (runden 12.3456 2)  --> 12.35
(runden 0.005712 3) --> 0.006

    Nutzen Sie zur Implementation die Standard-Prozedur round, die lediglich ganzzahlig rundet.

     

    Quelltext überprüfen:

  2. Vollzylinder

    Schreiben Sie eine Prozedur zur Volumenberechnung eines geraden Vollzylinders.

     

    Quelltext überprüfen:

  3. Hohlzylinder

    Implementieren Sie nun eine Prozedur zur Volumenberechnung eines geraden Hohlzylinders.

     

    Quelltext überprüfen:

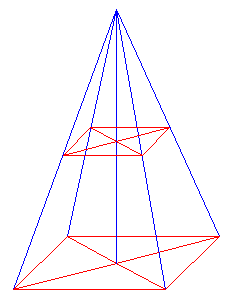
  4. Pyramide und Pyramidenstumpf

    Definieren Sie zunächst die Prozedur zur Berechnung des Volumens und der Oberfläche gerader quadratischer Pyramiden.

     

    Quelltext überprüfen:

     

    Quelltext überprüfen:

    Pyramide1.gif

    In einer nun geringeren Höhe wird die Spitze der quadratischen Pyramide abgeschnitten.
    Zurück bleibt ein Pyramidenstumpf.
    Schreiben Sie zwei Prozeduren, die entsprechend dieser Vorstellung das Volumen und den Oberflächeninhalt des Pyramidenstumpfes ermitteln.

     

    Quelltext überprüfen:

     

    Quelltext überprüfen:

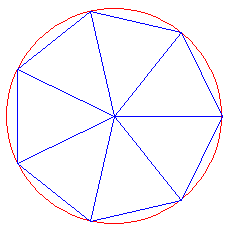
  5. Regelmäßiges N-Eck

    N Eck1.gif

    Zu einem regelmäßigen N-Eck sind der Außenradius $r$ und die Eckenzahl $N \geq 3$ gegeben.
    Implementieren Sie zwei Prozeduren zur Berechnung des Umfangs und des Flächeninhalts dieses N-Ecks.

     

    Quelltext überprüfen:

     

    Quelltext überprüfen:

Von „https://programmingwiki.de/Grundlagen_der_funktionsorientierten_Programmierung_mit_SCHEME/Prozeduren“
Persönliche Werkzeuge