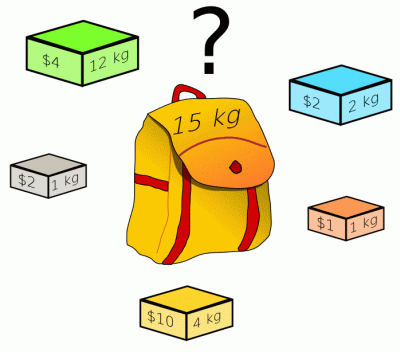Grenzen beim Problemlösen

Aus ProgrammingWiki

Inhaltsverzeichnis 1 Algorithmisch unlösbare Probleme 1.1 Halteproblem 2 Praktisch unlösbare Probleme 2.1 Schachcomputer 2.2 Ackermannn-Peter-Funktion 3 P-Probleme und NP-Probleme 3.1 NP-vollständige Probleme

Algorithmisch unlösbare Probleme

Halteproblem

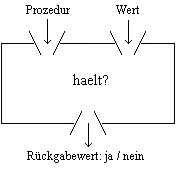
Zur Analyse eigener Programme wäre das Prädikat haelt? mit folgender Eigenschaft hilfreich:

Definition: $\mbox{haelt?}=\begin{cases}ja,\hspace{0.3em}\mbox{wenn}\hspace{0.3em}(\mbox{proz}\hspace{0.3em}wert)\hspace{0.3em}\mbox{stoppt}\\nein,\hspace{0.3em}\mbox{sonst}\end{cases}$

Der praktische Nutzen eines solchen Prädikats wäre unbestritten: Wir könnten beispielsweise versteckte Endlos-Rekursionen in fehlerhaften Prozeduren aufdecken!
Eine erste, naive Implementation wenden wir auf die Prozedur zur Fakultätsberechnung an:

(define haelt? (lambda (proz wert) (if (proz wert) #t #f))) (define fak (lambda (n) (if (= n 0) 1 (* n (fak (- n 1))))))

(haelt? fak 10)

ausführen

Es ist aber klar, dass im besagten Fall einer Endlos-Rekursion unser Prädikat seinen Dienst versagt. Die Abarbeitung würde über die Bedingungsprüfung (proz wert) nie hinausgehen und demzufolge den gewünschten Rückgabewert #f nicht liefern.
Das lässt den Verdacht aufkommen, dass die vollständige Implementation eines solchen Prädikats generell unmöglich ist.
Wir wollen diese Vermutung beweisen und definieren dazu zwei weitere Prozeduren:

(define endlos (lambda () (endlos))) (define seltsam (lambda (proz) (if (haelt? seltsam proz) (endlos) 'ok)))

Beweis:

Angenommen, das Prädikat haelt? existiert mit der oben genannten Eigenschaft tatsächlich, dann ergeben sich für den nachfolgenden Prozeduraufruf zwei mögliche Fälle:

(seltsam seltsam)

• Fall 1:
  (haelt? seltsam seltsam) liefert den Wert #t (d.h. seltsam stoppt), dann verbleibt seltsam in einer Endlos-Rekursion. Widerspruch!
• Fall 2:
  (haelt? seltsam seltsam) liefert den Wert #f (d.h. seltsam stoppt nicht), dann kommt seltsam mit der Rückgabe des Symbols 'ok zum Ende. Widerspruch!

In beiden Fällen kommt es zum Widerspruch zur Annahme. Es existiert also kein Prädikat zur Entscheidung des Halteproblems.
Wir müssen feststellen: Es gibt absolut unlösbare Probleme.

Praktisch unlösbare Probleme

Schachcomputer

Es hat viele Jahre gedauert, ehe mit enormem Aufwand ein Schachprogramm vorgelegt werden konnte, das sich mit einem Weltklassespieler messen konnte.
Dabei ist der erforderliche Algorithmus einfach:
Erzeuge zu jedem Zug des Gegners alle nach den Spielregeln mögliche Gegenzüge. Danach erzeuge alle Antwortzüge des Gegners usw.
Unter der Annahme, dass es in jeder Stellung nur 5 Fortsetzungsmöglichkeiten für den nächsten Spielzug gibt, ein Spiel im Mittel aus 60 Zügen (120 Halbzügen) besteht und zur Speicherung jedes Zustandes nur ein Byte gebraucht wird, würde der gesamte Speicherbedarf

$5^0+5^1+5^2+ ... +5^{120} = 1 \cdot \frac{5^{121}-1}{5-1} \approx 9.404 \cdot 10^{83} \mbox{Byte}$

betragen. Zumindest in den nächsten Jahren wird es nicht gelingen, den kompletten "Schachbaum" zu speichern. Der gewaltige Aufwand an Rechenzeit und Speicher verhindert eine praktische Realisierung.

Ackermannn-Peter-Funktion

Es ist möglich, algorithmisch prinzipiell lösbare Probleme anzugeben, die auch von zukünftigen "Supercomputern" nicht bewältigt werden können. Ein Beispiel ist die Ackermann-Peter-Funktion, benannt nach dem deutschen Mathematiker Wilhelm Friedrich Ackermann (* 29. März 1896; † 24. Dezember 1962) und der ungarischen Mathematikerin Rózsa Péter (* 17. Februar 1905; † 16. Februar 1977):

(define ack (lambda (n m) (cond [(= n 0) (+ m 1)] [(= m 0) (ack (- n 1) 1)] [else (ack (- n 1) (ack n (- m 1)))])))

Achtung! Prozedur nur mit sehr kleinen Werten für n und m testen!

(ack 3 6)

ausführen

Dabei handelt es sich um eine extrem schnell wachsende Funktion, die für die Klassifikation berechenbarer Funktionen eine große Bedeutung besitzt.
Die nachfolgende Tabelle veranschaulicht einige Funktionswerte:

n \ m	0	1	2	3	4	5	...
0	1	2	3	4	5	6	...
1	2	3	4	5	6	7	...
2	3	5	7	9	11	13	...
3	5	13	29	61	125	253	...
4	13	65533	...	...	...	...	...
5	65533	...	...	...	...	...	...
...	...	...	...	...	...	...	...

Bereits der Funktionswert von (ack 4 2) besitzt 19729 Dezimalstellen!
Sollte mit einem Computer die Berechnung (ack n m) möglich sein, so wird es immer einen Funktionswert (ack (+ n 1) (+ m 1)) geben, dessen Berechnung nicht mehr möglich ist. Es gibt also objektive Grenzen bei praktischen Problemlösungen.

P-Probleme und NP-Probleme

Problemen sieht man im Allgemeinen nicht an, ob sie bezüglich ihres Zeitaufwands schwer oder leicht lösbar sind.
Mitunter führt eine geringe Abweichungen in der Formulierung vergleichbarer Problemstellungen dazu, dass der Zeitaufwand zur Lösung fundamental verschieden ist, z.B.:

leicht, d.h. in $\mathcal{O}(n^k),k \ge 1$	schwer, d.h. in $\mathcal{O}(k^n),k > 1$
Finde den kürzesten Weg zwischen zwei Orten A und B in einem Straßennetz mit angegebenen Entfernungen.	Finde den längsten Weg zwischen zwei Orten A und B in einem Straßennetz mit angegebenen Entfernungen.

Die Klasse der leichten Probleme heißen P-Probleme. Als NP-Probleme bezeichnet man schwere Probleme.

P ist die Klasse von Problemen, die mit deterministischen Algorithmen in polynomialer Zeit gelöst werden können.
Die Klasse der NP-Probleme ist die Menge aller Probleme, die nichtdeterministisch in Polynomialzeit gelöst werden können.

Wie muss man sich eine nichtdeterministische Problemlösung vorstellen?

• 1. Schritt: Der Algorithmus "errät" einen Lösungskandidaten.
• 2. Schritt: Der Algorithmus verifiziert, ob der Kandidat tatsächlich eine Lösung ist.

Beide Schritte erfordern einen polynomialen Zeitaufwand.
Jedes Problem aus P liegt auch in NP. Es konnte aber bisher nicht gezeigt werden, dass es ein Problem gibt, das nachweislich zu NP aber nicht zu P gehört.
Damit ist offen, ob

$\mbox{P}=\mbox{NP}$ oder $\mbox{P}\subset\mbox{NP}$

gilt. An die Äquivalenz beider Klassen glaubt allerdings niemand.

NP-vollständige Probleme

Es gehört zu den herausragenden Leistungen der theoretischen Informatik, die schwersten Probleme zu einer separaten Klasse mit folgender Eigenschaft zusammenfassen zu können: Diese Probleme können in polynomialer Zeit ineinander überführt werden. Probleme dieser Klasse heißen NP-vollständig.
Sollte es je gelingen, einen effizienten (d.h. deterministisch polynomialen) Lösungsalgorithmus für ein Problem dieser Klasse zu finden, lassen sich auf einen Schlag alle Probleme dieser Klasse effizient lösen.
Derzeit sind mehr als 1000 NP-vollständiger Probleme bekannt. Dass es bisher nicht gelungen ist, einen effizienten Lösungsalgorithmus zu finden, spricht für die Vermutung $\mbox{P}\subset\mbox{NP}$.

Einige Beispiele für NP-vollständige Probleme:

• Rucksackproblem:
  Verschiedene Gegenstände sind mit ihrem Gewicht und ihrem Nutzwert gegeben. Eine Auswahl soll in einen Rucksack mit vorgegebenem Maximalgewicht gepackt werden, so dass der Gesamtwert der eingepackten Gegenstände maximal wird.
• Problem des Handlungsreisenden:
  Die Reihenfolge für den Besuch mehrerer Orte so zu wählen, dass die gesamte Reisestrecke des Handlungsreisenden nach der Rückkehr zum Ausgangsort möglichst kurz ist und jeder Ort nur einmal besucht wird.
• Stundenplanproblem:
  Eine Zuordnung von Klassen und Fachlehrern zu Unterrichtsräumen und -zeiten soll so vorgenommen werden, dass eine möglichst große Zahl an vorgegebenen Nebenbedingungen erfüllt wird.