Greedyalgorithmen und -heuristiken
Aus ProgrammingWiki
Inhaltsverzeichnis |
Einführung
Der Begriff "greedy" dient als Sammelbegriff für Problemlösungen, die in jedem Schritt "gierig" die momentan beste Fortführung, also eine lokale Optimallösung finden. Was im Praxisfall optimal ist, unterscheidet sich zwischen Themengebieten und Problemstellungen. Meistens soll eine abhängige Variable einen extremalen, also maximalen oder minimalen Wert annehmen.
Eine greedy-Herangehensweise unterscheidet sich außerdem darin wesentlich von anderen, z.B. naiven, Lösungen, dass einmal gewählte Möglichkeiten für die gesamte restliche Abarbeitung feststehen. Dies kann am Algorithmus von Dijkstra einfach gezeigt werden.
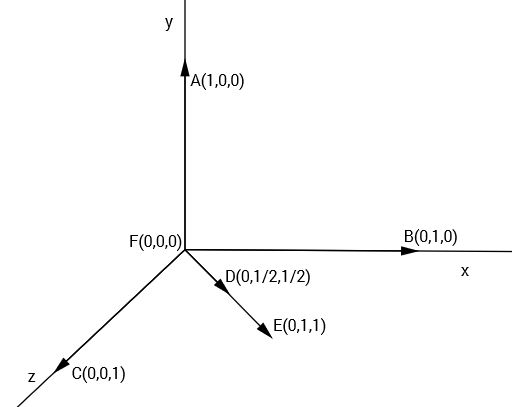
Vom Startknoten aus wird ein Baum aufgespannt, indem immer die Kante ausgewählt wird, die vom Startknoten aus den Weg mit dem geringsten Gewicht zu einem noch nicht abgearbeiteten Knoten dem Baum hinzufügt und der Endkniten des Weges als bearbeitet markiert. Wenn der Zielknoten erreicht ist, ist der Weg vom Start- zum Endknoten im erstellten Kürzeste-Wege-Baum auch der kürzeste Weg im Ursprungsgraphen Graphen vom Start zum Zeil.
Der Algorithmus von Prim arbeitet ähnlich. Hier werden nicht die kürzesten Wege vom Startknoten aus gesucht, sondern die kürzesten Verbindungen zum Baum.
Beide Verfahren sind eindeutig Algorithmen und liefern unter ihren jeweiligen Vorbedingungen die optimale Lösung. Für Matchingprobleme gibt es jedoch Algorithmen, für die das nicht zutrifft:
1 Setze $M := \varnothing$ 2 Wähle eine Kante $e \in E$, füge $e$ $M$ hinzu 3 Entferne $e$ und alle benachbarten Kanten aus $E$ 4 Falls $E \neq \varnothing$ gehe zu 2, sonst STOPP: $M$ ist maximal
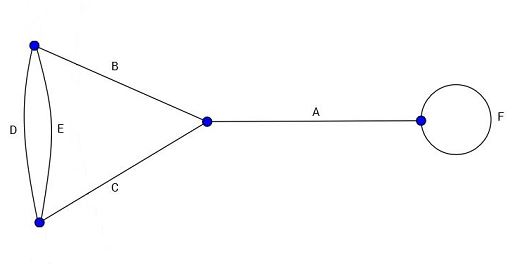
Das Ergebnis ist stets ein maximales Matching, in den unten stehenden Abbildungen ist aber ersichtlich, dass dieser Algorithmus unter Umständen kein perfektes Matching erreicht, obwohl dies möglich ist. Um ein perfektes Matching zu erreichen muss entweder eine Nachbearbeitung hinzugefügt oder der Algorithmus etwas angepasst werden:
1 Setze $M := \varnothing$ 2 Finde den Knoten $V$ mit der geringsten Kardinalität 3 Wähle eine seiner Kante $e$, füge $e$ $M$ hinzu 4 Entferne $e$ und alle benachbarten Kanten aus $E$ 4 Falls $E \neq \varnothing$ gehe zu 2, sonst STOPP: $M$ ist maximal
Das Ergebnis ist ein perfektes Matching, wenn das möglich ist. Das Ergebnis ist ein perfektes Matching, wenn das möglich ist. Durch verbesserung der gierigen Erkennung des besten Kandidaten ist diese Herangehensweise zu einem Algorithmus geworden, der immer das beste Ergebnis liefert. Dies gelingt aber nicht für jedes Problem.
Die einfachste Greedy-Herangehensweise an das TSP ist die Nearest-Neighbor-Heuristik. Sie versagt spätestens dann, wenn die Dreiecksungleichung nicht gilt. Ist der Weg von einer Landeshauptstadt zur nächsten günstiger als der Weg zu einer Stadt in unmittelbarer Umgebung zur ersten Hauptstadt, werden erst alle Hauptstädte bereist und dan die anderen Städte, wobei gegen Ende der Abarbeitung sehr hohe Kosten entstehen können.
Greedy-Verfahren
Grundlegender Gedanke
Ein Verfahren, welches sich "Greedy" nennt, bearbeitet schrittweise ein Problem, indem es eine Teillösung ermittelt und diese kontinuierlich erweitert. Bei der Erweiterung der Teillösung wird typischerweise immer der am naheliegendste oder günstigste mögliche "Happen" gewählt, der noch nicht Bestandteil der Teillösung ist. Das Verfahren endet, wenn kein weiterer "Happen" vorhanden ist, um die Teillösung zu erweitern. Dann wird aus der Teillösung die Gesamtlösung.
Greedy-Heuristiken
- Heuristik
- Eine Heuristik (altgriech. εὑρίσκω, heurísko: "ich finde") ist ein analytisches Verfahren, bei dem Aussagen über ein System getroffen werden, die ausschließlich auf Vermutungen basieren.
Wie würde eine Greedy-Heuristik in der Graphentheorie aussehen?
Eine Greedy-Heuristik wäre ein simpler Ablaufplan, mit dem ein Problem in einem Graph schrittweise abgearbeitet wird. Dabei wird, wie charakteristisch für die Heuristik, immer eine Vermutung zugrunde gelegt, bei der davon ausgegangen wird, dass sie zur bestmöglichen Lösung führt.
- Ein beliebig gewählter Startpunkt (-knoten, -kante) wird der zunächst leeren Teillösung hinzugefügt.
- Von dort aus wird der nächste Problemteil (Knoten, Kante) gesucht, der am günstigsten erscheint und zur Teillösung hinzugefügt werden darf. -> Daraus folgt: heuristische Vermutung = günstigster "Happen" führt zur besten Lösung.
- Der neu hinzugefügte Problemteil ist der Ausgangspunkt, um Schritt 2 zu wiederholen, es sei denn, es kann kein Problemteil mehr der Teillösung hinzugefügt werden. In letzterem Fall endet die Heuristik, die gefundene Teillösung ist eine gültige Lösung für das zugrunde liegende Problem.
Welcher "Happen" der günstigste ist, ist vom zugrundeliegenden Problem und dem verwendeten Graphen abhängig. Beispiele:
- In einem Graphen mit bewerteten Elementen wird die kleinste/größte Bewertung gewählt, je nachdem, was vom Problem verlangt wird.
- In unbewerteten Graphen ist das nächste Element zufällig wählbar.
- In gerichteten Graphen können (bei Knotenproblemen) nur Knoten gewählt werden, die auch erreichbar sind.
Greedy-Algorithmen
Greedy-Algorithmen (gierige Algorithmen) zeichnen sich dadurch aus, dass sie schrittweise und ohne zurückzusetzen, eine Lösung aufbauen indem sie anhand lokaler Informationen den Folgezustand auswählen, welcher zum Zeitpunkt der Wahl das beste Ergebnis verspricht. Es werden dabei nicht mehr Teillösungen konstruiert als unbedingt nötig. Die Basis eines Greedy-Algorithmus ist eine bereits (absteigend) vorsortierte Liste. Wird diese erweitert, werden die entsprechenden Elemente direkt an die richtige Stelle einsortiert.
- Vorteil: meist schnell, liefert zumindest gute Lösungen
- Nachteil: keine Berücksichtigung früherer Lösungen, keine Revision einmal getroffener Entscheidungen, selten optimale Lösungen
Aufbau
Im Allgemeinen besteht ein Greedy-Algorithmus aus folgenden Bestandteilen:
- eine sich verbrauchende Kandidatenliste
- eine sich aufbauende Resultatliste
- Kontrollstrukturen
- loesung?, die kontrolliert, ob die aktuelle Resultatliste eine Lösung des Problems darstellt
- okay?, die kontrolliert, ob die Erweiterung einer Resultatliste durch den nächsten Kandidaten zulässig ist
- ziel, die den Wert einer Lösung angibt
- Auswahlfunktion
- naechster, die aus der Kandidatenliste den jeweils besten "Happen" auswählt
- Modifikationsfunktionen
- modify+, die die Kandidatenliste im positiven Fall, also wenn die Erweiterung zu einer zulässigen Liste führt, modifiziert
- modify-, die die Kandidatenliste im negativen Fall, also wenn die Erweiterung nicht zu einer zulässigen Liste führen würde, modifiziert
Matroide, Theorie der Unabhängigkeitsysteme
- Motivation: Ein Greedy-Algorithmus findet für ein Optimierungsproblem auf Unabhängigkeitssystemen genau dann die optimale Lösung, wenn die zulässigen Lösungen die unabhängigen Mengen eines Matroids sind. Sonst führt der Algorithmus lediglich zu einem lokalen Optimum. Ein Unabhängigskeitssystem ist umgekehrt genau dann ein Matroid, wenn ein Greedy-Algorithmus zu jeder Gewichtsfunktion immer Basen mit minimalen/maximalen Gewicht berechnen kann.
- Herkunft: Der Begriff Matroid bezeichnet eine Algebraische Struktur und entstammt der Untersuchung der Unabhängigkeit der Spaltenvektoren einer Matrix. Er ist eine Verschmelzung der Wörter "Matrix" und "Oides"(griech. ~ Ähnlichkeit).
- $\emptyset \in \mathcal{I}$ (Nicht zu verwechseln mit $\emptyset \subseteq \mathcal{I}$, was trivial wäre, da die leere Menge Teilmenge jeder Menge ist.)
- $A \subseteq B, B\in \mathcal{I} \Rightarrow A\in \mathcal{I}$ ($\mathcal{I}$ ist nach unten $\subseteq$-abgeschlossen.)
- Lineare Unabhängigkeit
In der linearen Algebra wird eine Familie von Vektoren eines Vektorraums linear unabhängig genannt, wenn sich der Nullvektor nur durch eine Linearkombination der Vektoren erzeugen lässt, in der alle Koeffizienten der Kombination auf den Wert null gesetzt werden. Äquivalent dazu ist, dass sich keiner der Vektoren als Linearkombination der anderen darstellen lässt. - Unabhängigkeit von ungerichteten Kanten
Die Kanten/Kantenkombinationen eines Graphen sind unabhängig solange sie keine Kreise enthalten. - Unabhängigkeit für Bipartites Matching
Die Elemente einer Menge in einem Matchingsystem sind Unabhängig wenn diese gleichzeitig gematcht werden können. - Unabhängigkeit von Gleichungen
Eine Menge von Gleichungen ist unabhängig wenn sich aus der Kombination dieser kein Ergebnis herleiten lässt. - Unabhängigkeit von gerichteten Kanten
??? - 1. $\emptyset \in \mathcal I$
- 2. $\forall A \in \mathcal I\, \forall B \in \mathcal P(E) \colon B \subseteq A \Rightarrow B \in \mathcal I$
- 3. $\forall A; B \in \mathcal I \colon \left| B \right| < \left| A\right| \Rightarrow (\exists x \in A \setminus B \colon B \cup \{x\} \in \mathcal I)$
- Für endlichdimensionale Vektorräume entspricht die Kardinalität der Basen der Anzahl der Dimensionen.
- Welcher Vektor ist nicht wie die Anderen?
- Welcher andere Vektor ist nicht wie die Anderen?
- Welches Vektorenpaar ist nicht wie die Anderen?
- A, immer wählbar ohne Abhängige Sets zu erzeugen
- F, da 0-Vektor, kein "Ortswechsel" mit ihm möglich
- DE, zeigen in die selbe Richtung / erfüllen den selben Zweck
- Welche Kante ist nicht wie die Anderen?
- Welche andere Kante ist nicht wie die Anderen?
- Welches Kantenpaar ist nicht wie die Anderen?
- A, da ohne ihn der Graph in 2 Teile zerfällt
- F, da kein "Ortswechsel" mit ihm möglich
- DE, haben die selbe Funktion(Zwillinge)
- Welcher Knoten ist nicht wie die Anderen?
- Welcher andere Knoten ist nicht wie die Anderen?
- Welches Knotenpaar ist nicht wie die Anderen?
- A, da er immer Wählbar ist
- F, da er niemals Wählbar ist
- DE, sind niemals gleichzeitig Wählbar
- $->$ Die jeweils letzte Zeile der Ergebnismengen sind die Basen = unabhängige Mengen, welche in ihrer Kardinalität nicht weiter wachsen können
- Handelt es sich bei den Ergebnismengen um ein Matroide?
- Ja. Es gibt zb. für jede Menge mit einer Kardinalität von 2 mindestens ein Element aus den Mengen mit einer Kardinalität von 3 welches noch hinzugefügt werden kann, sodass die Unabhängigkeit weiterhin besteht
- https://www.tu-chemnitz.de/mathematik/discrete/lehre/edm/w07/Algorithmen.pdf
- http://math.sfsu.edu/federico/Clase/Matroids/lectures.html
- https://de.wikipedia.org/wiki/Heuristik
- https://de.wikipedia.org/wiki/Matroid
- https://de.wikipedia.org/wiki/Greedy-Algorithmus
- Wagenknecht, Christian: Algorithmen und Komplexität, Carl Hanser Verlag GmbH & Co. KG, 1. Auflage (13. März 2003)
Ein Unabhängigkeitssystem ist in der Kombinatorik eine Verallgemeinerung der mathematische Struktur des Matroides.
Definition: Unabhängigkeitssystem
Sei $E$ eine beliebige endliche Grundmenge und $\mathcal I$ ein System von Teilmengen von $E$ (also $\mathcal I\subseteq \mathcal{P} (E)$ ), dann ist das Paar $(E,\mathcal{I})$ ein Unabhängigkeitssystem, wenn die folgenden Bedingungen erfüllt sind:
1. ist äquivalent zu der Forderung dass $\mathcal{I}$ nicht leer ist.
Durch Hinzufügen der sogenannten Austauscheigenschaft entsteht aus einem Unabhängigkeitssystem ein Matroid.
Definition: Matroid
Sei $E$ eine endliche Menge und $\mathcal I$ eine Teilmenge von $\mathcal P(E)$. Ein Matroid ist ein Paar $(E;\mathcal I)$ für welches folgende Bedingungen erfüllt sind:
Dabei ist $\left| A \right|$ die Kardinalität der Menge $A$.
Die Elemente von $E$ bilden die Grundmenge. Die Elemente von $\mathcal I$ bilden die unabhängigen Teilmengen, auch Set´s genannt, aus $E$.
Definition: Basis
Als Basis wird eine unabhängige Menge bezeichnet, welche in ihrer Kardinalität nicht weiter vergrößert werden kann.
Beispiele
1. Bilde die Menge der unabhägigen Vektoren! 
|
|||
2. Welche Kantenzüge sind unabhängig? 
|
|||
3. Bilde die Menge aller möglichen Matchings! 
|
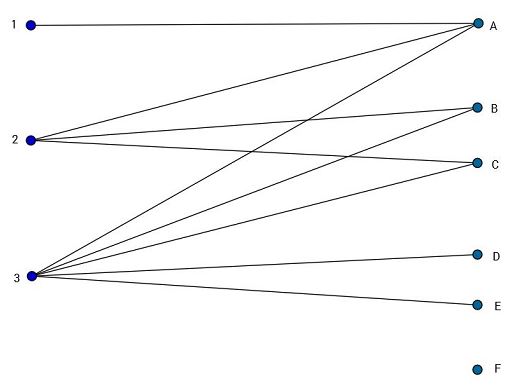
Aus den gegebenen Grundmengen $E$ = {a,b,c,d,e,f} lassen sich in den Beispielen folgende unabhängige Mengen bilden: Ergebnismenge für Beispiel 2 & 3 |
|
Die 3 Fragen, welche zu jeder Aufgabe gestellt wurden können auch gut genutzt werden um eine Bewertungsfunkton anhand dieser Merkmale zu erstellen. Somit wäre es zb. möglich in einem bipartiten Matching ein optimales Matching mit einem Greedyalgorithmus zu generieren, da nun eine Prioritätenliste existieren würde. |
