Färbungsprobleme
Aus ProgrammingWiki
Inhaltsverzeichnis |
Motivation
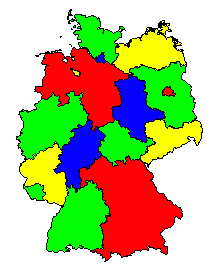
- Einfärben einer Karte mit so wenig Farben wie möglich, wobei zwei einander angrenzende Länder nie dieselbe Farbe haben dürfen
Färbungstheorie
Farbe
Ein Element $c$ heißt Farbe, wenn gilt: $c \in C$und $c$ ist von jedem beliebigen Element $c' \in C$unterscheidbar.
Aus mathematischer sowie programmiertechnischer Sicht ist es daher sinnvoll, Farben als Zahlen festzulegen. In graphischen Darstellungen sind hingegen tatsächliche Farben wesentlich geeigneter. Theoretisch jedoch ist alles als Farbe zugelassen.
Färbung
Eine Färbung ist ein Zuordnung einer Farbe zu Elementen eines Graphen. Eine Knotenfärbung zum Beispiel ordnet jedem Knoten eine Farbe zu. Insgesamt gibt es drei hauptsächliche Arten der Färbung eines Graphen:
- Knotenfärbung: jedem Knoten des Graphen wird eine Farbe zugeordnet
- Kantenfärbung: jeder Kante des Graphen wird eine Farbe zugeordnet
- Totalfärbung: sowohl jedem Knoten als auch jeder Kante wird eine Farbe zugeordnet
Im folgenden wird ausschließlich auf Knotenfärbung eingegangen. Definiert wird die Knotenfärbung (im folgenden nur Färbung) folgendermaßen:
Wenn $G(V,E)$ ein ungerichteter Graph ohne Schleifen und Mehrfachkanten ist, dann ist $f: V \to C$ die Färbung dieses Graphen.
Übung
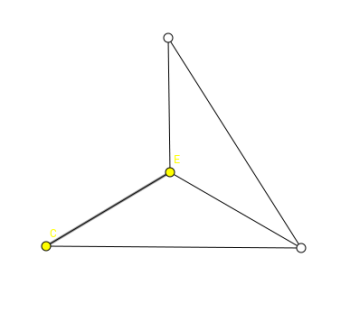
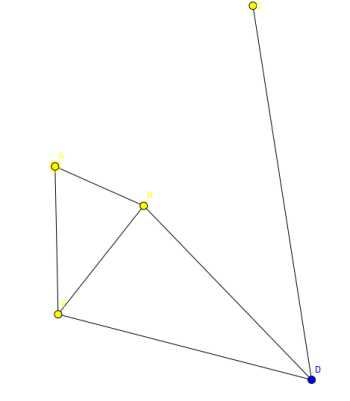
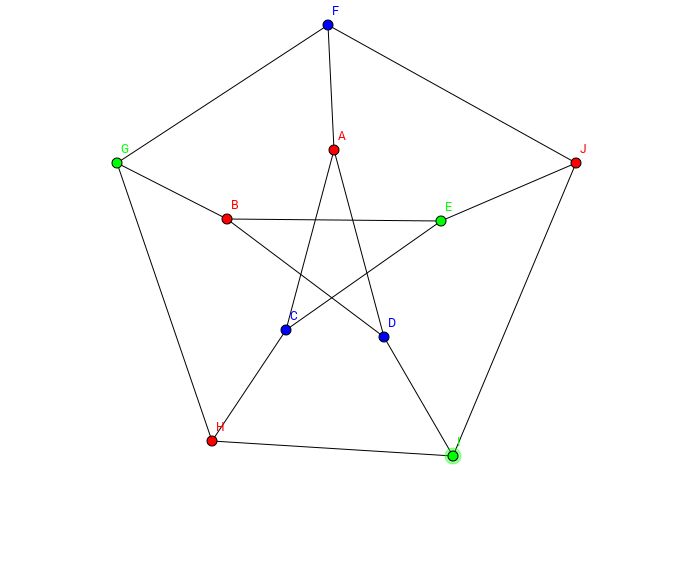
Sind die folgenden Graphen nach dieser Definition korrekt gefärbt?
Das Färben eines Graphen ist jedoch nicht beliebig möglich, wenn die Färbung gültig sein soll.
Wenn je zwei beliebige benachbarte Knoten nicht dieselbe Farbe haben, dann heißt die dazugehörige Färbung gültig. $\forall v \in V : \forall w \in \Gamma (v) : f(v) \ne f(w)$, wenn $\Gamma(v)$ die Menge aller Nachbarn von v bezeichnet.
Daraus ergibt sich auch die Notwendigkeit zu definieren, ob ich einen Graphen überhaupt gültig färben kann. Diese kann abgeleitet werden aus dem Wissen über die Gültigkeit einer Färbung.
Wenn es eine gültige Färbung $f$ gibt, die eine Anzahl $k$ an Farben verwendet, dann heißt der so gefärbte Graph $G$ k-färbbar.
Übung
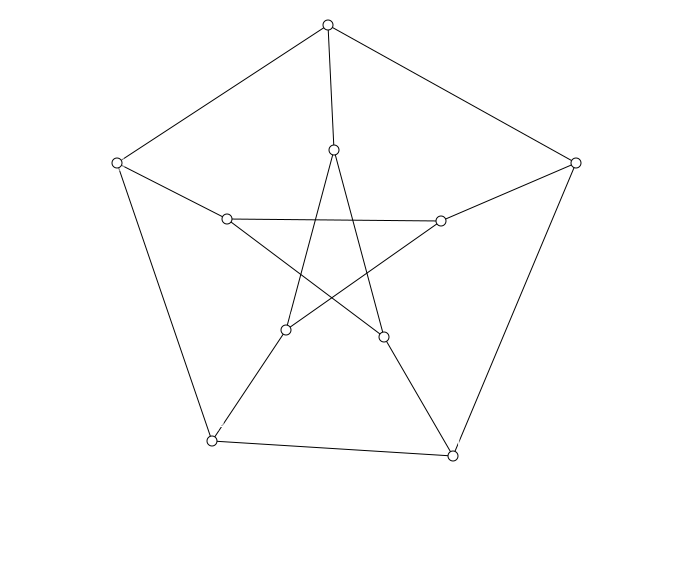
Finden sie eine gültige Färbung für den nachstehenden Graphen. Schätzen sie auch, wie viele Farben sie mindestens brauchen werden.
Greedy-Algorithmus zum Färben eines Graphen
Um einen Graphen $G$ effizient gültig einzufärben, genügt ein "gieriger" Algorithmus. Dieser wird stets eine gültige Färbung zurückgeben, garantiert jedoch nicht, dass die Färbung mit der geringstmöglichen Anzahl an Farben auskommt. Im Algorithmus wird der Begriff der "nächsten" Farbe verwendet. Damit ist gemeint, dass den Farben ein numerischer Index gegeben werden soll. Die "nächste" Farbe ist die Farbe mit dem geringsten Index (innerhalb der gegebenen Einschränkungen).
- 0. Wähle einen beliebigen Startknoten. Dieser ist der erste aktive Knoten.
- 1. Prüfe alle Nachbarknoten des aktiven Knoten, ob sie gefärbt sind. Wenn ja, streiche für jeden gefärbten Knoten dessen Farbe aus der Liste der erlaubten Farben. Füge jeden ungefärbten Knoten der Nachbarschaftsliste $NL$ hinzu, außer er ist bereits enthalten.
- 2. Färbe den aktiven Knoten mit der nächsten Farbe aus der Liste der erlaubten Farben.
- 3. Entferne den gefärbten Knoten aus der Liste der Nachbarschaftsknoten. Ist die Nachbarschaftsliste leer, gib die Färbung zurück. Wenn nicht, setze den ersten Knoten aus der Nachbarschaftsliste als den nächsten aktiven Knoten und wiederhole dann Schritt 1.
Theoretische Laufzeitanalyse
In einer Worst-Case-Betrachtung liegt ein vollständiger Graph vor, d.h. ein Graph, in dem jeder Knoten mit jedem anderen verbunden ist. Da jeder Knoten einmal aktiver Knoten ist, müssen alle Knoten einmal durchlaufen werden. Daraus resultiert eine Mindestlaufzeit von $O(n)$. In jedem dieser Schritte müssen nun alle Nachbarknoten geprüft werden, entweder auf seine Farbe, damit der aktive Knoten nicht falsch gefärbt wird, oder, wenn er keine Farbe hat, um ihn dann der Nachbarschaftsliste hinzuzufügen. Im schlechtesten Fall, also in einem vollständigen Graphen, sind das $n-1$ Knoten, da der zu färbende Knoten nicht mitgezählt wird. Damit beträgt die Laufzeit im Worst Case mindestens $O(n * (n-1))$, also $O(n^2 - n)$, was auf $O(n^2)$ gekürzt werden darf.
Darüber hinaus können Operationen wie das Entfernen des ersten Elements aus der Nachbarschaftsliste ebenfalls aufwändiger als $O(1)$ sein, dies ist jedoch implementierungsabhängig und daher nicht konkreter Inhalt dieser Betrachtung.
Die chromatische Zahl
Für Anwendungsfälle sollten Färbungen mit möglichst wenig Farben auskommen. Die Mindestanzahl an benötigten Farben heißt chromatische Zahl.
Die chromatische Zahl $\chi (G)$ ist die kleinste natürliche Zahl, für die der Graph $G$ eine gültige Färbung mit ebensovielen Farben besitzt. Gibt es für keine Anzahl an Farben eine gültige Färbung, so ist $\chi (G) = \infty$
Die höchste Anzahl an benötigten Farben, um einen beliebigen, schleifenfreien Graphen einzufärben, entspricht der Anzahl der vorhandenen Knoten. Die Problem der Bestimmung der chromatischen Zahl für einen beliebigen Graphen ist wahrscheinlich nicht effizient zu lösen.
Spezialfälle
- Wenn der Graph keine Kanten enthält, dann ist die chromatische Zahl 1, da alle Knoten disjunkt sind und daher mit derselben Farbe eingefärbt werden können
- Die chromatische Zahl beträgt 2, wenn der Graph bipartit ist. Das liegt daran, dass alle Knoten in jeder der beiden Knotenmengen (Partitionen) dieselbe Farbe bekommen können.
- Für planare bzw. plättbare Graphen gilt, dass die höchstmögliche chromatische Zahl 4 ist. Dies ist bekannt als der Vier-Farben-Satz.
Allgemein gilt: Die Frage nach der chromatischen Zahl eines Graphen ist äquivalent zu der Frage, für welches k der Graph k-partit ist.
Das chromatische Polynom
Das chromatische Polynom gibt an, wieviele Färbungen eines Graphen es für eine gegebene Menge an Farben gibt.
Das chromatische Polynom $\chi (G,k)$ ist eine Formel, die die Menge an gültigen Färbungen des Graphen $G$ mit $k$ Farben berechnet.
Die chromatische Zahl ist das kleinste $k$, für dass das chromatische Polynom einen Wert $\ne$ 0 liefert.
Das chromatische Polynom ist nicht in polynomieller Laufzeit ermittelbar, ähnlich wie die chromatische Zahl.
Beide sind sogenannte NP-vollständige Probleme.
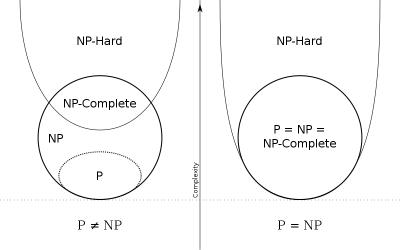
NP-schwere und NP-vollständige Probleme
Um zu verstehen, was ein NP-vollständiges Problem ist, muss man zuerst den Begriff der NP-Schwere definieren.
Ein Problem $p$ heißt NP-schwer, wenn es sich in polynomieller Laufzeit mittels eines deterministischen Verfahrens auf ein Problem $q$ aus der Komplexitätsklasse $NP$ reduzieren lässt.
Das heißt, ein solches Problem $p$ ist "schwerer" als das Problem $q$. Die Definition für ein NP-vollständiges Problem ist nun eine Verschärfung der obigen Definition.
Ein Problem $p$ heißt NP-vollständig, wenn es sich um ein NP-schweres Problem handelt und es Element der Komplexitätsklasse $NP$ ist.
Die Bestimmung der chromatischen Zahl und des chromatischen Polynoms sind deswegen NP-vollständig, da gezeigt wurde, dass sie sich auf das Entscheidungsproblem der Aussagenlogik, kurz SAT, reduzieren lassen. Von diesem ist sicher bekannt, dass es ebenso NP-vollständig ist. Analog dazu gilt natürlich auch, dass die Bestimmung des kleinsten $k$, für das ein Graph k-partit ist für $k \ge 3$, ein NP-vollständiges Problem ist.
Anwendungen
Es existieren eine Reihe durchaus praxisrelevanter Anwendungsfälle, die aufgrund der Färbungstheorie nicht effizient mit Computern gelöst werden können.
- farbeffiziente Färbung von Landkarten
- Aufbau von Segmenten in RAID-Systemen
- Scheduling-Probleme (Stunden- bzw. Raumpläne, Terminkorrelation)