Euler-Kreise und -Wege Übung
Aus ProgrammingWiki
Inhaltsverzeichnis |
Aufgabe 1 - Unterscheidung der Graphen
Unterscheiden Sie die Graphen nach eulersch, semi-eulersch oder weder noch.
a)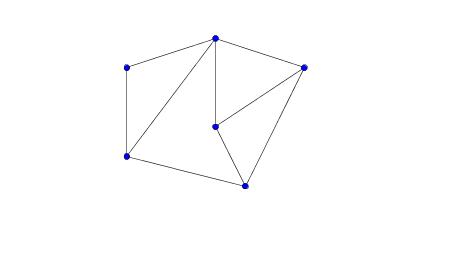
b)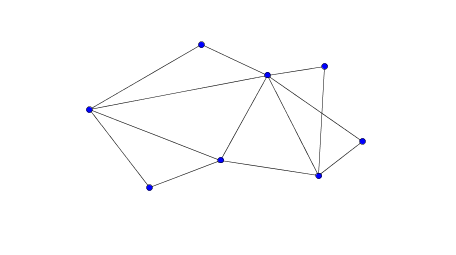
c)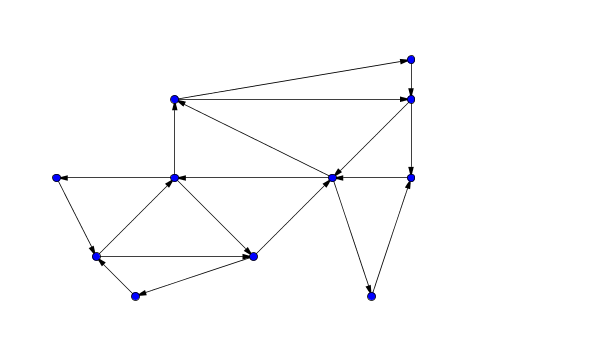
d)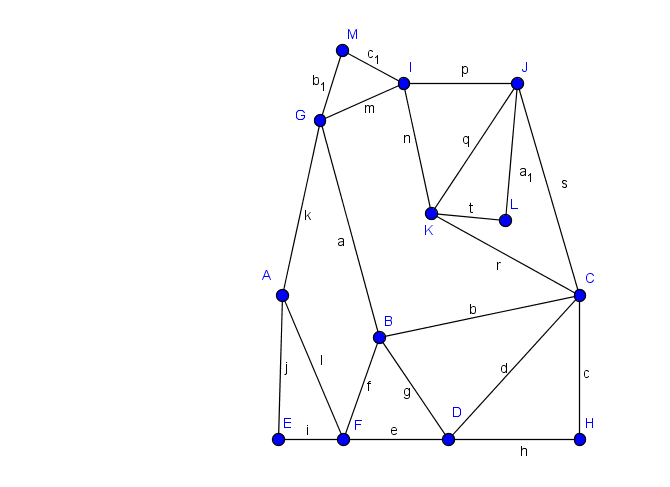
e)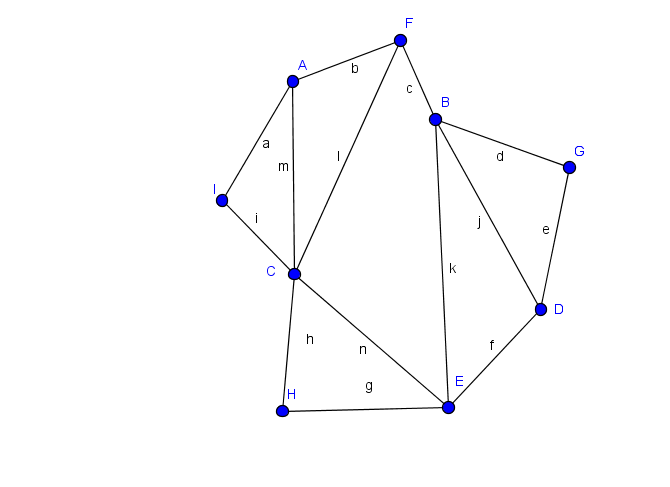
Aufgabe 2 - Worträtsel
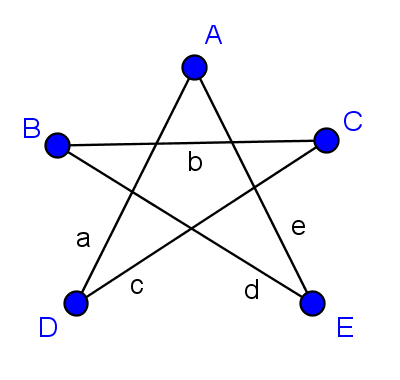
Bilden Sie einen Euler-Weg, der vom rotmarkierten Punkt beginnt ,sodass die abgelaufenen Kanten eine Lösungswortgruppe ergeben.
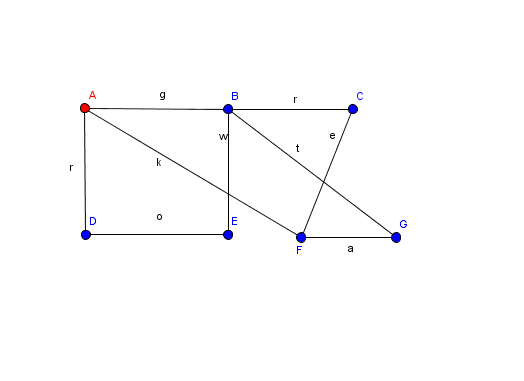
Aufgabe 3 - Algorithmus
Wenden Sie einen der beiden in der Vorlesung behandelten Algorithmen zum Nachweisen der Eulerschkeit eines Graphen(Hierholzer/Fleury) an.
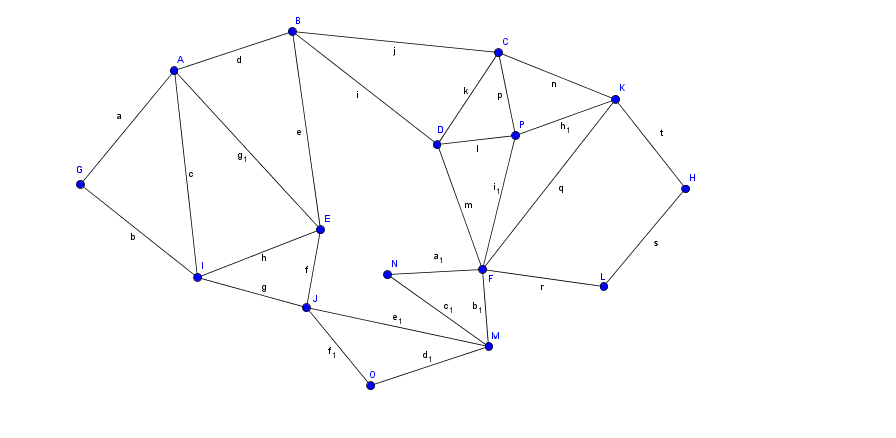
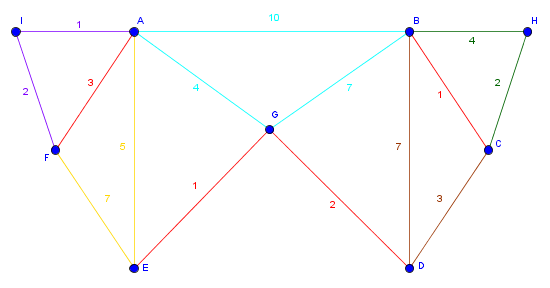
Aufgabe 4 - Postbotenproblem
Wenden Sie den Postbotenalgorithmus für folgenden Graphen an.
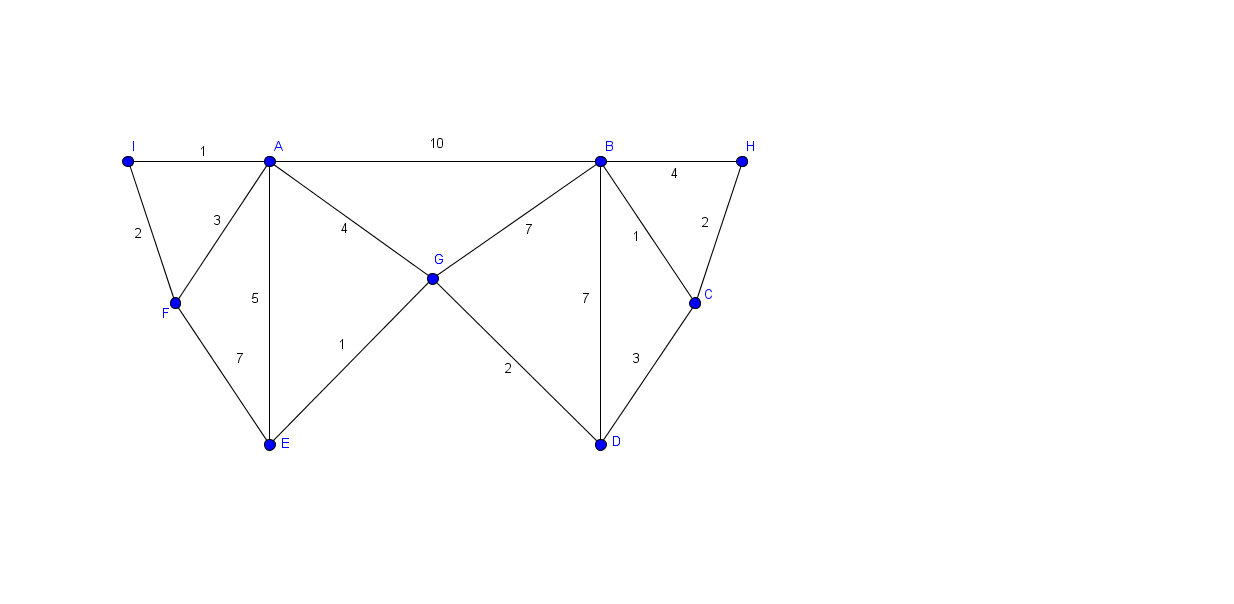
Aufgabe 5 - Empirische Analyse
Führen Sie eine empirische Analyse durch
Aufgabe 6 - Zeichnen
Zeichnen Sie mindestens 3 Graphen mit 5 Knoten die einen Eulerkreis beinhalten.
Lösungen
Aufgabe 1: a) nicht eulersch b) eulersch c) semi-eulersch d) eulersch e) nicht eulersch
Aufgabe 2: Lösungswort: great work
Aufgabe 3:
Eine von vielen möglichen Lösungen des Hierholzer Algorithmuses:
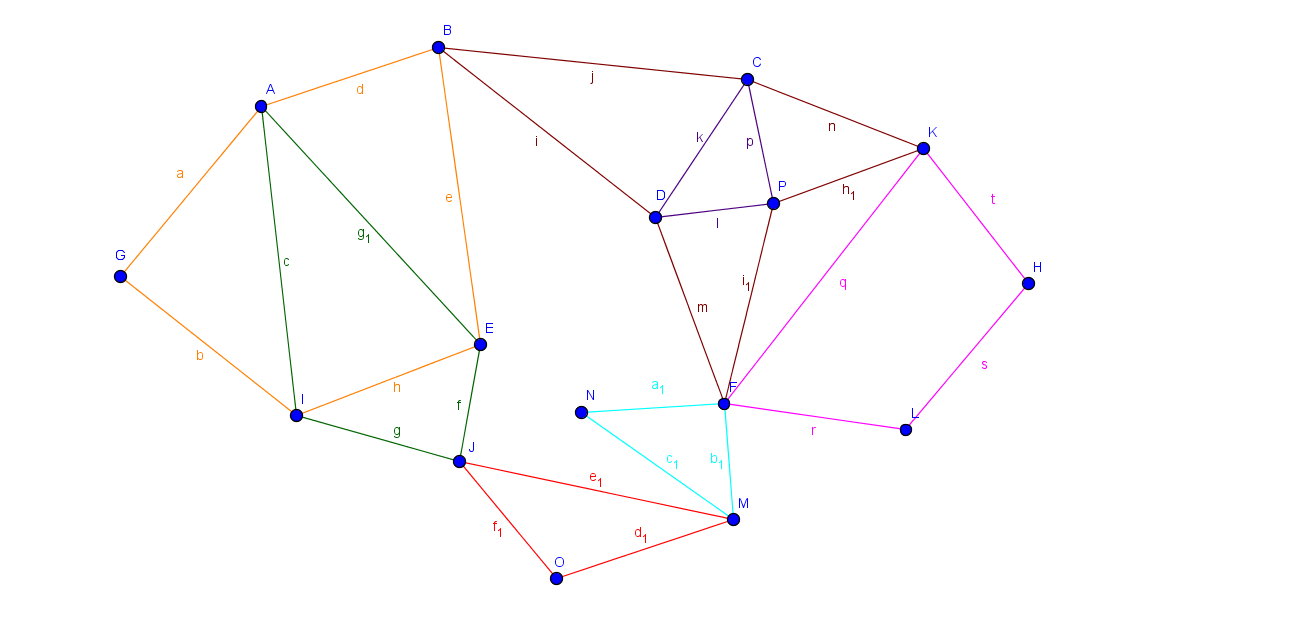
Und die Lösung mit dem Agorithmus von Fleury:
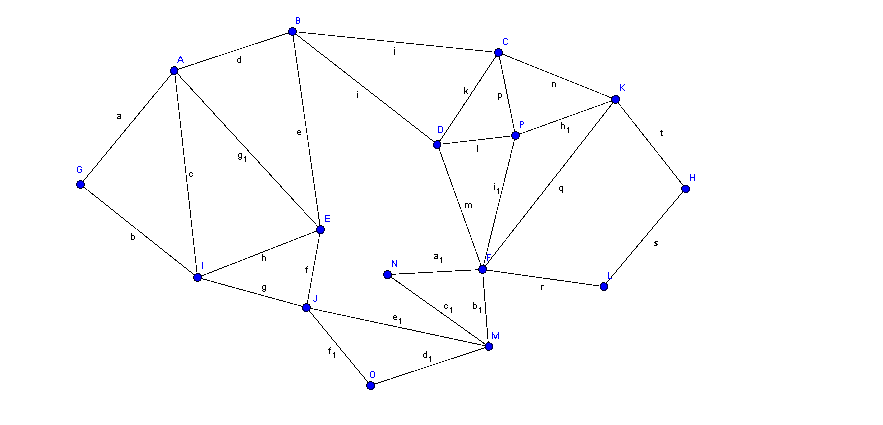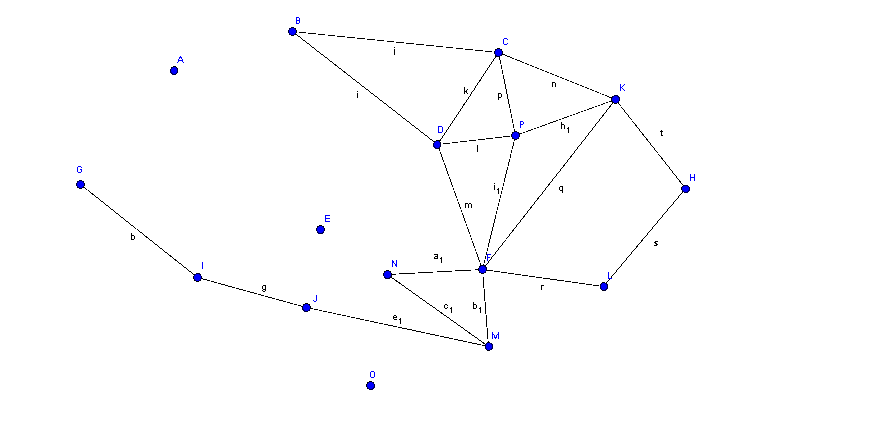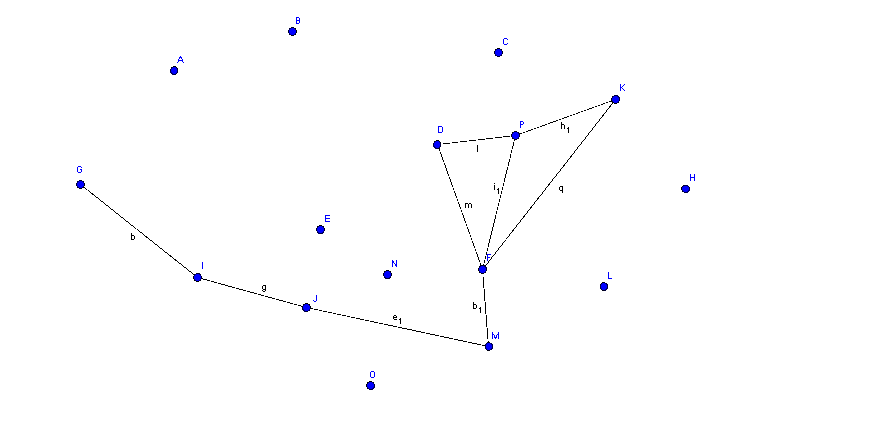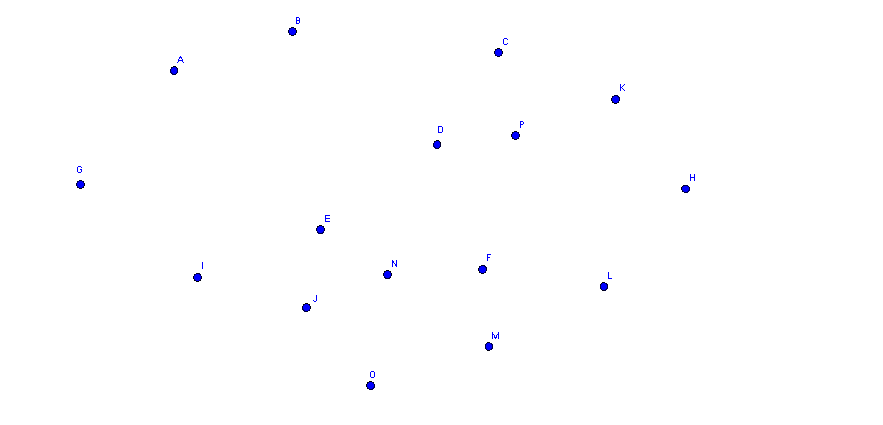
Aufgabe 4:
Der vollständige Graph G' aus allen Knoten mit ungeraden Grad, die kürzesten Wege zwischen diesen sowie eingefügten Matchingkanten:
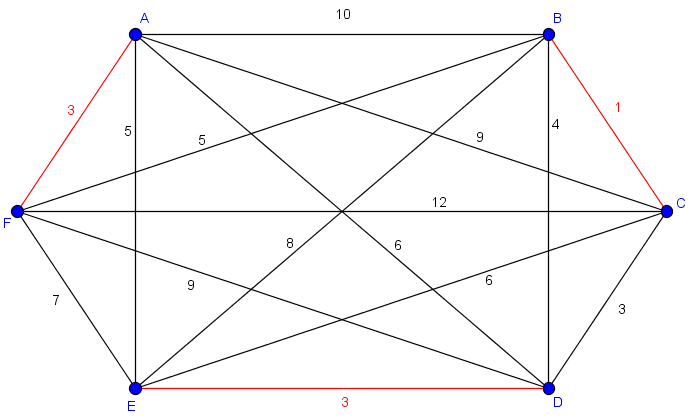
Die Integrierung in den Graphen G (rot = doppelte Kante):
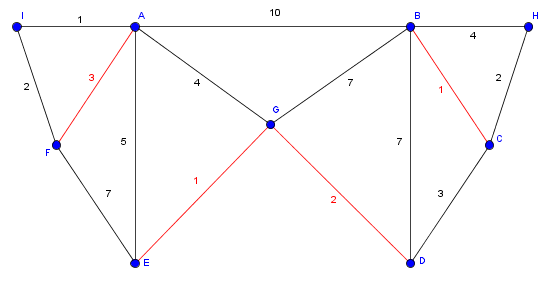
Anwendung des Hierholzer Algorithmus:
Aufgabe 6:
3 von vielen Möglichkeiten:
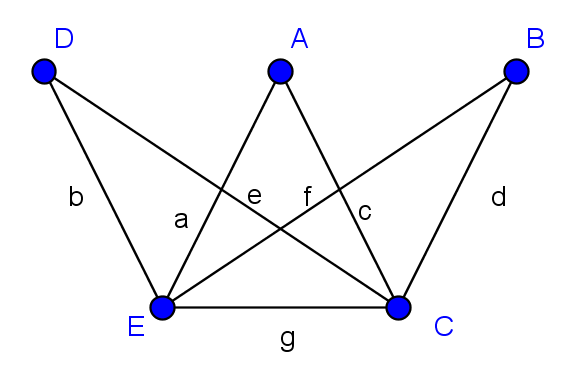
1. 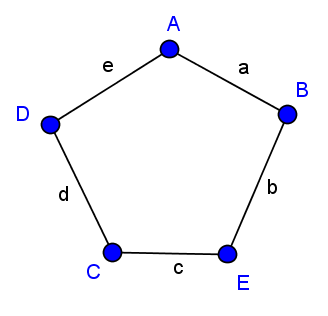 2.
2. 
3.