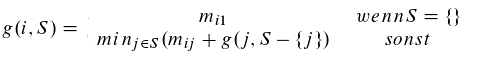Dynamisches Programmieren WS15-16

Aus ProgrammingWiki

Wechseln zu: Navigation, Suche

Leonard Mory, Frank Ehrlich, Alexander Preuss

Inhaltsverzeichnis

Thematischer Einstieg und Motivation

Was ist dynamisches Programmieren?

  • Kein Algorithmus, eher eine Lösungsstrategie
  • Begriff kommt aus der Zeit, wo Programmieren Tabellenmethoden bezeichnete
  • Optimierungsverfahren, kein Programmieren
  • "Teile und Herrsche" dient als Grundlage

Vorgehensweise

  1. Darstellung der Struktur einer optimalen Lösung.
  2. Entwerfen einer rekursiven Methode, um den Wert der optimalen Lösung zu bestimmen.
  3. Berechnung des Wertes einer optimalen Lösung durch eine iterative Bottom-Up-Methode.
  4. Bestimmung einer optimalen Lösung aus den bereits berechneten Daten.

Dabei könnnen aber immer Schwierigkeiten auftreten:

  • Lösungen kleiner Probleme können nicht immer so kombiniert werden, dass sich eine optimale Lösung für ein größeres Problem ergibt
  • Menge der zu lösenden Teilproblemen kann unlösbar hoch werden
  • Aufspaltung in eigenständige Teilprobleme ist oft nicht möglich

Bottom-up

Bei dem Dynamischen Programmieren wird ein Bottom-up-Ansatz verwendet

  • Um ein umfangreiches Problem zu lösen, wird es in kleine Teilprobleme zerlegt
  • Alle Teillösungen werden unabhängig von einander "von unten her" gelöst und in eine Tabelle gespeichert
  • Durch die Speicherung in die Tabellen wird eine neue Berechnung vermieden
  • Erwartung, dass eine optimale Lösung aus allen Teillösungen entsteht
    • Lösung kann aber nicht immer als optimale Lösung betrachtet werden, da verschiedene Lösungen möglich sind mit dem optimalen Wert
  • Berechnungsprozess wird iterativ abgewickelt

Berechnungsprozess

  • wird iterativ organisiert
    • das heißt, dass die entsprechende Tabelle nacheinander ausgefüllt wird
  • für jedes Feld einer Tabelle oder einer Matrix mit der Form (z,s )muss genau ein Resultat ermittelt werden
    • diese Berechnungsmethode könnte sozusagen aus Aufwandsgründen der rekursiven vorgezogen werden
Bei Lösungen, welche rekursiv definiert sind und durch rekursive Prozeduren berechnet wurden, können Mehrfachberechnungen von Teilausdrücken vorkommen.

Erklaerung fib.PNG

  • Aufwand für wiederholte und damit hinfällige Berechnungen wird bei der dynamischen Programmierung vermieden
    • das geht aber nicht so einfach, man spricht von so genannten "überlappenden Teilproblemen"
  • um das zu bewirken werden alle Teillösungen berechnet
    • auch die, welche für die optimale Gesamtlösung am Schluss unrelevant sind und somit eigentlich keine Bedeutung haben
  • schwieriger ist es, den Top-Down-Ansatz in einen Bottom-Up-Algoritmus umzuformen
    • Bottom-Up-Algorithmen durchlaufen zweidimensionale Tabellen mittels verschachtelter Schleifen
    • daher kann die Umwandlung schwierig sein und einen hohen mentalen Zeitaufwand mit sich bringen
    • zudem ist sie dadurch sehr fehleranfällig
Durch "Memorizing" kann man diesem Problem aus dem Weg gehen. Die Idee besteht darin, rekursiv erzeugte Teilprobleme einmal zu berechnen und in eine Tabelle zu speichern. Vor jeder Berechnung wird dann geprüft, ob der Wert schon vorhanden ist. Wenn das der Fall ist, wird der Wert übernommen, ansonsten wird er berechnet und danach in die Tabelle eingetragen.

Dynamisches Programmieren vs Memoizing

  • beide vermeiden wiederholte Berechnung durch Speichern
    • ⇒Tradeoff: Speicher statt Zeit
Memoization Dynamisches Programmieren
Top-Down, Depth-First Ansatz Bottom-Up, Breadth-First Ansatz
Beschreibung bleibt unverändert Beschriebung wird verändert
Vermeidet unnötige Berechnungen Kann unnötige Berechnungen nicht vermeiden
Kann Speicher leicht verschwenden Kann Speicher einsparen, indem unnötige Resultate vermieden werden
Muss prüfen ob Berechnung bereits vorliegt keine Prüfung nötig durch neue Beschreibung
Komplexität hängt von Schnelligkeit des "Nachschlagens" ab Komplexität hängt von Speichermethode ab



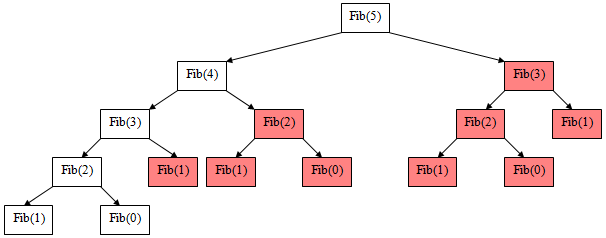
Vergleich anhand Fibonacciberechnung

Rekursive Berechnung, naiver Ansatz

Rekursive Berechnung mit Memoizing

Berechnung mit dynamischem Programmieren

Schritte zum Algorithmus mit dynamischer Programmierung

 1. Struktur einer optimalen Lösung analysieren:
    Problem zerlegen, Teilprobleme formulieren
 2. Rekursionsgleichung für die optimale Lösung suchen
 3. Rekursive Lösung mit Memoizing formulieren
 4. (Umwandlung in Bottom-Up-Ansatz)
 5. Lösungswege aus Berechnungen konstruieren
 
 Problem: Bottom-Up Ansatz kann schwer zu finden sein

Bierproblem

mini

Informatikertreffen → Fachdiskussion

Problemstellung:

  • Wieviele Möglichkeiten gibt es 3 Flaschen Bier dem Sixpack zu entnehmen?
    • Wie löst man das als Informatiker?
  • Mathematik: Binomialkoeffizient
  • ${n \choose k} = \frac{n!}{(n-k)! k!}$ also ${6 \choose 3} = \frac{6!}{(6-3)! 3!}$
  • Rekursion!
    • ${n \choose k} = {n-1 \choose k-1} + {n-1 \choose k}$
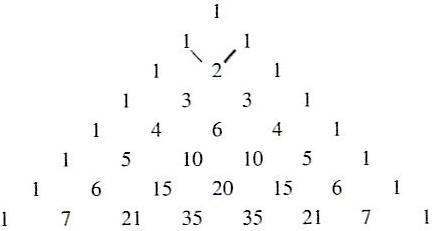
  • Pascalsches Dreieck

mini

  • Ergebnis in Zeile[n+1], Spalte [k]
    • Antwort: es gibt 20 Möglichkeiten (Zeile 7, Spalte 3)
  • Wir können das Problem mit einer Dreiecksmatrix lösen
    • Wir berechnen unnötige Werte
    • Für $Wert[i][j]$ werden nur $Wert[i-1]j-1]$ und $Wert[i-1][j]$ benötigt
    • Alle Werte mit $j>n$ werden nicht benötigt, Matrix braucht in jeder Zeile nur bis Spalte $n$ ausgefüllt werden


Rucksackproblem

  • ein Rucksack soll so gefüllt werden, dass die Wertsumme der eingepackten Gegenstände unter Beachtung seiner Kapazitätsschranke maximal ist
  • 0/1 Rucksackproblem: jeder Gegenstand wird entweder vollständig in den Rucksack aufgenommen (1) oder nicht eingepackt (0)


Iterative Berechnung

Instanz eines 0/1-Rucksackproblems mit K = 5

$i$ 1 2 3 4
$g_i$ 2 3 4 5
$w_i$ 3 7 2 9


Lösung

  • eine Zeile 0 für den Anfangs leeren Rucksack
  • Spaltenköpfe für alle möglichen Gewichtsumen von 0 bis K
  • bei Gegenstand 1 darf nur dieser in betracht gezogen werden
  • bei Gegenstand 2 darf der 2. und der 1. Gegenstand in betracht gezogen werden
  • bei Gegenstand 3 alle 3
  • bei Gegenstand 4 alle


$n/K$ $0$ $1$ $2$ $3$ $4$ $5$
$0$ 0 0 0 0 0 0
$1:(g_i=2; w_i=3)$ 0 0 3 3 3 3
$2:(g_i=3; w_i=7)$ 0 0 3 7 7 10
$3:(g_i=4; w_i=2)$ 0 0 3 7 7 10
$4:(g_i=5; w_i=9)$ 0 0 3 7 7 10


Berechnung zur Tabelle

Jeder Gegenstand darf nur einmal in den Rucksack

Gegenstand 0:

  • für den Anfangs leeren Rucksack

Gegenstand 1:

  • nur der 1. Gegenstand darf in den Rucksack -> daher 0 oder 3

Gegenstand 2:

  • (Zeile:Spalte) 2:2 -> Wert 3, da der 1. Gegenstand Wert 3 hat;
  • 2:3 -> Wert 7, da der 2. Gegenstand Wert 7 hat;
  • 2:4 -> Wert 7, da 4 kg - 3 kg = 1 kg (Verlust)-> ich gucke bei 1:1 -> Wert 0 -> 7 + 0 = 7
  • 2:5 -> Wert 10, 3 kg hat den Wert 7, 5 kg - 3 kg = 2 kg den Wert 3 in 1:2

Gegenstand 3:

  • fängt bei 4 kg an -> vorige Werte können daher übernommen werden
  • 3:4 -> Wert wäre 2, aber 2 < darüberliegende Wert 7 -> daher wird 7 genommen
  • 3:5 -> g3 Wert 2, 5 kg - 4 kg = 1 kg Verlust -> bei 2:1 Wert 0 -> 2 + 0 = 2 -> 2 < 10 -> geht nicht -> Wert 10 eintragen

Gegenstand 4:

  • fängt bei 5 kg an -> vorige Werte können daher übernommen werden
  • 4:5 -> Wert wäre 9, aber 9 < darüber liegende Wert 10 -> Wert 10 wird eingetragen

Der folgende Code berechnet iterativ den gesuchten Maximalwert aus 10 Gegenständen.

Dieser Code kann hier nicht ausgeführt werden! Daher laden Sie sich bitte das kostenlose Tool "DrRacket" (https://download.racket-lang.org/) herunter, wählen die Sprache "#lang racket", fügen den unten stehen Code in das Definitionsfenster ein, betätigen oben rechts "Start", geben im Iterationsfenster "(gesamtwert-iterativ 10 120)" ein und betätigen "Start" erneut.

Rekursive Berechnung ohne Memoizing

Bottom-up-Ansatz: Die optimale Gesamtlösung wird durch optimalen Teillösungen aufgebaut. Dies gilt aufgrund folgender Überlegungen: Gegenstand $i$ wird in den optimal gepackten Rucksack (zunächst noch ohne $i$) gesteckt. Für den Gesamtwert $wert (n,K)$ des Rucksacks gilt folgende rekursive Beziehung:

$i=\text{ Gegenstand }$

$g=\text{ Gewicht }$

$w=\text{ Wert des Gegenstands }$

$n = \text { Anzahl der Gegenstände }$

$K = \text{ Kapazität des Rucksacks }$

$wert(i,g) = \text{ Optimaler Wert für die Gegenstände }$

$wert(n,K)=\text{ Optimaler Gesamtwert }$


$wert(i,g) = \begin{cases} 0, & wenn \ i =0 \\ wert(i-1, g), & wenn \ i > 0 \ und \ g-g_{i} < 0\\ max(wert(i-1,g), wert(i-1, g-g_{i})+w_{i}), & sonst \\ \end{cases}$


$wert (n,K)$ bezeichnet den größtmöglichen Wert des Rucksackinhalts, wobei anfangs die volle Restkapazität $K$ zur Verfügung steht. Die Gegenstände werden mit 1,2,...,n durchnummeriert. Der Fall $wert(i,g) = wert(i-1,g)$ beschreibt, dass der $i$-te Gegenstand nicht in den Rucksack gepackt wird. $wert(i-1,g)$ ist der durch Aufnahme von Gegenständen aus 1,2,...,$i$-1 erziehlte Maximalwert unter Berücksichtigung der gegebenen Kapazität. Es gibt keinen Wertzuwachs, wenn Gegenstand $i$ nicht eingepackt wird. Der dritte Fall in der Definition von $wert$ beschreibt die Aufnahme von $i$, wonach eine Restkapazität von $g-g_{i}$ verbleibt. Der Gesamtwert steigt in diesem Fall um $w_{i}$. Es ist aber nicht ausgeschlossen, dass sich ein höherer Gesamtwert einstellt, wenn man den Gegenstand $i$ nicht in den Rucksack packt. Deshalb ist die in der Definition angegebene Maximumbestimmung aus $wert(i-1, g)$ und $wert(i-1, g-g_{i})+w_{i})$ erforderlich.

Eine direkte Implementation dieser Formel erledigt die folgende rekursive Prozedur (zunächst) ohne memoizing). Es wird dafür gesorgt, dass die Anzahl der rekursiven Aufrufe ermittelt wird. Um die rekursive Prozedur mit memoizing zu implementieren, benötigt es nur wenige Änderungen im bereits vorhandenen Quellcode.

Damit dieser Code ausgeführt werden kann, benutzen Sie bitte "DrRacket" (siehe oben).

  • das Ergebnis ist wie bei der iterativen Berechnung ebenfalls 183
  • die Anzahl der rekursiven Aufrufe bestimmt die Zahl der zu lösenden Teilprobleme
  • Deren Bearbeitungsreihenfolge wird durch den rekursiven Prozess bestimmt
  • Anzahl der rekursiven Aufrufe: 2026 > bei Iterativ: 1200 (10 * 120)
  • -> einige Tabellenwerte werden mehrfach berechnet
  • Lösung des Problems: memoizing

Rekursive Berechnung mit Memoizing

  • bevor eine Berechnung durchgeführt wird, wird überprüft, ob dieser Wert bereits existiert; wenn ja, dann wird dieser genommen; wenn nein, dann wird dieser berechnet und gespeichert

Um die rekursive Prozedur mit memoizing zu implementieren, benötigt es nur wenige Änderungen im bereits vorhandenen Quellcode. Damit dieser Code ausgeführt werden kann, benutzen Sie bitte "DrRacket" (siehe oben).


Aus dem Aufrufbeispiel

> (gesamtwert-rekursiv-memo 10 120)

'(183 502 501)

wird einiges deutlich:

  • Das Ergebnis (183) stimmt mit den Resultaten überein, die von gesamtwert-iterativ und gesamtwert-rekursiv ermittelt wurden.
  • Zahl der rekursiven Aufrufe 502 < 2026 (rekursive Berechnung ohne memoizing) und < 1200 bei iterativen Verfahren). Es werden nicht alle Tabelleninhalte gebraucht und mit der rekursiven Prozedur (mit und ohnememoizing) auch nicht berechnet.
  • Die Länge (501) von memoliste stimmt (beinahe) mit der Anzahl der rekursiver Aufrufe überein. Der erste kommt hinzu und sorgt für die Zahl 502.

Fazit

  • bei einer geringen Anzahl an Gegenständen, wie hier dargestellt, ist der unterschied zwischen den Lösungsansätzen nicht signifikant
  • die rekursive Berechnung ohne memoizing ist untauglich, da unnötige Mehrfachberechnung
  • die memoizing- Methode ist mindestens so schnell wie die iterative Methode geben, ermöglicht eine direkte Ableitung der rekursiven Regeln und vermeidet die fehleranfällige Transformation in einen iterativen Bottom-up-Algorithmus -> rekursive Berechnung mit memoizing ist die beste Wahl

Rundreiseproblem

Gegeben
  • $n$ Städte, Entfernungsmatrix $M=(m_{ ij }), m_{ ij }$
    • Entfernung von Stadt $i$ nach Stadt $j$
Gesucht
  • Rundreise über alle Städte mit minimaler Länge, also Permutation $π = \{1,...,n\} \rightarrow \{1,...,n\}$ sodass $c(p)=\sum\limits_{ i=1 }^{ n-1 } m_{ \pi(i), \pi(i+1) } + m_{ \pi(n), \pi(1) }$ minimal ist
Nun aus der Sicht der dynamischen Programmierung
  • Es sei $g(i,S)$ die Länge des kürzesten Weges von $i$ über jede Stadt in $S$ mit genau einem Besuch
Lösung des TSP $g(1,\{ 2,...,n \} )$
  • Stadt 1 kann nach Belieben gewählt werden da eine Rundreise gesucht wird
Es gilt

Tsp formel.PNG

Algorithmus

   1 $for (i=2; i=n; i++)  g[i,{}]= m_{i1}$
   2 $for (k=1; k=n-2; k++)$
   3   $for(S, |S|=k, 1 \notin S)$
   4     $for(i \in \{2,...,n\} -S)$
   5       $Berechne g[i, S] gemäß der Formel$
   6 $Berechne g[1,\{1,...,n\}] gemäß der Formel$
Komplexität der Tabelle
  • Tabellengröße mal den Aufwand des Tabelleneintrages
Anzahl der Tabellenfelder
  • $<n \cdot 2^{n-1}$
    • Anzahl der i's mal der Anzahl der betrachteten Teilmengen
Tabelleneintrag
  • Suche nach dem Minimum unter $j$ aus $S: \mathcal{O}\left(n\right)$
Laufzeit
  • $\mathcal{O}\left(n^{2}2^{n}\right)$, läuft deutlich besser als der naive Algorithmus mit der Laufzeit$(n-1)!$

Beispiel

Vier Städte mit deren Entfernung
01 02 03 04
01 - 4 9 8
02 4 - 12 2
03 9 12 - 10
04 8 2 10 -
Tabelleneinträge

$g[2,{}]=4$
$g[3,{}]=9$
$g[4,{}]=8$

$g[2,\{3\}]=12+9=21$
$g[2,\{4\}]=2+8=10$
$g[3,\{2\}]=12+4=16$
$g[3,\{4\}]=10+9=19$
$g[4,\{2\}]=2+4=6$
$g[4,\{3\}]=10+9=19$

$g[2,\{3,4\}]=min(m_{23}+g[3,\{4\}], m_{24}+g[4,\{3\}])=21$
$g[3,\{2,4\}]=min(m_{32}+g[2,\{4\}], m_{34}+g[4,\{2\}])=16$
$g[4,\{2,3\}]=min(m_{42}+g[2,\{3\}], m_{43}+g[3,\{2\}])=23$

$g[1,\{2,3,4\}]=min(m_{12}+g[2,\{3,4\}], m_{13}+g[3,\{2,4\}], m_{14}+g[4,\{2,3\}])=25$

Per Hand dieses Problem zu lösen ist sehr verwirrend und nach einer Weile wird man die Existenz korrekter Programme schätzen.
Die Lösung ist
1, 2, 4, 3, 1

Anwendung

Berechnung der Levenshtein Distanz (Unterschiede zwischen zwei Sätzen)

Quellen

Von „https://programmingwiki.de/Dynamisches_Programmieren_WS15-16“
Persönliche Werkzeuge