Aus ProgrammingWiki

Inhaltsverzeichnis

1 Berechenbarkeit und Kreativität
2 Definitionen und Beweise
3 Übungen

Berechenbarkeit und Kreativität

Beweise für unendliche Mengen

TODO: Beweismöglichkeiten für abzählbare Mengen (zB.: sortieren, surjektive Abbildungen aufstellen, ...), Widerspruchsbeweise für Abzählbarkeit übersichtlich in einer Grafik darstellen!

abzählbar unendliche Mengen = Menge ist gleichmächtig zu den natürlichen Zahlen

Vorstellungsvermögen: Wenn man als Beispiel eine bijektive Abbildung zählt und bei natürlicher zahl (1 Billion) und der dazugehörigen Zahl der Vergleichsmenge (40) ankommt, dann könnte man erstmal denken, dass Vergleichsmenge weniger mächtig ist, weil 40 kleiner als 1 Billion, aber es geht um die ANZAHL DER ELEMENTE (KARDINALITÄT) BEIDER MENGEN und dahingehend sind beide gleich.

Beweis über eine surjektive Abbildung.

z.B.: Beweis, dass ganze Zahlen (Z) abzählbar unendlich sind:

1 -> 1

2 -> -1

3 -> 2

4 -> -2

5 -> 3

...

Beweis, dass gerade Zahlen (G) abzählbar unendlich sind:

1 -> 2

2 -> 4

3 -> 6

4 -> 8

...

Zudem gilt: G Teilmenge von N

Beweis, dass rationale Zahlen (Q) abzählbar unendlich sind: Sequenz (Reihenfolge) der bijektiven Abbildung zwischen N und Q kann mithilfe von Cantor'sches Diagonalverfahren 1. Art bestimmt werden.

Beweis, dass M1 vereinigt M2 abzählbar unendlich sind, wobei M1 und M2 jeweils abzählbar unendliche Mengen sind:

Möglichkeit 1: Bestimmung der Sequenz der Abbildung über Cantor' Diagonalverfahren 1. Art

Möglichkeit 2:

1 -> M1(1. Element)

2 -> M2(1. Element)

3 -> M1(2. Element)

4 -> M2(2. Element)

5 -> M1(3. Element)

...

Eine weitere Möglichkeit, um eine abzählbar unendliche Menge zu beweisen ist das Sortieren der Elemente (Wörter). Ein mögliches Sortierkriterium wäre bei einer Wortmenge die Länge der einzelnen Wörter. (längenlexikografische Ordnung)

überabzählbar unendliche Mengen:

siehe Cantor'sches Diagonalverfahren 2. Art

Idee dahinter: Man hat eine beliebige Menge an Wörtern. An dieser Menge wird die Hauptdiagonale angelegt. Anschließend wird ein neues Wort erzeugt, indem für (n, a) das Zeichen geändert wird. Die Änderung des Zeichens für das neue Wort muss dabei einer Regel erfolgen, die auf Basis des aktuellen Zeichens ein anderes Zeichen des Alphabets verwendet.

(x, y) : (Zeile, Spalte); n : durchlaufende Zeile; a : Spalte innerhalb der Hauptdiagonale

Beispiel:

A = {a, b}

Regel: wenn a -> b; wenn b -> a

	z1	z2	z3	z4	...
w1	a	b	b	a	...
w2	b	a	a	a	...
w3	a	a	a	a	...
w4	a	a	b	b	...
wn	b	b	b	a	...

z = Zeichen; w = Wort; wn = neues Wort

Auf Basis dessen kann man als Wort auch ein Zahlwort verwenden. Um zu beweisen, dass die reellen Zahlen (R) überabzählbar unendlich sind, wurde dieses Verfahren verwendet. Da von jedem Zahlwort eine Ziffer verändert wird, erhält man ein neues Zahlwort.

FRAGE: Würde man nicht aber auch immer ein unterschiedliches Zahlwort erhalten, wenn man die rationalen Zahlen auf das Cantor'sche 2. Diagonalverfahren anwendet?

Idee: Vielleicht??, aber alle rationalen Zahlen können neben der Dezimalschreibweise auch als p/q dargestellt werden, wobei sowohl p als auch q in p/q natürliche Zahlen sind.

Entscheidbarkeit

Bereich Mengen: Entscheidbarkeit, Bereich Funktionen: Berechenbarkeit

Was ist damit gemeint??

Es wird eine Funktion definiert, welche Berechungen vornimmt und die Ausgabe-Werte aufzählt (also als Menge zurückgibt). Anhand der ausgegebenen Menge kann eine weitere Funktion (=chi-Funktion/charakteristische Funktion) entscheiden, ob ein bestimmtes Element in dieser Menge enthalten ist. Sie nimmt ein Vergleichselement/Vergleichswort w als Parameter auf. Iteriert über jedes Element der Ausgabe-Menge und gibt wahr aus, sobald w in Menge vorkam, ansonsten falsch. Ist die Ausgabe-Menge abzählbar unendlich, kann zum Iterieren der Menge Streams genutzt werden. Das Vergleichswort w kann aus der Wortmenge A* stammen, wenn man jedes mögliche Wort des Alphabets A testen will.

Beispiel:

Berechnungsfunktion: Zähle alle Primzahlen ab der Zahl n auf, gib alle Wörter der Sprache aus, gib alle Personen des Studiengangs n aus, ...

chi-Funktion: Iteriere, ob die Zahl 67 in der Primzahlmenge ab 35 enthalten ist; Iteriere, ob Max Mustermann in der Personenmenge des Studiengangs xyz enthalten ist.

Die ausgegebene Menge der Berechnungsfunktion heißt auch aufzählbar, da die Menge abzählbar und die Funktion zu dieser Menge berechenbar sein muss.

Frage: Wieso kann man mithilfe dieser charakteristischen Funktion für eine abzählbar unendliche Menge entscheiden, ob ein Element (Wort) innerhalb dieser Menge nicht vorkommt? (also die chi-Funktion false zurückgibt?)

Antwort: Weil man bei einer abzählbar unendlichen Menge die Elemente (Wörter) sortieren kann (z.B.: längenlexikografisch). Beispiel: Wenn die Menge absteigend nach Länge der Wörter sortiert sind und es in der Menge kein Wort mit der selben Länge des Vergleichsworts gibt, kann false ausgegeben werden.

semi-entscheidbare Menge: Diese charakteristische Funktion ist ähnlich zu der für entscheidbare Mengen mit dem Unterschied, dass die Funktion weiterläuft, wenn das Vergleichselement nicht gefunden wurde anstatt dass false ausgegeben wird.

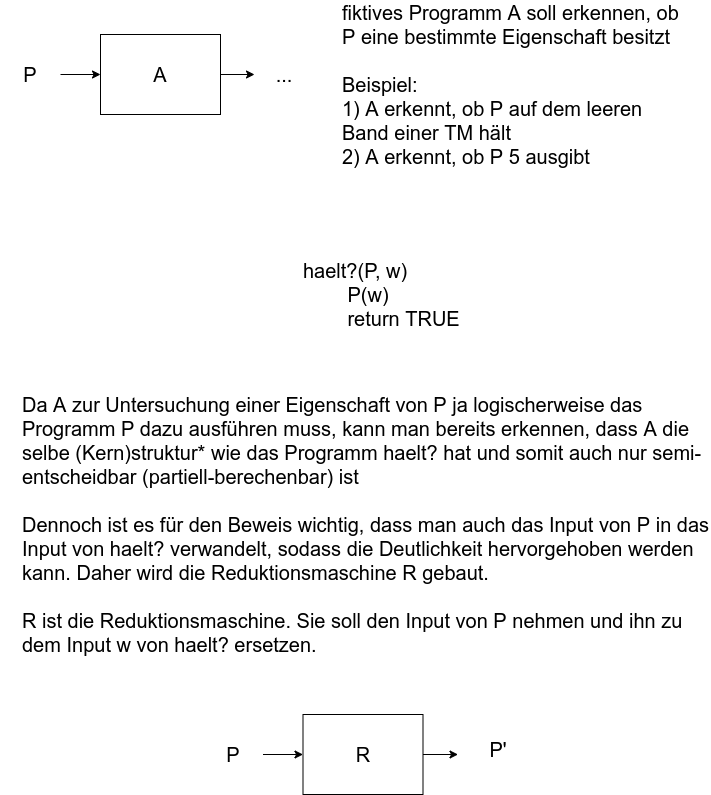
Beweis, dass Halteproblem semi-entscheidbar ist:

def haelt(prog, param): prog(param) return True def endless(n): endless(n) def fak(n): if n == 0: return 1 return n * fak(n - 1)

print(haelt(fak, 3))

print(haelt(endless, 0))

Ansatz: Fibonacci-Zahlwörter deswegen entscheidbar, weil sortierbar

ÜA: Die Menge G der Gitterpunkte (0, 0),(0, 1), . . . einer x-y-Ebene ist aufzählbar.

bijektive Abbildung f von N auf G mithilfe von Cantor'schem Diagonalisierungsverfahren 1. Art als Sortierverfahren: (beweist Abzählbarkeit von G und G lässt sich auch aufzählen)

1 -> (0,0)

2 -> (0,1)

3 -> (1,0)

4 -> (2,0)

5 -> (1,1)

6 -> (0,2)

...

Ordnungsrelation:

def kleiner(a: tuple, b: tuple): suma = a[0] + a[1] sumb = b[0] + b[1] return suma < sumb

Indexfunktion i(x, y) bildet (x,y) von G bijektiv auf N ab. (Beispiel: i((0,2)) -> 6)

Beweise für (Ab/Auf)-zählbarkeit, (Semi)entscheidbarkeit

Satz 1: Eine Menge M ist genau dann aufzählbar, wenn sie semi-entscheidbar ist.

Teil 1: M aufzählbar -> M semi-entscheidbar

Wir wissen, dass wir eine aufzählbare Menge M haben und wollen herausfinden, ob wir daraus eine chi-strich-Funktion erzeugen können

da für M keine "festgeschriebene" Menge vorhanden ist, sondern nur Aufzählfunktion f, kann f(0), f(1), ... anstelle für M in chi-strich-Funktion verwendet werden

Teil 2: M semi-entscheidbar -> M aufzählbar

Wir wissen, dass wir eine chi-strich-Funktion haben und wollen wissen, ob wir daraus eine aufzählbare Menge M erzeugen können. Man will also die Ausgabe von chi-strich verwenden, um zu wissen, ob ein Element von w aus A* zu M gehört.

Wenn wir statt chi-Strich eine chi-Funktion hätten, könnten wir jedes Wort w aus der Wortmenge A* in die chi-Funktion als Parameter eingeben und im Falle einer TRUE-Ausgabe das Wort w in die Menge M hinzufügen und bei einem FALSE dieses Wort w ignorieren.

Bei chi-Strich ist es schwieriger, da anstelle von FALSE chi-strich hält.

Möglichkeit nach Vorlesungsfolie: Erstellen einer Paarungsfunktion (x = Elementnummer x aus A*, y = Abbruch nach Zeit y), welche für jedes (x, y) die Ausgabe z einzigartig codiert.

TODO: Herleitung (x und y aus z) nochmal anschauen und verinnerlichen

FRAGE: Alternative Möglichkeit: Anstelle von Paarungsfunktion wird eine Paar-Tabelle aufgestellt (Key = Wort aus A*, Value = Abbruch nach Zeit <Value>). Sobald ein Wort w aus A* in mit chi-Strich getestet wird, wird für dieses w aus der Paar-Tabelle die Zeit entnommen. Die Aufzählfunktion f nimmt also ein Wort w aus A* entgegen, entnimmt für w die Zeit aus der Tabelle und testet bis zu dieser Zeit. Wenn bis zu dieser Zeit TRUE ausgegeben wird, wird w in die Menge M aufgelistet???

Satz 2:

Jede Teilmenge einer (beliebigen) abzählbaren Menge ist abzählbar, aber

FALSCH ist: Jede Teilmenge einer (beliebigen) aufzählbaren Menge ist aufzählbar.

Teil 1: M Teilmenge von M2; M2 abzählbar; M abzählbar?

Im Grunde ist "M Teilmenge von M2" schon der Beweis, weil wenn M2 abzählbar ist, dann ist die Teilmenge M auch abzählbar.

Wenn es zwischen N und M2 mindestens eine Surjektion gibt, dann gibt es diese auch zwischen N und M. (siehe Mengenbild auf Vorlesungsfolie 4 S. 23)

Teil 2: M Teilmenge von M2; M2 aufzählbar; M aufzählbar?

Es existiert eine Aufzählfunktion f2. M2 allerdings nur semi-entscheidbar, da M2 keine Ordnung haben muss. Hinweis: Abzählbar bedeutet nur, dass Bijektion zwischen N und der jeweiligen Menge vorhanden sein muss, nicht dass eine Ordnung existiert.

Man kann M doch als Teilmenge generieren lassen und dann Aufzählfunktion??? Antwort: Ja, aber die Anzahl dieser generierten Teilmengen entspricht nicht JEDER Teilmenge, wie im Satz gefordert. Die Teilmenge kann auch zufällig sein.

Für den Beweis kann eine Aufzählfunktion f nicht mittels Parameter start und ende eingegrenzt werden, da von endlichen nicht auf unendliche Mengen schließbar ist.

Frage für 26.4.:Anstelle von start/ende wird in f eine Rechenvorschrift gewählt. Beispiel: f(gerade Zahlen aus M2) als Funktion, um Teilmenge zu generieren

Frage für 26.4.:Zur Folie S. 25: Charakteristische Funktion chi muss nicht berechenbar sein, damit diese als Hilfe verwendet werden kann, um Teilmenge aufzuzählen. Es müsste auch semi-charakteristische Funktion ausreichen (siehe Satz 1: Teil 2)

Frage für 26.4.:Wie kann man wissen, ob zB dieser Beweis gültig ist? (va., wenn kein Logikfehler erkennbar ist?)

Satz 3: Wenn die Menge M entscheidbar ist, dann ist M aufzählbar. Die Umkehrung dieses Satzes gilt nicht!

Teil 1: M entscheidbar -> M aufzählbar?

chi-Funktion für M existiert

FRAGE für 26.4: Frage nach Abzählbarkeit wichtig? Ist M abzählbar (gibt es für M eine Surjektion zwischen N und M/ist M sortierbar)? M ist abzählbar, da chi nur mit abzählbaren Mengen arbeiten kann.

Warum kann chi nur mit abzählbaren Mengen arbeiten? Da man bei überabzählbar unendlichen Mengen nicht wissen kann, ob w aus A* auch in M enthalten ist. Bei abzählbar unendlichen Mengen kann man mithilfe einer Ordnung/Sortierung u.a. darüber entscheiden, dass w nicht mehr in M vorkommen kann.

Gibt es eine Aufzählfunktion f für Menge M? Da es eine charakteristische (Chi)-Funktion im Verhältnis zur bildbaren Wortmenge A* gibt, gibt es eine Aufzählfunktion f. Man kann also jedes Wort w von A* in chi eingeben und sobald WAHR rauskommt, wird w in die Menge M hinzugefügt.

Teil 2: M aufzählbar -> M entscheidbar?

Nein, da aufzählbare Menge M nicht unbedingt eine Ordnung haben muss -> nur semi-entscheidbar

Satz 4: Eine Menge M aus A* ist entscheidbar genau dann, wenn M und A* \ M (Komplementmenge) aufzählbare Mengen sind.

Teil 1: M entscheidbar -> M und A* \ M aufzählbar

Es existiert eine chi-Funktion für M.

Zur Aufzählbarkeit:

Frage für 26.4.:Ist Frage nach Abzählbarkeit nötig?</b>Ist M abzählbar? M ist abzählbar, da chi nur mit abzählbaren Mengen arbeiten kann.

Hat M eine Aufzählfunktion f? Da es eine charakteristische (Chi)-Funktion im Verhältnis zur bildbaren Wortmenge A* gibt, gibt es eine Aufzählfunktion f. Man kann also jedes Wort w von A* in chi eingeben und sobald WAHR rauskommt, wird w in die Menge M hinzugefügt.

Ist A* \ M abzählbar? Ja, da die Wortmenge A* längenlexikografisch geordnet werden kann und M auch abzählbar ist, wodurch die Komplementmenge gebildet werden kann.

Hat A* \ M eine Aufzählfunktion g? Ja, da die Wortmenge A* längenlexikografisch geordnet berechnet werden kann und da M aufzählbar ist, ist auch das Komplement A* \ M aufzählbar.

Teil 2:

Wenn M und A* \ M aufzählbare Mengen sind, dann ist M eine entscheidbare Menge.

M ist abzählbar (es existiert eine surjektive Abbildung zwischen N und M)

Es existiert eine Aufzählfunktion für M.

A* \ M ist abzählbar (es existiert eine surjektive Abbildung zwischen N und M)

Es existiert eine Aufzählfunktion für A* \ M.

Existiert eine Chi-Funktion für M? Ja, siehe Seite 30 (hier vielleicht leicht abgewandelt)

Es gibt nur zwei Mengen und beide davon sind bekannt. Einmal die Wortmenge A* und einmal die Teilmenge M aus A*. Die Wortmenge A* ist längenlexikografisch geordnet und damit abzählbar und entscheidbar. Die Wortmenge A* enthält alle möglichen Wörter. Ist das zu untersuchende Wort w nicht in A* enthalten, kann es nur in M enthalten sein.

Alternativbeweis für Nichtexistenz eines Totalmachers tm:

Folgendermaßen könnte man tm konstruieren:

1.) Aufstellen des Halteprogramms haelt?

def haelt(prog, param): prog(param) return True

2.) beispielhafte partielle Funktion fp aufstellen:

def fp(n): if n == 3: fp(n) return n

Nun könnte man den Totalmacher tm bauen, der jedes Argument n von fp durchgeht. Dabei gibt es schonmal Problem 1, weil man jedes Argument n (Unendlichkeit) durchgehen müsste.

Problem 2 wäre, dass selbst ohne Problem 1 man für die hier angegebene Definitionslücke n = 3 nur entscheiden könnte, ob fp für dieses n hält und nicht, ob fp für dieses n nicht hält.

Dieses Problem hätte man allerdings mit Zeitscheiben (siehe Satz 1 Teil 2) beweisen können.

Satz von Rice

TODO: Bild hochladen

Inspiration: https://www.youtube.com/watch?v=PCFyC-bNTvk

Gödelisierung

Aufbau einer Gödelisierungsfunktion sowie seiner inversen Funktion mithilfe von Primfaktorzerlegung

A = ['a', 'b'] codes = { A[0] : 1, A[1] : 2 } def G(w): res = 1 prims = genPrims(len(w)) for i in range(0, len(prims)): fact = prims[i] ** codes[w[i]] res = res * fact return res #TODO: ACHTUNG: BISHER NUR SEMI-ENTSCHEIDBAR. MUSS ALSO FUNKTION GEBEN, UM ZU ERMITTELN, OB NUMMER N SCHON ZU KLEIN FÜR EINE BESTIMMTE WORTLÄNGE IST def invG(n): l = 1 while True: aStar = genAstarByLength(l) for w in aStar: if G(w) == n: return w l = l + 1 def genPrims(n): res = [] i = 2 while len(res) < n: isPrime = True for j in range(2, i): if i % j == 0: isPrime = False if isPrime: res.append(i) i = i + 1 return res def genAstarByLength(length): return _genAstarByLength(length, [], []) def _genAstarByLength(length, word, res): if length == 0: res.append(word.copy()) return res for i in A: word.append(i) _genAstarByLength(length - 1, word, res) word.pop() return res

print(G(['a'])) print(invG(90)) #print(invG(98)) # SIEHE ZEILE 20!!!

HINWEIS: Die Gödelisierung betrifft - wie an G und invG auch erkennbar - nur die Syntax und nicht die Semantik

FRAGE FÜR 17.5.: Seite 21: Wieso wird Mfa = Mphi gleichgesetzt?

Widerspruchsbeweis zur Entscheidbarkeit des Halteproblems

stop = True def M(P, E): return stop def Mstrich(U): if M(U, U): Mstrich(U) return True print(Mstrich(Mstrich)) #def M(P, e): # P(e) # return True

Die Funktion M stellt die Annahme für den Widerspruch dar, dass es eine total-berechenbare Funktion für das HP gibt. Da wir allerdings wissen, dass es diese nicht gibt, muss hier mit einer "Pseudo-Funktion" gearbeitet werden, wo "stop" manuell einstellbar ist.

Sollte M sagen, dass P mit E stoppt, dann geht Mstrich in eine Endlosschleife über. Ansonsten wird True ausgegeben.

Mstrich wird mit Mstrich aufgerufen.

Der Widerspruch besteht jetzt darin, dass im Falle dass M(Mstrich, Mstrich) = False ist, Mstrich = True ist. Sollte M(Mstrich, Mstrich) = True sein, bringt Mstrich keinen Widerspruch, da es in eine Endlosschleife geht. Würde Mstrich für diese Situation dagegen False ausgeben, wäre es ein Widerspruch.

Unten im Code auskommentiert befindet sich noch eine alternative Funktion M, welche das partiell-berechenbare HP darstellt, welches ja existiert. Wenn Mstrich(Mstrich) mithilfe dieses M verarbeitet wird, kann es nur in die Endlosschleife gehen. (=also kein Widerspruch). True (also den Widerspruch) würde Mstrich hier nie ausgeben können. Daher würde man bei Verwendung des existierenden partiell-berechenbaren HP hier nicht in den Widerspruch gelangen.

Hier gefragt: https://matheplanet.com/matheplanet/nuke/html/viewtopic.php?topic=258897

Anbei habe ich noch eine Überlegung gestartet, wenn wir ein HP konstruieren, das bis zu einer bestimmten Laufzeit (10sec) von P wartet und True ausgibt (also es hält) und sollte es länger dauern, wird False ausgegeben. Das ist natürlich eine falsche Überlegung, aber interessant, wenn man dies mit dem Widerspruchsbeweis testet. Sollte länger als 10sec gewartet worden sein, wird für M = False ausgegeben und somit für Mstrich = True ausgegeben (=Widerspruch)

def M(P, E): if lessThen10sec(P(E)): return True return False

Weitere Berechnungsmodelle und deren Mächtigkeit

Jedes LOOP-Programm ist Turing-berechenbar. (Beweis mithilfe von RAM)

1:R1:=n Element N 2:A1 ... n:An n Anweisungen 4:DEC(R1) 5:GOTO_IF_HIGHER(R1,0,2) 6:STOP

Jedes WHILE-Programm ist Turing-berechenbar. (Beweis mithilfe von RAM)

1:R1:=1 2:A1 ... n:An n Anweisungen (R1:=0 ist mögliche Anweisung) 5:GOTO_IF_EQUALS(R1,1,2) 6:STOP

Für umgedrehte Beweise siehe Vorlesungsfolie

Definitionen und Beweise

aufzählbar: abzählbar (FRAGE für 26.4: nur auf Wortmenge A* bezogen???) und berechenbar (vielleicht kleiner Denkfehler: abzählbar bedeutet ja nicht nur, dass es Menge sortierbar sein muss, aber nicht nur bei Wortmenge A* gibt es Sortierung, auch bei ganzen Zahlen, rationalen Zahlen gab es ja eine Sequenz = Sortierung)

abzählbar: Surjektion zwischen N und M vorhanden

berechenbar: es existiert Funktion f, die zu M führt (muss NICHT terminieren)

effektiv-berechenbar: es muss kein Programm vorliegen, sondern es muss nur ein Verfahren vorliegen

semi-entscheidbar: es existiert chi-strich-Funktion

entscheidbar: es existiert eine chi-Funktion

partiell-berechenbar = semi-entscheidbar

Warum folgt aus der Aufzählbarkeit einer Menge M nicht die Entscheidbarkeit, sondern nur die Semi-Entscheidbarkeit? Weil eine Menge M keiner Ordnung/Sortierung folgen muss.

BuK/IIm21/Lambda-Kalkül Reduktionsregeln

BuK/IIm21/LOOP, WHILE, GOTO Umwandlungen