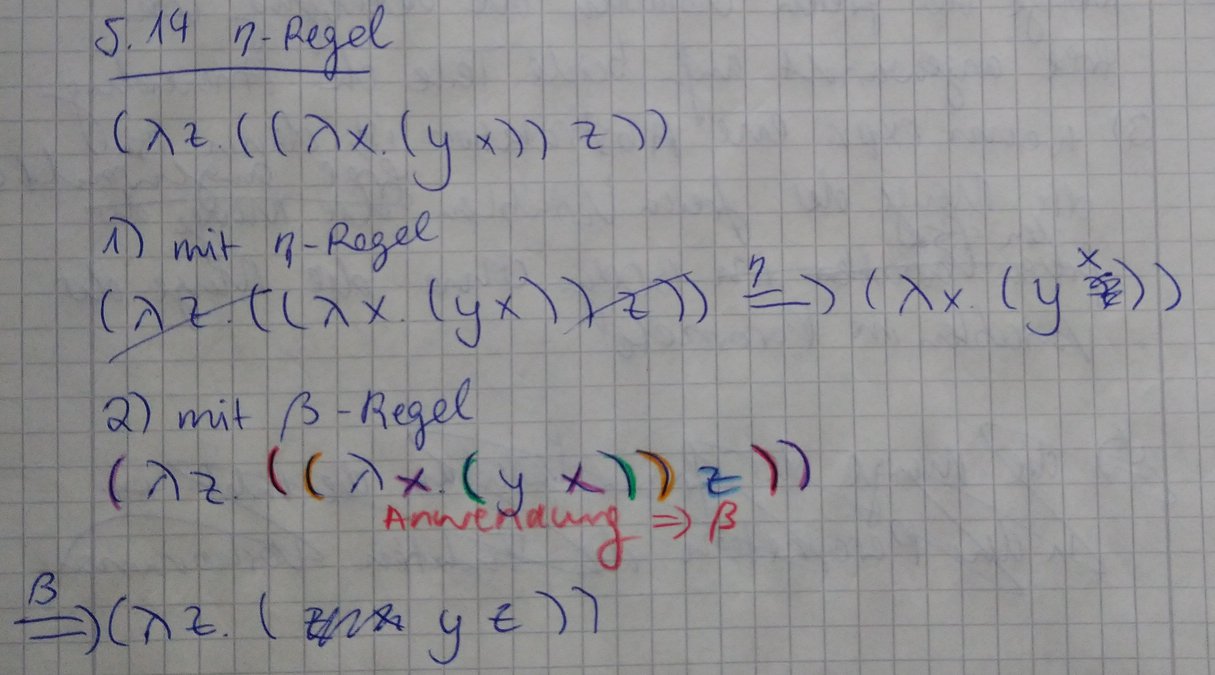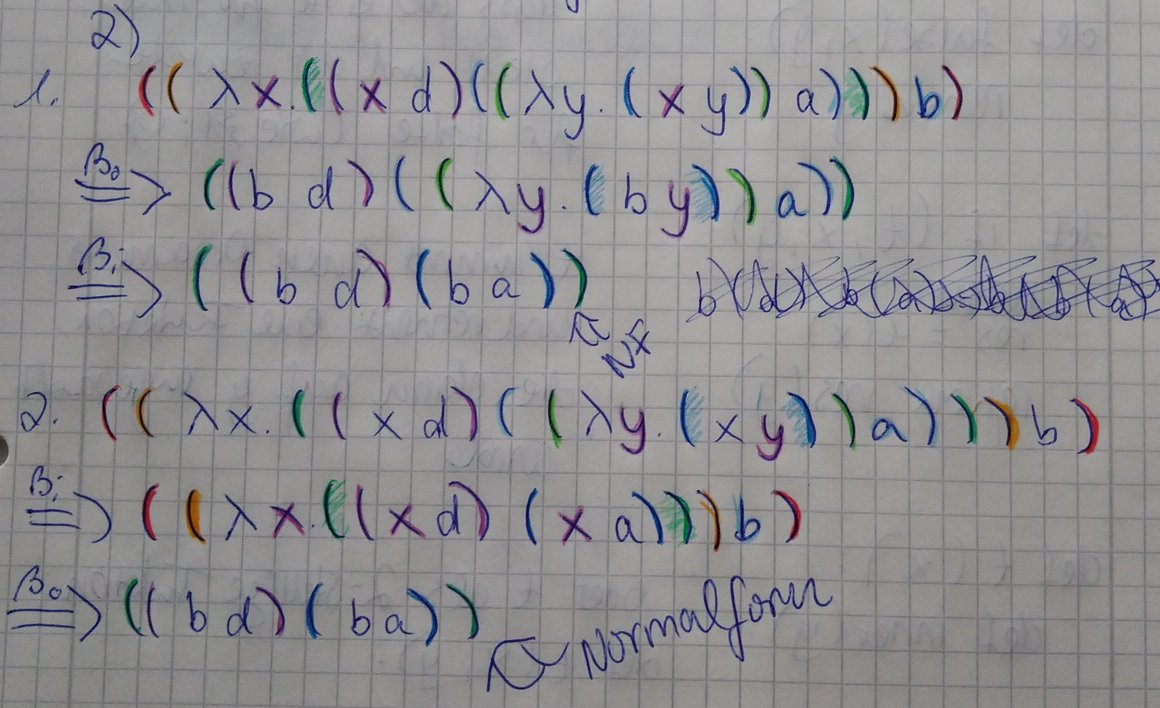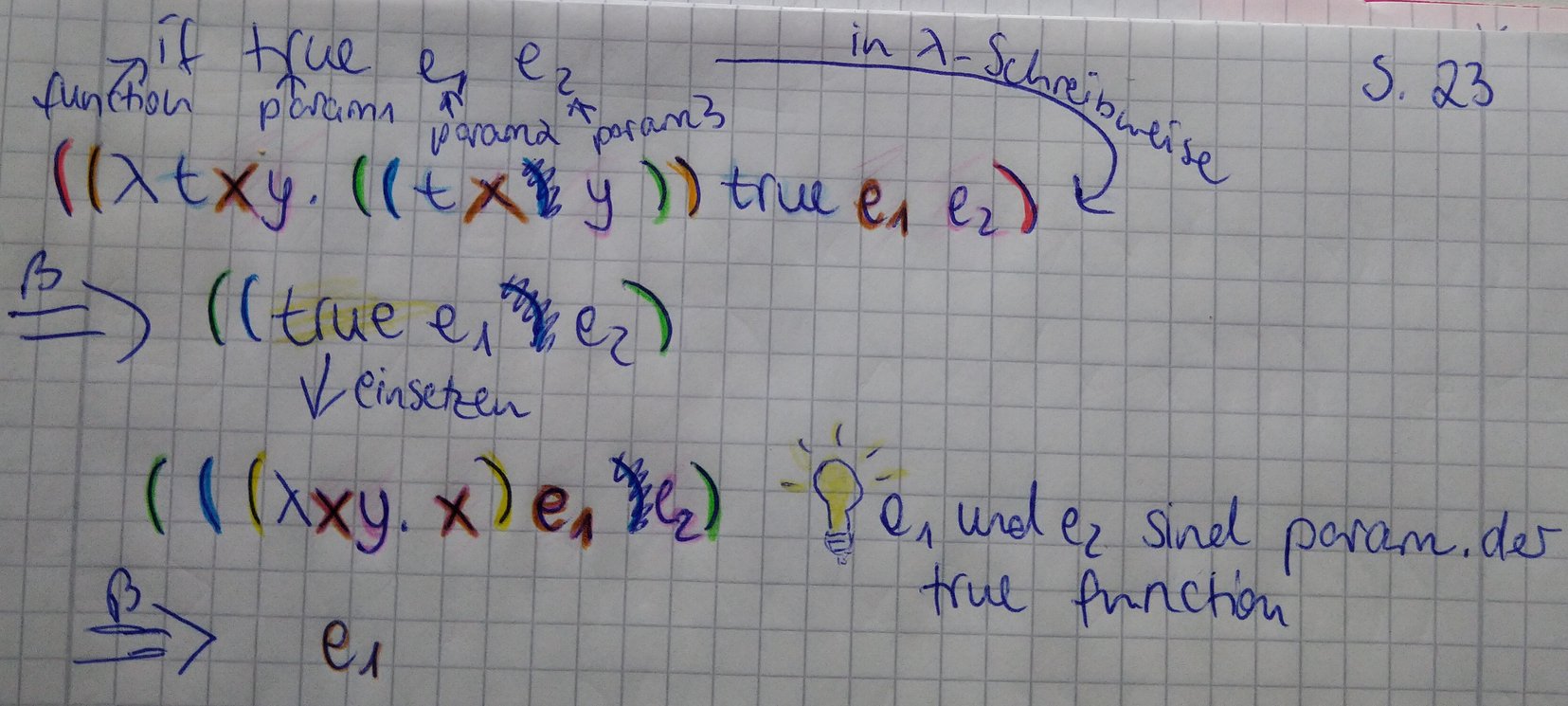Vorlesung 9 Lemke
Aus ProgrammingWiki
Inhaltsverzeichnis |
Übungsaufgabe S. 5
Implementation der angegebenen Lambdafunktionen in Python
(λx. x)
(λf . (λx. (f x) ) )
Als Python-Lambdafunktion:
Als reguläre Pythonfunktion:
Übungsaufgabe S. 11
Erklärung der Funktion free() (bound() funktioniert analog)
Übungsaufgabe S. 13
Anwendung der ɑ-Konvention
Übungsaufgabe S. 14
Reduktion mit η-Regel und mit β-Regel
Übungsaufgaben S. 15
Reduzieren Sie ((λ(x)(x x))(λ(x) x)) und ((λ(x)(x x))(λ(x)(x x)))
Zeigen Sie, dass für Y := (λf . ((λx. (f (x x)))(λx. (f (x x))))) gilt: (Y g ) = (g (Y g ))
Übungsaufgabe S. 17
Zeigen Sie, dass es von der Reduktionsreihenfolge abhängen kann, ob die für ((λy . z)((λx. (x x))(λx. (x x)))) existierende Normalform z gefunden wird oder nicht
Verwenden Sie zur Berechnung von ((λx. ((x d)((λy . (x y )) a))) b) unterschiedliche Reduktionsreihenfolgen
Übungsaufgabe S. 22
Currifizieren Sie f (x, y , z) = x + y + z
Mit Python-Lambdafunktionen:
Mit regulären Pythonfunktionen: