Vorlesung 8 Seidl

Aus ProgrammingWiki

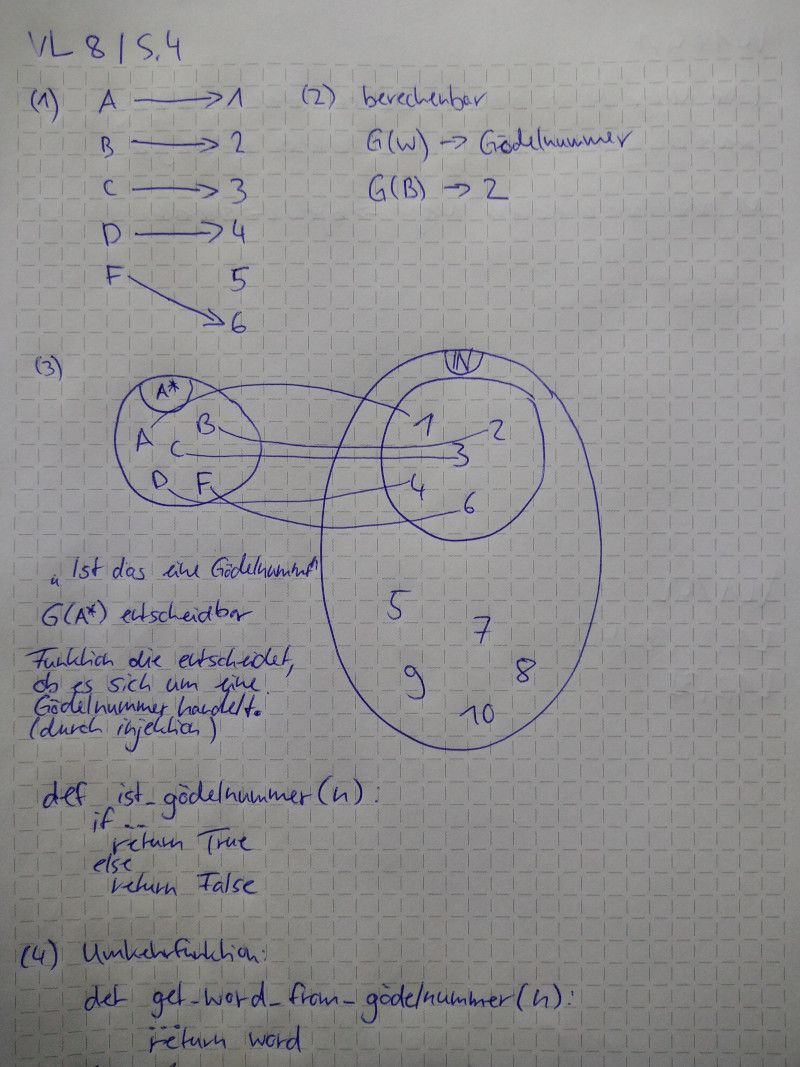
S. 4

S. 11

import itertools # A Generator alphabet = ["a", "b", "c"] def a(alphabet): for i in range(0, len(alphabet)+1): for word in itertools.product(alphabet, repeat=i): yield word def wort_index(buchstabe, wort): for i, w in enumerate(a(wort)): if len(w) != 1: continue if w[0] == buchstabe: return i # Primzahl Generator def primzahl_generator(n): while True: if ist_primzahl(n): yield n n += 1 def ist_primzahl(n): if n == 2: return True for i in range(2, n): if n % i == 0: return False return True # Gödelnummer def get_goedelnummer(wort): elemente = [] for i_b, buchstabe in enumerate(wort): primzahl = -1 for i_p, p in enumerate(primzahl_generator(2)): primzahl = p if i_b == i_p: break xi = wort_index(buchstabe, wort) elemente.append(primzahl**xi) produkt = 1 for faktor in elemente: produkt = faktor * produkt return produkt # Reverse Gödelnummer (Holzhammer) def wort_von_goedelnummer(n): for w in a(alphabet): goedelnummer = get_goedelnummer("".join(w)) if goedelnummer == n: return "".join(w)

print(get_goedelnummer("aba")) print(wort_von_goedelnummer(90))

ausführen

S. 13

Satz: f ist eine berechenbare Funktion genau dann, wenn h eine berechenbare Funktion ist.

Ausschroten:
kurz: h = G^−1 ◦ f ◦ G
ausgeschrieben: h = G^−1(f(G(w)))

G(w) gibt uns für ein Wort w die zugehörige Gödelnummer i
f(i) gibt uns für die Gödelnummer i des Wort w eine übertragene Gödelnummer j, welche auch die Gödelnummer des Wortes w' ist
G^-1(j) gibt uns das Wort w' aus der Gödelnummer von eben dieser (j)

kurz: f = G ◦ h ◦ G^−1
ausgeschrieben: f = G(h(G^-1(w'))

G^-1(w') gibt uns für ein Wort w' die zugehörige Gödelnummer j
h(j) gibt uns für die Gödelnummer j des Wort w' eine übertragene Gödelnummer i, welche auch die Gödelnummer des Wortes w ist
G(i) gibt uns das Wort w aus der Gödelnummer von eben dieser (i)

Bijunktion, <->

Versuch eines argumentativen Beweises:

Aus den Eigenschaften (VL 8, S. 4) der Gödelisierung geht hervor, dass G und G^-1 berechenbare Funktionen sind. Fraglich ist somit nur noch, ob f auch berechenbar ist. Bedingung dabei ist, dass f berechenbar ist, genau dann wenn h es auch ist. Mittels h können wir das Wort w' aus dem Wort w ermitteln. Dies ist sozusagen der kurze Berechnungsweg. Der lange Weg über die Gödelisierung geht mittels Funktion G und beinhaltet auch die Funktion f. Wenn wir also das Wort w' aus Wort w berechnen können, so ist auch Funktion f berechenbar, welche uns für die Gödelnummer des Wortes w die Gödelnummer des Wortes w' berechnet.